数学人教版八年级下册18.2.3第5课时 正方形教学课件(共16张ppt)
文档属性
| 名称 | 数学人教版八年级下册18.2.3第5课时 正方形教学课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 786.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 15:42:57 | ||
图片预览


文档简介
(共16张PPT)
第18章 平行四边形
第5课时 正方形
18.2 特殊的平行四边形
学习目标
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别,进一步体会特殊与一般的关系.
课堂导入
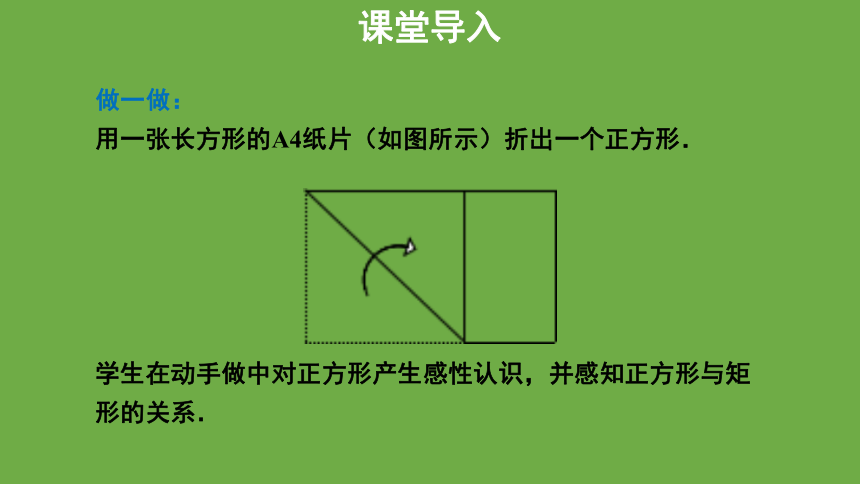
做一做:
用一张长方形的A4纸片(如图所示)折出一个正方形.
学生在动手做中对正方形产生感性认识,并感知正方形与矩形的关系.
新知讲解
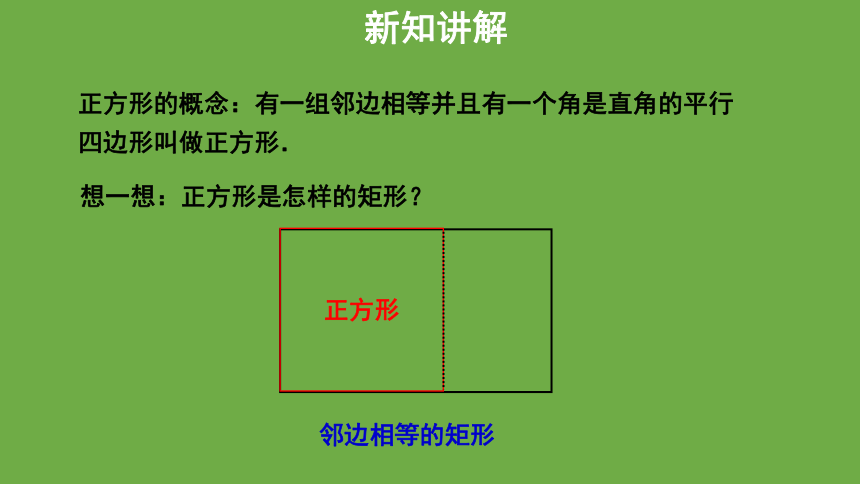
正方形的概念:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形
邻边相等的矩形
想一想:正方形是怎样的矩形?
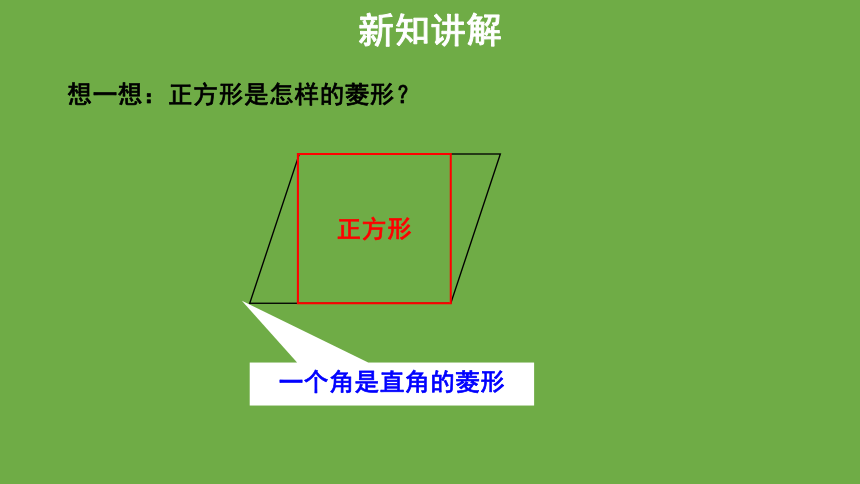
一个角是直角的菱形
想一想:正方形是怎样的菱形?
正方形
新知讲解
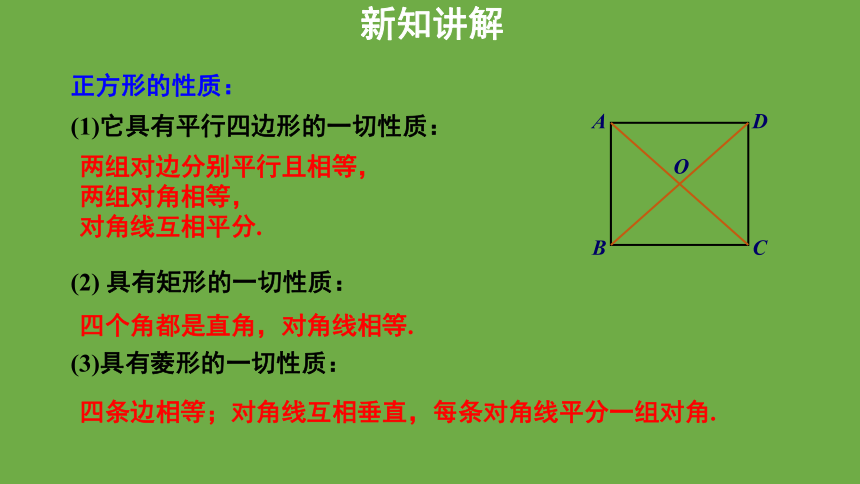
(1)它具有平行四边形的一切性质:
两组对边分别平行且相等,
两组对角相等,
对角线互相平分.
(2) 具有矩形的一切性质:
四个角都是直角,对角线相等.
(3)具有菱形的一切性质:
四条边相等;对角线互相垂直,每条对角线平分一组对角.
O
A
B
C
D
正方形的性质:
新知讲解
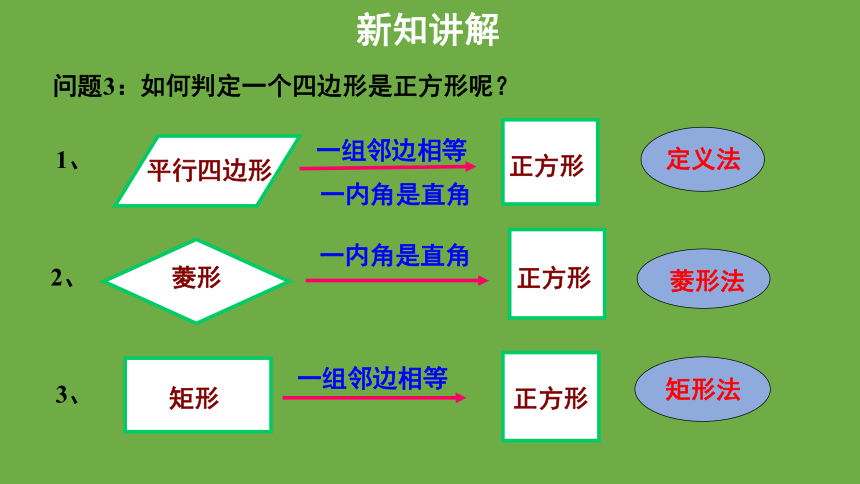
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
问题3:如何判定一个四边形是正方形呢?
菱形法
矩形
3、
一组邻边相等
正方形
矩形法
定义法
新知讲解
新知讲解
问题4:平行四边形和矩形、菱形、正方形之间的关系是什么?
四边形
平行四边形集合
菱形
矩形
正方形
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
O
A
B
C
D
已知,如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
典型例题
典型例题
证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.
O
A
B
C
D
例2 如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN
证明:
A
B
C
D
P
M
N
连接PC.
∵PM⊥BC , PN⊥DC,四边形ABCD是正方形,
∴∠PMC=90°, ∠PNC=90°, ∠NCM=90°.
∴四边形PMCN是矩形.
∴PC=MN.
又四边形BAPC关于BD成轴对称,
∴AP=PC,
∴AP=MN.
典型例题
1、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.
解:∵四边形ABCD是正方形,
∴AC平分∠BCD, ∠BCD= ∠DCE=90°.
∴ ∠ACB=45°.
∵CE=AC, ∠CAE+ ∠E= ∠ACB,
∴ ∠E=22.5°,
∴ ∠AFC= ∠DCE+ ∠E=90°+22.5°=112.5°.
A
B
D
C
E
F
随堂练习
2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥BC.求证:四边形CEDF是正方形.
A
B
C
D
E
F
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
∴DE=DF.
∵ CD平分∠ACB,DE⊥AC, DF⊥BC,
∴ 四边形CEDF为矩形.
又∠ACB=90°,
∴ ∠DEC=90°, ∠DFC=90°
证明:
∵ DE⊥AC,DF⊥BC,
随堂练习
3、四边形ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?
A
D
解:连接AC.∵ 四边形ABCD是正方形,
∴ ∠B=90°,AB=BC.
∵ EC=50m,EB=30m,
∴ S正方形ABCD=40 2=1600(m2),
B
C
E
随堂练习
正方形的性质:
1. 正方形的四条边都相等. 2. 正方形的四个角都相等. 3. 正方形的对角线互相垂直平分且相等,且每一条对角线平分一组对角.
O
A
B
C
D
正方形的定义:一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
课堂小结
正方形的判定:
1.定义法. 2.有一组邻边相等的矩形是正方形.
3.有一个角是直角的菱形是正方形
再见
第18章 平行四边形
第5课时 正方形
18.2 特殊的平行四边形
学习目标
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别,进一步体会特殊与一般的关系.
课堂导入
做一做:
用一张长方形的A4纸片(如图所示)折出一个正方形.
学生在动手做中对正方形产生感性认识,并感知正方形与矩形的关系.
新知讲解
正方形的概念:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形
邻边相等的矩形
想一想:正方形是怎样的矩形?
一个角是直角的菱形
想一想:正方形是怎样的菱形?
正方形
新知讲解
(1)它具有平行四边形的一切性质:
两组对边分别平行且相等,
两组对角相等,
对角线互相平分.
(2) 具有矩形的一切性质:
四个角都是直角,对角线相等.
(3)具有菱形的一切性质:
四条边相等;对角线互相垂直,每条对角线平分一组对角.
O
A
B
C
D
正方形的性质:
新知讲解
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
问题3:如何判定一个四边形是正方形呢?
菱形法
矩形
3、
一组邻边相等
正方形
矩形法
定义法
新知讲解
新知讲解
问题4:平行四边形和矩形、菱形、正方形之间的关系是什么?
四边形
平行四边形集合
菱形
矩形
正方形
例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
O
A
B
C
D
已知,如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
典型例题
典型例题
证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.
O
A
B
C
D
例2 如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN
证明:
A
B
C
D
P
M
N
连接PC.
∵PM⊥BC , PN⊥DC,四边形ABCD是正方形,
∴∠PMC=90°, ∠PNC=90°, ∠NCM=90°.
∴四边形PMCN是矩形.
∴PC=MN.
又四边形BAPC关于BD成轴对称,
∴AP=PC,
∴AP=MN.
典型例题
1、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.
解:∵四边形ABCD是正方形,
∴AC平分∠BCD, ∠BCD= ∠DCE=90°.
∴ ∠ACB=45°.
∵CE=AC, ∠CAE+ ∠E= ∠ACB,
∴ ∠E=22.5°,
∴ ∠AFC= ∠DCE+ ∠E=90°+22.5°=112.5°.
A
B
D
C
E
F
随堂练习
2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥BC.求证:四边形CEDF是正方形.
A
B
C
D
E
F
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
∴DE=DF.
∵ CD平分∠ACB,DE⊥AC, DF⊥BC,
∴ 四边形CEDF为矩形.
又∠ACB=90°,
∴ ∠DEC=90°, ∠DFC=90°
证明:
∵ DE⊥AC,DF⊥BC,
随堂练习
3、四边形ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?
A
D
解:连接AC.∵ 四边形ABCD是正方形,
∴ ∠B=90°,AB=BC.
∵ EC=50m,EB=30m,
∴ S正方形ABCD=40 2=1600(m2),
B
C
E
随堂练习
正方形的性质:
1. 正方形的四条边都相等. 2. 正方形的四个角都相等. 3. 正方形的对角线互相垂直平分且相等,且每一条对角线平分一组对角.
O
A
B
C
D
正方形的定义:一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
课堂小结
正方形的判定:
1.定义法. 2.有一组邻边相等的矩形是正方形.
3.有一个角是直角的菱形是正方形
再见
