2014-2015学年点拨高中数学必修3(北师大版)过关测试卷:第二章+算法初步+过关测试卷
文档属性
| 名称 | 2014-2015学年点拨高中数学必修3(北师大版)过关测试卷:第二章+算法初步+过关测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-03 22:27:37 | ||
图片预览


文档简介
第二章过关测试卷?
(100分,45分钟)
一、选择题(每题5分,共30分)
1.〈北京期末考〉如果输入2,那么执行下面算法的结果是( )
第一步:输入n
第二步:n=n+1
第三步:n=n+1
第四步:输出n
A.输出2 B.输出3
C.输出4 D.程序出错,输不出任何结果
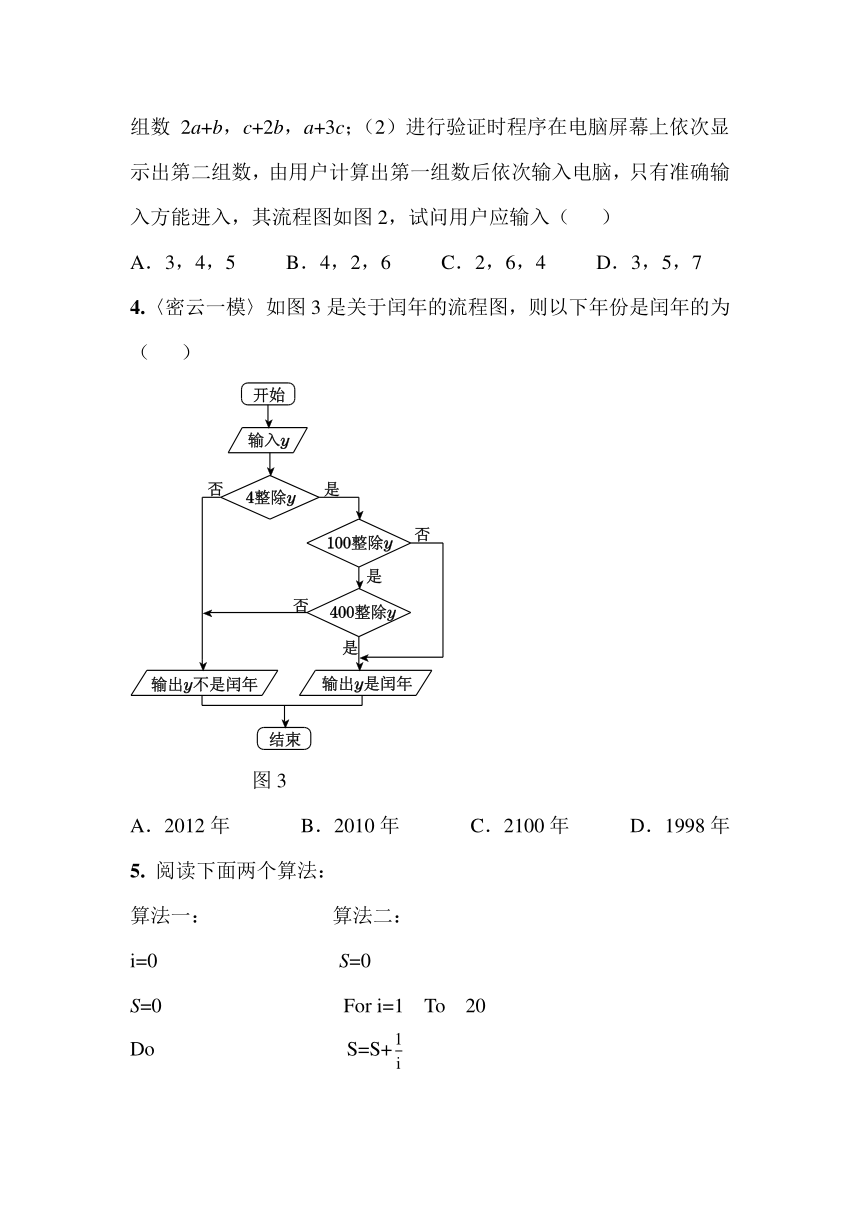
2.〈福州模拟〉执行如图1所示的程序框图后,若输出结果为-1,则输入x的值不可能是( )
A.2 B.1 C.-1 D.-2
图1 图2
3.〈茂名二模〉某银行开发出一套网银验证程序,验证规则如下:(1)有两组数,这两组数存在一种对应关系:第一组数a,b,c对应第二组数2a+b,c+2b,a+3c;(2)进行验证时程序在电脑屏幕上依次显示出第二组数,由用户计算出第一组数后依次输入电脑,只有准确输入方能进入,其流程图如图2,试问用户应输入( )
A.3,4,5 B.4,2,6 C.2,6,4 D.3,5,7
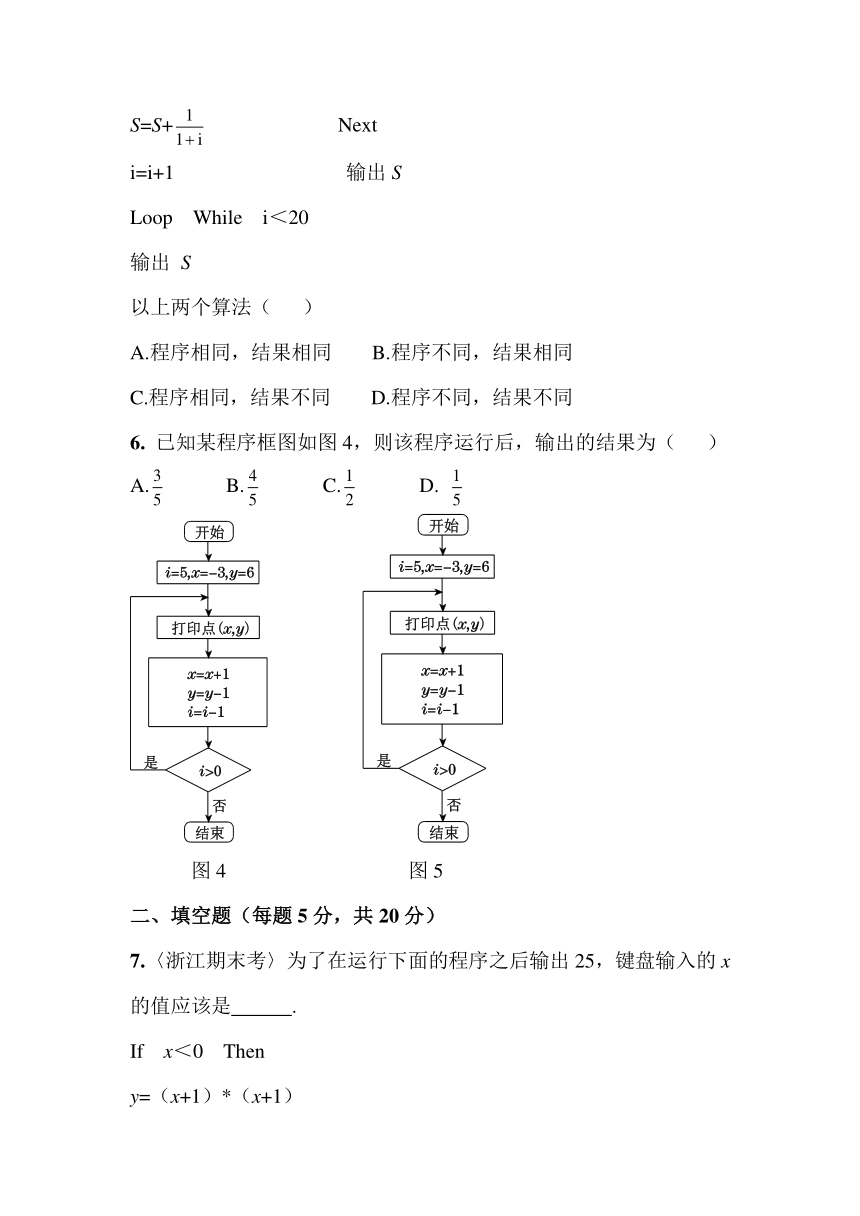
4.〈密云一模〉如图3是关于闰年的流程图,则以下年份是闰年的为( )
图3
A.2012年 B.2010年 C.2100年 D.1998年
5. 阅读下面两个算法:
算法一: 算法二:
i=0 S=0
S=0 For i=1 To 20
Do S=S+
S=S+ Next
i=i+1 输出S
Loop While i<20
输出 S
以上两个算法( )
A.程序相同,结果相同 B.程序不同,结果相同
C.程序相同,结果不同 D.程序不同,结果不同
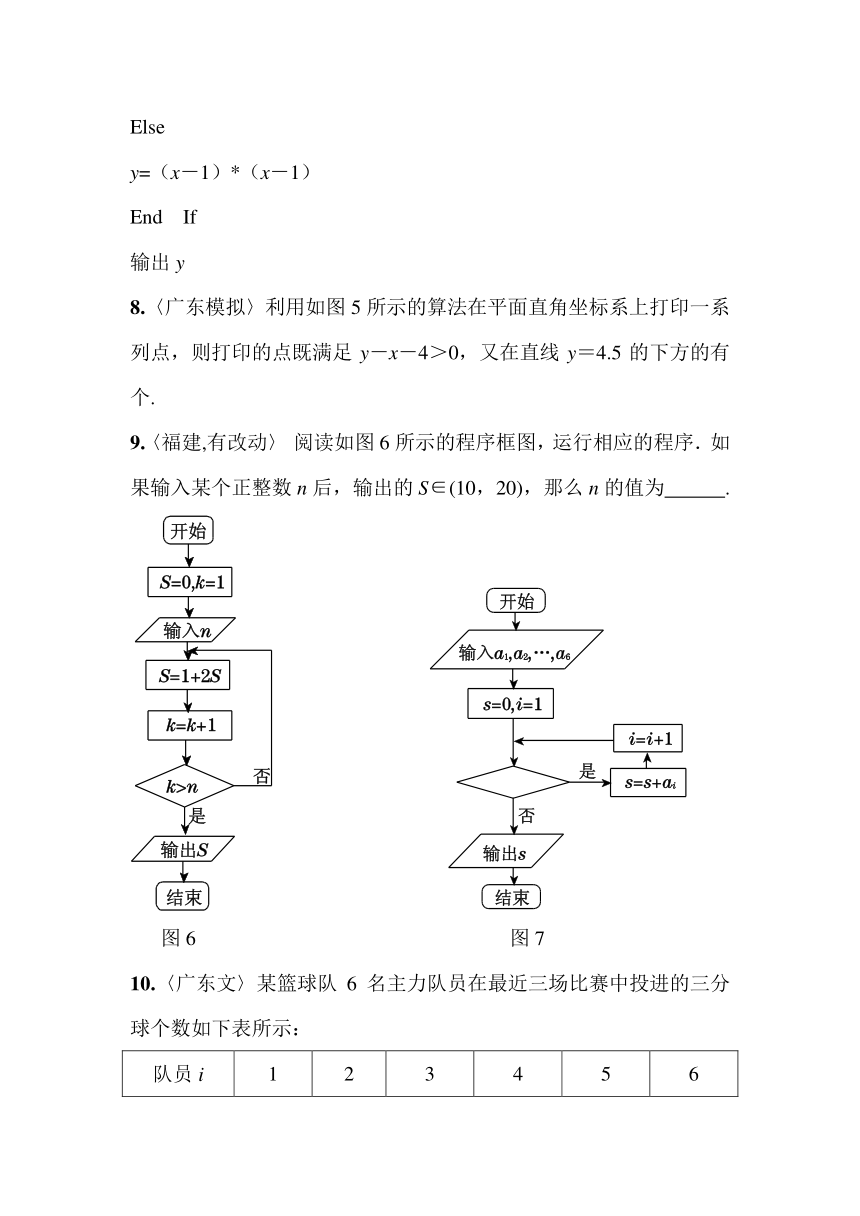
6. 已知某程序框图如图4,则该程序运行后,输出的结果为( )
A. B. C. D.
图4 图5
二、填空题(每题5分,共20分)
7.〈浙江期末考〉为了在运行下面的程序之后输出25,键盘输入的x的值应该是 .
If x<0 Then
y=(x+1)*(x+1)
Else
y=(x-1)*(x-1)
End If
输出y
8.〈广东模拟〉利用如图5所示的算法在平面直角坐标系上打印一系列点,则打印的点既满足y-x-4>0,又在直线y=4.5的下方的有 个.
9.〈福建,有改动〉 阅读如图6所示的程序框图,运行相应的程序.如果输入某个正整数n后,输出的S∈(10,20),那么n的值为 .
图6 图7
10.〈广东文〉某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
队员i
1
2
3
4
5
6
三分球个数
a1
a2
a3
a4
a5
a6
如图7所示的是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图7中判断框中应填 ,输出的s= .
三、解答题(13题18分,其余每题16分,共50分)
11. 甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图8和如图9.
图8 图9
(1)根据图8和图9,试判断甲、乙两位同学编写的程序框图输出的结果是否一致,当n=20时分别求它们输出的结果;
(2)若希望通过对图9虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的程序框图.
12.〈海南中学期末考〉数学的美是令人惊异的!如三位数153,它满足153=13+53+33,即这个整数等于它各位上的数字的立方的和,我们称这样的数为“水仙花数”.请您设计一个算法,找出大于100,小于1 000的所有“水仙花数”.
(1)用自然语言写出算法;
(2)画出流程图.
13. 某汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当每辆销售价为图10的输出结果p万元时,平均每周能售出8辆,而当每辆销售价每降低1万元时,平均每周能多售出8辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
图10
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
参考答案及点拨
一、1. C 点拨:第一步:输入n=2;第二步:n=2+1=3;第三步:n=3+1=4;第四步:输出4.故答案为C.
2. D 点拨:利用代入法求解.输入2,执行y=-1,输出-1;输入1,执行y=-1,输出-1;输入-1,执行y=(-1)3,输出-1;输入-2,执行y=(-2)3,输出-8.故选D.
3. A 学科思想:利用方程思想求解,通过输入值与输出值的关系,建立方程组求解.解方程组:得. 用户应输入:3,4,5,故选A.
4. A 点拨:由流程图可知:要判断输入的代表年份的y是否为闰年,则要判断y能否被4整除但不能被100整除,或者能否被400整除.
5. B
6. D 点拨:该程序在运行过程中各变量的值如下:A=0.2;n=1,第一次循环:A=0.4,n=2; 第二次循环:A=0.8,n=3; 第三次循环:A=0.6,n=4; 第四次循环:A=0.2,n=5;第五次循环:A=0.4,n=6,因此输出结果的周期为4.又2 013=4×503+1,因此输出结果为0.2.
二、7. 6或-6 学科思想:利用化归转化思想,将条件语句转化为分段函数问题,再利用分类讨论思想、方程思想求解.因为输出y=25,由25=(x+1)2,x<0,可得x=-6;由25=(x-1)2,x≥0,可得x=6,故x=6或-6.
8. 1 学科思想:根据算法框图的功能,写出各点坐标,然后在平面直角坐标系上,描绘出直线与各点的位置,根据数形结合思想求解.根据算法框图所示的顺序,该程序的作用是打印如下点:(-3,6),(-2,5),(-1,4),(0,3),(1,2),其中 点(-3,6),(-2,5),(-1,4)满足y-x-4>0,点(-1,4),(0,3),(1,2)在直线y=4.5的下方,即只有点(-1,4)既满足y-x-4>0,又在直线y=4.5的下方.故答案为:1.
9. 4 点拨: S=0,k=1, 第一次循环:S=1,k=2,第二次循环:S=3,k=3,第三次循环:S=7,k=4,第四次循环:S=15,k=5>4,故n的值为4.
10. i≤6;a1+a2+…+a6.
三、11. 解:(1)甲、乙两位同学编写的程序框图输出的结果是一致的.
题图8中程序框图的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.
题图9中程序框图的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.
(2)修改后虚框部分的程序框图如答图1.
答图1
12. 解:(1)算法如下:
第一步:i=101;
第二步:若i不大于999,则执行第三步,否则算法结束;
第三步:若这个数i等于它各位上的数字的立方的和,则输出这个数;
第四步:i=i+1,返回第二步.
(2)如答图2.
答图2
13. 解:(1)由程序框图知,p=29,故当每辆销售价为程序框图的输出结果p万元时,平均每周能售出8辆,则y=29-x-25=-x+4(0≤x≤4).
(2)由于当每辆销售价每降低1万元时,平均每周能多售出8辆,故每辆汽车降价x万元时,平均第周销售量为(8+8x)辆,故z=y(8+8x)=8(-x+4)(1+x)=-8x2+24x+32.
(3)∵z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4),∴当x=1.5时,平均每周的销售利润最大,此时29-x=27.5,即当每辆汽车的定价为27.5万元时.平均每周的销售利润最大,最大利润为50万元.
(100分,45分钟)
一、选择题(每题5分,共30分)
1.〈北京期末考〉如果输入2,那么执行下面算法的结果是( )
第一步:输入n
第二步:n=n+1
第三步:n=n+1
第四步:输出n
A.输出2 B.输出3
C.输出4 D.程序出错,输不出任何结果
2.〈福州模拟〉执行如图1所示的程序框图后,若输出结果为-1,则输入x的值不可能是( )
A.2 B.1 C.-1 D.-2
图1 图2
3.〈茂名二模〉某银行开发出一套网银验证程序,验证规则如下:(1)有两组数,这两组数存在一种对应关系:第一组数a,b,c对应第二组数2a+b,c+2b,a+3c;(2)进行验证时程序在电脑屏幕上依次显示出第二组数,由用户计算出第一组数后依次输入电脑,只有准确输入方能进入,其流程图如图2,试问用户应输入( )
A.3,4,5 B.4,2,6 C.2,6,4 D.3,5,7
4.〈密云一模〉如图3是关于闰年的流程图,则以下年份是闰年的为( )
图3
A.2012年 B.2010年 C.2100年 D.1998年
5. 阅读下面两个算法:
算法一: 算法二:
i=0 S=0
S=0 For i=1 To 20
Do S=S+
S=S+ Next
i=i+1 输出S
Loop While i<20
输出 S
以上两个算法( )
A.程序相同,结果相同 B.程序不同,结果相同
C.程序相同,结果不同 D.程序不同,结果不同
6. 已知某程序框图如图4,则该程序运行后,输出的结果为( )
A. B. C. D.
图4 图5
二、填空题(每题5分,共20分)
7.〈浙江期末考〉为了在运行下面的程序之后输出25,键盘输入的x的值应该是 .
If x<0 Then
y=(x+1)*(x+1)
Else
y=(x-1)*(x-1)
End If
输出y
8.〈广东模拟〉利用如图5所示的算法在平面直角坐标系上打印一系列点,则打印的点既满足y-x-4>0,又在直线y=4.5的下方的有 个.
9.〈福建,有改动〉 阅读如图6所示的程序框图,运行相应的程序.如果输入某个正整数n后,输出的S∈(10,20),那么n的值为 .
图6 图7
10.〈广东文〉某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
队员i
1
2
3
4
5
6
三分球个数
a1
a2
a3
a4
a5
a6
如图7所示的是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图7中判断框中应填 ,输出的s= .
三、解答题(13题18分,其余每题16分,共50分)
11. 甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图8和如图9.
图8 图9
(1)根据图8和图9,试判断甲、乙两位同学编写的程序框图输出的结果是否一致,当n=20时分别求它们输出的结果;
(2)若希望通过对图9虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的程序框图.
12.〈海南中学期末考〉数学的美是令人惊异的!如三位数153,它满足153=13+53+33,即这个整数等于它各位上的数字的立方的和,我们称这样的数为“水仙花数”.请您设计一个算法,找出大于100,小于1 000的所有“水仙花数”.
(1)用自然语言写出算法;
(2)画出流程图.
13. 某汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当每辆销售价为图10的输出结果p万元时,平均每周能售出8辆,而当每辆销售价每降低1万元时,平均每周能多售出8辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
图10
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
参考答案及点拨
一、1. C 点拨:第一步:输入n=2;第二步:n=2+1=3;第三步:n=3+1=4;第四步:输出4.故答案为C.
2. D 点拨:利用代入法求解.输入2,执行y=-1,输出-1;输入1,执行y=-1,输出-1;输入-1,执行y=(-1)3,输出-1;输入-2,执行y=(-2)3,输出-8.故选D.
3. A 学科思想:利用方程思想求解,通过输入值与输出值的关系,建立方程组求解.解方程组:得. 用户应输入:3,4,5,故选A.
4. A 点拨:由流程图可知:要判断输入的代表年份的y是否为闰年,则要判断y能否被4整除但不能被100整除,或者能否被400整除.
5. B
6. D 点拨:该程序在运行过程中各变量的值如下:A=0.2;n=1,第一次循环:A=0.4,n=2; 第二次循环:A=0.8,n=3; 第三次循环:A=0.6,n=4; 第四次循环:A=0.2,n=5;第五次循环:A=0.4,n=6,因此输出结果的周期为4.又2 013=4×503+1,因此输出结果为0.2.
二、7. 6或-6 学科思想:利用化归转化思想,将条件语句转化为分段函数问题,再利用分类讨论思想、方程思想求解.因为输出y=25,由25=(x+1)2,x<0,可得x=-6;由25=(x-1)2,x≥0,可得x=6,故x=6或-6.
8. 1 学科思想:根据算法框图的功能,写出各点坐标,然后在平面直角坐标系上,描绘出直线与各点的位置,根据数形结合思想求解.根据算法框图所示的顺序,该程序的作用是打印如下点:(-3,6),(-2,5),(-1,4),(0,3),(1,2),其中 点(-3,6),(-2,5),(-1,4)满足y-x-4>0,点(-1,4),(0,3),(1,2)在直线y=4.5的下方,即只有点(-1,4)既满足y-x-4>0,又在直线y=4.5的下方.故答案为:1.
9. 4 点拨: S=0,k=1, 第一次循环:S=1,k=2,第二次循环:S=3,k=3,第三次循环:S=7,k=4,第四次循环:S=15,k=5>4,故n的值为4.
10. i≤6;a1+a2+…+a6.
三、11. 解:(1)甲、乙两位同学编写的程序框图输出的结果是一致的.
题图8中程序框图的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.
题图9中程序框图的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.
(2)修改后虚框部分的程序框图如答图1.
答图1
12. 解:(1)算法如下:
第一步:i=101;
第二步:若i不大于999,则执行第三步,否则算法结束;
第三步:若这个数i等于它各位上的数字的立方的和,则输出这个数;
第四步:i=i+1,返回第二步.
(2)如答图2.
答图2
13. 解:(1)由程序框图知,p=29,故当每辆销售价为程序框图的输出结果p万元时,平均每周能售出8辆,则y=29-x-25=-x+4(0≤x≤4).
(2)由于当每辆销售价每降低1万元时,平均每周能多售出8辆,故每辆汽车降价x万元时,平均第周销售量为(8+8x)辆,故z=y(8+8x)=8(-x+4)(1+x)=-8x2+24x+32.
(3)∵z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4),∴当x=1.5时,平均每周的销售利润最大,此时29-x=27.5,即当每辆汽车的定价为27.5万元时.平均每周的销售利润最大,最大利润为50万元.
