吉林长春市七年级上册集体备课:主题与任务共建——从新课标视角看“综合与实践”课件(73张PPT)
文档属性
| 名称 | 吉林长春市七年级上册集体备课:主题与任务共建——从新课标视角看“综合与实践”课件(73张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 149.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-21 17:50:08 | ||
图片预览











文档简介
(共73张PPT)
长春市2023——2024学年度上学期七年级数学集体备课
主题与任务共建
——从新课标视角看“综合与实践”
预热:您会把一百万放在什么位置上?
会因此把一百万放在中点处吗?
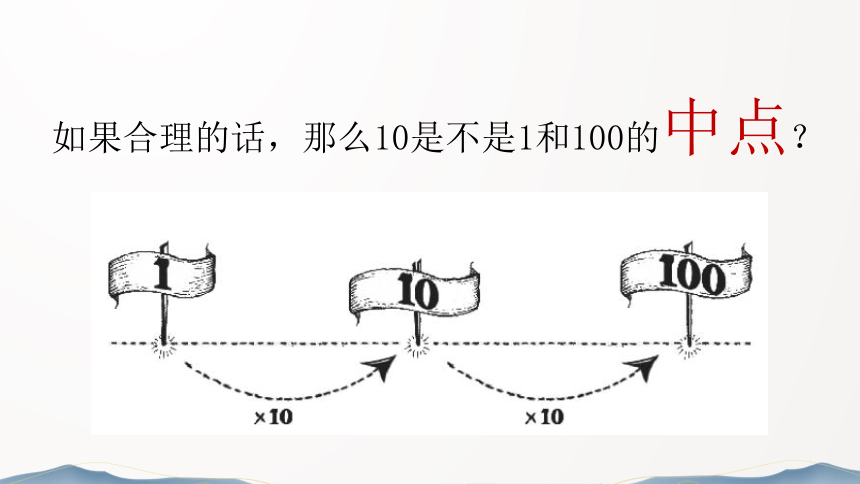
如果合理的话,那么10是不是1和100的中点?
公布:正确答案!
谁的数学DNA
动了一下
很近很近,超级近,
但并未重合哦!
综合与实践,不仅是必修的课程,
更是一种理念,一种对问题的认知方式和解决方法!
喜欢弹琴,但不必成为莫扎特。
爱上数学,但不必成为欧几里得。
在综合与实践中,找到真实的自己,成为更好的自己!
壹
设计分析
贰
课标分析
叁
教材分析
肆
案例分析
目 录
CATALOGUE
华师版七年级数学上册
01
课标分析
课标指引我们前行的方向!
华师版七年级数学上册
1. 2001版课程标准课程目标:
【双基】基础知识、基本技能
(一)对比前两版,看新标准的新视角:
2. 2011版课程标准课程目标:
【四基】基础知识、基本技能、基本思想、基本活动经验
翻
篇
开2022版数学课程标准的
新
章
3. 2022版课程标准:【四基】【四能】【三会】
(1)四基:基础知识、基本技能、基本思想、基本活动经验
(2)四能:发现和提出问题的能力、分析和解决问题的能力
(3)三会:
①会用数学的眼光观察现实世界
②会用数学的思维思考现实世界
③会用数学的语言表达现实世界
抽象能力(包括数感、量感、符号意识)、几何直观、空间观念与创新意识
数据意识或数据观念、模型意识或模型观念、应用意识
运算能力、推理意识或推理能力
添加标题
2022年版课标
2011年版课标
(1)在社会生活和科学技术的真实情境中,结合方程与不等式、函数、图形的变化、图形与坐标、抽样与数据分析等内容,经历现实情境数学化,探索数学关系、性质与规律的过程,感悟如何从数学的角度发现问题和提出问题,逐步形成“会用数学的眼光观察现实世界”的核心素养. (2)用数学的思维方法,运用数学与其他相关学科的知识,综合地、有逻辑地分析问题,经历分工合作、试验调查、建立模型、计算反思、解决问题的过程,提升思维能力,逐步形成“会用数学的思维思考现实世界”的核心素养. (3)用数学语言将现实问题转化为数学问题,经历用数学方法解决问题的过程,感悟科学研究的过程与方法,感受数学在与其他学科融合中所彰显的功效,积累数学活动经验,逐步形成“会用数学的语言表达现实世界”的核心素养.
(1)结合实际情境,经历设计解决具体问题的方案,并加以实施的过程,体验建立模型、解决问题的过程,并在此过程中,尝试发现和提出问题.
(2)会反思参与活动的全过程,将研究的过程和结果形成报告或小论文,并能进行交流,进一步获得数学活动经验.
(3)通过对有关问题的探讨,了解所学过知识(包括其他学科知识)之间的关联,进一步理解有关知识,发展应用意识和能力.
(二)比较两版课标对【综合与实践】的要求:
注重发掘合适的项目:项目式学习要关注问题是否是现实的,还要关注问题是否是跨学科的;要关注学生是否能够解决问题,还要关注学生是否能够提出问题;要关注解决问题过程中的数学计算,还要关注解决问题过程中的数学表达.这在现阶段的数学教学改革中是一项新的课题.
注重学习方式的引导:引导学生通过小组合作或独立思考,经历发现和提出问题的过程.其中,提出问题是指提出合适的数学问题.从发现问题到提出问题,往往要经历从语言表达到数学表达的过程.其中,语言表达不仅包括日常生活语言,还包括其他学科的语言.教师要帮助学生感悟如何从数学的角度审视问题,在发现和提出问题的过程中,引导学生会用数学的眼光观察现实世界.
注重引导学生经历分析和解决问题的过程.问题是由学生自己或与他人交流中提出的,解决问题的过程要与提出问题的过程有机结合,积累解决实际问题的经验.教师要帮助学生感悟解决现实问题不仅要关注数学的知识,更要关注问题的背景知识,发现问题的本质与规律,然后用数学的概念、定理或公式予以表达.在建立数学模型的过程中,引导学生会用数学的思维思考现实世界.
最终要引导学生解释数学结论的现实意义,进而解决问题.在许多情况下,模型中的参数或重要指标与所要解决问题的背景资料有关,往往需要分析模型结论的合理性,主要是分析结论是否与现实吻合.如果有悖于现实,就需要调整模型,直至合理.在这样的过程中,让学生感悟重事实、讲道理的科学精神,体会数学表达的简洁与精确,引导学生学会用数学的语言表达现实世界.
(三)新课标对【综合与实践】的教学提示:
数学
跨学科
项目式
学习
key word
我们的
关键词
key word
【综合与实践】
key word
真实
情境
自主探究
合作交流
构建、反思、解决模型
发现、提出、分析、解决问题
语言
表达
撰写
报告
02
教材分析
发掘教材中综合与实践项目的契机在哪里?
华师版七年级数学上册
教材目录
目录
华师
七上
华师版七年级上册数学教材目录
五章
30大节
10个阅读材料
2个综合与实践
01
02
03
04
整式的加减
有理数
相交线与平行线
图形的初步认识
走进数学世界
05
【五章教材目录】
数轴
三视图
线动成面
三“视”而后行
书本概念:三视图的定义、由立体图形到视图、由视图到立体图形.
一视
For example
真实情境:逮啥画啥,挑战自我.
三“视”而后行
二视
主题与任务
完成项目:用三视图的理念设计两个字、三个字、四个字的班标、名字、座右铭等.
三“视”而后行
三视
创意与生成
【10个阅读材料课程目录】
面
1.华罗庚的故事
面
观
2.幻方
3.中国人最早使用负数
4.“ ”有多大
5.从结绳记数到计算器
6.有趣的“3x+1问题”
8.用分离系数法进行整式的加减运算
7.七巧板
9.欧拉公式
10.九树成行
?
【10个阅读材料课程目录】
面
1.华罗庚的故事
面
观
2.幻方
3.中国人最早使用负数
4.“ ”有多大
5.从结绳记数到计算器
6.有趣的“3x+1问题”
8.用分离系数法进行整式的加减运算
7.七巧板
9.欧拉公式
10.九树成行
数学文化
2个综合与实践 课程目录
身份证号码与学籍号
制作包装盒
03
案例分析
最好的数学不仅是美丽的,而且是严肃的
华师版七年级数学上册
案例一
常规课程:线动成面——《“线”入为主》
案例二
阅读材料:数学历史与数轴-《历历可“数”》
案例三
综合实践:身份证号与校验-《经“验”之谈》
案例分析
案例一:《“线”入为主》点动成线,线动成面
新西兰学生的数学作业
学生钉钉画作品
北京的大兴国际机场,也是地标性建筑,是以“凤”为意象,由法国ADP Ingenierie建筑事务所和扎哈·哈迪德(Zaha Hadid)工作室设计。
上海中心大厦以龙为意向,是美国的Gensler建筑设计事务所设计的,上海中心大厦造价148亿元人民币,设计费占了7.5亿。
你知道吗?
广州塔总高度600米,世界第二、中国第一高塔。
创意最珍贵!
湖北黄石跨线景观桥撞脸“小蛮腰”
“欧协联”奖杯
广州塔是由马克·海默尔在厨房里完成了第一个塔的模型。他把一些弹性橡皮绳绑在两个椭圆形的木盘之间,一个在底部,一个在顶部。旋转顶部椭圆的时候,一个复杂的形状就出来了,这就是广州塔的最开始的构想。
广州塔
花瓶
点、线、面、体的关系
①点动成线
②线动成面
③面动成体
哪些线?
怎么动?
什么面?
一线“升级”
线的分类
图形的变换
面的分类
线段旋转
圆旋转
线段平移
线段旋转
正方形旋转
莱洛三角形
旋转
双曲线旋转
主题任务
项目目标
项目要求
完成时间
项目评价
用小木棒和彩泥拼搭、用数学尺绘制、用任何方法设计作品。
contents of a project
小组成员合作完成至少三个不同种类的作品,组内选择最佳作品进行展示交流。
作品设计完成时间:十分钟;展示交流时间:五分钟。
三个作品全部完成的前提下,每个作品加10分;展示作品由另外三个小组评分,满分分别为10分。目前总计60分。
项目评价量规
任务 计分标准 教师评价 学生互评 个人自评 合计得分
A(20—15分) B(15—10分) C(10—5分) D(5—0分) 子任务一 快速发现数学问题,准确使用数学语言表达,提出问题,主动与其他学科关联. 快速发现数学问题,准确使用数学语言表达,提出问题. 发现数学问题,准确使用数学语言表达. 发现数学问题.
子任务二 对“点动成线,线动成面”掌握非常到位,能够熟练地举出线动成面的例子,了解抛物面是由抛物线旋转产生的,能准确说明是绕着抛物线的对称轴旋转而形成的. 对“点动成线,线动成面”掌握非常到位,能够熟练地举出线动成面的例子,了解抛物面是由抛物线旋转产生的. 对“点动成线,线动成面”掌握很好,了解抛物面是由抛物线旋转产生的. 基本掌握“点动成线,线动成面”的数学原理.
子任务三 能够根据现有知识判断生活中抛物面的实例,了解凸面和凹面对平行光的反射原理,了解法线、入射角等于反射角原理;善于用数学语言表达观点. 能根据现有知识判断生活中抛物面的实例,了解凸面和凹面对平行光的反射原理,了解法线、入射角等于反射角原理. 能根据现有知识判断生活中抛物面的实例,了解凸面和凹面对平行光的反射原理. 能够根据现有知识判断生活中抛物面的实例.
子任务四 能够主动和小组成员合作商讨项目方案,设计出切实可行的实施路径,找到替代试验的操作方法,发现神秘点的位置. 能够主动和小组成员合作商讨项目方案,找到替代试验的操作方法,发现神秘点. 能够主动和小组成员合作商讨项目方案,找到替代试验的操作方法. 发现神秘点的存在.
子任务五 小组成员合作商讨与神秘点位置相关的要素,建立恰当的平面直角坐标系,找到神秘点的坐标与a的关系,给予合理的证明过程. 小组成员合作商讨与神秘点位置相关的要素,建立恰当的平面直角坐标系,找到神秘点的坐标与a的关系. 小组成员合作商讨与神秘点位置相关的要素,建立恰当的平面直角坐标系. 小组成员合作商讨与神秘点位置相关的要素.
双曲抛物面
(马鞍面)
拓展:小薯片中的大学问
直纹面
菲利克斯·坎德马鞍面建筑设计的始祖,混凝土薄壳大师作品-霍奇米洛克餐厅
“线”外之音
【再谈10个阅读材料】
面
1.华罗庚的故事
面
观
2.幻方
3.中国人最早使用负数
4.“根号2”有多大
5.从结绳记数到计算器
6.有趣的“3x+1问题”
8.用分离系数法进行整式的加减运算
7.七巧板
9.欧拉公式
10.九树成行
数学文化
任务一
利用数轴向两个方向无限延伸的性质标注数学文化发展的历史.
案例二:《历历可“数”》
数学发展史与数轴
任务二
选择一个专题,比如“镶嵌”“勾股定理”“洛书”等,用数轴标注其发展史.
任务三
借助数轴表示中国或世界历史上的重大事件.(跨学科)
公元1872年
理查德·戴德金提出无理数的概念
泰勒·笛卡尔发明了笛卡尔坐标系
公元1637年
公元1000年
杨辉三角《详解九章算法》,最早提出负数
印度阿拉伯数字产生
公元595年
公元429-500年
祖冲之将圆周率算到小数点后第七位
丢番图引入整数多项式变数,被称为算术之父
公元250年
公元100年
亚历山大数学家海伦发现虚数
《九章算术》开方和方程
公元50年
0
数学文化时间轴
印度使用9个婆罗门数字,十进制的开始
公元前50年
公元前180年
希腊几何学采用巴比伦六十进制将圆360等分
中国的《洛书》中首次出现幻方
公元前2200年
公元前300年
欧几里得发表了《几何原本》,至今仍在使用
亚里士多德《工具论》定义逻辑推理
公元前350年
公元前450年
古希腊建筑和艺术中开始使用黄金分割率
印度数学家意识到0是实际存在的数
公元前876年
公元前1100年
《周髀算经》勾股定理和分数
苏美尔人开始使用陶筹计数
公元前3400年
插播一段《幻方》
洛书九宫口诀:
戴九履一,左三右七,
二四为肩,六八为足。
4 9 2
3 5 7
8 1 6
上古伏羲氏时期
洛阳黄河
龙马
背负"河图"
大禹时期
洛阳洛河
神龟
背驮"洛书"
想你的风吹到了洛阳
杜勒作品
·
忧郁
公元前4世纪
古希腊数学家帕普斯
发现蜂巢都是六边形
15世纪艺术家
阿尔布雷希特·丢勒
发现正五边形与菱形镶嵌
公元13世纪
罗马宫殿里的马赛克
1968年
英国罗杰 彭罗斯
发现筝形和镖形拼转
1891年
苏联物理学家
弗德洛夫
——
发现十七种不同的密铺平面的对称图案
1936年
荷兰艺术家埃舍尔
将镶嵌和艺术融为一体
1619年
数学家奇帕
发现正方形镶嵌
平面镶嵌时间轴
正
大
高
多
好
负小低少差
数轴的理想
不拘一格画“数轴”
直线型数轴
曲线型数轴
环型数轴
折线型数轴
出方案
出作品
出报告
【再谈2个综合与实践 课程目录】
身份证号码与学籍号
制作包装盒
案例三:《经“验”之谈》
身份证号码与校验码
问题清单
问题1:
身份证号码代表的意义?
问题2:
最后一位为什么有“X”?
问题3:
校验法是谁开创的?
问题4:
什么是弃九法?
问题5:
生活中哪些需要校验?
问题6:
设计一个可校验的学号
见自我
X是校验码
它不是英文字母
而是罗马数字10
身份证号码是根据〖中华人民共和国国家标准GB11643-1999〗中有关公民身份号码的规定,根据精密的计算公式计算出来的,公民身份号码是特征组合码,由十七位数字本体码和一位数字校验码组成。排列顺序从左至右依次为:六位数字地址码(省-市-区),八位数字出生日期码(年-月-日),三位数字顺序码(派出所-性别),最后一位是数字校验码。
校 验
算 法
起 源
撒马尔罕城
皇帝:兀鲁伯格
科学家:阿尔·卡西
《算术之钥》
弃九法
见自我
弃九法
弃九数:
例如:数字1978,1+9+7+8=25(大于9)
继续运算:2+5=7
此时7就是原数1978的弃九数
实际上,7也是1978÷9的余数.
证明: ABCD
=1000A+100B+10C+D=(999+1)A+(99+1)B+(9+1)C+D
=999A+99B+9C+(A+B+C+D)=9(111A+11B+C)+(A+B+C+D)
验证:3169×732=2319708
3169的弃九数为1,732的弃九数为3,2319708的弃九数为3
因为1×3=3
因此,结果很可能是正确的
将前面的身份证号码17位数分别乘以不同的系数。
规定从第一位到第十七位的系数分别为:
7 9 10 5 8 4 2 1 6 3 7 9 10 5 8 4 2
将这17位数字和系数相乘的结果相加
用加出来和除以11,看余数是多少?
余数只可能有0 1 2 3 4 5 6 7 8 9 10这11个数字。
其分别对应的最后一位身份证的号码为1 0 X 9 8 7 6 5 4 3 2;
通过上面得知如果余数是2,就会在身份证的第18位数字上出现罗马数字的Ⅹ。如果余数是10,身份证的最后一位号码就是2.
身份证号码中的校验码(弃11法)
加权因子
还有谁?需要校验?
主题任务:
为全校学生设计一个可校验的学号
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
04
开发思路分析
你看到的世界,往往是你想看到的世界
华师版七年级数学上册
熵增定律
克劳修斯提出的热力学定律
时时勤拂拭,勿使惹尘埃
结构信息
结构信息量越大,系统越有序。
信息意味着负熵、反熵增或熵减。
物理→跨学科
学习如人生,只有在
抗“熵”的路上越走越远,我们才有可能不断走向成功!
实
战
演
练
——以《打开天窗说“量”话》为例谈综合实践课的设计开发思路
设计灵感
思
考
测量历史
测量工具
测量分类
测量任务
测量方法
学生讲述自己所了解的关于计量的发展史
思考计量学对科技发展及生活的意义
天马行空的谈谈自己的测量理想
交流分享关于测量的小窍门
科技要发展,计量需先行
测量目标分类汇总
一维
二维
三维
小线人儿
纸片人儿
立体人儿
他好高啊!
测量对象
测量目标分类汇总
一维
二维
三维
小线人儿
纸片人儿
立体人儿
他好高啊!
一维长度容易量?
化曲为直
探究操作(一):测量不规则管道的长度
活动要求:
1.桌面上有一条形状不规则的实物曲线,思考如何测量曲线的长度,才能尽可能减小测量误差;
2.讨论不同方法的利弊,并选出小组最优方案由小组代表进行汇报展示;
3.活动时间:2分钟.
一维长度容易量?
由内及外
A
B
D
C
C1
探究操作(二):测量封闭长方体最长对角线的长度
活动要求:
1.长方体盒子是封闭的、不能拆开、不能将尺直接伸入盒内,选择恰当的方法测量如图所示的最长对角线的长度;
2.选择最优方案并由小组代表进行汇报展示;
3.活动时间:2分钟。
万事俱备,
只缺太阳!
探究操作(三):测量升旗杆的高度
以小见大
太阳和我一样公平
二维面积难测量?
探究操作(四):测量不规则污渍的面积
三角形
圆
不规则污渍
二维面积难测量?
10
20
30
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
探究操作(四):测量不规则污渍的面积
活动要求:
1.桌面上有一张有污渍的方格纸,每个小方格的面积都是单位1;
2.请尽可能让测量结果接近准确面积的数值,并和大家分享一下你的想法;
3.活动时间:2分钟.
圆柱体
三维体积怎么量?
长方体
圆柱体
球体
心有多大,
世界就有多大!
三维体积怎么量?
探究操作(五):测量心脏的体积
活动要求:
1.桌面上有水槽,有烧杯,有量筒,有足够的水,借助这些工具测量你的“心”的大小;
2.选出你们小组“心”最大的人,发表二十秒获奖感言;
3.活动时间:3分钟.
地球:你问我爱你有多深?
半径代表我的心!
知识延伸(六):测量地球的半径
迪拜哈利法塔
优化方案
有 形
无 形
四 维
智慧难以言传,唯有经历才可获得。
数学的智慧正是如此,综合与实践的意义也正是如此。
综合与实践
四重境界
见知识
01
见自我
02
见天地
03
04
04
见众生
THANK YOU
深深感谢,恳请批评指正!
education and teaching
华师版七年级数学上册
长春市2023——2024学年度上学期七年级数学集体备课
主题与任务共建
——从新课标视角看“综合与实践”
预热:您会把一百万放在什么位置上?
会因此把一百万放在中点处吗?
如果合理的话,那么10是不是1和100的中点?
公布:正确答案!
谁的数学DNA
动了一下
很近很近,超级近,
但并未重合哦!
综合与实践,不仅是必修的课程,
更是一种理念,一种对问题的认知方式和解决方法!
喜欢弹琴,但不必成为莫扎特。
爱上数学,但不必成为欧几里得。
在综合与实践中,找到真实的自己,成为更好的自己!
壹
设计分析
贰
课标分析
叁
教材分析
肆
案例分析
目 录
CATALOGUE
华师版七年级数学上册
01
课标分析
课标指引我们前行的方向!
华师版七年级数学上册
1. 2001版课程标准课程目标:
【双基】基础知识、基本技能
(一)对比前两版,看新标准的新视角:
2. 2011版课程标准课程目标:
【四基】基础知识、基本技能、基本思想、基本活动经验
翻
篇
开2022版数学课程标准的
新
章
3. 2022版课程标准:【四基】【四能】【三会】
(1)四基:基础知识、基本技能、基本思想、基本活动经验
(2)四能:发现和提出问题的能力、分析和解决问题的能力
(3)三会:
①会用数学的眼光观察现实世界
②会用数学的思维思考现实世界
③会用数学的语言表达现实世界
抽象能力(包括数感、量感、符号意识)、几何直观、空间观念与创新意识
数据意识或数据观念、模型意识或模型观念、应用意识
运算能力、推理意识或推理能力
添加标题
2022年版课标
2011年版课标
(1)在社会生活和科学技术的真实情境中,结合方程与不等式、函数、图形的变化、图形与坐标、抽样与数据分析等内容,经历现实情境数学化,探索数学关系、性质与规律的过程,感悟如何从数学的角度发现问题和提出问题,逐步形成“会用数学的眼光观察现实世界”的核心素养. (2)用数学的思维方法,运用数学与其他相关学科的知识,综合地、有逻辑地分析问题,经历分工合作、试验调查、建立模型、计算反思、解决问题的过程,提升思维能力,逐步形成“会用数学的思维思考现实世界”的核心素养. (3)用数学语言将现实问题转化为数学问题,经历用数学方法解决问题的过程,感悟科学研究的过程与方法,感受数学在与其他学科融合中所彰显的功效,积累数学活动经验,逐步形成“会用数学的语言表达现实世界”的核心素养.
(1)结合实际情境,经历设计解决具体问题的方案,并加以实施的过程,体验建立模型、解决问题的过程,并在此过程中,尝试发现和提出问题.
(2)会反思参与活动的全过程,将研究的过程和结果形成报告或小论文,并能进行交流,进一步获得数学活动经验.
(3)通过对有关问题的探讨,了解所学过知识(包括其他学科知识)之间的关联,进一步理解有关知识,发展应用意识和能力.
(二)比较两版课标对【综合与实践】的要求:
注重发掘合适的项目:项目式学习要关注问题是否是现实的,还要关注问题是否是跨学科的;要关注学生是否能够解决问题,还要关注学生是否能够提出问题;要关注解决问题过程中的数学计算,还要关注解决问题过程中的数学表达.这在现阶段的数学教学改革中是一项新的课题.
注重学习方式的引导:引导学生通过小组合作或独立思考,经历发现和提出问题的过程.其中,提出问题是指提出合适的数学问题.从发现问题到提出问题,往往要经历从语言表达到数学表达的过程.其中,语言表达不仅包括日常生活语言,还包括其他学科的语言.教师要帮助学生感悟如何从数学的角度审视问题,在发现和提出问题的过程中,引导学生会用数学的眼光观察现实世界.
注重引导学生经历分析和解决问题的过程.问题是由学生自己或与他人交流中提出的,解决问题的过程要与提出问题的过程有机结合,积累解决实际问题的经验.教师要帮助学生感悟解决现实问题不仅要关注数学的知识,更要关注问题的背景知识,发现问题的本质与规律,然后用数学的概念、定理或公式予以表达.在建立数学模型的过程中,引导学生会用数学的思维思考现实世界.
最终要引导学生解释数学结论的现实意义,进而解决问题.在许多情况下,模型中的参数或重要指标与所要解决问题的背景资料有关,往往需要分析模型结论的合理性,主要是分析结论是否与现实吻合.如果有悖于现实,就需要调整模型,直至合理.在这样的过程中,让学生感悟重事实、讲道理的科学精神,体会数学表达的简洁与精确,引导学生学会用数学的语言表达现实世界.
(三)新课标对【综合与实践】的教学提示:
数学
跨学科
项目式
学习
key word
我们的
关键词
key word
【综合与实践】
key word
真实
情境
自主探究
合作交流
构建、反思、解决模型
发现、提出、分析、解决问题
语言
表达
撰写
报告
02
教材分析
发掘教材中综合与实践项目的契机在哪里?
华师版七年级数学上册
教材目录
目录
华师
七上
华师版七年级上册数学教材目录
五章
30大节
10个阅读材料
2个综合与实践
01
02
03
04
整式的加减
有理数
相交线与平行线
图形的初步认识
走进数学世界
05
【五章教材目录】
数轴
三视图
线动成面
三“视”而后行
书本概念:三视图的定义、由立体图形到视图、由视图到立体图形.
一视
For example
真实情境:逮啥画啥,挑战自我.
三“视”而后行
二视
主题与任务
完成项目:用三视图的理念设计两个字、三个字、四个字的班标、名字、座右铭等.
三“视”而后行
三视
创意与生成
【10个阅读材料课程目录】
面
1.华罗庚的故事
面
观
2.幻方
3.中国人最早使用负数
4.“ ”有多大
5.从结绳记数到计算器
6.有趣的“3x+1问题”
8.用分离系数法进行整式的加减运算
7.七巧板
9.欧拉公式
10.九树成行
?
【10个阅读材料课程目录】
面
1.华罗庚的故事
面
观
2.幻方
3.中国人最早使用负数
4.“ ”有多大
5.从结绳记数到计算器
6.有趣的“3x+1问题”
8.用分离系数法进行整式的加减运算
7.七巧板
9.欧拉公式
10.九树成行
数学文化
2个综合与实践 课程目录
身份证号码与学籍号
制作包装盒
03
案例分析
最好的数学不仅是美丽的,而且是严肃的
华师版七年级数学上册
案例一
常规课程:线动成面——《“线”入为主》
案例二
阅读材料:数学历史与数轴-《历历可“数”》
案例三
综合实践:身份证号与校验-《经“验”之谈》
案例分析
案例一:《“线”入为主》点动成线,线动成面
新西兰学生的数学作业
学生钉钉画作品
北京的大兴国际机场,也是地标性建筑,是以“凤”为意象,由法国ADP Ingenierie建筑事务所和扎哈·哈迪德(Zaha Hadid)工作室设计。
上海中心大厦以龙为意向,是美国的Gensler建筑设计事务所设计的,上海中心大厦造价148亿元人民币,设计费占了7.5亿。
你知道吗?
广州塔总高度600米,世界第二、中国第一高塔。
创意最珍贵!
湖北黄石跨线景观桥撞脸“小蛮腰”
“欧协联”奖杯
广州塔是由马克·海默尔在厨房里完成了第一个塔的模型。他把一些弹性橡皮绳绑在两个椭圆形的木盘之间,一个在底部,一个在顶部。旋转顶部椭圆的时候,一个复杂的形状就出来了,这就是广州塔的最开始的构想。
广州塔
花瓶
点、线、面、体的关系
①点动成线
②线动成面
③面动成体
哪些线?
怎么动?
什么面?
一线“升级”
线的分类
图形的变换
面的分类
线段旋转
圆旋转
线段平移
线段旋转
正方形旋转
莱洛三角形
旋转
双曲线旋转
主题任务
项目目标
项目要求
完成时间
项目评价
用小木棒和彩泥拼搭、用数学尺绘制、用任何方法设计作品。
contents of a project
小组成员合作完成至少三个不同种类的作品,组内选择最佳作品进行展示交流。
作品设计完成时间:十分钟;展示交流时间:五分钟。
三个作品全部完成的前提下,每个作品加10分;展示作品由另外三个小组评分,满分分别为10分。目前总计60分。
项目评价量规
任务 计分标准 教师评价 学生互评 个人自评 合计得分
A(20—15分) B(15—10分) C(10—5分) D(5—0分) 子任务一 快速发现数学问题,准确使用数学语言表达,提出问题,主动与其他学科关联. 快速发现数学问题,准确使用数学语言表达,提出问题. 发现数学问题,准确使用数学语言表达. 发现数学问题.
子任务二 对“点动成线,线动成面”掌握非常到位,能够熟练地举出线动成面的例子,了解抛物面是由抛物线旋转产生的,能准确说明是绕着抛物线的对称轴旋转而形成的. 对“点动成线,线动成面”掌握非常到位,能够熟练地举出线动成面的例子,了解抛物面是由抛物线旋转产生的. 对“点动成线,线动成面”掌握很好,了解抛物面是由抛物线旋转产生的. 基本掌握“点动成线,线动成面”的数学原理.
子任务三 能够根据现有知识判断生活中抛物面的实例,了解凸面和凹面对平行光的反射原理,了解法线、入射角等于反射角原理;善于用数学语言表达观点. 能根据现有知识判断生活中抛物面的实例,了解凸面和凹面对平行光的反射原理,了解法线、入射角等于反射角原理. 能根据现有知识判断生活中抛物面的实例,了解凸面和凹面对平行光的反射原理. 能够根据现有知识判断生活中抛物面的实例.
子任务四 能够主动和小组成员合作商讨项目方案,设计出切实可行的实施路径,找到替代试验的操作方法,发现神秘点的位置. 能够主动和小组成员合作商讨项目方案,找到替代试验的操作方法,发现神秘点. 能够主动和小组成员合作商讨项目方案,找到替代试验的操作方法. 发现神秘点的存在.
子任务五 小组成员合作商讨与神秘点位置相关的要素,建立恰当的平面直角坐标系,找到神秘点的坐标与a的关系,给予合理的证明过程. 小组成员合作商讨与神秘点位置相关的要素,建立恰当的平面直角坐标系,找到神秘点的坐标与a的关系. 小组成员合作商讨与神秘点位置相关的要素,建立恰当的平面直角坐标系. 小组成员合作商讨与神秘点位置相关的要素.
双曲抛物面
(马鞍面)
拓展:小薯片中的大学问
直纹面
菲利克斯·坎德马鞍面建筑设计的始祖,混凝土薄壳大师作品-霍奇米洛克餐厅
“线”外之音
【再谈10个阅读材料】
面
1.华罗庚的故事
面
观
2.幻方
3.中国人最早使用负数
4.“根号2”有多大
5.从结绳记数到计算器
6.有趣的“3x+1问题”
8.用分离系数法进行整式的加减运算
7.七巧板
9.欧拉公式
10.九树成行
数学文化
任务一
利用数轴向两个方向无限延伸的性质标注数学文化发展的历史.
案例二:《历历可“数”》
数学发展史与数轴
任务二
选择一个专题,比如“镶嵌”“勾股定理”“洛书”等,用数轴标注其发展史.
任务三
借助数轴表示中国或世界历史上的重大事件.(跨学科)
公元1872年
理查德·戴德金提出无理数的概念
泰勒·笛卡尔发明了笛卡尔坐标系
公元1637年
公元1000年
杨辉三角《详解九章算法》,最早提出负数
印度阿拉伯数字产生
公元595年
公元429-500年
祖冲之将圆周率算到小数点后第七位
丢番图引入整数多项式变数,被称为算术之父
公元250年
公元100年
亚历山大数学家海伦发现虚数
《九章算术》开方和方程
公元50年
0
数学文化时间轴
印度使用9个婆罗门数字,十进制的开始
公元前50年
公元前180年
希腊几何学采用巴比伦六十进制将圆360等分
中国的《洛书》中首次出现幻方
公元前2200年
公元前300年
欧几里得发表了《几何原本》,至今仍在使用
亚里士多德《工具论》定义逻辑推理
公元前350年
公元前450年
古希腊建筑和艺术中开始使用黄金分割率
印度数学家意识到0是实际存在的数
公元前876年
公元前1100年
《周髀算经》勾股定理和分数
苏美尔人开始使用陶筹计数
公元前3400年
插播一段《幻方》
洛书九宫口诀:
戴九履一,左三右七,
二四为肩,六八为足。
4 9 2
3 5 7
8 1 6
上古伏羲氏时期
洛阳黄河
龙马
背负"河图"
大禹时期
洛阳洛河
神龟
背驮"洛书"
想你的风吹到了洛阳
杜勒作品
·
忧郁
公元前4世纪
古希腊数学家帕普斯
发现蜂巢都是六边形
15世纪艺术家
阿尔布雷希特·丢勒
发现正五边形与菱形镶嵌
公元13世纪
罗马宫殿里的马赛克
1968年
英国罗杰 彭罗斯
发现筝形和镖形拼转
1891年
苏联物理学家
弗德洛夫
——
发现十七种不同的密铺平面的对称图案
1936年
荷兰艺术家埃舍尔
将镶嵌和艺术融为一体
1619年
数学家奇帕
发现正方形镶嵌
平面镶嵌时间轴
正
大
高
多
好
负小低少差
数轴的理想
不拘一格画“数轴”
直线型数轴
曲线型数轴
环型数轴
折线型数轴
出方案
出作品
出报告
【再谈2个综合与实践 课程目录】
身份证号码与学籍号
制作包装盒
案例三:《经“验”之谈》
身份证号码与校验码
问题清单
问题1:
身份证号码代表的意义?
问题2:
最后一位为什么有“X”?
问题3:
校验法是谁开创的?
问题4:
什么是弃九法?
问题5:
生活中哪些需要校验?
问题6:
设计一个可校验的学号
见自我
X是校验码
它不是英文字母
而是罗马数字10
身份证号码是根据〖中华人民共和国国家标准GB11643-1999〗中有关公民身份号码的规定,根据精密的计算公式计算出来的,公民身份号码是特征组合码,由十七位数字本体码和一位数字校验码组成。排列顺序从左至右依次为:六位数字地址码(省-市-区),八位数字出生日期码(年-月-日),三位数字顺序码(派出所-性别),最后一位是数字校验码。
校 验
算 法
起 源
撒马尔罕城
皇帝:兀鲁伯格
科学家:阿尔·卡西
《算术之钥》
弃九法
见自我
弃九法
弃九数:
例如:数字1978,1+9+7+8=25(大于9)
继续运算:2+5=7
此时7就是原数1978的弃九数
实际上,7也是1978÷9的余数.
证明: ABCD
=1000A+100B+10C+D=(999+1)A+(99+1)B+(9+1)C+D
=999A+99B+9C+(A+B+C+D)=9(111A+11B+C)+(A+B+C+D)
验证:3169×732=2319708
3169的弃九数为1,732的弃九数为3,2319708的弃九数为3
因为1×3=3
因此,结果很可能是正确的
将前面的身份证号码17位数分别乘以不同的系数。
规定从第一位到第十七位的系数分别为:
7 9 10 5 8 4 2 1 6 3 7 9 10 5 8 4 2
将这17位数字和系数相乘的结果相加
用加出来和除以11,看余数是多少?
余数只可能有0 1 2 3 4 5 6 7 8 9 10这11个数字。
其分别对应的最后一位身份证的号码为1 0 X 9 8 7 6 5 4 3 2;
通过上面得知如果余数是2,就会在身份证的第18位数字上出现罗马数字的Ⅹ。如果余数是10,身份证的最后一位号码就是2.
身份证号码中的校验码(弃11法)
加权因子
还有谁?需要校验?
主题任务:
为全校学生设计一个可校验的学号
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
姓名:
班级:
学号:
04
开发思路分析
你看到的世界,往往是你想看到的世界
华师版七年级数学上册
熵增定律
克劳修斯提出的热力学定律
时时勤拂拭,勿使惹尘埃
结构信息
结构信息量越大,系统越有序。
信息意味着负熵、反熵增或熵减。
物理→跨学科
学习如人生,只有在
抗“熵”的路上越走越远,我们才有可能不断走向成功!
实
战
演
练
——以《打开天窗说“量”话》为例谈综合实践课的设计开发思路
设计灵感
思
考
测量历史
测量工具
测量分类
测量任务
测量方法
学生讲述自己所了解的关于计量的发展史
思考计量学对科技发展及生活的意义
天马行空的谈谈自己的测量理想
交流分享关于测量的小窍门
科技要发展,计量需先行
测量目标分类汇总
一维
二维
三维
小线人儿
纸片人儿
立体人儿
他好高啊!
测量对象
测量目标分类汇总
一维
二维
三维
小线人儿
纸片人儿
立体人儿
他好高啊!
一维长度容易量?
化曲为直
探究操作(一):测量不规则管道的长度
活动要求:
1.桌面上有一条形状不规则的实物曲线,思考如何测量曲线的长度,才能尽可能减小测量误差;
2.讨论不同方法的利弊,并选出小组最优方案由小组代表进行汇报展示;
3.活动时间:2分钟.
一维长度容易量?
由内及外
A
B
D
C
C1
探究操作(二):测量封闭长方体最长对角线的长度
活动要求:
1.长方体盒子是封闭的、不能拆开、不能将尺直接伸入盒内,选择恰当的方法测量如图所示的最长对角线的长度;
2.选择最优方案并由小组代表进行汇报展示;
3.活动时间:2分钟。
万事俱备,
只缺太阳!
探究操作(三):测量升旗杆的高度
以小见大
太阳和我一样公平
二维面积难测量?
探究操作(四):测量不规则污渍的面积
三角形
圆
不规则污渍
二维面积难测量?
10
20
30
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
探究操作(四):测量不规则污渍的面积
活动要求:
1.桌面上有一张有污渍的方格纸,每个小方格的面积都是单位1;
2.请尽可能让测量结果接近准确面积的数值,并和大家分享一下你的想法;
3.活动时间:2分钟.
圆柱体
三维体积怎么量?
长方体
圆柱体
球体
心有多大,
世界就有多大!
三维体积怎么量?
探究操作(五):测量心脏的体积
活动要求:
1.桌面上有水槽,有烧杯,有量筒,有足够的水,借助这些工具测量你的“心”的大小;
2.选出你们小组“心”最大的人,发表二十秒获奖感言;
3.活动时间:3分钟.
地球:你问我爱你有多深?
半径代表我的心!
知识延伸(六):测量地球的半径
迪拜哈利法塔
优化方案
有 形
无 形
四 维
智慧难以言传,唯有经历才可获得。
数学的智慧正是如此,综合与实践的意义也正是如此。
综合与实践
四重境界
见知识
01
见自我
02
见天地
03
04
04
见众生
THANK YOU
深深感谢,恳请批评指正!
education and teaching
华师版七年级数学上册
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
