2.11二次函数与一元二次方程1(广东省深圳市)
文档属性
| 名称 | 2.11二次函数与一元二次方程1(广东省深圳市) |

|
|
| 格式 | rar | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-17 00:00:00 | ||
图片预览


文档简介
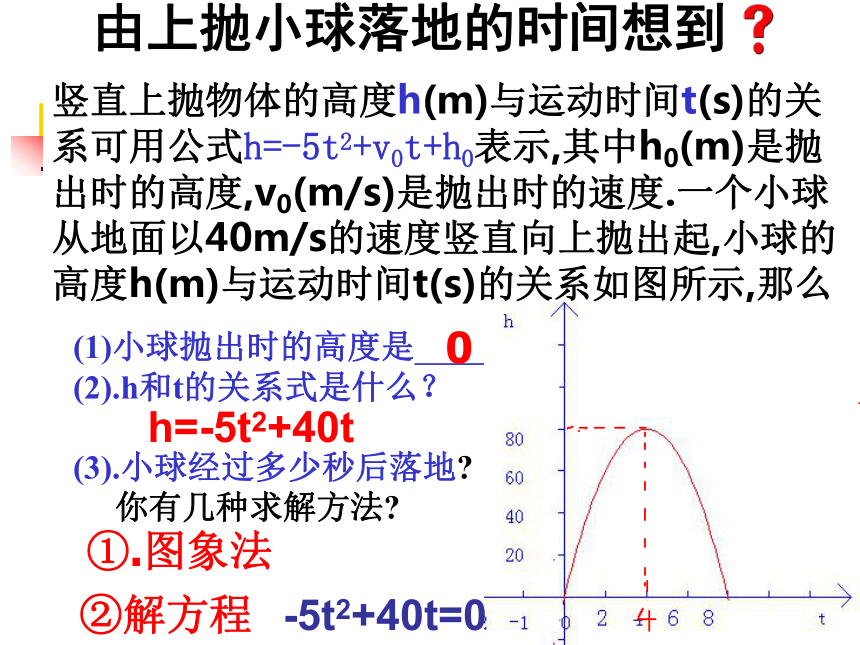
课件10张PPT。初三数学备课组二次函数与一元二次方程1(1)小球抛出时的高度是 ,
(2).h和t的关系式是什么?
(3).小球经过多少秒后落地?
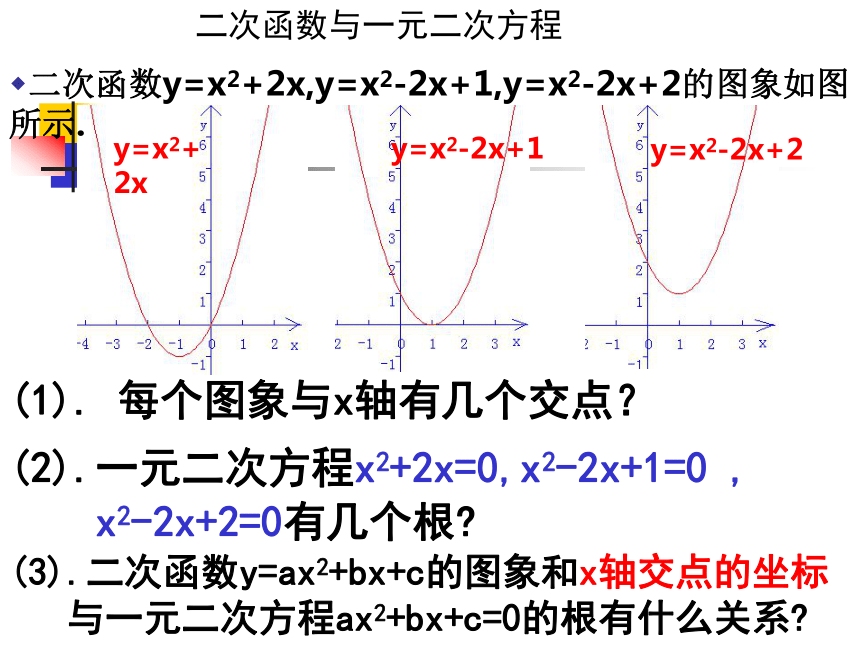
你有几种求解方法?由上抛小球落地的时间想到 竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么h=-5t2+40t①.图象法②解方程-5t2+40t=00(1). 每个图象与x轴有几个交点?二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2(2).一元二次方程x2+2x=0,x2-2x+1=0 ,
x2-2x+2=0有几个根? (3).二次函数y=ax2+bx+c的图象和x轴交点的坐标
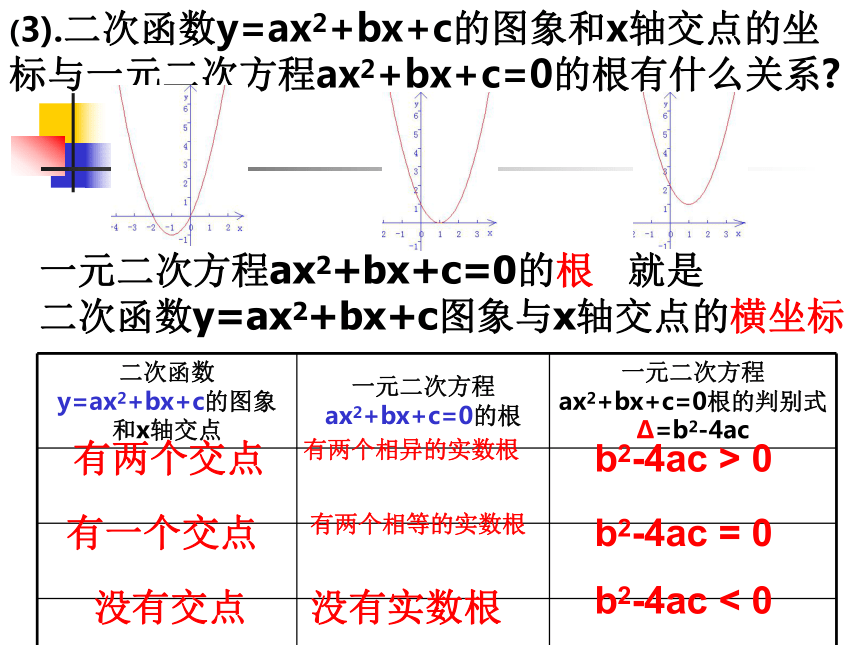
与一元二次方程ax2+bx+c=0的根有什么关系?(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0一元二次方程ax2+bx+c=0的根 就是
二次函数y=ax2+bx+c图象与x轴交点的横坐标二、基础训练 1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;3、已知抛物线y=x2+px+q与x轴的两个交点(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多
只有一个交点,则a的范围是 。9a<9-1-65、判断下列各抛物线是否与x轴相交,
如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8 4、校运会上,某运动员掷铅球,铅
球的高y(m)与水平距离x(m)之间函数关系式为y=-0.2x2+1.6x+1.8,则此运动员的成绩是 m,96、根据各个图象的信息估计一元二次方程的解 2、已知抛物线y=ax2+bx+c的顶点为
(1,-4)与x轴两交点坐标分别为
(x1,0),(x2,0),且x12+x22=10,求抛物线的解析式。三、例题 1、抛物线y=ax2+bx+c(a≠0)的图象全
部在x轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0D2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,
求m的值。四、课堂训练《1+1》P54-55
(2).h和t的关系式是什么?
(3).小球经过多少秒后落地?
你有几种求解方法?由上抛小球落地的时间想到 竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么h=-5t2+40t①.图象法②解方程-5t2+40t=00(1). 每个图象与x轴有几个交点?二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2(2).一元二次方程x2+2x=0,x2-2x+1=0 ,
x2-2x+2=0有几个根? (3).二次函数y=ax2+bx+c的图象和x轴交点的坐标
与一元二次方程ax2+bx+c=0的根有什么关系?(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0一元二次方程ax2+bx+c=0的根 就是
二次函数y=ax2+bx+c图象与x轴交点的横坐标二、基础训练 1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;3、已知抛物线y=x2+px+q与x轴的两个交点(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多
只有一个交点,则a的范围是 。9a<9-1-65、判断下列各抛物线是否与x轴相交,
如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8 4、校运会上,某运动员掷铅球,铅
球的高y(m)与水平距离x(m)之间函数关系式为y=-0.2x2+1.6x+1.8,则此运动员的成绩是 m,96、根据各个图象的信息估计一元二次方程的解 2、已知抛物线y=ax2+bx+c的顶点为
(1,-4)与x轴两交点坐标分别为
(x1,0),(x2,0),且x12+x22=10,求抛物线的解析式。三、例题 1、抛物线y=ax2+bx+c(a≠0)的图象全
部在x轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0D2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,
求m的值。四、课堂训练《1+1》P54-55
