整式2(湖北省十堰市竹溪县)
文档属性
| 名称 | 整式2(湖北省十堰市竹溪县) |  | |
| 格式 | rar | ||
| 文件大小 | 385.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-21 20:13:00 | ||
图片预览




文档简介
课件12张PPT。1、什么叫单项式?举例说明.2、怎样确定一个单项式的系数和次数?
的系数和次数分别是多少?4、设n表示任意一个整数,利用含n的式子表示:
(1)任意一个偶数(2)任意一个奇数第二课时 多项式整式的加减填空,然后分析所填式子的特点:1.一个数比数X的2倍小3,则这个数为________°C
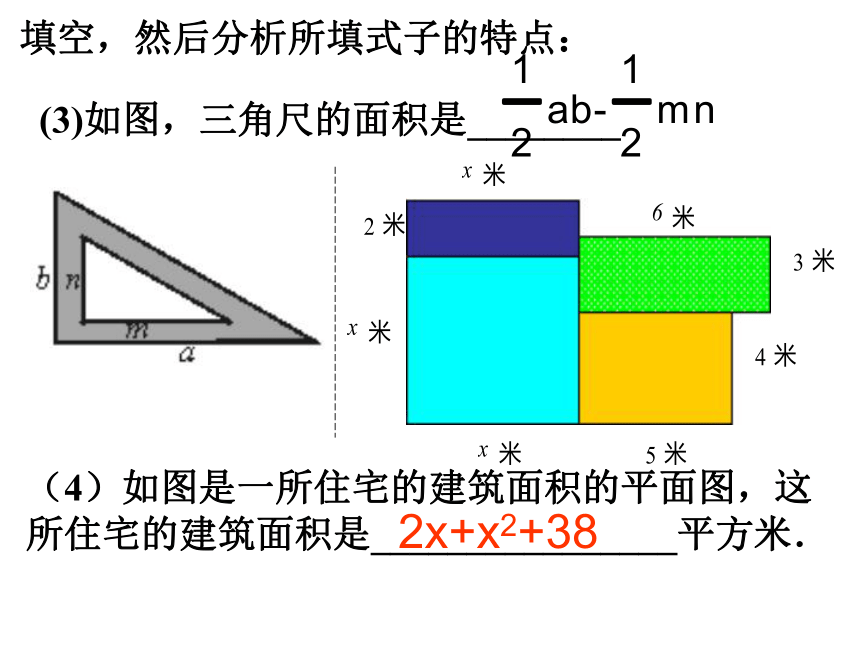
2.买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要__________ 元 2x-33x+5y+2z填空,然后分析所填式子的特点:(3)如图,三角尺的面积是________ (4)如图是一所住宅的建筑面积的平面图,这所住宅的建筑面积是________________平方米. 2x+x2+38归纳:1、多项式:几个单项式的和叫作多项式;3、次数:多项式里次数最高的项的次
数叫作这个多项式的次数.2、项:在多项式中每一个单项式叫作
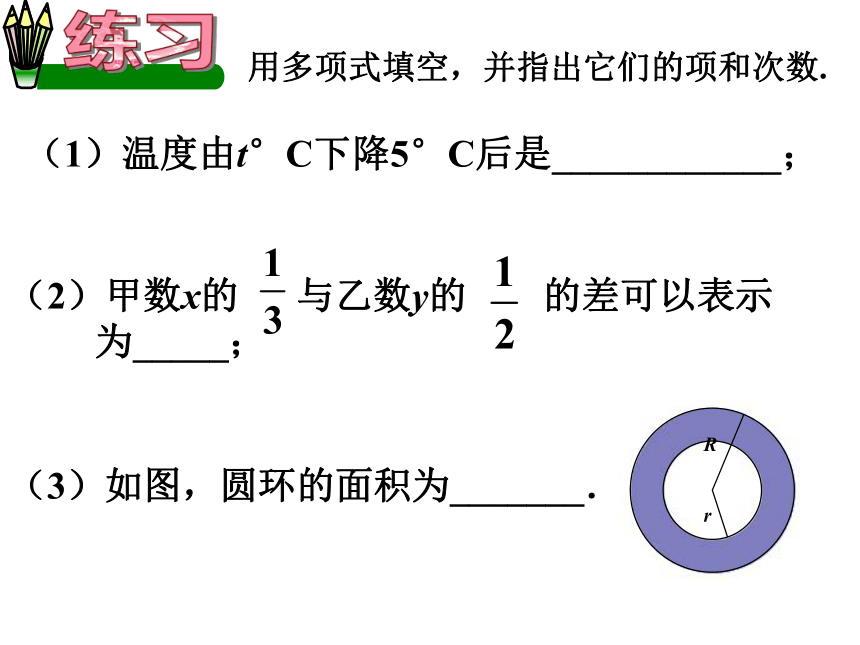
多项式的项,其中不字母的项叫作常数项;用多项式填空,并指出它们的项和次数. (1)温度由t°C下降5°C后是____________; (2)甲数x的 与乙数y的 的差可以表示
为_____; (3)如图,圆环的面积为_______. 一 下列式子中,哪些是单项式?哪些是多项式?哪些是整式?单项式:多项式:整式:(1)多项式 的次数是2 ( )(2)多项式 的一次项系数是1 ( )(3) 是三次三项式 ( )二 判断题:2、多项式的项应包括它前面的符号;多项式没有系数,但每一项都有系数,每一项系也应包括它前面的符号.3、多项式次数与单项式次数不同,但又有联系,首先应求出多项式中各项(单项式)的次数,次数最高的就是这个多项式的次数.4、一个多项式最高次次项不唯一,次高次项也不唯一.1、整式的概念;单项式、多项式以及相关概念. 例:一条河流的水流速为2.5千米/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?如果甲、乙两条船在静水中的速度分别是20千米/时和35千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度分别是多少? 解:设船在静水中的速度是v千米/小时,则
当船顺水行驶时,船的速度为(v+2.5)千米/时.
当船逆水行驶时,船的速度为(v-2.5)千米/时.
若甲船在静水中的速度是20千米/时,即v=20,则
v+2.5=20+2.5=22.5;
v-2.5=20-2.5=17.5.
若乙船在静水中的速度是35千米/时,即v=35,则
v+2.5=35+2.5=37.5;
v-2.5=35-2.5=32.5.
由上可知,甲船顺水行驶的速度是22.5千米/时,逆
水行驶的速度是17.5千米/时;
乙船顺水行驶的速度是37.5千米/时,逆水行驶的速
度是32.5千米/时. 记事:本课按些课件讲时,注意在第八张后讲要向学生介绍整式的概念,及多项式的说法
的系数和次数分别是多少?4、设n表示任意一个整数,利用含n的式子表示:
(1)任意一个偶数(2)任意一个奇数第二课时 多项式整式的加减填空,然后分析所填式子的特点:1.一个数比数X的2倍小3,则这个数为________°C
2.买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要__________ 元 2x-33x+5y+2z填空,然后分析所填式子的特点:(3)如图,三角尺的面积是________ (4)如图是一所住宅的建筑面积的平面图,这所住宅的建筑面积是________________平方米. 2x+x2+38归纳:1、多项式:几个单项式的和叫作多项式;3、次数:多项式里次数最高的项的次
数叫作这个多项式的次数.2、项:在多项式中每一个单项式叫作
多项式的项,其中不字母的项叫作常数项;用多项式填空,并指出它们的项和次数. (1)温度由t°C下降5°C后是____________; (2)甲数x的 与乙数y的 的差可以表示
为_____; (3)如图,圆环的面积为_______. 一 下列式子中,哪些是单项式?哪些是多项式?哪些是整式?单项式:多项式:整式:(1)多项式 的次数是2 ( )(2)多项式 的一次项系数是1 ( )(3) 是三次三项式 ( )二 判断题:2、多项式的项应包括它前面的符号;多项式没有系数,但每一项都有系数,每一项系也应包括它前面的符号.3、多项式次数与单项式次数不同,但又有联系,首先应求出多项式中各项(单项式)的次数,次数最高的就是这个多项式的次数.4、一个多项式最高次次项不唯一,次高次项也不唯一.1、整式的概念;单项式、多项式以及相关概念. 例:一条河流的水流速为2.5千米/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?如果甲、乙两条船在静水中的速度分别是20千米/时和35千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度分别是多少? 解:设船在静水中的速度是v千米/小时,则
当船顺水行驶时,船的速度为(v+2.5)千米/时.
当船逆水行驶时,船的速度为(v-2.5)千米/时.
若甲船在静水中的速度是20千米/时,即v=20,则
v+2.5=20+2.5=22.5;
v-2.5=20-2.5=17.5.
若乙船在静水中的速度是35千米/时,即v=35,则
v+2.5=35+2.5=37.5;
v-2.5=35-2.5=32.5.
由上可知,甲船顺水行驶的速度是22.5千米/时,逆
水行驶的速度是17.5千米/时;
乙船顺水行驶的速度是37.5千米/时,逆水行驶的速
度是32.5千米/时. 记事:本课按些课件讲时,注意在第八张后讲要向学生介绍整式的概念,及多项式的说法
