11.2.2三角形的外角说课课件
文档属性
| 名称 | 11.2.2三角形的外角说课课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 143.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 00:00:00 | ||
图片预览




文档简介
课件15张PPT。数学说题 广西隆安县南圩镇初级中学
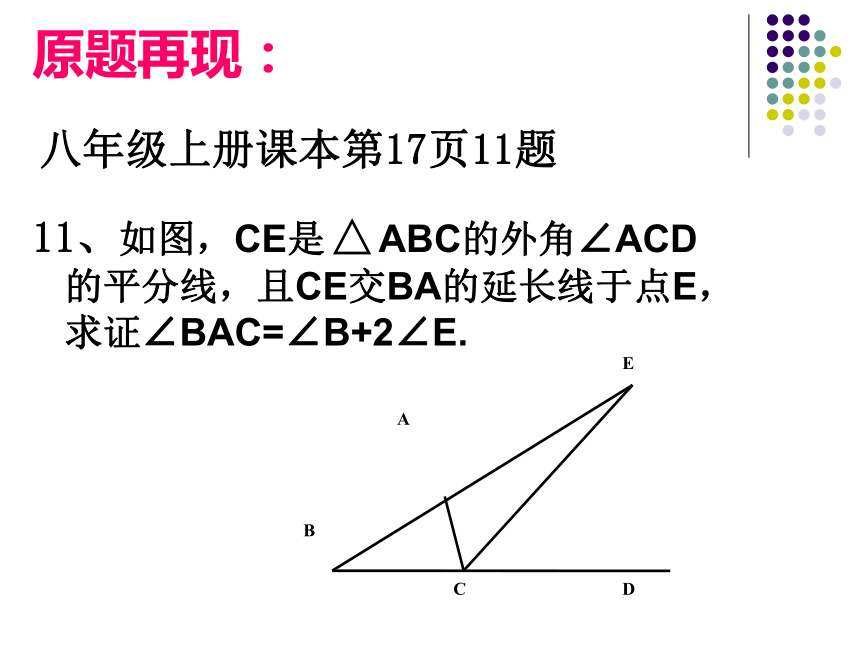
邱 洁 说 题 流 程 背景 题意 解法 变化 反思 教法原题再现:八年级上册课本第17页11题11、如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求证∠BAC=∠B+2∠E. 一、题目的背景: 本题目来自人教版八年级数学上册11.2.2三角形外角的习题11.2第17页11题。本题是关于三角形知识的证明题,放在习题的拓广探索处,目的是考查学生对基础知识的撑握程度,培养学生观察、分析、概括、归纳及数学语言的表达能力。涉及的知识点有:(1)角平分线的概念;(2)三角形外角的概念;(3)三角形内角和定理的推论。用到的数学思想有:数形结合和化归、特殊到一般。 二、题目的意思: 按照编写教材的意图,本题为了巩固角平分线的概念,三角形外角的概念,以及三角形内角和推论的知识综合运用,从而一步熟悉证明的过程。本题求证∠BAC=∠B+2∠E,是一个包含角的数量关系的等式,是一道难度较大的证明题,想要找出突破点,首先得结合图形具体分析∠BAC、∠B、∠E的位置,再由已知条件:∠ACD是 ABC的一个外角和CE是∠ACD的平分线,还有隐含的条件:∠BAC是 ACE的一个外角,再得出结论:∠DCE=∠ACE, ∠DCE=∠B+∠E, ∠BAC=∠ACE+∠E,最后利用等量代换达到求证目的。三、题目的解法: 为了解决本题,先复习角平分线的概念、三角形外角的概念,以及三角形内角和推论的知识。注意引导学生读懂图形,理解题意,运用“执果索因”的方法来指导,从求证出发,和学生一起观察图形,分析等式中各个角的位置。然后结合题目的已知条件,让学生自主探究,进行合作交流,再深入挖掘题目中的隐含条件,从而得出结论,最后完成证明过程。具体过程分析如下: 1、执果: 从求证∠BAC=∠B+2∠E= ∠B+∠E+ ∠E出发,结合图形找出∠BAC、∠B、∠E的位置;
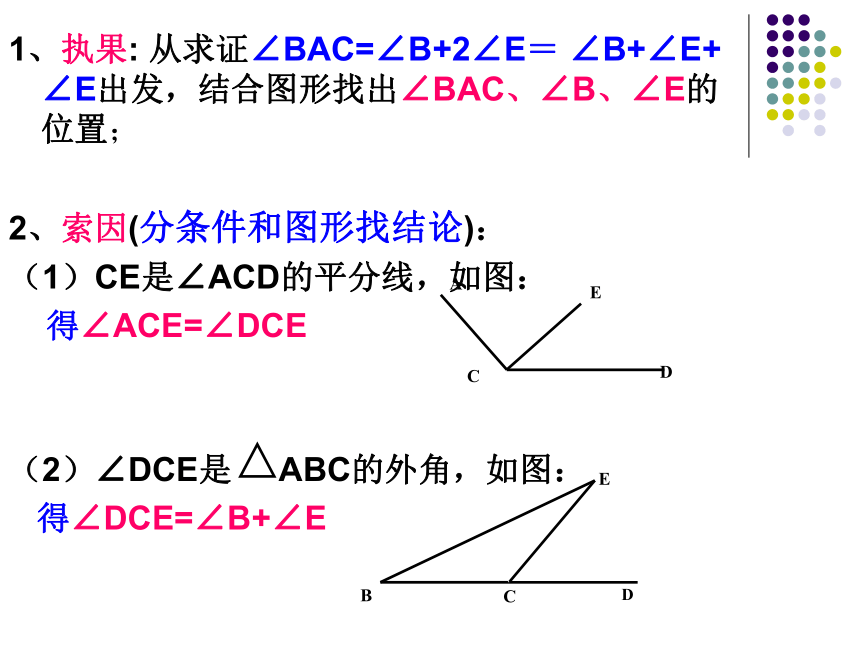
2、索因(分条件和图形找结论):
(1)CE是∠ACD的平分线,如图:
得∠ACE=∠DCE
(2)∠DCE是 ABC的外角,如图:
得∠DCE=∠B+∠ED(3)∠BAC是 ACE的外角,如图:
得 ∠BAC=∠ACE+∠E
3、综合上述等式,分析各个等式中等量代换的关系 :
∠DCE=∠ACE
∠DCE=∠B+∠E
∠BAC=∠ACE+∠E4、整理解答过程:
证明:∵CE是∠ACD的平分线
∴∠DCE=∠ACE
∵∠DCE是 BCE的外角
∴∠DCE=∠B+∠E
∵∠BAC是 ACE的外角
∴∠BAC=∠ACE+∠E
∴∠BAC=∠B+∠E +∠E
即∠BAC=∠B+2∠E四、题目的变化: 本题是关于三角形知识的综合运用,深入挖掘本题的条件和结论,寻找出各个知识间的联系、转化,激发学生爱思考,主动探索的学习积极性,培养学生提问题和分析的能力,同时为了更好地理解题意
1、改变条件和结论为一般求解题:
(1)如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=35°,∠DCE=50°求∠CAE的度数。D(2)如图,CE是 ABC的外角∠ACD的平分线,且CE交∠CBF的平分线于点E,∠E=25°求∠F的度数。
2、改变结论的证明题:
如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求证∠ACE=∠B+∠E.DD 由于学生认知水平有限,为了增强学生学习的信心,上述变化都是在原题的基础上作了一些普通的变式,只要运用与原题相同的方法就可解决。因此解决几何题的方法,只要读懂图形,理解题意,深入挖掘题目中的隐含条件,撑握方法,虽然有些条件或结论的形式,还有图形也发生变化,而其本质特征是没有变化的。五、总结反思: 本题是一道关于角的数量关系的证明题,综合运用三角形的知识点较多,难度较大,鉴于学生学习的知识有限,此题证明方法单一,重在培养推理论证能力和数学语言的表达能力,还有养成书写证明过程的条理性的良好习惯。通过一些变化题目,在于培养思维的灵活性,只要做好引导学生探索数学的解题方法,教会学生思考,善于思考,做一题,通一类,会一片,让学生从题海中解脱出来去畅游更广的知识海洋。六、教法:1、注重形成平等的师生关系,创设浓厚的学习环境,体现教师的引导、组织作用;
2、重视培养学生的自主探索能力,充分调动学生思考积极性,鼓励学生主动合作交流,从而获得广泛的数学知识;
3、能恰当地运用现代教育技术,让数学更具形象,能更好吸引学生的注意力,提高学习兴趣。指导!
邱 洁 说 题 流 程 背景 题意 解法 变化 反思 教法原题再现:八年级上册课本第17页11题11、如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求证∠BAC=∠B+2∠E. 一、题目的背景: 本题目来自人教版八年级数学上册11.2.2三角形外角的习题11.2第17页11题。本题是关于三角形知识的证明题,放在习题的拓广探索处,目的是考查学生对基础知识的撑握程度,培养学生观察、分析、概括、归纳及数学语言的表达能力。涉及的知识点有:(1)角平分线的概念;(2)三角形外角的概念;(3)三角形内角和定理的推论。用到的数学思想有:数形结合和化归、特殊到一般。 二、题目的意思: 按照编写教材的意图,本题为了巩固角平分线的概念,三角形外角的概念,以及三角形内角和推论的知识综合运用,从而一步熟悉证明的过程。本题求证∠BAC=∠B+2∠E,是一个包含角的数量关系的等式,是一道难度较大的证明题,想要找出突破点,首先得结合图形具体分析∠BAC、∠B、∠E的位置,再由已知条件:∠ACD是 ABC的一个外角和CE是∠ACD的平分线,还有隐含的条件:∠BAC是 ACE的一个外角,再得出结论:∠DCE=∠ACE, ∠DCE=∠B+∠E, ∠BAC=∠ACE+∠E,最后利用等量代换达到求证目的。三、题目的解法: 为了解决本题,先复习角平分线的概念、三角形外角的概念,以及三角形内角和推论的知识。注意引导学生读懂图形,理解题意,运用“执果索因”的方法来指导,从求证出发,和学生一起观察图形,分析等式中各个角的位置。然后结合题目的已知条件,让学生自主探究,进行合作交流,再深入挖掘题目中的隐含条件,从而得出结论,最后完成证明过程。具体过程分析如下: 1、执果: 从求证∠BAC=∠B+2∠E= ∠B+∠E+ ∠E出发,结合图形找出∠BAC、∠B、∠E的位置;
2、索因(分条件和图形找结论):
(1)CE是∠ACD的平分线,如图:
得∠ACE=∠DCE
(2)∠DCE是 ABC的外角,如图:
得∠DCE=∠B+∠ED(3)∠BAC是 ACE的外角,如图:
得 ∠BAC=∠ACE+∠E
3、综合上述等式,分析各个等式中等量代换的关系 :
∠DCE=∠ACE
∠DCE=∠B+∠E
∠BAC=∠ACE+∠E4、整理解答过程:
证明:∵CE是∠ACD的平分线
∴∠DCE=∠ACE
∵∠DCE是 BCE的外角
∴∠DCE=∠B+∠E
∵∠BAC是 ACE的外角
∴∠BAC=∠ACE+∠E
∴∠BAC=∠B+∠E +∠E
即∠BAC=∠B+2∠E四、题目的变化: 本题是关于三角形知识的综合运用,深入挖掘本题的条件和结论,寻找出各个知识间的联系、转化,激发学生爱思考,主动探索的学习积极性,培养学生提问题和分析的能力,同时为了更好地理解题意
1、改变条件和结论为一般求解题:
(1)如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=35°,∠DCE=50°求∠CAE的度数。D(2)如图,CE是 ABC的外角∠ACD的平分线,且CE交∠CBF的平分线于点E,∠E=25°求∠F的度数。
2、改变结论的证明题:
如图,CE是 ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求证∠ACE=∠B+∠E.DD 由于学生认知水平有限,为了增强学生学习的信心,上述变化都是在原题的基础上作了一些普通的变式,只要运用与原题相同的方法就可解决。因此解决几何题的方法,只要读懂图形,理解题意,深入挖掘题目中的隐含条件,撑握方法,虽然有些条件或结论的形式,还有图形也发生变化,而其本质特征是没有变化的。五、总结反思: 本题是一道关于角的数量关系的证明题,综合运用三角形的知识点较多,难度较大,鉴于学生学习的知识有限,此题证明方法单一,重在培养推理论证能力和数学语言的表达能力,还有养成书写证明过程的条理性的良好习惯。通过一些变化题目,在于培养思维的灵活性,只要做好引导学生探索数学的解题方法,教会学生思考,善于思考,做一题,通一类,会一片,让学生从题海中解脱出来去畅游更广的知识海洋。六、教法:1、注重形成平等的师生关系,创设浓厚的学习环境,体现教师的引导、组织作用;
2、重视培养学生的自主探索能力,充分调动学生思考积极性,鼓励学生主动合作交流,从而获得广泛的数学知识;
3、能恰当地运用现代教育技术,让数学更具形象,能更好吸引学生的注意力,提高学习兴趣。指导!
