高二周练考试(答案)(江苏省泰州市泰兴市)
文档属性
| 名称 | 高二周练考试(答案)(江苏省泰州市泰兴市) |

|
|
| 格式 | rar | ||
| 文件大小 | 62.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-20 00:00:00 | ||
图片预览


文档简介
高二周练数学试卷(五)
命题人:叶爱斌 2007-10-19
一、选择题
1、在两个袋内,分别装着写有0,1,2,3,4,5六个数字的6张卡片,今从每个袋中各任取一张卡片,则两数之和等于5的概率为(B )
A、 B、 C、 D、
2、a+b>0,ab>0是a>0,b>0的( c )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
3、“y<-1且x>1”是“”成立的( A )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
4、 如图电路中,规定“开关A的闭合”为条件M,“灯泡B亮”为结论N,观察以下图1和图2,可得出的正确结论分别是 ( A )
A、M是N的充分而不必要条件 B、M是N的必要而不充分条件
C、M是N的充要条件 D、M是N的既不充分也必要不条件
5、在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的,且样本容量为160,则中间一组的频数为( A )
A、32 B、0.2 C、40 D、0.25
6、有下列说法:
⑴一个真命题的逆否命题为真
⑵一个假命题的否命题为真
⑶一个命题的否命题为真,则这个命题不一定为真
⑷一个命题的逆命题为真,则这个命题的否命题一定为真
其中,正确的说法有( C )
A、1 B、2 C、3 D、4
7.设原命题:若,则 中至少有一个不小于,则原命题与其逆命题的真假情况是( A )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
8、在长为10 cm的线段AB上任取一点C,并以线段AC为边作正方形,这个正方形的面积介于25 cm2与49 cm2 之间的概率为( B )
A、 B、 C、 D、
9、考虑一元二次方程x2+mx+n=0,其中m、n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( A )
A、 B、 C、 D、
10.有下列命题:①年月日是国庆节,又是中秋节;②的倍数一定是的倍数;
③梯形不是矩形;④方程的解。其中使用逻辑联结词的命题有( B )
A.个 B.个 C.个 D.个
11.已知条件,条件,则是的( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12、命题甲:成等比数列;命题乙:成等差数列,则
甲是乙的 ( B )
A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分又非必要条件
二、填空题(本大题共6小题,每小题5分,共30分,答案须填在题中横线上)
13、 某城市有学校700所,其中大学20所,中学200所,小学480所.现用分层抽样的方法从中抽取一个容量为70的样本进行某项调查,则应抽取的中学数为 20 。
14、 从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是 1/3 。
15、 已知样本的平均数是,标准差是,则 96 。
16、方程3x2-10x+k=0(k∈R)有相异的两个同号实根的充要条件是 (0 , 25/3) 。
17、有一个圆内接正三角形,随机向圆面上投一镖中圆面,那么镖落在三角形内的概率为_____ _______。
18、设甲袋装有m个白球,n个黑球,乙袋装有m个黑球,n个白球,从甲、乙袋中各摸一球.设事件A:“两球相同”,事件B:“两球异色”,则P(A) 与P(B)的大小是 。
解:基本事件总数为(m+n)2,“两球同色”可分为“两球皆白”或“两球皆黑”,则P(A)=,“两球异色”可分为“一白一黑”或“一黑一白”,则P(B)=.
∵P(B)-P(A)=≥0,
∴P(A)≤P(B),当且仅当“m=n”时取等号.
三、解答题(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)
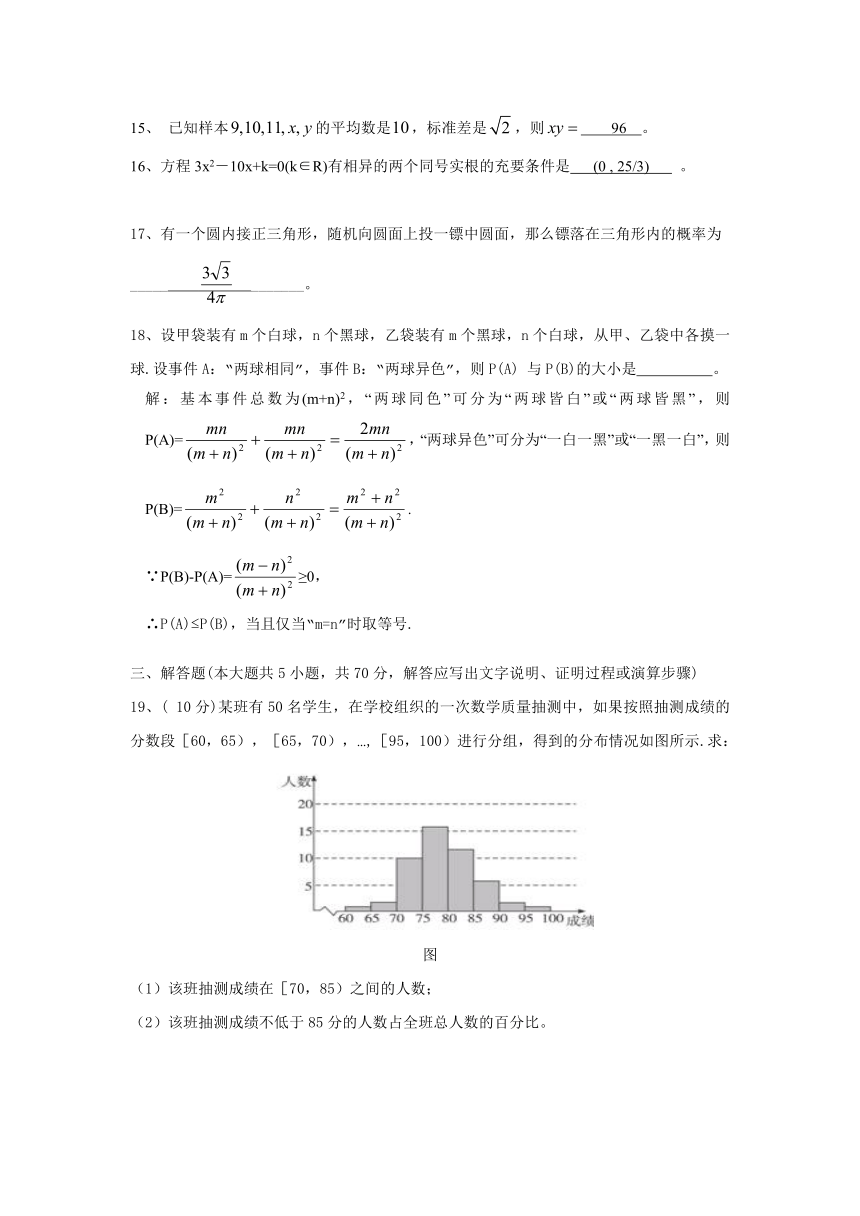
19、( 10分)某班有50名学生,在学校组织的一次数学质量抽测中,如果按照抽测成绩的分数段[60,65),[65,70),…,[95,100)进行分组,得到的分布情况如图所示.求:
图
(1)该班抽测成绩在[70,85)之间的人数;
(2)该班抽测成绩不低于85分的人数占全班总人数的百分比。
解:从分布图可以看出,抽测成绩各分数段的人数依次为:
[60,65)1人;[65,70)2人;[70,75)10人;[75,80)16人;[80,85)12人;[85,90)6人;[90,95)2人;[95,100)1人.因此,
(1)该班抽测成绩在[70,85)之间的人数为38人.
(2)该班抽测成绩不低于85分的占总人数的18%.
20、(10分)设x,yR,求证:|x+y|=|x|+|y|成立的充要条件是xy0
21、(12分)已知,且p是q必要不充分条件,求实数m的取值范围。
解: (-1,9)
22、(12分) 已知方程求使方程有两个大于1的实数根的充要条件,并写出它的一个必要不充分条件。
解:分析:△是方程有实数根的充要条件,但只是方程有两个大于1的实数根的必要非充分条件。因此还需结合实根大于1的性质寻求条件组。
解:当△=时,方程有两个实数根 ,
所以,方程有两个大于1的实数根的充要条件为:
解(1),得;解(2),得。
解(3),得 ;解(4),得,即或。
综合(1),(3),(4)得。
方程有两个大于1的实数根的充要条件是。
23、(本题满分12分)设有关于的一元二次方程.
(1)若是从四个数中任取的一个数,是从任取的一个数,求上述方程有实根的概率.
(2)若是从区间任取的一个数, 是从区间任取的一个数,求上述方程有实根的概率.
解:设事件为“方程有实根”
当,时,方程有实根的充要条件为
(Ⅰ)基本事件共12个:
,其中第一个数表示的取值,第二个数表示的取值
事件A中包含9个基本事件,事件A发生的概率为
(Ⅱ)试验的全部结束所构成的区域为
构成事件的区域为
所以所求的概率为
24、(本小题满分14分)
将一颗骰子先后抛掷2次,观察向上的点数,问:
(1)两数之和为8的概率;
(2)两数之和是3的倍数的概率;
(3)两数之积是6的倍数的概率。
(4)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=25的内部的概率。
解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件
(1)记“两数之和为6”为事件A,则事件A中含有5个基本事件,所以
P(A)=;
答:两数之和为6的概率为。
(2)记“两数之和是3的倍数”为事件B,则事件B中含有12个基本事件,所以
P(B)=;
答:两数之和是3的倍数的概率为。
(3)记“向上的两数之积是6的倍数”为事件C,则事件C中含有其中的15个等可能基本事件,所以
P(C)=,
答:两数之积是6的倍数的概率为。
(4)基本事件总数为36,点(x,y),在圆x2+y2=25的内部记为事件D,则D包含13个事件,
所以P(D)=。
答:点(x,y)在圆x2+y2=25的内部的概率。
命题人:叶爱斌 2007-10-19
一、选择题
1、在两个袋内,分别装着写有0,1,2,3,4,5六个数字的6张卡片,今从每个袋中各任取一张卡片,则两数之和等于5的概率为(B )
A、 B、 C、 D、
2、a+b>0,ab>0是a>0,b>0的( c )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
3、“y<-1且x>1”是“”成立的( A )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
4、 如图电路中,规定“开关A的闭合”为条件M,“灯泡B亮”为结论N,观察以下图1和图2,可得出的正确结论分别是 ( A )
A、M是N的充分而不必要条件 B、M是N的必要而不充分条件
C、M是N的充要条件 D、M是N的既不充分也必要不条件
5、在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的,且样本容量为160,则中间一组的频数为( A )
A、32 B、0.2 C、40 D、0.25
6、有下列说法:
⑴一个真命题的逆否命题为真
⑵一个假命题的否命题为真
⑶一个命题的否命题为真,则这个命题不一定为真
⑷一个命题的逆命题为真,则这个命题的否命题一定为真
其中,正确的说法有( C )
A、1 B、2 C、3 D、4
7.设原命题:若,则 中至少有一个不小于,则原命题与其逆命题的真假情况是( A )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
8、在长为10 cm的线段AB上任取一点C,并以线段AC为边作正方形,这个正方形的面积介于25 cm2与49 cm2 之间的概率为( B )
A、 B、 C、 D、
9、考虑一元二次方程x2+mx+n=0,其中m、n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( A )
A、 B、 C、 D、
10.有下列命题:①年月日是国庆节,又是中秋节;②的倍数一定是的倍数;
③梯形不是矩形;④方程的解。其中使用逻辑联结词的命题有( B )
A.个 B.个 C.个 D.个
11.已知条件,条件,则是的( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12、命题甲:成等比数列;命题乙:成等差数列,则
甲是乙的 ( B )
A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分又非必要条件
二、填空题(本大题共6小题,每小题5分,共30分,答案须填在题中横线上)
13、 某城市有学校700所,其中大学20所,中学200所,小学480所.现用分层抽样的方法从中抽取一个容量为70的样本进行某项调查,则应抽取的中学数为 20 。
14、 从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是 1/3 。
15、 已知样本的平均数是,标准差是,则 96 。
16、方程3x2-10x+k=0(k∈R)有相异的两个同号实根的充要条件是 (0 , 25/3) 。
17、有一个圆内接正三角形,随机向圆面上投一镖中圆面,那么镖落在三角形内的概率为_____ _______。
18、设甲袋装有m个白球,n个黑球,乙袋装有m个黑球,n个白球,从甲、乙袋中各摸一球.设事件A:“两球相同”,事件B:“两球异色”,则P(A) 与P(B)的大小是 。
解:基本事件总数为(m+n)2,“两球同色”可分为“两球皆白”或“两球皆黑”,则P(A)=,“两球异色”可分为“一白一黑”或“一黑一白”,则P(B)=.
∵P(B)-P(A)=≥0,
∴P(A)≤P(B),当且仅当“m=n”时取等号.
三、解答题(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)
19、( 10分)某班有50名学生,在学校组织的一次数学质量抽测中,如果按照抽测成绩的分数段[60,65),[65,70),…,[95,100)进行分组,得到的分布情况如图所示.求:
图
(1)该班抽测成绩在[70,85)之间的人数;
(2)该班抽测成绩不低于85分的人数占全班总人数的百分比。
解:从分布图可以看出,抽测成绩各分数段的人数依次为:
[60,65)1人;[65,70)2人;[70,75)10人;[75,80)16人;[80,85)12人;[85,90)6人;[90,95)2人;[95,100)1人.因此,
(1)该班抽测成绩在[70,85)之间的人数为38人.
(2)该班抽测成绩不低于85分的占总人数的18%.
20、(10分)设x,yR,求证:|x+y|=|x|+|y|成立的充要条件是xy0
21、(12分)已知,且p是q必要不充分条件,求实数m的取值范围。
解: (-1,9)
22、(12分) 已知方程求使方程有两个大于1的实数根的充要条件,并写出它的一个必要不充分条件。
解:分析:△是方程有实数根的充要条件,但只是方程有两个大于1的实数根的必要非充分条件。因此还需结合实根大于1的性质寻求条件组。
解:当△=时,方程有两个实数根 ,
所以,方程有两个大于1的实数根的充要条件为:
解(1),得;解(2),得。
解(3),得 ;解(4),得,即或。
综合(1),(3),(4)得。
方程有两个大于1的实数根的充要条件是。
23、(本题满分12分)设有关于的一元二次方程.
(1)若是从四个数中任取的一个数,是从任取的一个数,求上述方程有实根的概率.
(2)若是从区间任取的一个数, 是从区间任取的一个数,求上述方程有实根的概率.
解:设事件为“方程有实根”
当,时,方程有实根的充要条件为
(Ⅰ)基本事件共12个:
,其中第一个数表示的取值,第二个数表示的取值
事件A中包含9个基本事件,事件A发生的概率为
(Ⅱ)试验的全部结束所构成的区域为
构成事件的区域为
所以所求的概率为
24、(本小题满分14分)
将一颗骰子先后抛掷2次,观察向上的点数,问:
(1)两数之和为8的概率;
(2)两数之和是3的倍数的概率;
(3)两数之积是6的倍数的概率。
(4)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=25的内部的概率。
解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件
(1)记“两数之和为6”为事件A,则事件A中含有5个基本事件,所以
P(A)=;
答:两数之和为6的概率为。
(2)记“两数之和是3的倍数”为事件B,则事件B中含有12个基本事件,所以
P(B)=;
答:两数之和是3的倍数的概率为。
(3)记“向上的两数之积是6的倍数”为事件C,则事件C中含有其中的15个等可能基本事件,所以
P(C)=,
答:两数之积是6的倍数的概率为。
(4)基本事件总数为36,点(x,y),在圆x2+y2=25的内部记为事件D,则D包含13个事件,
所以P(D)=。
答:点(x,y)在圆x2+y2=25的内部的概率。
