2023-2024学年北师大版数学七年级上册 5.4应用一元一次方程——打折销售【素养基础达标】(含解析)
文档属性
| 名称 | 2023-2024学年北师大版数学七年级上册 5.4应用一元一次方程——打折销售【素养基础达标】(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览



文档简介
5.4应用一元一次方程——打折销售
【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
8由实际问题抽象出一元一次方程
审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.
(1)“总量=各部分量的和”是列方程解应用题中一个基本的关系式,在这一类问题中,表示出各部分的量和总量,然后利用它们之间的等量关系列方程.
(2)“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.通过对同一个量从不同的角度用不同的式子表示,进而列出方程.
一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价-进价,;
(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
6.(检验)
素养基础达标
一.选择题(共10小题)
1.把这9个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图,是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中的值为
A.1 B.3 C.4 D.6
2.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中《均输》卷记载了一道有趣的数学问题:“今有凫(注释:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”译文:“野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.现野鸭与大雁分别从南海和北海同时起飞,问经过多少天相遇.”设野鸭与大雁经过天相遇,根据题意,下面所列方程正确的是
A. B. C. D.
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?若设井深为尺,则下面所列方程正确的是
A. B.
C. D.
4.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人6两,还剩3两;若每人8两,还差4两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
5.《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?
译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发日,甲乙相逢,可列方程
A. B. C. D.
6.某商品的标价为126元,若降价以九五折出售(优惠仍可获利(相对于进货价)则该商品的进货价是
A.114元 B.113.4元 C.119.7元 D.112元
7.一件夹克衫先按成本提高标价,再以8折出售,获利28元.这件夹克衫的成本是
A.210元 B.28元 C.168元 D.140元
8.某品牌奶茶进行促销活动,优惠措施是“第二杯半价”.现购买两杯该品牌奶茶,这两杯奶茶共打了
A.7折 B.7.5折 C.8折 D.8.5折
9.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送20件,还剩12件;若每个快递员派送24件,还差12件,设该分派站有名快递员,则可列方程为
A. B.
C. D.
10.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
二.填空题(共6小题)
11.现在是6点,至少经过 分钟,分针与时针互相垂直.
12.用150张白铁皮做罐头盒,每张白铁皮可制盒身15个或盒底41个,一个盒身与两个盒底配成一套罐头盒.设把张白铁皮制盒身,则可列方程为 .
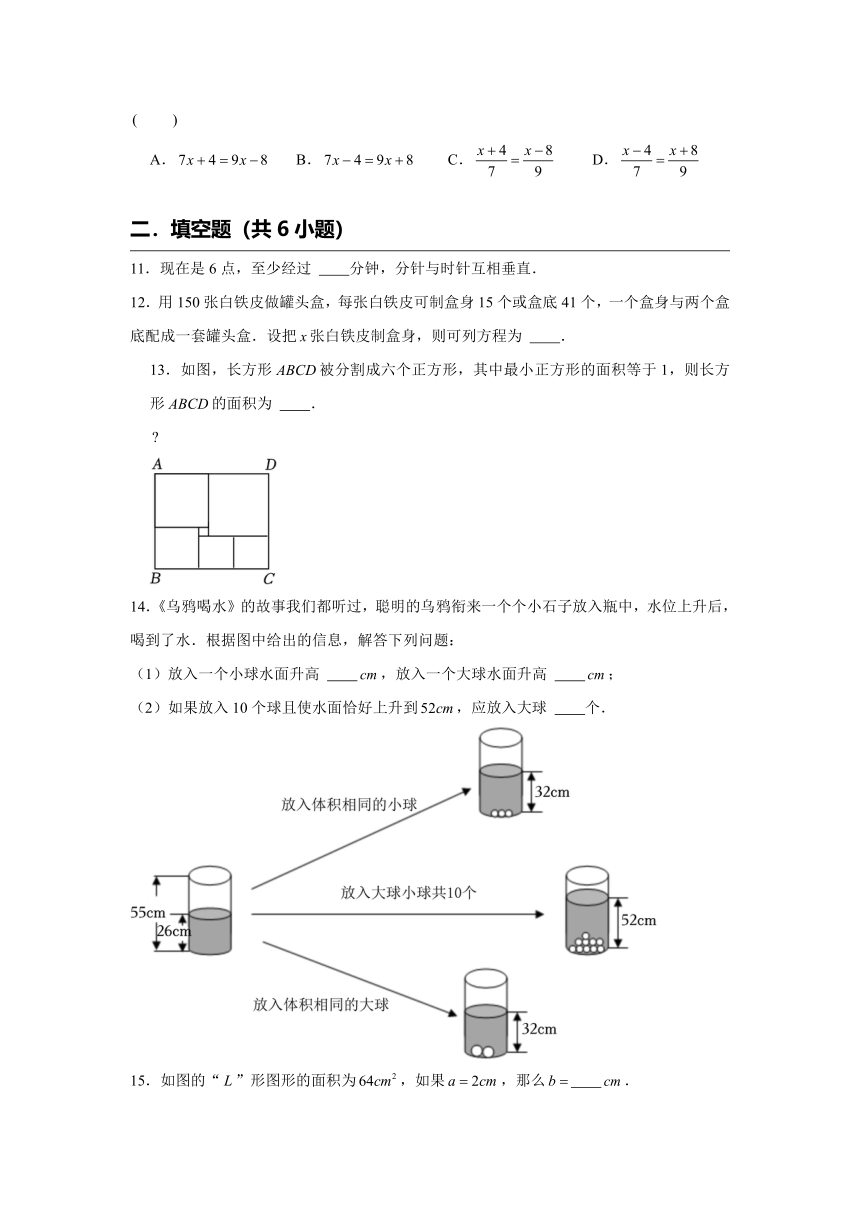
13.如图,长方形被分割成六个正方形,其中最小正方形的面积等于1,则长方形的面积为 .
14.《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 ,放入一个大球水面升高 ;
(2)如果放入10个球且使水面恰好上升到,应放入大球 个.
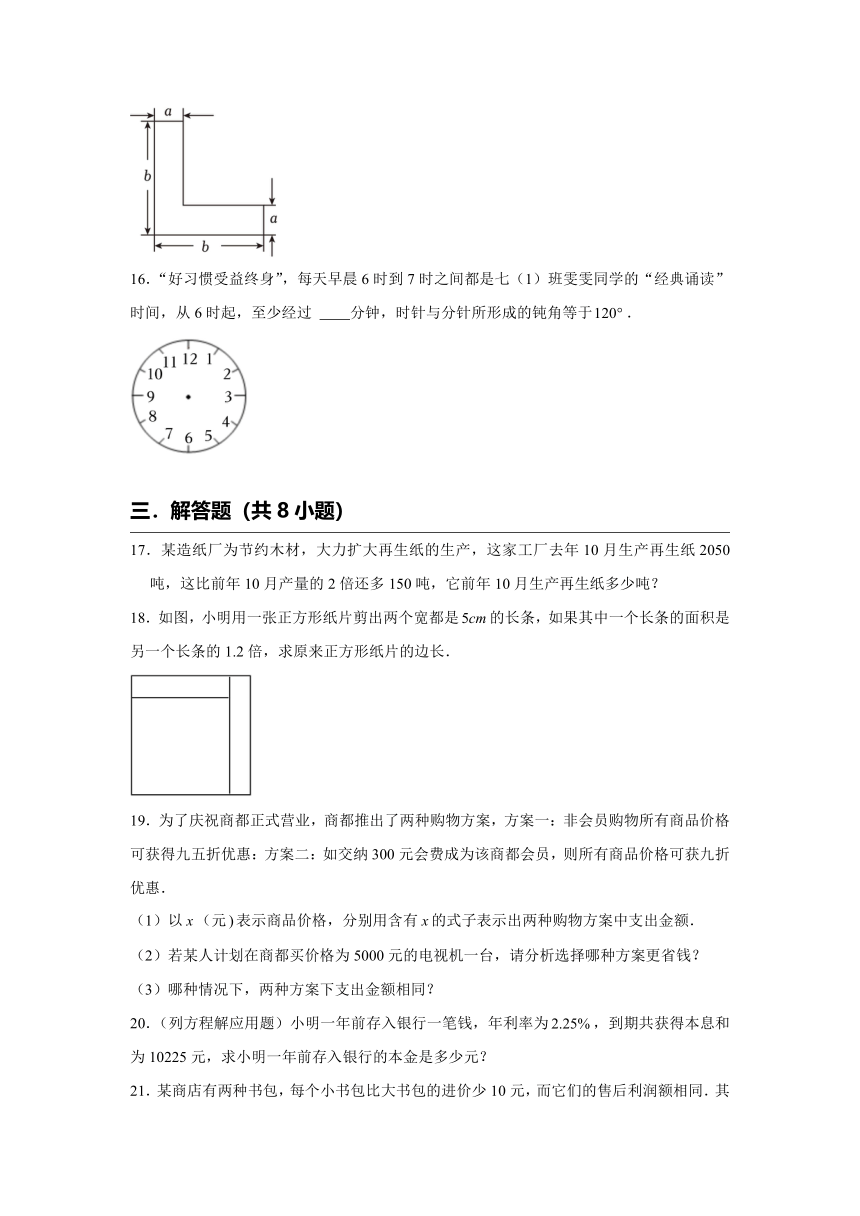
15.如图的“”形图形的面积为,如果,那么 .
16.“好习惯受益终身”,每天早晨6时到7时之间都是七(1)班雯雯同学的“经典诵读”时间,从6时起,至少经过 分钟,时针与分针所形成的钝角等于.
三.解答题(共8小题)
17.某造纸厂为节约木材,大力扩大再生纸的生产,这家工厂去年10月生产再生纸2050吨,这比前年10月产量的2倍还多150吨,它前年10月生产再生纸多少吨?
18.如图,小明用一张正方形纸片剪出两个宽都是的长条,如果其中一个长条的面积是另一个长条的1.2倍,求原来正方形纸片的边长.
19.为了庆祝商都正式营业,商都推出了两种购物方案,方案一:非会员购物所有商品价格可获得九五折优惠:方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额.
(2)若某人计划在商都买价格为5000元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案下支出金额相同?
20.(列方程解应用题)小明一年前存入银行一笔钱,年利率为,到期共获得本息和为10225元,求小明一年前存入银行的本金是多少元?
21.某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为,每个大书包的盈利率为,试求两种书包的进价.
22.在学习《水箱变高了》一课时,张老师将一个半径,高的圆柱形橡皮泥模型,重新揉成一个半径为的圆柱形,此时圆柱形的高为多少呢?
(1)请画出变形前后模型的示意图,并在示意图上标注对应的已知数据;
(2)通过列方程求变形后模型的高.
23.某市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天.问这项工程一共用了多少天?
24.七年级(1)班在召开期末总结表彰会前,班主任安排班长去商店买奖品,下面是班长与售货员的对话:
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
5.4应用一元一次方程——打折销售
【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
8由实际问题抽象出一元一次方程
审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.
(1)“总量=各部分量的和”是列方程解应用题中一个基本的关系式,在这一类问题中,表示出各部分的量和总量,然后利用它们之间的等量关系列方程.
(2)“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.通过对同一个量从不同的角度用不同的式子表示,进而列出方程.
一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价-进价,;
(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
6.(检验)
素养基础达标
一.选择题(共10小题)
1.把这9个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图,是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中的值为
A.1 B.3 C.4 D.6
【答案】
【分析】根据任意一行,任意一列及两条对角线上的数之和都相等,可得第三行与第三列上的两个数之和相等,依此列出方程即可.
【解答】解:由题意,可得:,
解得:.
故选:.
2.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中《均输》卷记载了一道有趣的数学问题:“今有凫(注释:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”译文:“野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.现野鸭与大雁分别从南海和北海同时起飞,问经过多少天相遇.”设野鸭与大雁经过天相遇,根据题意,下面所列方程正确的是
A. B. C. D.
【分析】设野鸭与大雁经过天相遇,南海和北海之间的路程为1,则野鸭每天飞行,大雁每天飞行,根据野鸭和大雁路程和等于1,即可得出关于的一元一次方程,此题得解.
【解答】解:设野鸭与大雁经过天相遇,
根据题意得:.
故选:.
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?若设井深为尺,则下面所列方程正确的是
A. B.
C. D.
【答案】
【分析】根据绳子的长度不变,即可得出关于的一元一次方程,此题得解.
【解答】解:用绳子量井深,把绳三折来量,井外余绳四尺,
绳子的长度为尺;
又用绳子量井深,把绳四折来量,井外余绳一尺,
绳子的长度为尺.
根据题意可列出方程.
故选:.
4.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人6两,还剩3两;若每人8两,还差4两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
【答案】
【分析】根据“每人6两,还剩3两;每人8两,还差4两”,结合银子的总数不变,即可得出关于的一元一次方程,此题得解.
【解答】解:根据题意得,
故选:.
5.《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?
译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发日,甲乙相逢,可列方程
A. B. C. D.
【答案】
【分析】根据题意设甲乙经过日相逢,则甲、乙分别所走路程占总路程的和,进而得出等式.
【解答】解:设甲乙经过日相逢,可列方程:
.
故选:.
6.某商品的标价为126元,若降价以九五折出售(优惠仍可获利(相对于进货价)则该商品的进货价是
A.114元 B.113.4元 C.119.7元 D.112元
【答案】
【分析】根据利润标价进价计算即可.
【解答】解:设商品的进货价是元,
根据题意,得,
解得,
故选:.
7.一件夹克衫先按成本提高标价,再以8折出售,获利28元.这件夹克衫的成本是
A.210元 B.28元 C.168元 D.140元
【答案】
【分析】设这件夹克衫的成本为元,然后根据获利28元列出等式即可求出答案.
【解答】解:设这件夹克衫的成本为元,
,
解得:,
故选:.
8.某品牌奶茶进行促销活动,优惠措施是“第二杯半价”.现购买两杯该品牌奶茶,这两杯奶茶共打了
A.7折 B.7.5折 C.8折 D.8.5折
【答案】
【分析】设第一杯奶茶为元,则第二杯奶茶元,根据两杯奶茶的现价除以两杯奶茶的原价等于折扣率,列出代数式,计算即可得到结果.
【解答】解:设第一杯奶茶为元,则第二杯奶茶元,
由题意得:,
这两杯奶茶共打了7.5折.
故选:.
9.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送20件,还剩12件;若每个快递员派送24件,还差12件,设该分派站有名快递员,则可列方程为
A. B.
C. D.
【答案】
【分析】设该分派站有个快递员,根据“每个快递员派送20件,还剩12件;若每个快递员派送24件,还差12件”,即可得出关于的一元一次方程.
【解答】解:设该分派站有名快递员,则可列方程为:.
故选:.
10.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
【答案】
【分析】根据“每人7两,还剩4两;每人9两,还差8两”,结合分银子的人数不变,即可得出关于的一元一次方程,此题得解.
【解答】解:银子共有两,每人7两,还剩4两,
分银子的人共人;
银子共有两,每人9两,还差8两,
分银子的人共人.
又分银子的人数不变,
可列方程组.
故选:.
二.填空题(共6小题)
11.现在是6点,至少经过 分钟,分针与时针互相垂直.
【答案】.
【分析】设再经过分钟,分针与时针互相垂直,根据角度差列出方程,解之即可.
【解答】解:6点整时,分钟与时针的夹角为,
设再经过分钟,分针与时针互相垂直,
则分针转了,时针转了,
由已知得:,
解得:,
故答案为:.
12.用150张白铁皮做罐头盒,每张白铁皮可制盒身15个或盒底41个,一个盒身与两个盒底配成一套罐头盒.设把张白铁皮制盒身,则可列方程为 .
【答案】.
【分析】设把张白铁皮制盒身,则张白铁皮制盒底,根据“一个盒身与两个盒底配成一套罐头盒”列出一元一次方程即可求解.
【解答】解:设把张白铁皮制盒身,则张白铁皮制盒底,根据题意得,
,
故答案为:.
13.如图,长方形被分割成六个正方形,其中最小正方形的面积等于1,则长方形的面积为 143 .
【答案】143.
【分析】给图中各正方形标上序号,设正方形4的边长为,则正方形3的边长为,正方形2的边长为,正方形1的边长为或,由正方形1的边长不变,可得出关于的一元一次方程,解之可得出的值,再将其代入中,即可求出结论.
【解答】解:给图中各正方形标上序号,如图所示
设正方形4的边长为,则正方形3的边长为,正方形2的边长为,正方形1的边长为或,
根据题意得:,
解得:,
,
长方形的面积为143.
故答案为:143.
14.《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 2 ,放入一个大球水面升高 ;
(2)如果放入10个球且使水面恰好上升到,应放入大球 个.
【答案】(1)2;3;
(2)6.
【分析】(1)利用放入一个小球水面上升高度放入小球的个数,可求出放入一个小球水面升高;利用放入一个大球水面上升高度放入大球的个数,可求出放入一个大球水面升高;
(2)设应放入个大球,则放入小球,利用水面上升的高度放入大球的个数放入小球的个数,可得出关于的一元一次方程,解之即可得出结论.
【解答】解:(1)根据题意得:放入一个小球水面升高;
放入一个大球水面升高.
故答案为:2;3;
(2)设应放入个大球,则放入小球,
根据题意得:,
解得:,
应放入大球6个.
故答案为:6.
15.如图的“”形图形的面积为,如果,那么 17 .
【答案】17.
【分析】将图形分成两个长方形,根据图形的面积建立方程,解方程即可得到答案.
【解答】解:如图所示,添加辅助线将图形分成两个长方形,
根据题意可得,
,
,
,
,
故答案为:17.
16.“好习惯受益终身”,每天早晨6时到7时之间都是七(1)班雯雯同学的“经典诵读”时间,从6时起,至少经过 分钟,时针与分针所形成的钝角等于.
【答案】.
【分析】先求出经过一分钟时针和分针分别转动的角度,设至少经过分钟,时针与分针所形成的钝角等于,再根据角的和差列出方程,求解即可.
【解答】解:经过一分针,分针转动的角度为:,时针转动的角度为:,
设至少经过分钟,时针与分针所形成的钝角等于,
由题意得:,
解得:,
设至少经过分钟,时针与分针所形成的钝角等于.
故答案为:.
三.解答题(共8小题)
17.某造纸厂为节约木材,大力扩大再生纸的生产,这家工厂去年10月生产再生纸2050吨,这比前年10月产量的2倍还多150吨,它前年10月生产再生纸多少吨?
【分析】设前年10月生产再生纸吨,则去年生产吨,从而可得方程,解出即可.
【解答】解:设前年10月生产再生纸吨,则去年生产吨,
由题意,得:,
解得:.
答:它前年10月生产再生纸950吨.
18.如图,小明用一张正方形纸片剪出两个宽都是的长条,如果其中一个长条的面积是另一个长条的1.2倍,求原来正方形纸片的边长.
【答案】.
【分析】设小长条的长为,则原来正方形的边长为,然后计算两个长条的面积,再利用面积关系列出方程求,即可求出原正方形的边长.
【解答】解:设小长条的长为,则原来正方形的边长为,
小长条的面积为:,大长条的面积为:,
其中一个长条的面积是另一个长条的1.2倍,
,
解得:,
原来正方形纸片的边长为.
故原来正方形纸片的边长为.
19.为了庆祝商都正式营业,商都推出了两种购物方案,方案一:非会员购物所有商品价格可获得九五折优惠:方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额.
(2)若某人计划在商都买价格为5000元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案下支出金额相同?
【答案】(1)方案一支出金额:元,方案二支出金额:元;
(2)买价格为5000元的电视机,选择方案一更省钱;
(3)商品价格为6000元时,两种方案下支出金额相同.
【分析】(1)由已知直接可得答案;
(2)分别计算出商品价格为5000元时,两种方案支付的金额,再比较即可;
(3)根据金额相同列出方程,即可解得答案.
【解答】解:(1)方案一支出金额:元,
方案二支出金额:元;
(2)买价格为5000元的电视机,
方案一支出金额:(元,
方案二支出金额:(元;
,
选择方案一更省钱;
(3)根据题意得:
,
解得,
答:商品价格为6000元时,两种方案下支出金额相同.
20.(列方程解应用题)小明一年前存入银行一笔钱,年利率为,到期共获得本息和为10225元,求小明一年前存入银行的本金是多少元?
【答案】10000元.
【分析】设小明一年前存入银行的本金是元,根据到期共获得本息和为10225元,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设小明一年前存入银行的本金是元,
依题意得:,
解得:.
答:小明一年前存入银行的本金是10000元.
21.某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为,每个大书包的盈利率为,试求两种书包的进价.
【分析】设每个小书包的进价为元,则每个大书包的进价为元,根据利润进价盈利率结合两种书包的售后利润额相同,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设每个小书包的进价为元,则每个大书包的进价为元,
依题意,得:,
解得:,
.
答:每个小书包的进价为20元,每个大书包的进价为30元.
22.在学习《水箱变高了》一课时,张老师将一个半径,高的圆柱形橡皮泥模型,重新揉成一个半径为的圆柱形,此时圆柱形的高为多少呢?
(1)请画出变形前后模型的示意图,并在示意图上标注对应的已知数据;
(2)通过列方程求变形后模型的高.
【答案】(1)画示意图见解答过程;
(2)变形后模型的高为.
【分析】(1)根据题意画出图形即可.
(2)设变形后模型的高为,根据变形前后模型的体积不变列方程即可解得答案.
【解答】解:(1)如图:
(2)设变形后模型的高为,
根据题意得:,
解得,
答:变形后模型的高为.
23.某市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天.问这项工程一共用了多少天?
【答案】9天.
【分析】设这项工程一共用了天,则甲工程队改造了天,乙工程队改造了天,根据甲工程队完成的改造任务量乙工程队完成的改造任务量整个改造任务量,即可得出关于的一元一次方程,解之即可求出这项工程所用时间.
【解答】解:设这项工程一共用了天,则甲工程队改造了天,乙工程队改造了天,
依题意得:,
解得:.
答:这项工程一共用了9天.
24.七年级(1)班在召开期末总结表彰会前,班主任安排班长去商店买奖品,下面是班长与售货员的对话:
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
【分析】设笔记本的单价为元,则钢笔的单价为元,根据总价单价数量,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设笔记本的单价为元,则钢笔的单价为元,
依题意,得:,
解得:,
.
答:笔记本的单价为3元,钢笔的单价为5元.
【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
8由实际问题抽象出一元一次方程
审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.
(1)“总量=各部分量的和”是列方程解应用题中一个基本的关系式,在这一类问题中,表示出各部分的量和总量,然后利用它们之间的等量关系列方程.
(2)“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.通过对同一个量从不同的角度用不同的式子表示,进而列出方程.
一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价-进价,;
(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
6.(检验)
素养基础达标
一.选择题(共10小题)
1.把这9个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图,是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中的值为
A.1 B.3 C.4 D.6
2.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中《均输》卷记载了一道有趣的数学问题:“今有凫(注释:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”译文:“野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.现野鸭与大雁分别从南海和北海同时起飞,问经过多少天相遇.”设野鸭与大雁经过天相遇,根据题意,下面所列方程正确的是
A. B. C. D.
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?若设井深为尺,则下面所列方程正确的是
A. B.
C. D.
4.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人6两,还剩3两;若每人8两,还差4两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
5.《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?
译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发日,甲乙相逢,可列方程
A. B. C. D.
6.某商品的标价为126元,若降价以九五折出售(优惠仍可获利(相对于进货价)则该商品的进货价是
A.114元 B.113.4元 C.119.7元 D.112元
7.一件夹克衫先按成本提高标价,再以8折出售,获利28元.这件夹克衫的成本是
A.210元 B.28元 C.168元 D.140元
8.某品牌奶茶进行促销活动,优惠措施是“第二杯半价”.现购买两杯该品牌奶茶,这两杯奶茶共打了
A.7折 B.7.5折 C.8折 D.8.5折
9.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送20件,还剩12件;若每个快递员派送24件,还差12件,设该分派站有名快递员,则可列方程为
A. B.
C. D.
10.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
二.填空题(共6小题)
11.现在是6点,至少经过 分钟,分针与时针互相垂直.
12.用150张白铁皮做罐头盒,每张白铁皮可制盒身15个或盒底41个,一个盒身与两个盒底配成一套罐头盒.设把张白铁皮制盒身,则可列方程为 .
13.如图,长方形被分割成六个正方形,其中最小正方形的面积等于1,则长方形的面积为 .
14.《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 ,放入一个大球水面升高 ;
(2)如果放入10个球且使水面恰好上升到,应放入大球 个.
15.如图的“”形图形的面积为,如果,那么 .
16.“好习惯受益终身”,每天早晨6时到7时之间都是七(1)班雯雯同学的“经典诵读”时间,从6时起,至少经过 分钟,时针与分针所形成的钝角等于.
三.解答题(共8小题)
17.某造纸厂为节约木材,大力扩大再生纸的生产,这家工厂去年10月生产再生纸2050吨,这比前年10月产量的2倍还多150吨,它前年10月生产再生纸多少吨?
18.如图,小明用一张正方形纸片剪出两个宽都是的长条,如果其中一个长条的面积是另一个长条的1.2倍,求原来正方形纸片的边长.
19.为了庆祝商都正式营业,商都推出了两种购物方案,方案一:非会员购物所有商品价格可获得九五折优惠:方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额.
(2)若某人计划在商都买价格为5000元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案下支出金额相同?
20.(列方程解应用题)小明一年前存入银行一笔钱,年利率为,到期共获得本息和为10225元,求小明一年前存入银行的本金是多少元?
21.某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为,每个大书包的盈利率为,试求两种书包的进价.
22.在学习《水箱变高了》一课时,张老师将一个半径,高的圆柱形橡皮泥模型,重新揉成一个半径为的圆柱形,此时圆柱形的高为多少呢?
(1)请画出变形前后模型的示意图,并在示意图上标注对应的已知数据;
(2)通过列方程求变形后模型的高.
23.某市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天.问这项工程一共用了多少天?
24.七年级(1)班在召开期末总结表彰会前,班主任安排班长去商店买奖品,下面是班长与售货员的对话:
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
5.4应用一元一次方程——打折销售
【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
8由实际问题抽象出一元一次方程
审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程.
(1)“总量=各部分量的和”是列方程解应用题中一个基本的关系式,在这一类问题中,表示出各部分的量和总量,然后利用它们之间的等量关系列方程.
(2)“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.通过对同一个量从不同的角度用不同的式子表示,进而列出方程.
一元一次方程的应用
(一)一元一次方程解应用题的类型有:
(1)探索规律型问题;
(2)数字问题;
(3)销售问题(利润=售价-进价,;
(4)工程问题(①工作量=人均效率×人数×时间;②如果一件工作分几个阶段完成,那么各阶段的工作量的和=工作总量);
(5)行程问题(路程=速度×时间);
(6)等值变换问题;
(7)和,差,倍,分问题;
(8)分配问题;
(9)比赛积分问题;
(10)水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度).
(二)利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.
列一元一次方程解应用题的五个步骤
1.审:仔细审题,确定已知量和未知量,找出它们之间的等量关系.
2.设:设未知数(x),根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数.
3.列:根据等量关系列出方程.
4.解:解方程,求得未知数的值.
5.答:检验未知数的值是否正确,是否符合题意,完整地写出答句.
6.(检验)
素养基础达标
一.选择题(共10小题)
1.把这9个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图,是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则其中的值为
A.1 B.3 C.4 D.6
【答案】
【分析】根据任意一行,任意一列及两条对角线上的数之和都相等,可得第三行与第三列上的两个数之和相等,依此列出方程即可.
【解答】解:由题意,可得:,
解得:.
故选:.
2.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中《均输》卷记载了一道有趣的数学问题:“今有凫(注释:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”译文:“野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.现野鸭与大雁分别从南海和北海同时起飞,问经过多少天相遇.”设野鸭与大雁经过天相遇,根据题意,下面所列方程正确的是
A. B. C. D.
【分析】设野鸭与大雁经过天相遇,南海和北海之间的路程为1,则野鸭每天飞行,大雁每天飞行,根据野鸭和大雁路程和等于1,即可得出关于的一元一次方程,此题得解.
【解答】解:设野鸭与大雁经过天相遇,
根据题意得:.
故选:.
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?若设井深为尺,则下面所列方程正确的是
A. B.
C. D.
【答案】
【分析】根据绳子的长度不变,即可得出关于的一元一次方程,此题得解.
【解答】解:用绳子量井深,把绳三折来量,井外余绳四尺,
绳子的长度为尺;
又用绳子量井深,把绳四折来量,井外余绳一尺,
绳子的长度为尺.
根据题意可列出方程.
故选:.
4.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人6两,还剩3两;若每人8两,还差4两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
【答案】
【分析】根据“每人6两,还剩3两;每人8两,还差4两”,结合银子的总数不变,即可得出关于的一元一次方程,此题得解.
【解答】解:根据题意得,
故选:.
5.《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?
译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发日,甲乙相逢,可列方程
A. B. C. D.
【答案】
【分析】根据题意设甲乙经过日相逢,则甲、乙分别所走路程占总路程的和,进而得出等式.
【解答】解:设甲乙经过日相逢,可列方程:
.
故选:.
6.某商品的标价为126元,若降价以九五折出售(优惠仍可获利(相对于进货价)则该商品的进货价是
A.114元 B.113.4元 C.119.7元 D.112元
【答案】
【分析】根据利润标价进价计算即可.
【解答】解:设商品的进货价是元,
根据题意,得,
解得,
故选:.
7.一件夹克衫先按成本提高标价,再以8折出售,获利28元.这件夹克衫的成本是
A.210元 B.28元 C.168元 D.140元
【答案】
【分析】设这件夹克衫的成本为元,然后根据获利28元列出等式即可求出答案.
【解答】解:设这件夹克衫的成本为元,
,
解得:,
故选:.
8.某品牌奶茶进行促销活动,优惠措施是“第二杯半价”.现购买两杯该品牌奶茶,这两杯奶茶共打了
A.7折 B.7.5折 C.8折 D.8.5折
【答案】
【分析】设第一杯奶茶为元,则第二杯奶茶元,根据两杯奶茶的现价除以两杯奶茶的原价等于折扣率,列出代数式,计算即可得到结果.
【解答】解:设第一杯奶茶为元,则第二杯奶茶元,
由题意得:,
这两杯奶茶共打了7.5折.
故选:.
9.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送20件,还剩12件;若每个快递员派送24件,还差12件,设该分派站有名快递员,则可列方程为
A. B.
C. D.
【答案】
【分析】设该分派站有个快递员,根据“每个快递员派送20件,还剩12件;若每个快递员派送24件,还差12件”,即可得出关于的一元一次方程.
【解答】解:设该分派站有名快递员,则可列方程为:.
故选:.
10.我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问银子共有几两?设银子共有两,则可列方程为
A. B. C. D.
【答案】
【分析】根据“每人7两,还剩4两;每人9两,还差8两”,结合分银子的人数不变,即可得出关于的一元一次方程,此题得解.
【解答】解:银子共有两,每人7两,还剩4两,
分银子的人共人;
银子共有两,每人9两,还差8两,
分银子的人共人.
又分银子的人数不变,
可列方程组.
故选:.
二.填空题(共6小题)
11.现在是6点,至少经过 分钟,分针与时针互相垂直.
【答案】.
【分析】设再经过分钟,分针与时针互相垂直,根据角度差列出方程,解之即可.
【解答】解:6点整时,分钟与时针的夹角为,
设再经过分钟,分针与时针互相垂直,
则分针转了,时针转了,
由已知得:,
解得:,
故答案为:.
12.用150张白铁皮做罐头盒,每张白铁皮可制盒身15个或盒底41个,一个盒身与两个盒底配成一套罐头盒.设把张白铁皮制盒身,则可列方程为 .
【答案】.
【分析】设把张白铁皮制盒身,则张白铁皮制盒底,根据“一个盒身与两个盒底配成一套罐头盒”列出一元一次方程即可求解.
【解答】解:设把张白铁皮制盒身,则张白铁皮制盒底,根据题意得,
,
故答案为:.
13.如图,长方形被分割成六个正方形,其中最小正方形的面积等于1,则长方形的面积为 143 .
【答案】143.
【分析】给图中各正方形标上序号,设正方形4的边长为,则正方形3的边长为,正方形2的边长为,正方形1的边长为或,由正方形1的边长不变,可得出关于的一元一次方程,解之可得出的值,再将其代入中,即可求出结论.
【解答】解:给图中各正方形标上序号,如图所示
设正方形4的边长为,则正方形3的边长为,正方形2的边长为,正方形1的边长为或,
根据题意得:,
解得:,
,
长方形的面积为143.
故答案为:143.
14.《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 2 ,放入一个大球水面升高 ;
(2)如果放入10个球且使水面恰好上升到,应放入大球 个.
【答案】(1)2;3;
(2)6.
【分析】(1)利用放入一个小球水面上升高度放入小球的个数,可求出放入一个小球水面升高;利用放入一个大球水面上升高度放入大球的个数,可求出放入一个大球水面升高;
(2)设应放入个大球,则放入小球,利用水面上升的高度放入大球的个数放入小球的个数,可得出关于的一元一次方程,解之即可得出结论.
【解答】解:(1)根据题意得:放入一个小球水面升高;
放入一个大球水面升高.
故答案为:2;3;
(2)设应放入个大球,则放入小球,
根据题意得:,
解得:,
应放入大球6个.
故答案为:6.
15.如图的“”形图形的面积为,如果,那么 17 .
【答案】17.
【分析】将图形分成两个长方形,根据图形的面积建立方程,解方程即可得到答案.
【解答】解:如图所示,添加辅助线将图形分成两个长方形,
根据题意可得,
,
,
,
,
故答案为:17.
16.“好习惯受益终身”,每天早晨6时到7时之间都是七(1)班雯雯同学的“经典诵读”时间,从6时起,至少经过 分钟,时针与分针所形成的钝角等于.
【答案】.
【分析】先求出经过一分钟时针和分针分别转动的角度,设至少经过分钟,时针与分针所形成的钝角等于,再根据角的和差列出方程,求解即可.
【解答】解:经过一分针,分针转动的角度为:,时针转动的角度为:,
设至少经过分钟,时针与分针所形成的钝角等于,
由题意得:,
解得:,
设至少经过分钟,时针与分针所形成的钝角等于.
故答案为:.
三.解答题(共8小题)
17.某造纸厂为节约木材,大力扩大再生纸的生产,这家工厂去年10月生产再生纸2050吨,这比前年10月产量的2倍还多150吨,它前年10月生产再生纸多少吨?
【分析】设前年10月生产再生纸吨,则去年生产吨,从而可得方程,解出即可.
【解答】解:设前年10月生产再生纸吨,则去年生产吨,
由题意,得:,
解得:.
答:它前年10月生产再生纸950吨.
18.如图,小明用一张正方形纸片剪出两个宽都是的长条,如果其中一个长条的面积是另一个长条的1.2倍,求原来正方形纸片的边长.
【答案】.
【分析】设小长条的长为,则原来正方形的边长为,然后计算两个长条的面积,再利用面积关系列出方程求,即可求出原正方形的边长.
【解答】解:设小长条的长为,则原来正方形的边长为,
小长条的面积为:,大长条的面积为:,
其中一个长条的面积是另一个长条的1.2倍,
,
解得:,
原来正方形纸片的边长为.
故原来正方形纸片的边长为.
19.为了庆祝商都正式营业,商都推出了两种购物方案,方案一:非会员购物所有商品价格可获得九五折优惠:方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额.
(2)若某人计划在商都买价格为5000元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案下支出金额相同?
【答案】(1)方案一支出金额:元,方案二支出金额:元;
(2)买价格为5000元的电视机,选择方案一更省钱;
(3)商品价格为6000元时,两种方案下支出金额相同.
【分析】(1)由已知直接可得答案;
(2)分别计算出商品价格为5000元时,两种方案支付的金额,再比较即可;
(3)根据金额相同列出方程,即可解得答案.
【解答】解:(1)方案一支出金额:元,
方案二支出金额:元;
(2)买价格为5000元的电视机,
方案一支出金额:(元,
方案二支出金额:(元;
,
选择方案一更省钱;
(3)根据题意得:
,
解得,
答:商品价格为6000元时,两种方案下支出金额相同.
20.(列方程解应用题)小明一年前存入银行一笔钱,年利率为,到期共获得本息和为10225元,求小明一年前存入银行的本金是多少元?
【答案】10000元.
【分析】设小明一年前存入银行的本金是元,根据到期共获得本息和为10225元,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设小明一年前存入银行的本金是元,
依题意得:,
解得:.
答:小明一年前存入银行的本金是10000元.
21.某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为,每个大书包的盈利率为,试求两种书包的进价.
【分析】设每个小书包的进价为元,则每个大书包的进价为元,根据利润进价盈利率结合两种书包的售后利润额相同,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设每个小书包的进价为元,则每个大书包的进价为元,
依题意,得:,
解得:,
.
答:每个小书包的进价为20元,每个大书包的进价为30元.
22.在学习《水箱变高了》一课时,张老师将一个半径,高的圆柱形橡皮泥模型,重新揉成一个半径为的圆柱形,此时圆柱形的高为多少呢?
(1)请画出变形前后模型的示意图,并在示意图上标注对应的已知数据;
(2)通过列方程求变形后模型的高.
【答案】(1)画示意图见解答过程;
(2)变形后模型的高为.
【分析】(1)根据题意画出图形即可.
(2)设变形后模型的高为,根据变形前后模型的体积不变列方程即可解得答案.
【解答】解:(1)如图:
(2)设变形后模型的高为,
根据题意得:,
解得,
答:变形后模型的高为.
23.某市为保障供水及道路安全,自来水有限公司排查地下管线密集区,决定改造一段已使用多年面临老化的自来水管,这项翻新工程如果由甲工程队单独改造需要12天,由乙工程队单独改造需要24天.现要求甲、乙两个工程队一起合作完成这项翻新工程,但由于工作调动的原因,该项工程完工时,乙工程队中途共离开了3天.问这项工程一共用了多少天?
【答案】9天.
【分析】设这项工程一共用了天,则甲工程队改造了天,乙工程队改造了天,根据甲工程队完成的改造任务量乙工程队完成的改造任务量整个改造任务量,即可得出关于的一元一次方程,解之即可求出这项工程所用时间.
【解答】解:设这项工程一共用了天,则甲工程队改造了天,乙工程队改造了天,
依题意得:,
解得:.
答:这项工程一共用了9天.
24.七年级(1)班在召开期末总结表彰会前,班主任安排班长去商店买奖品,下面是班长与售货员的对话:
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
【分析】设笔记本的单价为元,则钢笔的单价为元,根据总价单价数量,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设笔记本的单价为元,则钢笔的单价为元,
依题意,得:,
解得:,
.
答:笔记本的单价为3元,钢笔的单价为5元.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
