2023-2024学年数学人教版八年级上册12.2 全等三角形的判定—用SAS证全等 同步检测(含解析)
文档属性
| 名称 | 2023-2024学年数学人教版八年级上册12.2 全等三角形的判定—用SAS证全等 同步检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 692.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 00:00:00 | ||
图片预览


文档简介
12.2 全等三角形的判定--用SAS证全等
一、单选题
1.如图,在3×3的方格图中,每个小方格的边长都为1,则的度数为( )
A.89° B.90° C.91° D.92°
2.如图,已知,若用“”证明,还需加上条件( )
A. B. C. D.
3.如图,是的中线,E,F分别是和延长线上的点,且,连接,下列说法:
①;
②和面积相等;
③;
④;
⑤.
其中正确的有( )
A.1个 B.5个 C.3个 D.4个
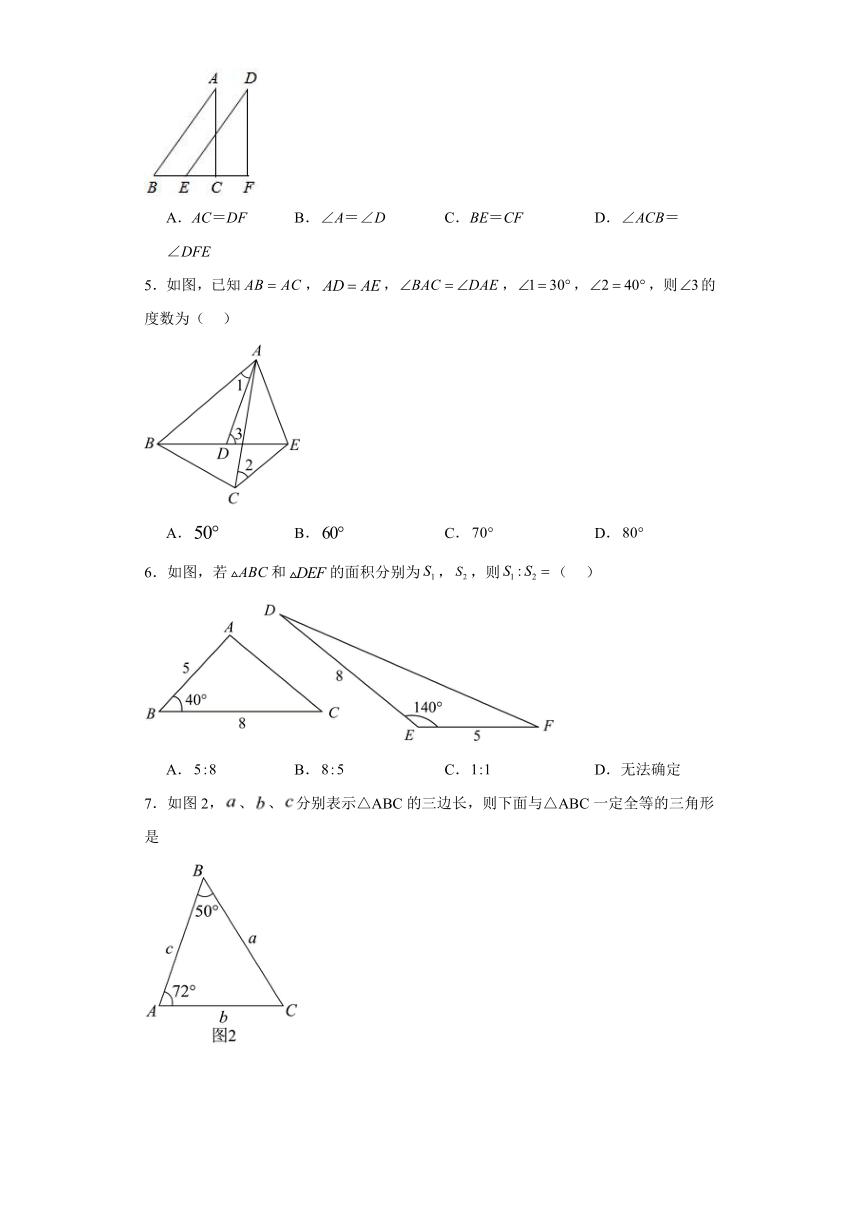
4.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
5.如图,已知,,,,,则的度数为( )
A. B. C. D.
6.如图,若和的面积分别为,,则( )
A. B. C. D.无法确定
7.如图2,、、分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是
B.
C.D.
8.如图,点E在AB上,点F在AC上,且AE=AF,AB=AC,BF=5,DE=1,则DC的长为( )
A.1 B.2 C.3 D.4
二、填空题
9.如图,已知,若以“”为依据证明,还需要添加的条件是 .
10.数学实践活动课中,老师布置了“测量小口圆柱形瓶底部内径”的探究任务,某学习小组设计了如下方案:如图,用螺丝钉将两根小棒的中点O固定,现测得C,D之间的距离为,那么小口圆柱形瓶底部的内径 .
11.如图,是外一点,是上一点,,,,,则的度数为 .
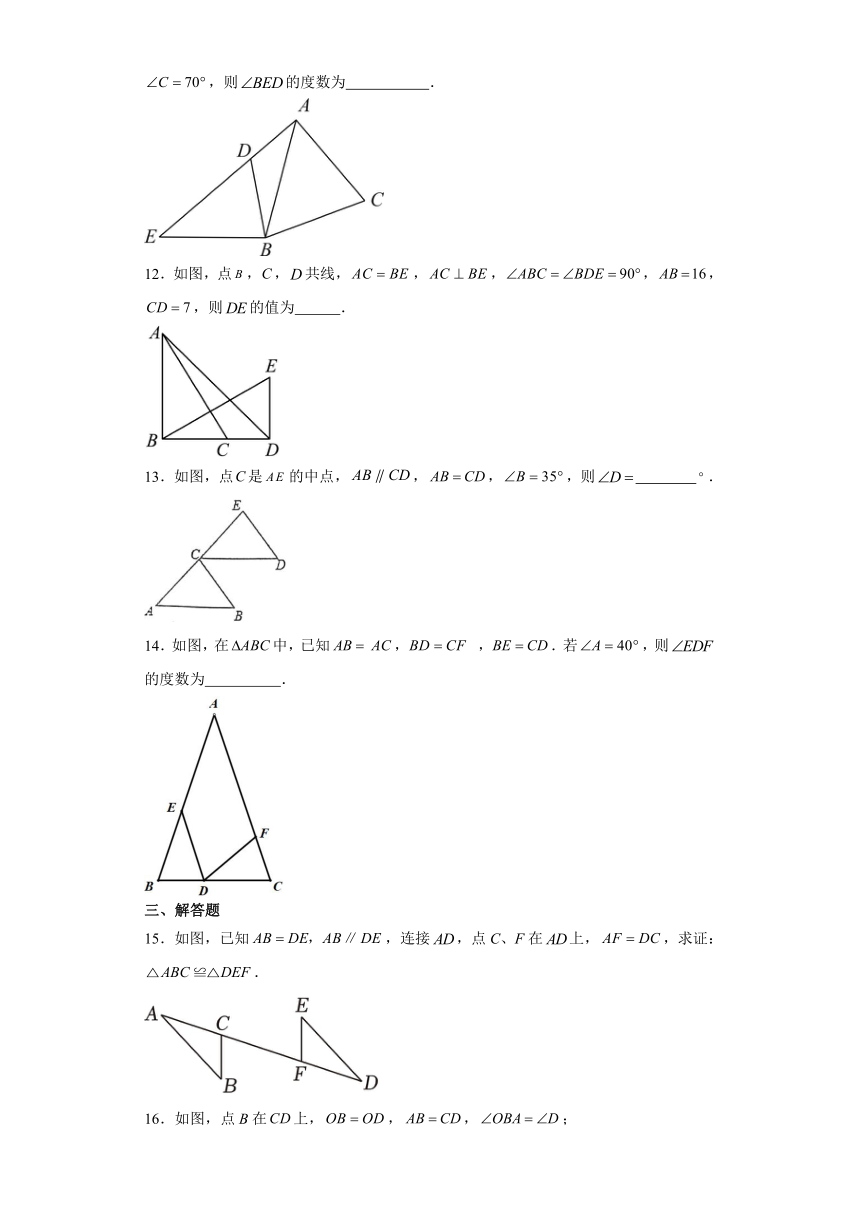
12.如图,点,,共线,,,,,,则的值为 .
13.如图,点是的中点,,,,则 .
14.如图,在中,已知, ,.若,则的度数为 .
三、解答题
15.如图,已知,连接,点C、F在上,,求证:.
16.如图,点B在上,,,;
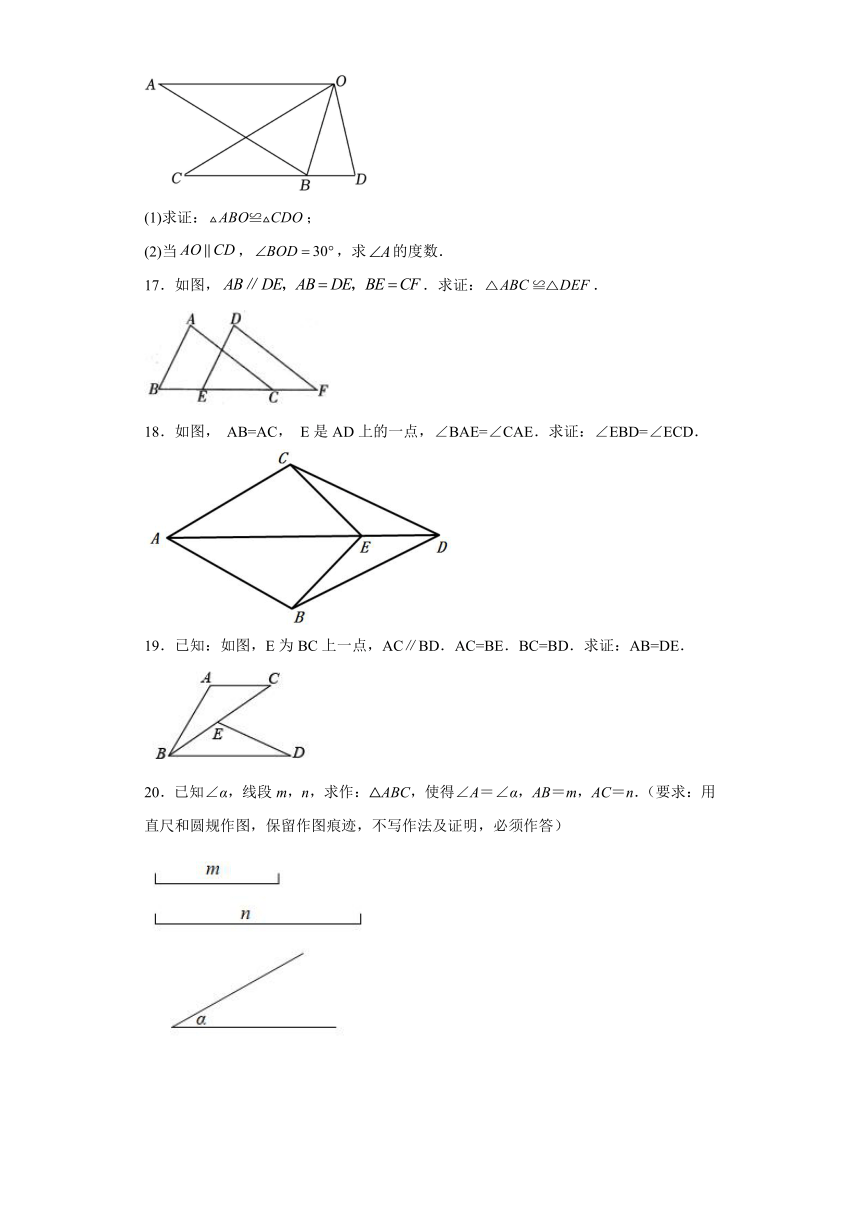
(1)求证:;
(2)当,,求的度数.
17.如图,.求证:.
18.如图, AB=AC, E是AD上的一点,∠BAE=∠CAE.求证:∠EBD=∠ECD.
19.已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
20.已知∠α,线段m,n,求作:△ABC,使得∠A=∠α,AB=m,AC=n.(要求:用直尺和圆规作图,保留作图痕迹,不写作法及证明,必须作答)
参考答案:
1.B
如图,
如图,在与中,
∴,
∴.
∵°,
∴
∴.
2.C
解:补充条件,
在与中
∴,
3.B
解:∵是的中线,
∴,
在和中,
,
∴,故④正确
∴,故①正确,
∵,
∴,故⑤正确,
∴,故③正确,
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的有5个,
4.C
解:补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF,
若要利用SAS判定,B、D选项不符合要求,
若A:AC=DF,构成的是SSA,不能证明三角形全等,A选项不符合要求,
C选项:BE=CF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
5.C
解:,
,即,
在和中,,
,
,
,
,
6.C
解:延长到使,连接,
,
,
,
在和中,
,
,
,
,
即:,
7.B
解:A、与三角形ABC有两边相等,而夹角不一定相等,二者不一定全等,不符合题意;
B、选项B与三角形ABC有两边及其夹边相等,二者全等,符合题意;
C、与三角形ABC有两边相等,但角不是夹角,二者不全等,不符合题意;
D、与三角形ABC有两角相等,但边不对应相等,二者不全等,不符合题意.
故答案选B.
8.D
解:在△BAF和△CAE中,
,
∴BAF≌△CAE(SAS),
∴BF=CE,
∵BF=5,DE=1,
∴CD=CE﹣DE=BF﹣DE=5﹣1=4,
9.
解:,,
添加条件,
故答案为:.
10.75
解:在和中,
,
∴,
∴,
故答案为:75.
11./35度
连接,
,,
是的垂直平分线,
,
在和中
,
,
故答案为:.
12.9
解:∵,,
∴,
∴,
在和中,
∵,
∴,
∴,
∴,
故答案为:9.
13.35
解:∵,
∴,
又∵,,
∴,
∴,
∵,
∴,
故答案为:35.
14.70°
∵AB=AC,∴∠B=∠C
∵BD=CF,BE=CD
∴△BED≌△CDE,∴∠EDC=∠BED
∵∠A=40°
∴∠B=∠C=70°
∴在△BED中,∠BED+∠BDE=110°
∴∠EDB+∠FDC=110°
∴∠EDF=70°
15.见解析
∵,
∴
∵,
∴,
即,
在与中,
,
∴.
16.(1)见解析
(2)的度数为
(1)证明:在中,
,
∴;
(2)解:∵,
∴,
∴,
∴,
∵,
∴,
∴.
17.见解析
证明:∵,
∴
∵,
∴,
在和中,
.
∴.
18.见解析
证明:在△ABD和△ACD中
∴△ABD≌△ACD,
∴∠ADB=∠ADC,BD=CD,
在△BDE和△CDE中
∴△BDE≌△CDE,
∴∠EBD=∠ECD.
19.详见解析
证明:∵AC∥BD,
∴∠ACB=∠DBC,
∵AC=BE,BC=BD,
∴△ABC≌△EDB,
∴AB=DE.
20.见解析
如图:
作图步骤:
①作射线,在射线上截取,
②以角的顶点为圆心,任意长度为半径作弧,交角的两边于,然后以点为圆心,同样长度为半径作弧,交于点,
③以为圆心,的长度为半径作弧交已知弧于点,
④作射线,在射线上截取,
⑤连接
则即为所求作的三角形.
一、单选题
1.如图,在3×3的方格图中,每个小方格的边长都为1,则的度数为( )
A.89° B.90° C.91° D.92°
2.如图,已知,若用“”证明,还需加上条件( )
A. B. C. D.
3.如图,是的中线,E,F分别是和延长线上的点,且,连接,下列说法:
①;
②和面积相等;
③;
④;
⑤.
其中正确的有( )
A.1个 B.5个 C.3个 D.4个
4.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
5.如图,已知,,,,,则的度数为( )
A. B. C. D.
6.如图,若和的面积分别为,,则( )
A. B. C. D.无法确定
7.如图2,、、分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是
B.
C.D.
8.如图,点E在AB上,点F在AC上,且AE=AF,AB=AC,BF=5,DE=1,则DC的长为( )
A.1 B.2 C.3 D.4
二、填空题
9.如图,已知,若以“”为依据证明,还需要添加的条件是 .
10.数学实践活动课中,老师布置了“测量小口圆柱形瓶底部内径”的探究任务,某学习小组设计了如下方案:如图,用螺丝钉将两根小棒的中点O固定,现测得C,D之间的距离为,那么小口圆柱形瓶底部的内径 .
11.如图,是外一点,是上一点,,,,,则的度数为 .
12.如图,点,,共线,,,,,,则的值为 .
13.如图,点是的中点,,,,则 .
14.如图,在中,已知, ,.若,则的度数为 .
三、解答题
15.如图,已知,连接,点C、F在上,,求证:.
16.如图,点B在上,,,;
(1)求证:;
(2)当,,求的度数.
17.如图,.求证:.
18.如图, AB=AC, E是AD上的一点,∠BAE=∠CAE.求证:∠EBD=∠ECD.
19.已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
20.已知∠α,线段m,n,求作:△ABC,使得∠A=∠α,AB=m,AC=n.(要求:用直尺和圆规作图,保留作图痕迹,不写作法及证明,必须作答)
参考答案:
1.B
如图,
如图,在与中,
∴,
∴.
∵°,
∴
∴.
2.C
解:补充条件,
在与中
∴,
3.B
解:∵是的中线,
∴,
在和中,
,
∴,故④正确
∴,故①正确,
∵,
∴,故⑤正确,
∴,故③正确,
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的有5个,
4.C
解:补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF,
若要利用SAS判定,B、D选项不符合要求,
若A:AC=DF,构成的是SSA,不能证明三角形全等,A选项不符合要求,
C选项:BE=CF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
5.C
解:,
,即,
在和中,,
,
,
,
,
6.C
解:延长到使,连接,
,
,
,
在和中,
,
,
,
,
即:,
7.B
解:A、与三角形ABC有两边相等,而夹角不一定相等,二者不一定全等,不符合题意;
B、选项B与三角形ABC有两边及其夹边相等,二者全等,符合题意;
C、与三角形ABC有两边相等,但角不是夹角,二者不全等,不符合题意;
D、与三角形ABC有两角相等,但边不对应相等,二者不全等,不符合题意.
故答案选B.
8.D
解:在△BAF和△CAE中,
,
∴BAF≌△CAE(SAS),
∴BF=CE,
∵BF=5,DE=1,
∴CD=CE﹣DE=BF﹣DE=5﹣1=4,
9.
解:,,
添加条件,
故答案为:.
10.75
解:在和中,
,
∴,
∴,
故答案为:75.
11./35度
连接,
,,
是的垂直平分线,
,
在和中
,
,
故答案为:.
12.9
解:∵,,
∴,
∴,
在和中,
∵,
∴,
∴,
∴,
故答案为:9.
13.35
解:∵,
∴,
又∵,,
∴,
∴,
∵,
∴,
故答案为:35.
14.70°
∵AB=AC,∴∠B=∠C
∵BD=CF,BE=CD
∴△BED≌△CDE,∴∠EDC=∠BED
∵∠A=40°
∴∠B=∠C=70°
∴在△BED中,∠BED+∠BDE=110°
∴∠EDB+∠FDC=110°
∴∠EDF=70°
15.见解析
∵,
∴
∵,
∴,
即,
在与中,
,
∴.
16.(1)见解析
(2)的度数为
(1)证明:在中,
,
∴;
(2)解:∵,
∴,
∴,
∴,
∵,
∴,
∴.
17.见解析
证明:∵,
∴
∵,
∴,
在和中,
.
∴.
18.见解析
证明:在△ABD和△ACD中
∴△ABD≌△ACD,
∴∠ADB=∠ADC,BD=CD,
在△BDE和△CDE中
∴△BDE≌△CDE,
∴∠EBD=∠ECD.
19.详见解析
证明:∵AC∥BD,
∴∠ACB=∠DBC,
∵AC=BE,BC=BD,
∴△ABC≌△EDB,
∴AB=DE.
20.见解析
如图:
作图步骤:
①作射线,在射线上截取,
②以角的顶点为圆心,任意长度为半径作弧,交角的两边于,然后以点为圆心,同样长度为半径作弧,交于点,
③以为圆心,的长度为半径作弧交已知弧于点,
④作射线,在射线上截取,
⑤连接
则即为所求作的三角形.
