2023-2024学年人教版数学九年级上册24.4弧长及扇形的面积 同步练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级上册24.4弧长及扇形的面积 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 176.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 00:00:00 | ||
图片预览



文档简介
24.4弧长及扇形的面积 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.已知扇形半径为3,弧长为π,则它所对的圆心角的度数为( )
A.120° B.60° C.40° D.20°
2.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A.2, B.2 ,π C. , D.2 ,
3.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是( )
A. B. C. D.
4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2 B. C. D.
5.如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
A.π﹣2 B.2π﹣2 C.4π﹣4 D.4π﹣8
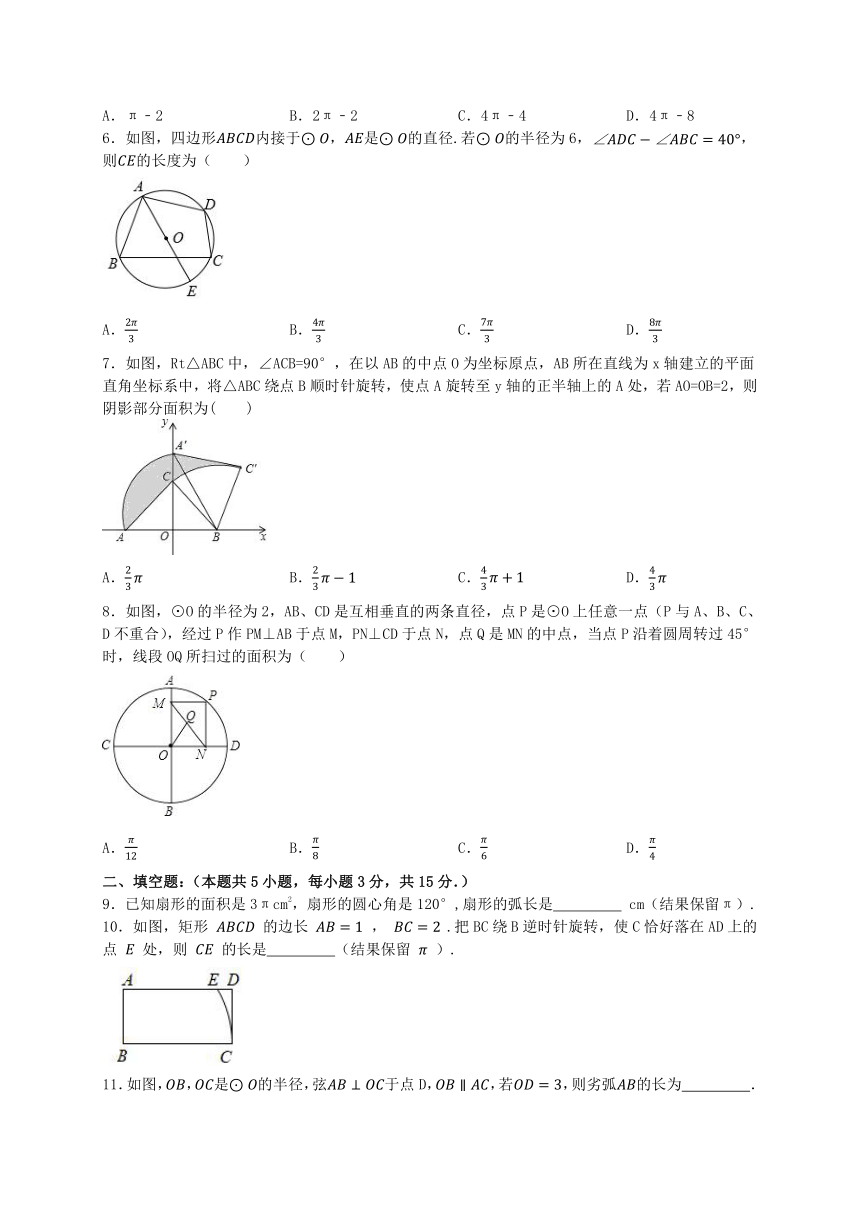
6.如图,四边形内接于,是的直径.若的半径为6,,则的长度为( )
A. B. C. D.
7.如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A. B. C. D.
8.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过的面积为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知扇形的面积是3πcm2,扇形的圆心角是120°,扇形的弧长是 cm(结果保留π).
10.如图,矩形 的边长 , .把BC绕B逆时针旋转,使C恰好落在AD上的点 处,则 的长是 (结果保留 ).
11.如图,,是的半径,弦于点D,,若,则劣弧的长为 .
12.如图,点O为 斜边 上的一点,以 为半径的 与边 相切于点D,与边 相交于点E,连接 ,若 平分 ,且 , ,则图中阴影部分的面积为 .
13. 是⊙ 内接三角形, 是⊙ 的直径, , ,弦 所对的弧长为 .
三、解答题:(本题共5题,共45分)
14.如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,求点B转过的路径长.
15.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,求图中阴影部分的面积.
16.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
17.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一动点且不与点A,C重合,AG,DC的延长线交于点F,连结BC.CD=,BE=2.
(1)求半径长。
(2)求扇形DOC的面积;
18.如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是 的中点,⊙O的半径为1,求图中阴影部分的面积
参考答案:
1.B 2.D 3.A 4.B 5.A 6.B 7.D 8.B
9.2π
10.
11.4π
12.
13. 或
14.∵∠B=30°,AC=2
∴BA=4∠A=60°,
∴CB=6,
∵AC=A′C,
∴∠AA′C是等边三角形,
∴∠ACA′=60°,
∴∠BCB′=60°,
∴弧长l=
故答案为:2π.
15.解:如图,连接BD,
∵四边形ABCD是菱形,∠A=60°,
∴△ABD和△BCD是等边三角形,
∴BD=BC,∠ADB=∠DBC=∠C=60°,
∵扇形圆心角∠EBF=60°,
∴∠DBE+∠DBF=∠CBF+∠DBH=60°,
∴∠DBE=∠CBF,
在△BDG和△BCH中,
,
∴△BDG≌△BCH(ASA),
∴S△BDG=S△BCH,
∵AB=2,扇形BEF的半径为2,
∴S阴影=﹣×2×(2×)=π﹣.
16.(1)证明:连接OD,
∵BC是⊙O的切线,
∴∠ABC=90°,
∵CD=CB,
∴∠CBD=∠CDB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODC=∠ABC=90°,
即OD⊥CD,
∵点D在⊙O上,
∴CD为⊙O的切线
(2)解:在Rt△OBF中,
∵∠ABD=30°,OF=1,
∴∠BOF=60°,OB=2,BF= ,
∵OF⊥BD,
∴BD=2BF=2 ,∠BOD=2∠BOF=120°,
∴S阴影=S扇形OBD﹣S△BOD= ﹣ ×2 ×1= π﹣ .
17.(1)解:如图所示,连接OD,
设OD=OB=r,
∵AB是直径,AB⊥CD,CD=,
∴DE=EC= ,
在Rt△ODE中,由勾股定理得:OD2=OE2+DE2,
∴r2=(r-2)2+12,
解得r=4,
∴⊙O的半径为4.
(2)解:如图所示,连接OC,
∵在Rt△ODE中,DO=4,OE=2,
∴∠ODE=30°,
∵OD=OC,
∴∠OCD=30°,
∴∠DOC=120°,
∴扇形DOC的面积==.
18.(1)解:CD与圆O相切.理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切
(2)解:连接EB,交OC于F,
∵E为 的中点,
∴ ,
∴AE=EC,
∴∠EAC=∠ECA,
又∵∠EAC=∠OAC,
∴∠ECA=∠OAC,
∴CE∥OA,
又∵OC∥AD,
∴四边形AOCE是平行四边形,
∴CE=OA,AE=OC,
又∵OA=OC=1,
∴四边形AOCE是菱形,
∵AB为直径,得到∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF= AE= ,即CF=DE= ,
在Rt△OBF中,根据勾股定理得:EF=FB=DC= ,
则S阴影=S△DEC= × × = .
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.已知扇形半径为3,弧长为π,则它所对的圆心角的度数为( )
A.120° B.60° C.40° D.20°
2.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A.2, B.2 ,π C. , D.2 ,
3.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC= ,则图中阴影部分的面积是( )
A. B. C. D.
4.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2 B. C. D.
5.如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
A.π﹣2 B.2π﹣2 C.4π﹣4 D.4π﹣8
6.如图,四边形内接于,是的直径.若的半径为6,,则的长度为( )
A. B. C. D.
7.如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A. B. C. D.
8.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过的面积为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知扇形的面积是3πcm2,扇形的圆心角是120°,扇形的弧长是 cm(结果保留π).
10.如图,矩形 的边长 , .把BC绕B逆时针旋转,使C恰好落在AD上的点 处,则 的长是 (结果保留 ).
11.如图,,是的半径,弦于点D,,若,则劣弧的长为 .
12.如图,点O为 斜边 上的一点,以 为半径的 与边 相切于点D,与边 相交于点E,连接 ,若 平分 ,且 , ,则图中阴影部分的面积为 .
13. 是⊙ 内接三角形, 是⊙ 的直径, , ,弦 所对的弧长为 .
三、解答题:(本题共5题,共45分)
14.如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,求点B转过的路径长.
15.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,求图中阴影部分的面积.
16.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
17.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一动点且不与点A,C重合,AG,DC的延长线交于点F,连结BC.CD=,BE=2.
(1)求半径长。
(2)求扇形DOC的面积;
18.如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是 的中点,⊙O的半径为1,求图中阴影部分的面积
参考答案:
1.B 2.D 3.A 4.B 5.A 6.B 7.D 8.B
9.2π
10.
11.4π
12.
13. 或
14.∵∠B=30°,AC=2
∴BA=4∠A=60°,
∴CB=6,
∵AC=A′C,
∴∠AA′C是等边三角形,
∴∠ACA′=60°,
∴∠BCB′=60°,
∴弧长l=
故答案为:2π.
15.解:如图,连接BD,
∵四边形ABCD是菱形,∠A=60°,
∴△ABD和△BCD是等边三角形,
∴BD=BC,∠ADB=∠DBC=∠C=60°,
∵扇形圆心角∠EBF=60°,
∴∠DBE+∠DBF=∠CBF+∠DBH=60°,
∴∠DBE=∠CBF,
在△BDG和△BCH中,
,
∴△BDG≌△BCH(ASA),
∴S△BDG=S△BCH,
∵AB=2,扇形BEF的半径为2,
∴S阴影=﹣×2×(2×)=π﹣.
16.(1)证明:连接OD,
∵BC是⊙O的切线,
∴∠ABC=90°,
∵CD=CB,
∴∠CBD=∠CDB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODC=∠ABC=90°,
即OD⊥CD,
∵点D在⊙O上,
∴CD为⊙O的切线
(2)解:在Rt△OBF中,
∵∠ABD=30°,OF=1,
∴∠BOF=60°,OB=2,BF= ,
∵OF⊥BD,
∴BD=2BF=2 ,∠BOD=2∠BOF=120°,
∴S阴影=S扇形OBD﹣S△BOD= ﹣ ×2 ×1= π﹣ .
17.(1)解:如图所示,连接OD,
设OD=OB=r,
∵AB是直径,AB⊥CD,CD=,
∴DE=EC= ,
在Rt△ODE中,由勾股定理得:OD2=OE2+DE2,
∴r2=(r-2)2+12,
解得r=4,
∴⊙O的半径为4.
(2)解:如图所示,连接OC,
∵在Rt△ODE中,DO=4,OE=2,
∴∠ODE=30°,
∵OD=OC,
∴∠OCD=30°,
∴∠DOC=120°,
∴扇形DOC的面积==.
18.(1)解:CD与圆O相切.理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切
(2)解:连接EB,交OC于F,
∵E为 的中点,
∴ ,
∴AE=EC,
∴∠EAC=∠ECA,
又∵∠EAC=∠OAC,
∴∠ECA=∠OAC,
∴CE∥OA,
又∵OC∥AD,
∴四边形AOCE是平行四边形,
∴CE=OA,AE=OC,
又∵OA=OC=1,
∴四边形AOCE是菱形,
∵AB为直径,得到∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF= AE= ,即CF=DE= ,
在Rt△OBF中,根据勾股定理得:EF=FB=DC= ,
则S阴影=S△DEC= × × = .
同课章节目录
