第十一章 三角形 单元复习课件(29张PPT)
文档属性
| 名称 | 第十一章 三角形 单元复习课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 41.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 09:29:38 | ||
图片预览







文档简介
(共29张PPT)
第11章
三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
单元复盘提升
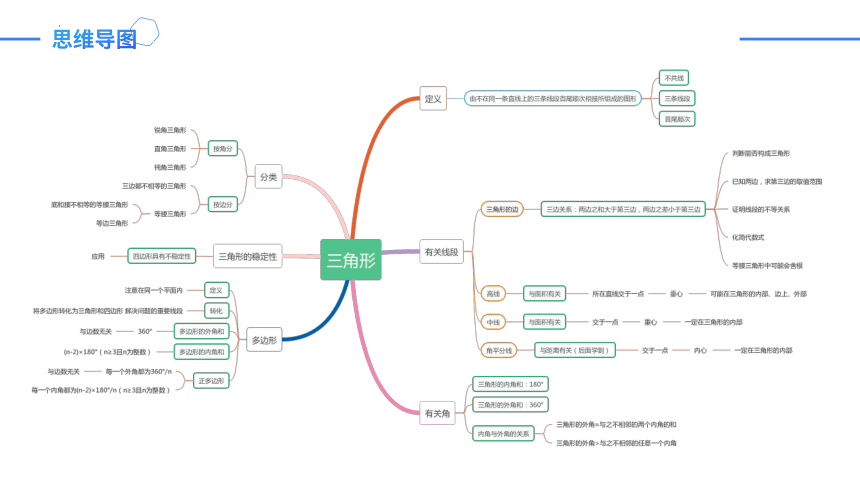
思维导图
知识串讲
底边和腰不相等的等腰三角形
2. 三角形的三边关系:
1. 三角形的分类
三角形的两边之和大于第三边,两边之差小于第三边.
按边分
按角分
三边都不相等的三角形
等腰三角形
等边三角形
直角三角形
锐角三角形
钝角三角形
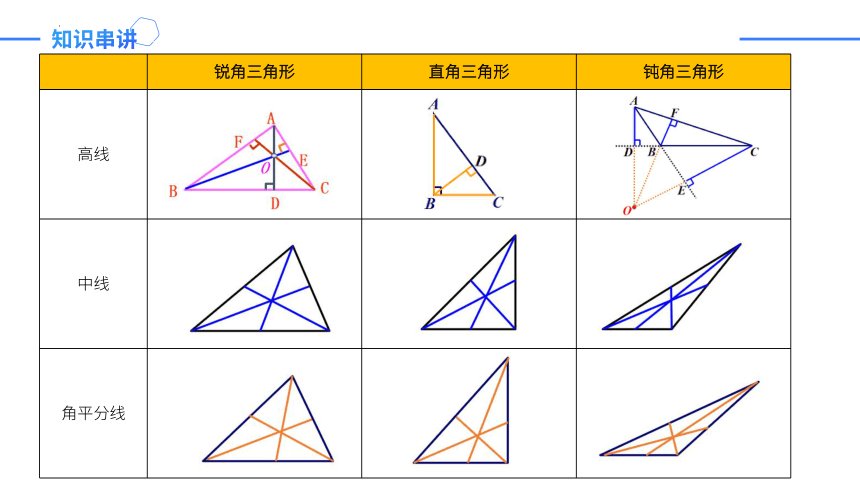
知识串讲
3. 三角形的高、中线与角平分线
高:过顶点向其对边所在直线引垂线,
所得垂线段为高.三条高或其延长线相交于一点,
如图①.
中线:连接顶点与其对边中点所得线段为中线.
三条中线相交于一点(重心),
如图②.
角平分线:内角的平分线与其对边相交所得线段为角平分线.三条角平分线相交于一点,
如图③.
图①
图②
图③
知识串讲
锐角三角形 直角三角形 钝角三角形
高线
中线
角平分线
知识串讲
4. 三角形的内角和定理与外角的性质
(1) 三角形的内角和等于 180°;
(2) 三角形的一个外角等于与它不相邻的两个内角的和;
(3) 三角形的一个外角大于和它不相邻的任何一个内角.
5. 多边形及其内角和
n 边形内角和等于 (n - 2)×180°(n≥3,且 n 为整数).
n 边形的外角和等于 360°.
正 n 边形的每个内角的度数是
正 n 边形的每个外角的度数是
考点梳理
考点一:三角形三边关系
把一条长为18米的细绳围成一个三角形, 其中两段长分别为x米和4米.
(1)求x的取值范围;
(2)若围成的三角形是等腰三角形时,求x的值.
例1
解:(1)∵该三角形的周长是18米,其中两段长分别为x米和4米,
∴第三边的长度是18-4-x=14-x(米).
∴14-x-4<x<14-x+4,解得5<x<9.
∴x的取值范围是:5<x<9.
考点梳理
考点一:三角形三边关系
把一条长为18米的细绳围成一个三角形, 其中两段长分别为x米和4米.
(1)求x的取值范围;
(2)若围成的三角形是等腰三角形时,求x的值.
例1
(2)①当边长为x米的边为等腰三角形的底时,
x+4+4=18,解得,x=10,
∵10>9,∴x=10,不合题意,舍去.
②当边长为4米的边为等腰三角形的底时,
2x+4=18,解得,x=7. 综上所述,x的值是7.
等腰三角反复讲
分类讨论不能忘
刻意练习
练1
一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
练2
如图,D是△ABC 的边AC上一点,AD=BD,试判断AC 与BC 的大小.
解:在△BDC 中,
有 BD+DC >BC
又因为 AD = BD,
则BD+DC = AD+DC = AC,
所以 AC >BC.
考点梳理
考点二:三角形中的线段
例2
作△ABC的边AB上的高,下列作法中,正确的是( )
D
考点梳理
考点二:三角形中的线段
例3
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
考点梳理
考点二:三角形中的线段
例4
在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
解:如图,∵DB为△ABC的中线,
∴AD=CD,
设AD=CD=x,则AB=2x,
当x+2x=12,解得x=4.
BC+x=15,得BC=11.
此时△ABC的三边长为AB=AC=8,BC=11;
当x+2x=15,BC+x=12,解得x=5,BC=7,
此时△ABC的三边长为AB=AC=10,BC=7.
刻意练习
练3
解:∵ 点 E 是 AD 的中点,
∴ S△DBE = S△ABD,S△DCE = S△ADC.
∴ S△DBE + S△DCE = S△ABC = ×24 = 12,即 S△BCE = 12.
∵ 点 F 是 CE 的中点,∴ S△BEF = S△BCE = ×12 = 6.
如图,D 是△ABC 的边 BC 上任意一点,E、F 分别是线段 AD、CE 的中点,且△ABC 的面积为 24,求△BEF 的面积.
刻意练习
练4
如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
考点梳理
考点三:与三角形有关的角度计算
例5
【例2】如右图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=__________度;(2)求∠EDF的度数.
解:(1)由折叠得∠DAF=∠BAD=30°,
∴∠BAF=60°,∴∠AFC=∠B+∠BAF=110°;
(2)由折叠得∠E=∠B=50°,又∠DFE=∠AFC=110°,
∴∠EDF=180°-∠E-∠DFE=20°.
考点梳理
考点三:与三角形有关的角度计算
例6
如图,在△ABC 中,D 是 BC 边上一点,∠1 =∠2,∠3 =∠4,∠BAC = 63°,求∠DAC 的度数.
解:设∠1 =∠2 = x,则∠4 =∠3 = 2x.
∵∠BAC = 63°,
∴∠2 +∠4 = 117°,即 x + 2x = 117°.
∴ x = 39°.
∴∠3 = ∠4 = 78°,
∠DAC = 180° - ∠3 - ∠4 = 24°.
外角内角齐上阵
方程思想来相等
刻意练习
练5
如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B恰好落在CD边上的点H处,且∠CHE=40°.
(1)求∠HFA的度数;
(2)求∠HEF的度数.
(1)由折叠得∠EHF=∠B=90°,
∴∠CHF=90°+40°=130°,∵DC∥AB,
∴∠HFA=∠CHF=130°.
(2)∵∠CEH=180°-∠C -∠CHE=50°,
∴∠HEB=180°-∠CEH=130°,
由折叠得∠HEF=∠BEF,∴∠HEF= ∠HEB=65°.
折叠必有对称美
寻找对应角和边
刻意练习
练6
如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
考点梳理
考点四:多边形的内角与外角相关计算
例7
一个正多边形的每个外角是45°.
(1)试求这个多边形的边数;(2)求这个多边形内角和的度数.
解:(1)方法一:设这个多边形的边数为n,得:45n=360,
解得:n=8.∴这个多边形的边数为8.
方法二:多边形每一个内角为:180°-45°=135°.
设这个多边形的边数为n,得:(n-2)×180=135×n,
解得:n=8.∴这个多边形的边数为8.
(2)这个多边形内角和的度数为
(n-2)×180°=(8-2)×180°=1080°.
考点梳理
考点四:多边形的内角与外角相关计算
例8
如下图所示,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
解:连接BE,∵∠D+∠C+∠DOC=180°,
∠OBE+∠OEB+∠BOE=180°
又∠DOC=∠BOE,∴∠OBE+∠OEB=∠C+∠D,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G
=∠A+∠ABC+∠OBE+∠OEB+∠DEF+∠F+∠G
=∠A+∠ABE+∠BEF+∠F+∠G
=(5-2)×180°=540°.
本章重点回顾
化繁为简三秋见
化归未知为已知
刻意练习
练7
解:(1)设多边形的边数为n,由题意得15n=360,
解得n=24,24×5=120(米).
(2)(n-2)·180°=(24-2)×180°=3 960°
如下图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,……这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
刻意练习
练8
已知一个多边形的内角和比它的外角和的 3 倍少180°,求这个多边形的边数.
解:设这个多边形的边数是 n,
依题意得 (n-2)×180° = 3×360°-180°,
解得 n = 7.
∴ 这个多边形的边数是 7.
模型总结
模型一:三角形的重心
模型总结
模型二:三角形的面积比与线段比
模型总结
模型三:八字型
模型总结
模型三:八字型
模型总结
模型四:双垂直模型
课程小结
第11章
三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
单元复盘提升
思维导图
知识串讲
底边和腰不相等的等腰三角形
2. 三角形的三边关系:
1. 三角形的分类
三角形的两边之和大于第三边,两边之差小于第三边.
按边分
按角分
三边都不相等的三角形
等腰三角形
等边三角形
直角三角形
锐角三角形
钝角三角形
知识串讲
3. 三角形的高、中线与角平分线
高:过顶点向其对边所在直线引垂线,
所得垂线段为高.三条高或其延长线相交于一点,
如图①.
中线:连接顶点与其对边中点所得线段为中线.
三条中线相交于一点(重心),
如图②.
角平分线:内角的平分线与其对边相交所得线段为角平分线.三条角平分线相交于一点,
如图③.
图①
图②
图③
知识串讲
锐角三角形 直角三角形 钝角三角形
高线
中线
角平分线
知识串讲
4. 三角形的内角和定理与外角的性质
(1) 三角形的内角和等于 180°;
(2) 三角形的一个外角等于与它不相邻的两个内角的和;
(3) 三角形的一个外角大于和它不相邻的任何一个内角.
5. 多边形及其内角和
n 边形内角和等于 (n - 2)×180°(n≥3,且 n 为整数).
n 边形的外角和等于 360°.
正 n 边形的每个内角的度数是
正 n 边形的每个外角的度数是
考点梳理
考点一:三角形三边关系
把一条长为18米的细绳围成一个三角形, 其中两段长分别为x米和4米.
(1)求x的取值范围;
(2)若围成的三角形是等腰三角形时,求x的值.
例1
解:(1)∵该三角形的周长是18米,其中两段长分别为x米和4米,
∴第三边的长度是18-4-x=14-x(米).
∴14-x-4<x<14-x+4,解得5<x<9.
∴x的取值范围是:5<x<9.
考点梳理
考点一:三角形三边关系
把一条长为18米的细绳围成一个三角形, 其中两段长分别为x米和4米.
(1)求x的取值范围;
(2)若围成的三角形是等腰三角形时,求x的值.
例1
(2)①当边长为x米的边为等腰三角形的底时,
x+4+4=18,解得,x=10,
∵10>9,∴x=10,不合题意,舍去.
②当边长为4米的边为等腰三角形的底时,
2x+4=18,解得,x=7. 综上所述,x的值是7.
等腰三角反复讲
分类讨论不能忘
刻意练习
练1
一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
练2
如图,D是△ABC 的边AC上一点,AD=BD,试判断AC 与BC 的大小.
解:在△BDC 中,
有 BD+DC >BC
又因为 AD = BD,
则BD+DC = AD+DC = AC,
所以 AC >BC.
考点梳理
考点二:三角形中的线段
例2
作△ABC的边AB上的高,下列作法中,正确的是( )
D
考点梳理
考点二:三角形中的线段
例3
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
考点梳理
考点二:三角形中的线段
例4
在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
解:如图,∵DB为△ABC的中线,
∴AD=CD,
设AD=CD=x,则AB=2x,
当x+2x=12,解得x=4.
BC+x=15,得BC=11.
此时△ABC的三边长为AB=AC=8,BC=11;
当x+2x=15,BC+x=12,解得x=5,BC=7,
此时△ABC的三边长为AB=AC=10,BC=7.
刻意练习
练3
解:∵ 点 E 是 AD 的中点,
∴ S△DBE = S△ABD,S△DCE = S△ADC.
∴ S△DBE + S△DCE = S△ABC = ×24 = 12,即 S△BCE = 12.
∵ 点 F 是 CE 的中点,∴ S△BEF = S△BCE = ×12 = 6.
如图,D 是△ABC 的边 BC 上任意一点,E、F 分别是线段 AD、CE 的中点,且△ABC 的面积为 24,求△BEF 的面积.
刻意练习
练4
如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
考点梳理
考点三:与三角形有关的角度计算
例5
【例2】如右图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=__________度;(2)求∠EDF的度数.
解:(1)由折叠得∠DAF=∠BAD=30°,
∴∠BAF=60°,∴∠AFC=∠B+∠BAF=110°;
(2)由折叠得∠E=∠B=50°,又∠DFE=∠AFC=110°,
∴∠EDF=180°-∠E-∠DFE=20°.
考点梳理
考点三:与三角形有关的角度计算
例6
如图,在△ABC 中,D 是 BC 边上一点,∠1 =∠2,∠3 =∠4,∠BAC = 63°,求∠DAC 的度数.
解:设∠1 =∠2 = x,则∠4 =∠3 = 2x.
∵∠BAC = 63°,
∴∠2 +∠4 = 117°,即 x + 2x = 117°.
∴ x = 39°.
∴∠3 = ∠4 = 78°,
∠DAC = 180° - ∠3 - ∠4 = 24°.
外角内角齐上阵
方程思想来相等
刻意练习
练5
如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B恰好落在CD边上的点H处,且∠CHE=40°.
(1)求∠HFA的度数;
(2)求∠HEF的度数.
(1)由折叠得∠EHF=∠B=90°,
∴∠CHF=90°+40°=130°,∵DC∥AB,
∴∠HFA=∠CHF=130°.
(2)∵∠CEH=180°-∠C -∠CHE=50°,
∴∠HEB=180°-∠CEH=130°,
由折叠得∠HEF=∠BEF,∴∠HEF= ∠HEB=65°.
折叠必有对称美
寻找对应角和边
刻意练习
练6
如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
考点梳理
考点四:多边形的内角与外角相关计算
例7
一个正多边形的每个外角是45°.
(1)试求这个多边形的边数;(2)求这个多边形内角和的度数.
解:(1)方法一:设这个多边形的边数为n,得:45n=360,
解得:n=8.∴这个多边形的边数为8.
方法二:多边形每一个内角为:180°-45°=135°.
设这个多边形的边数为n,得:(n-2)×180=135×n,
解得:n=8.∴这个多边形的边数为8.
(2)这个多边形内角和的度数为
(n-2)×180°=(8-2)×180°=1080°.
考点梳理
考点四:多边形的内角与外角相关计算
例8
如下图所示,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
解:连接BE,∵∠D+∠C+∠DOC=180°,
∠OBE+∠OEB+∠BOE=180°
又∠DOC=∠BOE,∴∠OBE+∠OEB=∠C+∠D,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G
=∠A+∠ABC+∠OBE+∠OEB+∠DEF+∠F+∠G
=∠A+∠ABE+∠BEF+∠F+∠G
=(5-2)×180°=540°.
本章重点回顾
化繁为简三秋见
化归未知为已知
刻意练习
练7
解:(1)设多边形的边数为n,由题意得15n=360,
解得n=24,24×5=120(米).
(2)(n-2)·180°=(24-2)×180°=3 960°
如下图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,……这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
刻意练习
练8
已知一个多边形的内角和比它的外角和的 3 倍少180°,求这个多边形的边数.
解:设这个多边形的边数是 n,
依题意得 (n-2)×180° = 3×360°-180°,
解得 n = 7.
∴ 这个多边形的边数是 7.
模型总结
模型一:三角形的重心
模型总结
模型二:三角形的面积比与线段比
模型总结
模型三:八字型
模型总结
模型三:八字型
模型总结
模型四:双垂直模型
课程小结
