5.1 平行四边形的性质 第3课时 两条平行线之间的距离(含答案)
文档属性
| 名称 | 5.1 平行四边形的性质 第3课时 两条平行线之间的距离(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 08:11:04 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
1 平行四边形的性质
第3课时 两条平行线之间的距离
刷基础
知识点 平行线间的距离
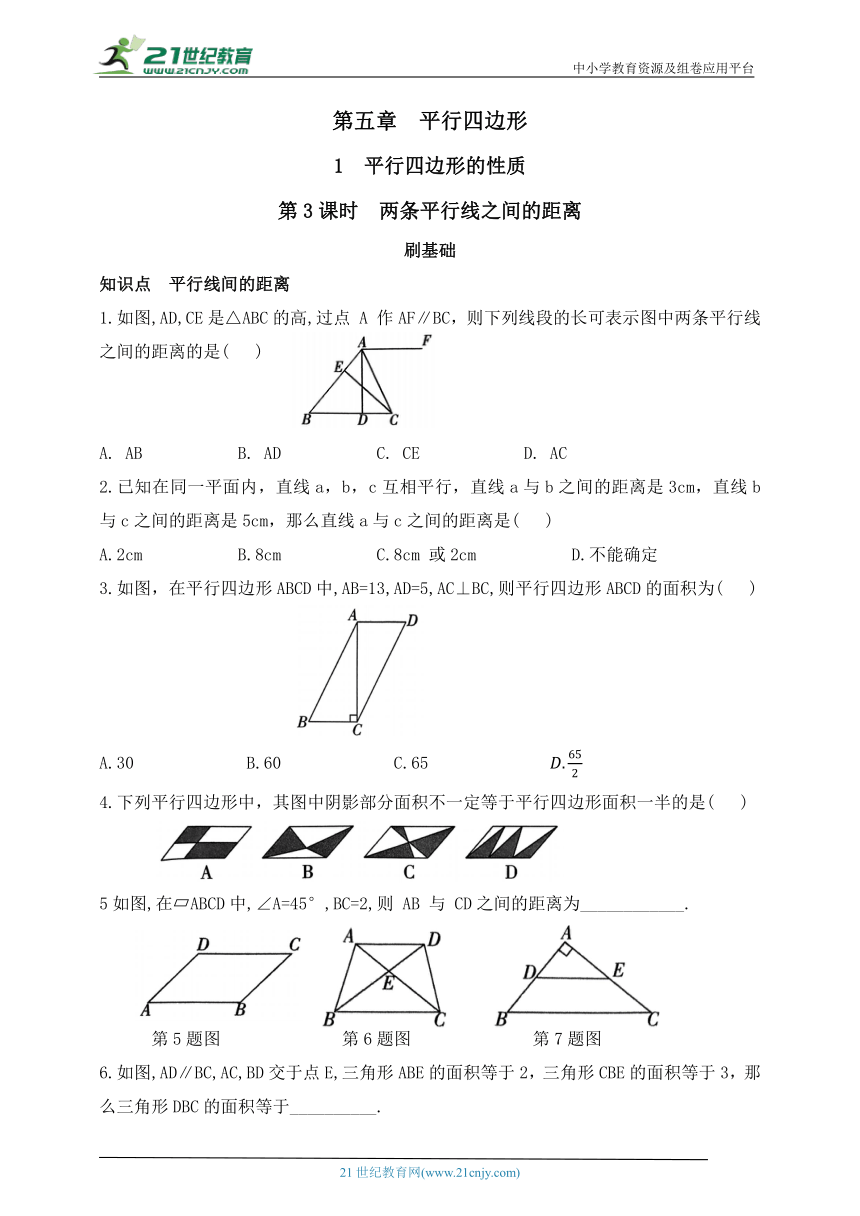
1.如图,AD,CE是△ABC的高,过点 A 作AF∥BC,则下列线段的长可表示图中两条平行线之间的距离的是( )
A. AB B. AD C. CE D. AC
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c之间的距离是( )
A.2cm B.8cm C.8cm 或2cm D.不能确定
3.如图,在平行四边形ABCD中,AB=13,AD=5,AC⊥BC,则平行四边形ABCD的面积为( )
A.30 B.60 C.65
4.下列平行四边形中,其图中阴影部分面积不一定等于平行四边形面积一半的是( )
5如图,在 ABCD中,∠A=45°,BC=2,则 AB 与 CD之间的距离为____________.
第5题图 第6题图 第7题图
6.如图,AD∥BC,AC,BD交于点E,三角形ABE的面积等于2,三角形CBE的面积等于3,那么三角形DBC的面积等于__________.
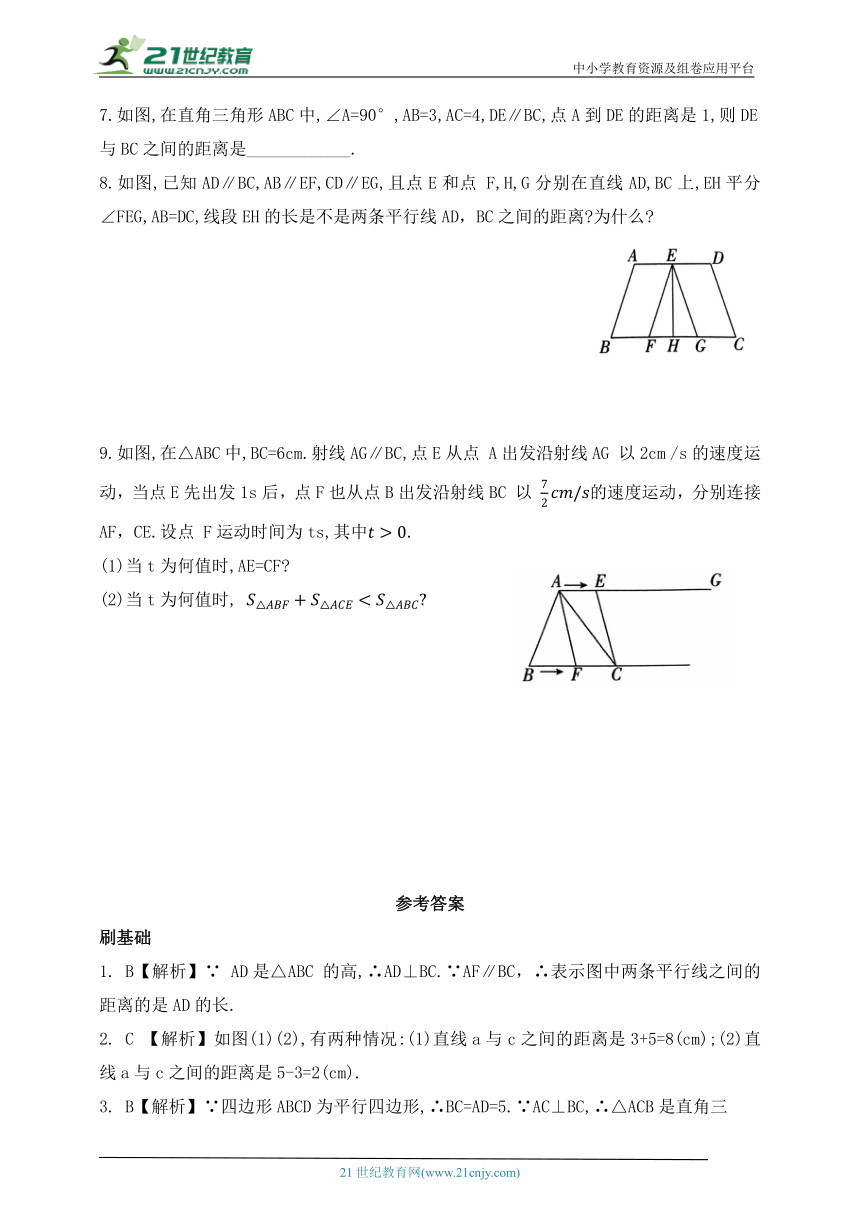
7.如图,在直角三角形ABC中,∠A=90°,AB=3,AC=4,DE∥BC,点A到DE的距离是1,则DE
与BC之间的距离是____________.
8.如图,已知AD∥BC,AB∥EF,CD∥EG,且点E和点 F,H,G分别在直线AD,BC上,EH平分 ∠FEG,AB=DC,线段EH的长是不是两条平行线AD,BC之间的距离 为什么
9.如图,在△ABC中,BC=6cm.射线AG∥BC,点E从点 A出发沿射线AG 以2cm /s的速度运动,当点E先出发1s后,点F也从点B出发沿射线BC 以 的速度运动,分别连接AF,CE.设点 F运动时间为ts,其中.
(1)当t为何值时,AE=CF
(2)当t为何值时,
参考答案
刷基础
1. B【解析】∵ AD是△ABC 的高,∴AD⊥BC.∵AF∥BC,∴表示图中两条平行线之间的距离的是AD的长.
2. C 【解析】如图(1)(2),有两种情况:(1)直线a与c之间的距离是3+5=8(cm);(2)直线a与c之间的距离是5-3=2(cm).
3. B【解析】∵四边形ABCD为平行四边形,∴BC=AD=5.∵AC⊥BC,∴△ACB是直角三
角形,∴ 故选B.
4. A 【解析】 A不确定两个阴影部分的交点位置,所以无法判断阴影部分面积是否等于平行四边形面积的一半;B因为两个阴影部分的底与平行四边形的底相同,高之和正好等于平行四边形的高,所以阴影部分的面积等于平行四边形的面积的一半;C根据平行四边形的中心对称性,可知最小阴影三角形的面积等于对应的最小空白三角形的面积,所以阴影部分的面积等于平行四边形的面积的一半;D因为三个阴影部分的高与平行四边形的相等,底之和等于平行四边形的底,所以阴影部分的面积等于平行四边形的面积的一半.
【解析】如图,过点B作BE⊥CD于点 E.
∵四边形ABCD是平行四边AB形,∠A=45°,∴AB∥CD,∠C=45°,∴△BEC是等腰直角三角形,∴ BE= CE,BE +CE =BC ,即2BE =BC .∵BC=2,∴2BE =4,可得(负值舍去),则AB与CD之间的距离为
6.5 【解析】∵ ∥
7. 【解析】∵在三角形ABC中,∠A=90°,AB=3,AC=4,∴BC=5,∴点A到BC的距离为 点A到DE的距离是1,DE∥BC,∴DE与BC之间的距离是
8.【解】线段 EH的长是两条平行线AD,BC之间的距离.
理由:∵AD∥BC,AB∥EF,∴四边形ABFE是平行四边形,∴AB=EF.同理,EG=DC.
∵AB=DC,∴EF=EG.∵EH平分∠FEG,∴EH⊥BC,∴线段 EH的长是两条平行线AD,BC之间的距离.
9.【解】(1)分两种情况讨论:①点F在点C的左侧时,AE=CF,则 解得t= ②当点 F在点 C的右侧时,AE=CF,则解得 综上,当t的值为 或 时,AE=CF.
(2)∵AG∥BC,∴AG与BC之间的距离处处相等,∴当BF+AE21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
1 平行四边形的性质
第3课时 两条平行线之间的距离
刷基础
知识点 平行线间的距离
1.如图,AD,CE是△ABC的高,过点 A 作AF∥BC,则下列线段的长可表示图中两条平行线之间的距离的是( )
A. AB B. AD C. CE D. AC
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c之间的距离是( )
A.2cm B.8cm C.8cm 或2cm D.不能确定
3.如图,在平行四边形ABCD中,AB=13,AD=5,AC⊥BC,则平行四边形ABCD的面积为( )
A.30 B.60 C.65
4.下列平行四边形中,其图中阴影部分面积不一定等于平行四边形面积一半的是( )
5如图,在 ABCD中,∠A=45°,BC=2,则 AB 与 CD之间的距离为____________.
第5题图 第6题图 第7题图
6.如图,AD∥BC,AC,BD交于点E,三角形ABE的面积等于2,三角形CBE的面积等于3,那么三角形DBC的面积等于__________.
7.如图,在直角三角形ABC中,∠A=90°,AB=3,AC=4,DE∥BC,点A到DE的距离是1,则DE
与BC之间的距离是____________.
8.如图,已知AD∥BC,AB∥EF,CD∥EG,且点E和点 F,H,G分别在直线AD,BC上,EH平分 ∠FEG,AB=DC,线段EH的长是不是两条平行线AD,BC之间的距离 为什么
9.如图,在△ABC中,BC=6cm.射线AG∥BC,点E从点 A出发沿射线AG 以2cm /s的速度运动,当点E先出发1s后,点F也从点B出发沿射线BC 以 的速度运动,分别连接AF,CE.设点 F运动时间为ts,其中.
(1)当t为何值时,AE=CF
(2)当t为何值时,
参考答案
刷基础
1. B【解析】∵ AD是△ABC 的高,∴AD⊥BC.∵AF∥BC,∴表示图中两条平行线之间的距离的是AD的长.
2. C 【解析】如图(1)(2),有两种情况:(1)直线a与c之间的距离是3+5=8(cm);(2)直线a与c之间的距离是5-3=2(cm).
3. B【解析】∵四边形ABCD为平行四边形,∴BC=AD=5.∵AC⊥BC,∴△ACB是直角三
角形,∴ 故选B.
4. A 【解析】 A不确定两个阴影部分的交点位置,所以无法判断阴影部分面积是否等于平行四边形面积的一半;B因为两个阴影部分的底与平行四边形的底相同,高之和正好等于平行四边形的高,所以阴影部分的面积等于平行四边形的面积的一半;C根据平行四边形的中心对称性,可知最小阴影三角形的面积等于对应的最小空白三角形的面积,所以阴影部分的面积等于平行四边形的面积的一半;D因为三个阴影部分的高与平行四边形的相等,底之和等于平行四边形的底,所以阴影部分的面积等于平行四边形的面积的一半.
【解析】如图,过点B作BE⊥CD于点 E.
∵四边形ABCD是平行四边AB形,∠A=45°,∴AB∥CD,∠C=45°,∴△BEC是等腰直角三角形,∴ BE= CE,BE +CE =BC ,即2BE =BC .∵BC=2,∴2BE =4,可得(负值舍去),则AB与CD之间的距离为
6.5 【解析】∵ ∥
7. 【解析】∵在三角形ABC中,∠A=90°,AB=3,AC=4,∴BC=5,∴点A到BC的距离为 点A到DE的距离是1,DE∥BC,∴DE与BC之间的距离是
8.【解】线段 EH的长是两条平行线AD,BC之间的距离.
理由:∵AD∥BC,AB∥EF,∴四边形ABFE是平行四边形,∴AB=EF.同理,EG=DC.
∵AB=DC,∴EF=EG.∵EH平分∠FEG,∴EH⊥BC,∴线段 EH的长是两条平行线AD,BC之间的距离.
9.【解】(1)分两种情况讨论:①点F在点C的左侧时,AE=CF,则 解得t= ②当点 F在点 C的右侧时,AE=CF,则解得 综上,当t的值为 或 时,AE=CF.
(2)∵AG∥BC,∴AG与BC之间的距离处处相等,∴当BF+AE
21世纪教育网(www.21cnjy.com)
