5.2平行四边形的判定 第1课时 根据边的关系判定平行四边形(含答案)
文档属性
| 名称 | 5.2平行四边形的判定 第1课时 根据边的关系判定平行四边形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
2 平行四边形的判定
第1课时 根据边的关系判定平行四边形
刷基础
知识点1 用两组对边分别平行判定平行四边形
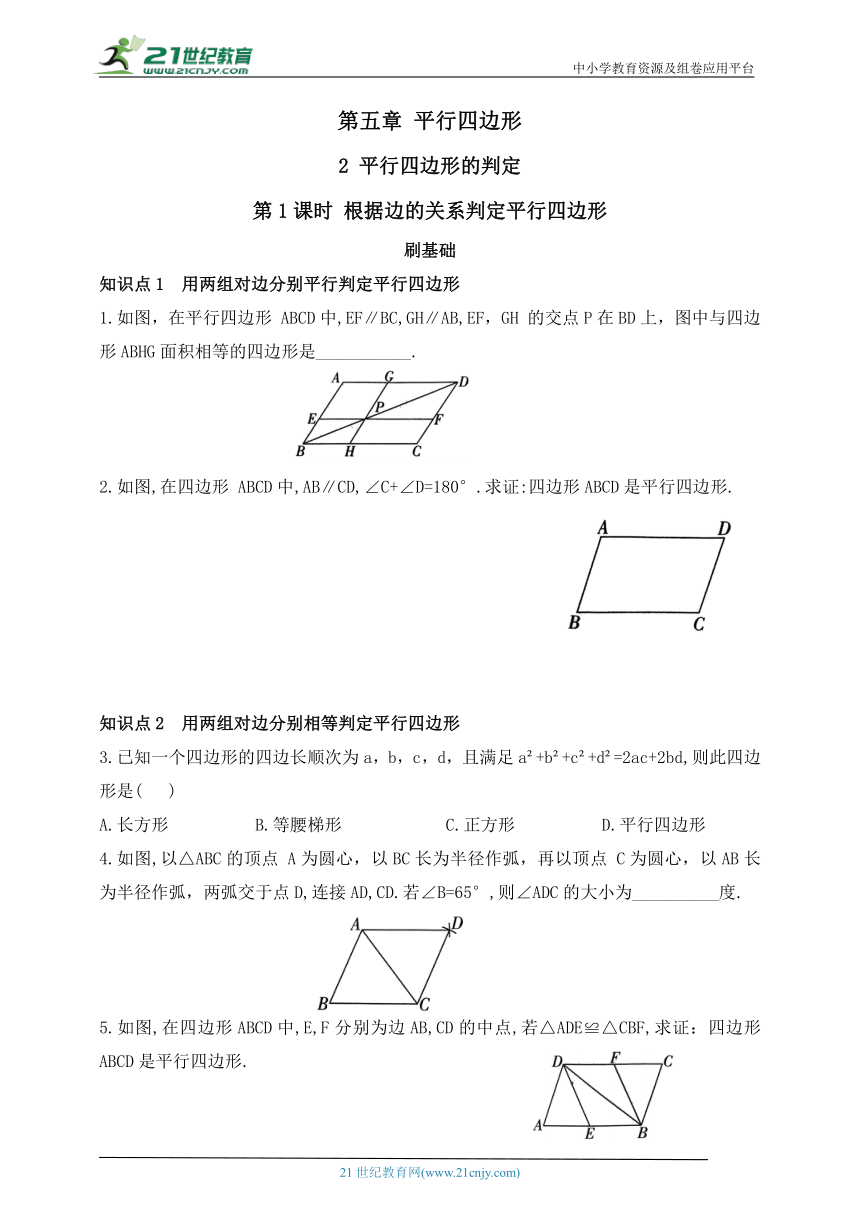
1.如图,在平行四边形 ABCD中,EF∥BC,GH∥AB,EF,GH 的交点P在BD上,图中与四边形ABHG面积相等的四边形是___________.
2.如图,在四边形 ABCD中,AB∥CD,∠C+∠D=180°.求证:四边形ABCD是平行四边形.
知识点2 用两组对边分别相等判定平行四边形
3.已知一个四边形的四边长顺次为a,b,c,d,且满足a +b +c +d =2ac+2bd,则此四边形是( )
A.长方形 B.等腰梯形 C.正方形 D.平行四边形
4.如图,以△ABC的顶点 A为圆心,以BC长为半径作弧,再以顶点 C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC的大小为__________度.
5.如图,在四边形ABCD中,E,F分别为边AB,CD的中点,若△ADE≌△CBF,求证:四边形 ABCD是平行四边形.
知识点3 用一组对边平行且相等判定平行四边形
6.如图,下列四组条件中,不能判定四边形ABCD 是平行四边形的是( )
A. AB=CD,AD=BC B. AB∥CD,AB=CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
7.如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD.求证:四边形ABED是平行四边形.
刷易错
易错点 混淆平行四边形的判定条件而出错
8.顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD,②BC=AD,③∠A=∠C,④∠B=∠D四个条件中任取其中两个,可以得出“四边形 ABCD是平行四边形”这一结论的情况共有( )
A.2种 B.3种 C.4种 D.5种
刷提升
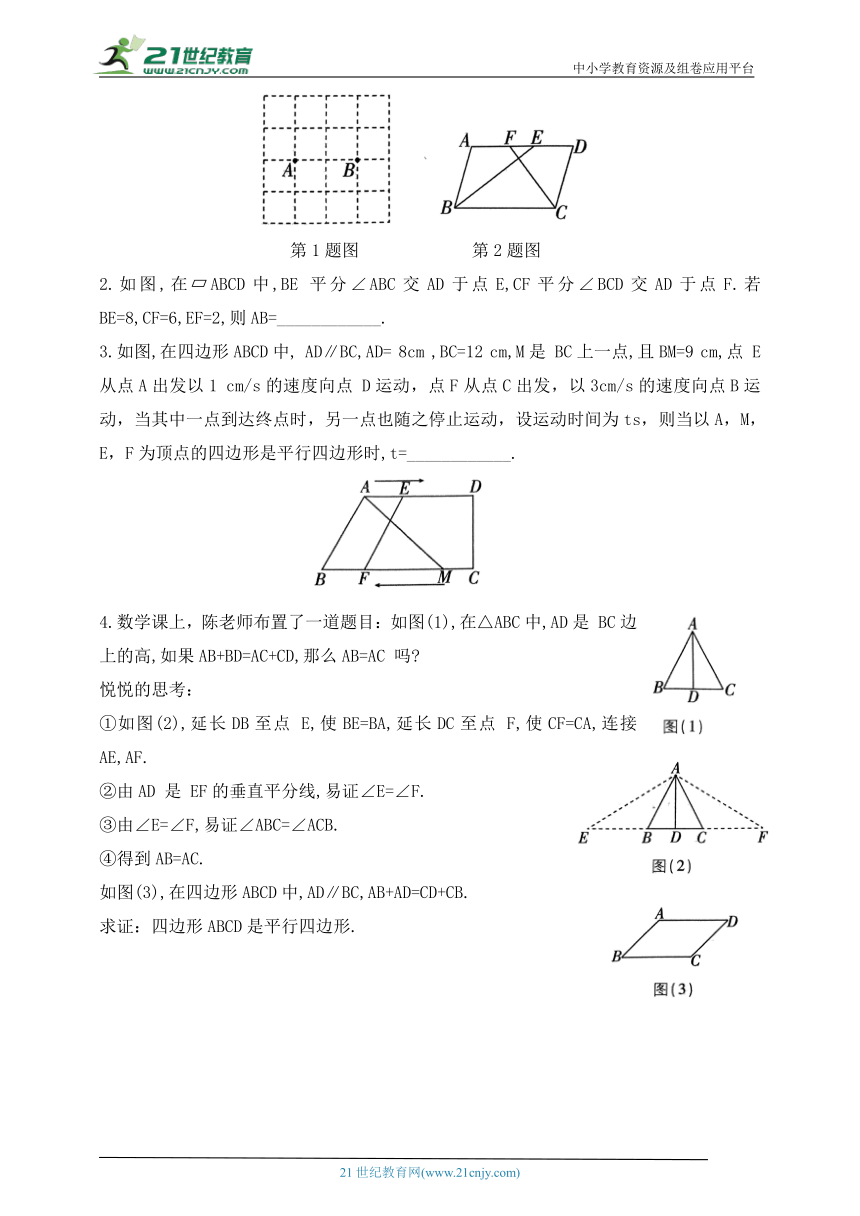
1.如图是4×4 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点叫格点,点A,B(均在格点上)的位置如图.若以A,B为顶点画面积为2 的格点平行四边形,则符合条件的平行四边形的个数为( )
A.6 B.7 C.9 D.11
第1题图 第2题图
2.如图,在 ABCD中,BE 平分∠ABC交AD于点E,CF平分∠BCD交AD于点F.若BE=8,CF=6,EF=2,则AB=____________.
3.如图,在四边形ABCD中, AD∥BC,AD= 8cm ,BC=12 cm,M是 BC上一点,且BM=9 cm,点 E从点A出发以1 cm/s的速度向点 D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为ts,则当以A,M,E,F为顶点的四边形是平行四边形时,t=____________.
4.数学课上,陈老师布置了一道题目:如图(1),在△ABC中,AD是 BC边上的高,如果AB+BD=AC+CD,那么AB=AC 吗
悦悦的思考:
①如图(2),延长DB至点 E,使BE=BA,延长DC至点 F,使CF=CA,连接AE,AF.
②由AD 是 EF的垂直平分线,易证∠E=∠F.
③由∠E=∠F,易证∠ABC=∠ACB.
④得到AB=AC.
如图(3),在四边形ABCD中,AD∥BC,AB+AD=CD+CB.
求证:四边形ABCD是平行四边形.
刷素养
5.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点 F分别作PF∥AC交AB于点F,PE∥AB交BC于点D,交AC于点 E.
(1)如图(1),当点P在BC边上时,请探索线段PE,PF,AB之间的数量关系,并证明你的结论.
(2)如图(2),当点P在△ABC内部时,线段PD,PE,PF,AB之间有怎样的数量关系 请说明理由.
(3)如图(3),当点P在△ABC外部时,线段PD,PE,PF,AB之间有怎样的数量关系 直接写出结论.
参考答案
刷基础
1.四边形BCFE【解析】∵四边形ABCD是平行四边形,∴∥∥∵EF∥BC,GH∥AB,∴EF∥BC∥AD,GH∥AB∥CD,∴四边形 GPFD,四边形EBHP,四边形AEPG,四边形 BCFE,四边形 CHPF,四边形ABHG都是平行四边形,
故答案为四边形 BCFE.
2.【证明】∵∠C+∠D=180°,∴AD∥BC.又∵AB∥CD,∴四边形ABCD是平行四边形.
3. D【解析】根据a +b +c +d =2ac+2bd,整理得(a-c) +(b-d) =0,那么a=c,b=d,所以此四边形是平行四边形. 故选 D.
4.65【解析】由作图知四边形 ABCD的两组对边分别相等,所以四边形ABCD为平行四边形,所以∠ADC=∠B=65°.
5.【证明】∵△ADE≌△CBF,∴AD=BC,AE=CF.
∵E,F分别为边AB,CD的中点,∴AB=2AE,CD=2CF,
∴AB=CD,∴四边形ABCD 是平行四边形.
6. C【解析】A选项,根据两组对边分别相等的四边形是平行四边形可判定四边形 ABCD为平行四边形,故A选项不合题意;B选项,根据一组对边平行且相等的四边形是平行四边形可判定四边形 ABCD 为平行四边形,故B选项不合题意;C 选项,不能判定四边形ABCD是平行四边形,故C选项符合题意;D选项,根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形,故D选项不合题意.故选C.
7.【证明】∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F.
∵BE=CF,∴BE+CE=CF+CE,∴BC=EF.
在△ABC和△DEF中 ∴△ABC≌△DEF(ASA),∴AB=DE.
又∵AB∥DE,∴四边形ABED是平行四边形.
刷易错
8. B【解析】由①AB∥CD,得∠A+∠D=180°.若③∠A=∠C,则∠C+∠D=180°,∴AD∥BC,
∴四边形ABCD 是平行四边形.故①③符合题意.由①AB∥CD,得∠A+∠D=180°.
若④∠B=∠D,则∠A+∠B=180°,∴AD∥BC,∴四边形ABCD是平行四边形. 故①④符合题意.由③∠A=∠C,④∠B=∠D,且∠A+∠B+∠C+∠D=360°,得∠A+∠B=180°,∠A+∠D=180°,∴AD∥BC,AB∥CD,∴ 四边形ABCD是平行四边形. 故③④符合题意. 故符合题意的有3种.故选B.
刷提升
1. D【解析】当 AB为边时,有6种情况,如图(1),当AB为对角线时,有5种情况,如图(2),所以共有11种情况符合以A,B为顶点的面积为2 的格点平行四边形.
2.5【解析】如图,过点 E作EG∥FC交BC 延长线于点G.
∵四边形ABCD 是平行四边形,∴AD∥BC,∴∠AEB=∠EBC.
∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AE= AB,同理可证 DC= DF.
∵AB∥DC,∴∠ABC+∠DCB=180°.
∵BE 平分∠ABC,CF平分 ∴∠BHC=90°,∴BE⊥CF.
∵EG∥FC,∴BE⊥EG.∵EF∥CG,∴四边形EFCG是平行四边形,∴EG=FC.
在△BEG中,BE=8,EG=CF=6,根据勾股定理,得
∵AB=AE= CD=DF,EF=CG=2,AD=BC,∴BG=BC+CG=AE+DE+CG=AE+DF-EF+EF=2AB,
∴10=2AB,∴AB=5.故答案为5.
3. 或 【解析】①当点F在线段 BM 上,AE=FM时,以A,M,E,F为顶点的四边形是平行四边形,则有t=9+3t-12,解得
②当点F在线段 CM上,AE=FM 时,以A,M,E,F为顶点的四边形是平行四边形,则有t=12-9-3t,解得
综上所述, 或 时,以A,M,E,F为顶点的四边形是平行四边形.
4.【证明】如图,在DA的延长线上取点 M,使AM=AB,在BC的延长线上取点N,使 CN=
CD,连接BM,DN,
则∠M=∠ABM,∠N=∠CDN.
∵AB+AD=CD+CB,且AM=AB,CN=CD,∴AM+AD=CN+CB,即DM=BN.
又∵AD∥BC,∴四边形MBND是平行四边形,∴MB=ND,∠M=∠N,∴∠ABM=∠CDN,
∴△ABM≌△CDN(ASA),∴AM=CN.
∵DM=BN,∴DM-AM=BN-CN,即AD=BC.
∵AD∥BC,∴四边形 ABCD 是平行四边形.
刷素养
5.(1)【解】(1)PE+PF=AB.证明:∵PF∥AC,PE∥AB,∴四边形 FPEA为平行四边形,∴PF=
AE,PE=AF.∵PF∥AC,∴∠FPB=∠C.∵AB=AC,∴∠B=∠C,∴∠FPB=∠B,∴BF=FP,
∴AB=AF+FB=PE+FP,∴PE+PF=AB.
(2)PD+PE+PF=AB.理由:∵PF∥AC,PE∥AB,∴四边形 FPEA为平行四边形,∴PF=AE,PE=AF.∵PE∥AB,∴∠B=∠EDC.∵∠B=∠C,∴∠EDC=∠C,∴ED=EC,∴AB=AC=AE+EC=FP+ED=PF+PD+PE,∴PD+PE+PF=AB.
(3)PE+PF-PD=AB.证明:∵PF∥AC,PE∥AB,∴四边形 FPEA 为平行四边形,∴ PF=AE,PE=AF.∵PE∥AB,∴∠B=∠EDC.∵∠B=∠C,∴∠EDC=∠C,∴ED=EC,∴AB=AC=AE+EC=PF+ED=PF+PE-PD,∴PE+PF-PD=AB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
2 平行四边形的判定
第1课时 根据边的关系判定平行四边形
刷基础
知识点1 用两组对边分别平行判定平行四边形
1.如图,在平行四边形 ABCD中,EF∥BC,GH∥AB,EF,GH 的交点P在BD上,图中与四边形ABHG面积相等的四边形是___________.
2.如图,在四边形 ABCD中,AB∥CD,∠C+∠D=180°.求证:四边形ABCD是平行四边形.
知识点2 用两组对边分别相等判定平行四边形
3.已知一个四边形的四边长顺次为a,b,c,d,且满足a +b +c +d =2ac+2bd,则此四边形是( )
A.长方形 B.等腰梯形 C.正方形 D.平行四边形
4.如图,以△ABC的顶点 A为圆心,以BC长为半径作弧,再以顶点 C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC的大小为__________度.
5.如图,在四边形ABCD中,E,F分别为边AB,CD的中点,若△ADE≌△CBF,求证:四边形 ABCD是平行四边形.
知识点3 用一组对边平行且相等判定平行四边形
6.如图,下列四组条件中,不能判定四边形ABCD 是平行四边形的是( )
A. AB=CD,AD=BC B. AB∥CD,AB=CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
7.如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD.求证:四边形ABED是平行四边形.
刷易错
易错点 混淆平行四边形的判定条件而出错
8.顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD,②BC=AD,③∠A=∠C,④∠B=∠D四个条件中任取其中两个,可以得出“四边形 ABCD是平行四边形”这一结论的情况共有( )
A.2种 B.3种 C.4种 D.5种
刷提升
1.如图是4×4 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点叫格点,点A,B(均在格点上)的位置如图.若以A,B为顶点画面积为2 的格点平行四边形,则符合条件的平行四边形的个数为( )
A.6 B.7 C.9 D.11
第1题图 第2题图
2.如图,在 ABCD中,BE 平分∠ABC交AD于点E,CF平分∠BCD交AD于点F.若BE=8,CF=6,EF=2,则AB=____________.
3.如图,在四边形ABCD中, AD∥BC,AD= 8cm ,BC=12 cm,M是 BC上一点,且BM=9 cm,点 E从点A出发以1 cm/s的速度向点 D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为ts,则当以A,M,E,F为顶点的四边形是平行四边形时,t=____________.
4.数学课上,陈老师布置了一道题目:如图(1),在△ABC中,AD是 BC边上的高,如果AB+BD=AC+CD,那么AB=AC 吗
悦悦的思考:
①如图(2),延长DB至点 E,使BE=BA,延长DC至点 F,使CF=CA,连接AE,AF.
②由AD 是 EF的垂直平分线,易证∠E=∠F.
③由∠E=∠F,易证∠ABC=∠ACB.
④得到AB=AC.
如图(3),在四边形ABCD中,AD∥BC,AB+AD=CD+CB.
求证:四边形ABCD是平行四边形.
刷素养
5.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点 F分别作PF∥AC交AB于点F,PE∥AB交BC于点D,交AC于点 E.
(1)如图(1),当点P在BC边上时,请探索线段PE,PF,AB之间的数量关系,并证明你的结论.
(2)如图(2),当点P在△ABC内部时,线段PD,PE,PF,AB之间有怎样的数量关系 请说明理由.
(3)如图(3),当点P在△ABC外部时,线段PD,PE,PF,AB之间有怎样的数量关系 直接写出结论.
参考答案
刷基础
1.四边形BCFE【解析】∵四边形ABCD是平行四边形,∴∥∥∵EF∥BC,GH∥AB,∴EF∥BC∥AD,GH∥AB∥CD,∴四边形 GPFD,四边形EBHP,四边形AEPG,四边形 BCFE,四边形 CHPF,四边形ABHG都是平行四边形,
故答案为四边形 BCFE.
2.【证明】∵∠C+∠D=180°,∴AD∥BC.又∵AB∥CD,∴四边形ABCD是平行四边形.
3. D【解析】根据a +b +c +d =2ac+2bd,整理得(a-c) +(b-d) =0,那么a=c,b=d,所以此四边形是平行四边形. 故选 D.
4.65【解析】由作图知四边形 ABCD的两组对边分别相等,所以四边形ABCD为平行四边形,所以∠ADC=∠B=65°.
5.【证明】∵△ADE≌△CBF,∴AD=BC,AE=CF.
∵E,F分别为边AB,CD的中点,∴AB=2AE,CD=2CF,
∴AB=CD,∴四边形ABCD 是平行四边形.
6. C【解析】A选项,根据两组对边分别相等的四边形是平行四边形可判定四边形 ABCD为平行四边形,故A选项不合题意;B选项,根据一组对边平行且相等的四边形是平行四边形可判定四边形 ABCD 为平行四边形,故B选项不合题意;C 选项,不能判定四边形ABCD是平行四边形,故C选项符合题意;D选项,根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形,故D选项不合题意.故选C.
7.【证明】∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F.
∵BE=CF,∴BE+CE=CF+CE,∴BC=EF.
在△ABC和△DEF中 ∴△ABC≌△DEF(ASA),∴AB=DE.
又∵AB∥DE,∴四边形ABED是平行四边形.
刷易错
8. B【解析】由①AB∥CD,得∠A+∠D=180°.若③∠A=∠C,则∠C+∠D=180°,∴AD∥BC,
∴四边形ABCD 是平行四边形.故①③符合题意.由①AB∥CD,得∠A+∠D=180°.
若④∠B=∠D,则∠A+∠B=180°,∴AD∥BC,∴四边形ABCD是平行四边形. 故①④符合题意.由③∠A=∠C,④∠B=∠D,且∠A+∠B+∠C+∠D=360°,得∠A+∠B=180°,∠A+∠D=180°,∴AD∥BC,AB∥CD,∴ 四边形ABCD是平行四边形. 故③④符合题意. 故符合题意的有3种.故选B.
刷提升
1. D【解析】当 AB为边时,有6种情况,如图(1),当AB为对角线时,有5种情况,如图(2),所以共有11种情况符合以A,B为顶点的面积为2 的格点平行四边形.
2.5【解析】如图,过点 E作EG∥FC交BC 延长线于点G.
∵四边形ABCD 是平行四边形,∴AD∥BC,∴∠AEB=∠EBC.
∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AE= AB,同理可证 DC= DF.
∵AB∥DC,∴∠ABC+∠DCB=180°.
∵BE 平分∠ABC,CF平分 ∴∠BHC=90°,∴BE⊥CF.
∵EG∥FC,∴BE⊥EG.∵EF∥CG,∴四边形EFCG是平行四边形,∴EG=FC.
在△BEG中,BE=8,EG=CF=6,根据勾股定理,得
∵AB=AE= CD=DF,EF=CG=2,AD=BC,∴BG=BC+CG=AE+DE+CG=AE+DF-EF+EF=2AB,
∴10=2AB,∴AB=5.故答案为5.
3. 或 【解析】①当点F在线段 BM 上,AE=FM时,以A,M,E,F为顶点的四边形是平行四边形,则有t=9+3t-12,解得
②当点F在线段 CM上,AE=FM 时,以A,M,E,F为顶点的四边形是平行四边形,则有t=12-9-3t,解得
综上所述, 或 时,以A,M,E,F为顶点的四边形是平行四边形.
4.【证明】如图,在DA的延长线上取点 M,使AM=AB,在BC的延长线上取点N,使 CN=
CD,连接BM,DN,
则∠M=∠ABM,∠N=∠CDN.
∵AB+AD=CD+CB,且AM=AB,CN=CD,∴AM+AD=CN+CB,即DM=BN.
又∵AD∥BC,∴四边形MBND是平行四边形,∴MB=ND,∠M=∠N,∴∠ABM=∠CDN,
∴△ABM≌△CDN(ASA),∴AM=CN.
∵DM=BN,∴DM-AM=BN-CN,即AD=BC.
∵AD∥BC,∴四边形 ABCD 是平行四边形.
刷素养
5.(1)【解】(1)PE+PF=AB.证明:∵PF∥AC,PE∥AB,∴四边形 FPEA为平行四边形,∴PF=
AE,PE=AF.∵PF∥AC,∴∠FPB=∠C.∵AB=AC,∴∠B=∠C,∴∠FPB=∠B,∴BF=FP,
∴AB=AF+FB=PE+FP,∴PE+PF=AB.
(2)PD+PE+PF=AB.理由:∵PF∥AC,PE∥AB,∴四边形 FPEA为平行四边形,∴PF=AE,PE=AF.∵PE∥AB,∴∠B=∠EDC.∵∠B=∠C,∴∠EDC=∠C,∴ED=EC,∴AB=AC=AE+EC=FP+ED=PF+PD+PE,∴PD+PE+PF=AB.
(3)PE+PF-PD=AB.证明:∵PF∥AC,PE∥AB,∴四边形 FPEA 为平行四边形,∴ PF=AE,PE=AF.∵PE∥AB,∴∠B=∠EDC.∵∠B=∠C,∴∠EDC=∠C,∴ED=EC,∴AB=AC=AE+EC=PF+ED=PF+PE-PD,∴PE+PF-PD=AB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
