5.3 三角形的中位线(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
3 三角形的中位线
刷基础
知识点1 一条中位线问题
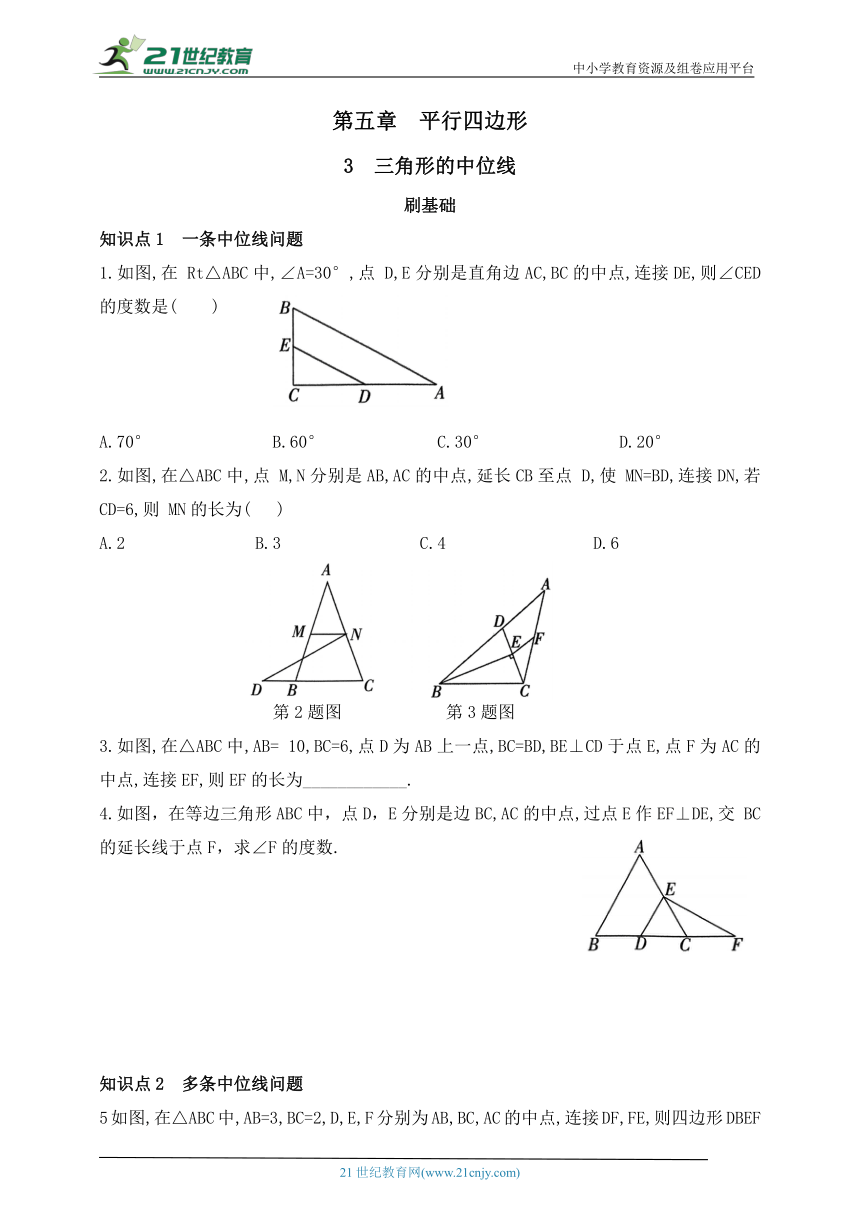
1.如图,在 Rt△ABC中,∠A=30°,点 D,E分别是直角边AC,BC的中点,连接DE,则∠CED的度数是( )
A.70° B.60° C.30° D.20°
2.如图,在△ABC中,点 M,N分别是AB,AC的中点,延长CB至点 D,使 MN=BD,连接DN,若CD=6,则 MN的长为( )
A.2 B.3 C.4 D.6
第2题图 第3题图
3.如图,在△ABC中,AB= 10,BC=6,点D为AB上一点,BC=BD,BE⊥CD于点E,点F为AC的中点,连接EF,则EF的长为____________.
4.如图,在等边三角形ABC中,点D,E分别是边BC,AC的中点,过点E作EF⊥DE,交 BC的延长线于点F,求∠F的度数.
知识点2 多条中位线问题
5如图,在△ABC中,AB=3,BC=2,D,E,F分别为AB,BC,AC的中点,连接DF,FE,则四边形DBEF的周长是( )
A.5 B.7 C.9 D.11
第5题图 第6题图
6.如图,面积为2的等边三角形ABC中,D,E,F分别是AB,BC,CA的中点,则△DEF的面积为( )
B.1
7.如图,在四边形ABCD中,E,F分别是AD,BC 的中点,点G是对角线BD的中点,连接GE,GF,EF,若AB=CD,∠ABD=20°,∠BDC=70°,则∠GEF=( )
A.25° B.30° C.45° D.35°
8.如图,四边形 ABCD中,对角线AC 与BD交于点P,AC=BD,E,F,G分别是AB,CD,BC的中点,连接EG,FG,EF,EF分别交BD,AC于M,N.求证:∠PMN=∠PNM.
刷提升
1.如图,点 G为△ABC的重心,连接CG,AG并延长分别交AB,BC于点E,F,连接EF,若AB=4.4,AC=3.4,BC=3.6,则EF的长度为( )
A.1.7 B.1.8 C.2.2 D.2.4
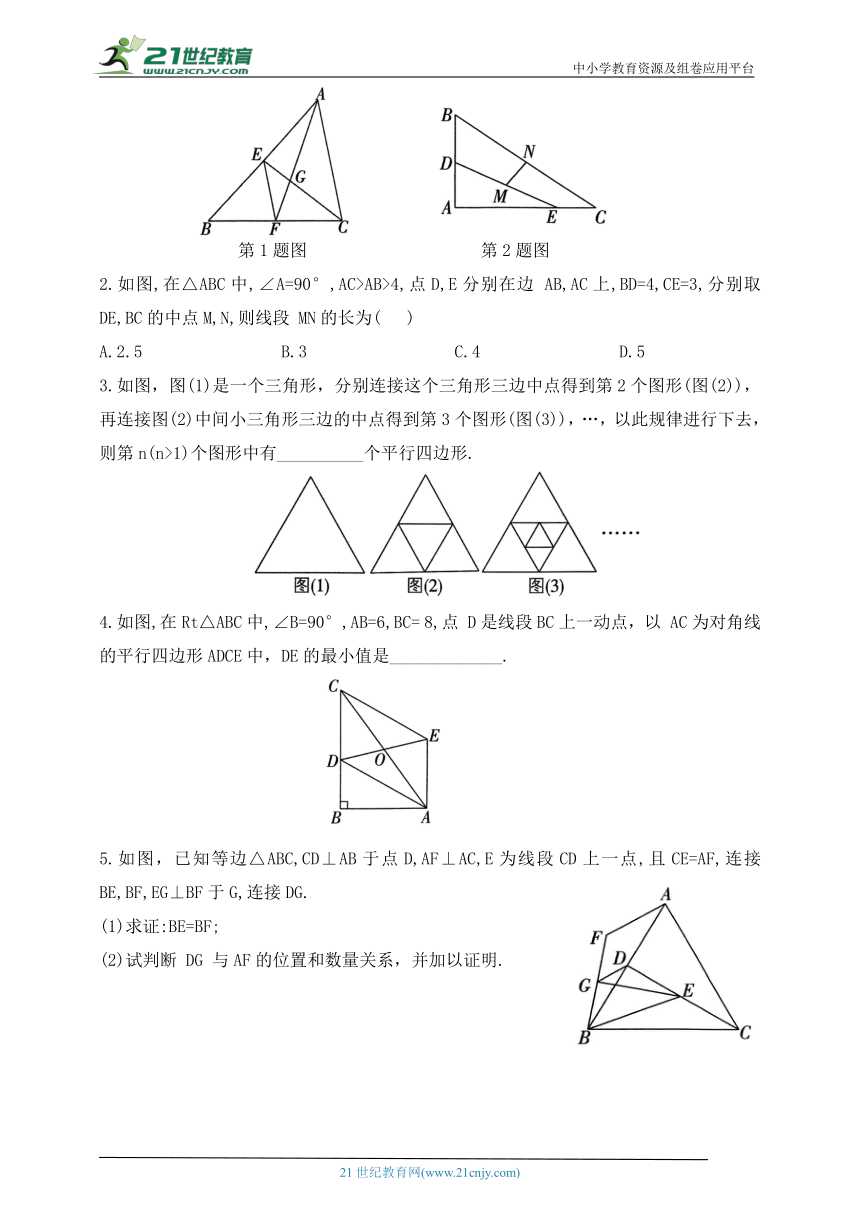
第1题图 第2题图
2.如图,在△ABC中,∠A=90°,AC>AB>4,点D,E分别在边 AB,AC上,BD=4,CE=3,分别取DE,BC的中点M,N,则线段 MN的长为( )
A.2.5 B.3 C.4 D.5
3.如图,图(1)是一个三角形,分别连接这个三角形三边中点得到第2个图形(图(2)),再连接图(2)中间小三角形三边的中点得到第3个图形(图(3)),…,以此规律进行下去,则第n(n>1)个图形中有__________个平行四边形.
4.如图,在Rt△ABC中,∠B=90°,AB=6,BC= 8,点 D是线段BC上一动点,以 AC为对角线的平行四边形ADCE中,DE的最小值是_____________.
5.如图,已知等边△ABC,CD⊥AB于点D,AF⊥AC,E为线段CD上一点,且CE=AF,连接BE,BF,EG⊥BF于G,连接DG.
(1)求证:BE=BF;
(2)试判断 DG 与AF的位置和数量关系,并加以证明.
刷素养
6.如图(1),在△ABC中,点D是边BC的中点,点 E 在△ABC内,AE平分∠BAC,CE⊥AE,点 F在边 AB上,EF∥BC.
(1)求证:四边形 BDEF是平行四边形.
(2)判断线段 BF,AB,AC之间具有怎样的数量关系 证明你所得到的结论.
(3)如图(2),点P是△ABC的边AB上的一点,若△DCE的面积. 请直接写出△DPE的面积(不需要写出解答过程).
参考答案
刷基础
1. B【解析】在 Rt△ABC 中,∠A=30°,则∠B=90°-∠A=60°.∵D,E分别是边AC,BC的中点,∴ DE 是△ABC 的中位线,∴ DE∥AB,∴∠CED=∠B=60°,故选 B.
2. A【解析】∵点M,N分别是AB,AC的中点, ∵CD=6,∴BC=4,∴MN=2.故选A.
3.2【解析】由题意得BD=BC=6,∴AD=AB-BD=4.∵BC= BD,BE⊥CD,∴ CE= ED.
又∵点F为AC的中点,∴
4.【解】∵△ABC是等边三角形,∴∠B=60°.
∵点D,E分别是边 BC,AC的中点,∴DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°.
5. A【解析】∵D,E,F分别为AB,BC,AC的中点,∴.四边形DBEF的周长为1.5+1.5+1+1=5.
6. D【解析】∵D,E,F分别是AB,BC,CA的中点,∴DF为△ABC的中位线,
∴DF∥BC,DF=
在△EDF和△DEB中 ∴△DEF≌△EDB(SAS).
同理可证得△DEF≌△CFE,△DEF≌△FAD.∵S△ABC=2,故选D.
7. A【解析】∵E,G分别是AD,BD的中点,∴EG是△ADB的中位线,∴
∥∴∠EGD=∠ABD=20°,同理可得 FG∥CD,∴ ∠DGF = 180°-∠BDC = 110°,∴∠EGF=∠EGD+∠FGD=130°.∵AB=CD,
25°,故选A.
8.【证明】∵E,F分别为AB,CD的中点,∥
∵AC=BD,∴EG=FG,∴∠GEF=∠GFE.
又∵∠GEF=∠PNM,∠GFE=∠PMN,∴∠PMN=∠PNM.
刷提升
1. A【解析】∵点 G为△ABC的重心,∴AE=BE, 故选A.
2. A 【解析】如图,作CH∥AB,连接DN并延长交CH于H,连接 EH.
∵BD∥CH,∴∠B=∠NCH,∠ECH+∠A = 180°. ∵∠A = 90°,∴∠ECH=∠A=90°.
在△DNB 和△HNC中,∴△DNB≌△HNC(ASA),
∴CH=BD=4,DN=NH.在Rt△CEH中,CH=故选A.
3.(3n-3)【解析】分别数出图(1)、图(2)、图(3)中的平行四边形的个数,图(1)中平行四边形的个数为0=3×(1-1);图(2)中平行四边形的个数为3=3×(2-1);图(3)中平行四边形的个数为6=3×(3-1); .可以发现,第n个图形中平行四边形的个数等于3与n-1的乘积,即第n个图形中共有平行四边形的个数为3n-3.故答案为(3n-3).
4.6【解析】平行四边形 ADCE的对角线的交点是AC的中点O,当OD⊥BC时,OD最小,
此时DE最小.∵OD⊥BC,BC⊥AB,∴OD∥AB.又∵OC=OA,∴OD是△ABC 的中位线,
5.(1)【证明】在等边△ABC中,∠BAC=∠ABC=∠ACB=60°,AB=BC.
∵CD⊥AB,∴AD=BD,∠ACD=∠BCD=30°.
又∵AF⊥AC,∴∠FAC=90°,∴∠FAB=30°,∴∠FAB=∠ECB=30°.
在△BEC和△BFA中, ∴△BCE≌△BAF(SAS),∴BE=BF.
∥
证明:如图,连接EF.
由BE=BF添加辅助线构造等边三角形,利用其三线合一的性质得到中点,进而利用三角形中位线定理得证.由△BCE≌△BAF可知∠CBE=∠ABF,∴∠FBE=60°.
又∵BE=BF,∴△BEF是等边三角形.∵EG⊥BF,∴FG=BG.
∵AD=BD,∴DG是△ABF的中位线, ∥
刷素养
6.(1)【证明】延长CE交AB 于点 G,如图.
∵AE⊥CE,∴∠AEG=∠AEC=90°.又∵AE平分∠BAC,∴∠GAE=∠CAE.
在△AEG和△AEC中 ∴△AEG≌△AEC(ASA),∴GE=EC.
∵点D是边 BC的中点,∴BD=CD,∴DE 为△CGB的中位线,∴DE∥AB.
又∵EF∥BC,∴四边形BDEF是平行四边形.
【解】 证明如下:
∵四边形BFED是平行四边形,∴BF=DE.
∵D,E分别是BC,GC的中点,
∵△AEG≌△AEC,∴AG=AC,
(3)△DPE的面积为3.∵ BD=DC,EF∥BC,∴△DCE中DC边上的高与 BDEF中BD边上的高相等, 设平行四边形BDEF中BF边上的高为h,则 6÷2=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
3 三角形的中位线
刷基础
知识点1 一条中位线问题
1.如图,在 Rt△ABC中,∠A=30°,点 D,E分别是直角边AC,BC的中点,连接DE,则∠CED的度数是( )
A.70° B.60° C.30° D.20°
2.如图,在△ABC中,点 M,N分别是AB,AC的中点,延长CB至点 D,使 MN=BD,连接DN,若CD=6,则 MN的长为( )
A.2 B.3 C.4 D.6
第2题图 第3题图
3.如图,在△ABC中,AB= 10,BC=6,点D为AB上一点,BC=BD,BE⊥CD于点E,点F为AC的中点,连接EF,则EF的长为____________.
4.如图,在等边三角形ABC中,点D,E分别是边BC,AC的中点,过点E作EF⊥DE,交 BC的延长线于点F,求∠F的度数.
知识点2 多条中位线问题
5如图,在△ABC中,AB=3,BC=2,D,E,F分别为AB,BC,AC的中点,连接DF,FE,则四边形DBEF的周长是( )
A.5 B.7 C.9 D.11
第5题图 第6题图
6.如图,面积为2的等边三角形ABC中,D,E,F分别是AB,BC,CA的中点,则△DEF的面积为( )
B.1
7.如图,在四边形ABCD中,E,F分别是AD,BC 的中点,点G是对角线BD的中点,连接GE,GF,EF,若AB=CD,∠ABD=20°,∠BDC=70°,则∠GEF=( )
A.25° B.30° C.45° D.35°
8.如图,四边形 ABCD中,对角线AC 与BD交于点P,AC=BD,E,F,G分别是AB,CD,BC的中点,连接EG,FG,EF,EF分别交BD,AC于M,N.求证:∠PMN=∠PNM.
刷提升
1.如图,点 G为△ABC的重心,连接CG,AG并延长分别交AB,BC于点E,F,连接EF,若AB=4.4,AC=3.4,BC=3.6,则EF的长度为( )
A.1.7 B.1.8 C.2.2 D.2.4
第1题图 第2题图
2.如图,在△ABC中,∠A=90°,AC>AB>4,点D,E分别在边 AB,AC上,BD=4,CE=3,分别取DE,BC的中点M,N,则线段 MN的长为( )
A.2.5 B.3 C.4 D.5
3.如图,图(1)是一个三角形,分别连接这个三角形三边中点得到第2个图形(图(2)),再连接图(2)中间小三角形三边的中点得到第3个图形(图(3)),…,以此规律进行下去,则第n(n>1)个图形中有__________个平行四边形.
4.如图,在Rt△ABC中,∠B=90°,AB=6,BC= 8,点 D是线段BC上一动点,以 AC为对角线的平行四边形ADCE中,DE的最小值是_____________.
5.如图,已知等边△ABC,CD⊥AB于点D,AF⊥AC,E为线段CD上一点,且CE=AF,连接BE,BF,EG⊥BF于G,连接DG.
(1)求证:BE=BF;
(2)试判断 DG 与AF的位置和数量关系,并加以证明.
刷素养
6.如图(1),在△ABC中,点D是边BC的中点,点 E 在△ABC内,AE平分∠BAC,CE⊥AE,点 F在边 AB上,EF∥BC.
(1)求证:四边形 BDEF是平行四边形.
(2)判断线段 BF,AB,AC之间具有怎样的数量关系 证明你所得到的结论.
(3)如图(2),点P是△ABC的边AB上的一点,若△DCE的面积. 请直接写出△DPE的面积(不需要写出解答过程).
参考答案
刷基础
1. B【解析】在 Rt△ABC 中,∠A=30°,则∠B=90°-∠A=60°.∵D,E分别是边AC,BC的中点,∴ DE 是△ABC 的中位线,∴ DE∥AB,∴∠CED=∠B=60°,故选 B.
2. A【解析】∵点M,N分别是AB,AC的中点, ∵CD=6,∴BC=4,∴MN=2.故选A.
3.2【解析】由题意得BD=BC=6,∴AD=AB-BD=4.∵BC= BD,BE⊥CD,∴ CE= ED.
又∵点F为AC的中点,∴
4.【解】∵△ABC是等边三角形,∴∠B=60°.
∵点D,E分别是边 BC,AC的中点,∴DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°.
5. A【解析】∵D,E,F分别为AB,BC,AC的中点,∴.四边形DBEF的周长为1.5+1.5+1+1=5.
6. D【解析】∵D,E,F分别是AB,BC,CA的中点,∴DF为△ABC的中位线,
∴DF∥BC,DF=
在△EDF和△DEB中 ∴△DEF≌△EDB(SAS).
同理可证得△DEF≌△CFE,△DEF≌△FAD.∵S△ABC=2,故选D.
7. A【解析】∵E,G分别是AD,BD的中点,∴EG是△ADB的中位线,∴
∥∴∠EGD=∠ABD=20°,同理可得 FG∥CD,∴ ∠DGF = 180°-∠BDC = 110°,∴∠EGF=∠EGD+∠FGD=130°.∵AB=CD,
25°,故选A.
8.【证明】∵E,F分别为AB,CD的中点,∥
∵AC=BD,∴EG=FG,∴∠GEF=∠GFE.
又∵∠GEF=∠PNM,∠GFE=∠PMN,∴∠PMN=∠PNM.
刷提升
1. A【解析】∵点 G为△ABC的重心,∴AE=BE, 故选A.
2. A 【解析】如图,作CH∥AB,连接DN并延长交CH于H,连接 EH.
∵BD∥CH,∴∠B=∠NCH,∠ECH+∠A = 180°. ∵∠A = 90°,∴∠ECH=∠A=90°.
在△DNB 和△HNC中,∴△DNB≌△HNC(ASA),
∴CH=BD=4,DN=NH.在Rt△CEH中,CH=故选A.
3.(3n-3)【解析】分别数出图(1)、图(2)、图(3)中的平行四边形的个数,图(1)中平行四边形的个数为0=3×(1-1);图(2)中平行四边形的个数为3=3×(2-1);图(3)中平行四边形的个数为6=3×(3-1); .可以发现,第n个图形中平行四边形的个数等于3与n-1的乘积,即第n个图形中共有平行四边形的个数为3n-3.故答案为(3n-3).
4.6【解析】平行四边形 ADCE的对角线的交点是AC的中点O,当OD⊥BC时,OD最小,
此时DE最小.∵OD⊥BC,BC⊥AB,∴OD∥AB.又∵OC=OA,∴OD是△ABC 的中位线,
5.(1)【证明】在等边△ABC中,∠BAC=∠ABC=∠ACB=60°,AB=BC.
∵CD⊥AB,∴AD=BD,∠ACD=∠BCD=30°.
又∵AF⊥AC,∴∠FAC=90°,∴∠FAB=30°,∴∠FAB=∠ECB=30°.
在△BEC和△BFA中, ∴△BCE≌△BAF(SAS),∴BE=BF.
∥
证明:如图,连接EF.
由BE=BF添加辅助线构造等边三角形,利用其三线合一的性质得到中点,进而利用三角形中位线定理得证.由△BCE≌△BAF可知∠CBE=∠ABF,∴∠FBE=60°.
又∵BE=BF,∴△BEF是等边三角形.∵EG⊥BF,∴FG=BG.
∵AD=BD,∴DG是△ABF的中位线, ∥
刷素养
6.(1)【证明】延长CE交AB 于点 G,如图.
∵AE⊥CE,∴∠AEG=∠AEC=90°.又∵AE平分∠BAC,∴∠GAE=∠CAE.
在△AEG和△AEC中 ∴△AEG≌△AEC(ASA),∴GE=EC.
∵点D是边 BC的中点,∴BD=CD,∴DE 为△CGB的中位线,∴DE∥AB.
又∵EF∥BC,∴四边形BDEF是平行四边形.
【解】 证明如下:
∵四边形BFED是平行四边形,∴BF=DE.
∵D,E分别是BC,GC的中点,
∵△AEG≌△AEC,∴AG=AC,
(3)△DPE的面积为3.∵ BD=DC,EF∥BC,∴△DCE中DC边上的高与 BDEF中BD边上的高相等, 设平行四边形BDEF中BF边上的高为h,则 6÷2=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
