第五章 平行四边形 专题 构造中位线的方法(含答案)
文档属性
| 名称 | 第五章 平行四边形 专题 构造中位线的方法(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 08:23:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
专题 构造中位线的方法
类型1 取一边中点构造三角形的中位线
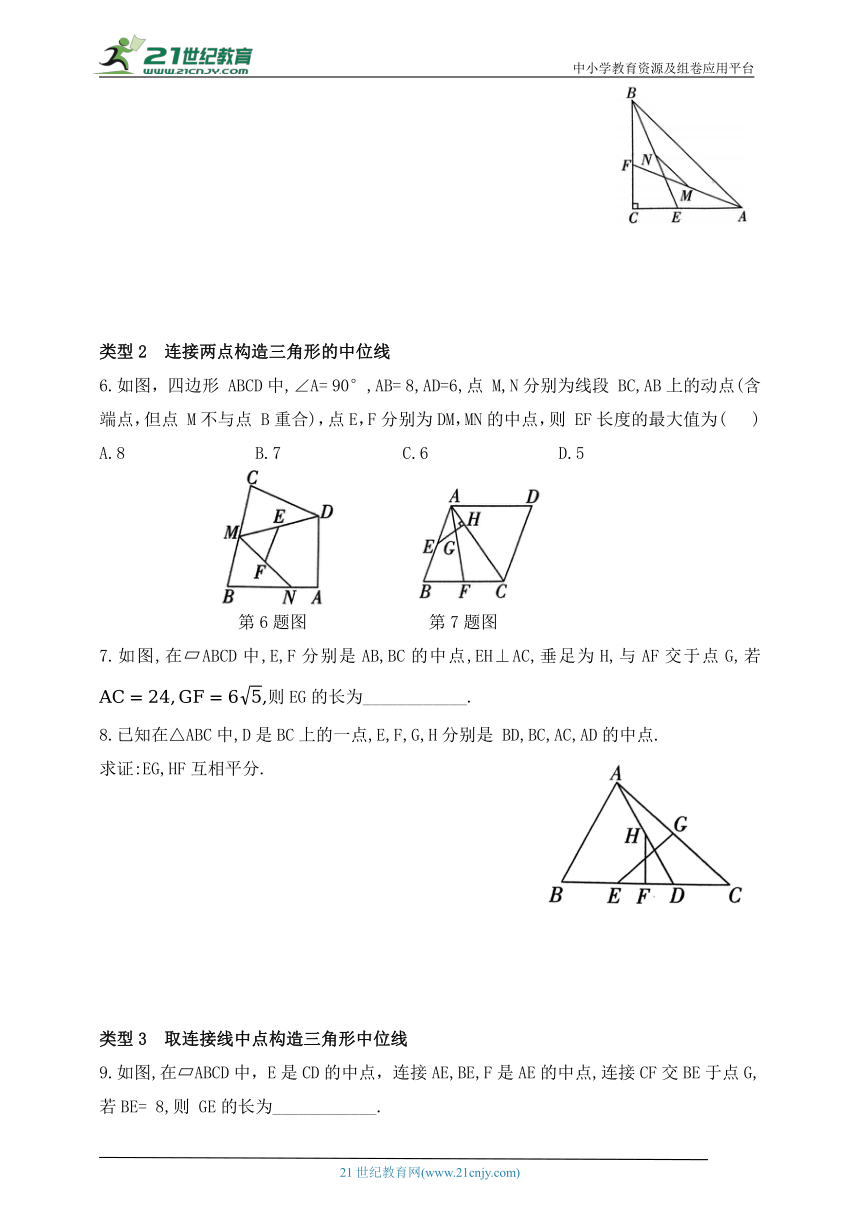
1.如图,在△ABC中,延长BC至D,使得 过AC 中点 E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
A.3 B.4
第1题图 第2题图
2.如图,DE 是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12 cm ,则 的值为( )
A.4 cm B.6cm C.8cm D.9 cm
3.如图,在四边形 ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2.对于MN的长,给出了四种猜测:①MN=4;②MN=3;③MN=2;④MN=1.猜测正确的是( )
A.① B.② C.③ D.④
第3题图 第4题图
4.如图,AD是△ABC的中线,M是AD的中点,连接BM并延长交AC于点 N,若AC=4,则AN=___________.
5.如图,在△ABC中,∠C=90°,CA= CB,E,F分别为CA,CB上一点,且CE= CF,M,N分别为AF,BE的中点,求证:AE =2MN .
类型2 连接两点构造三角形的中位线
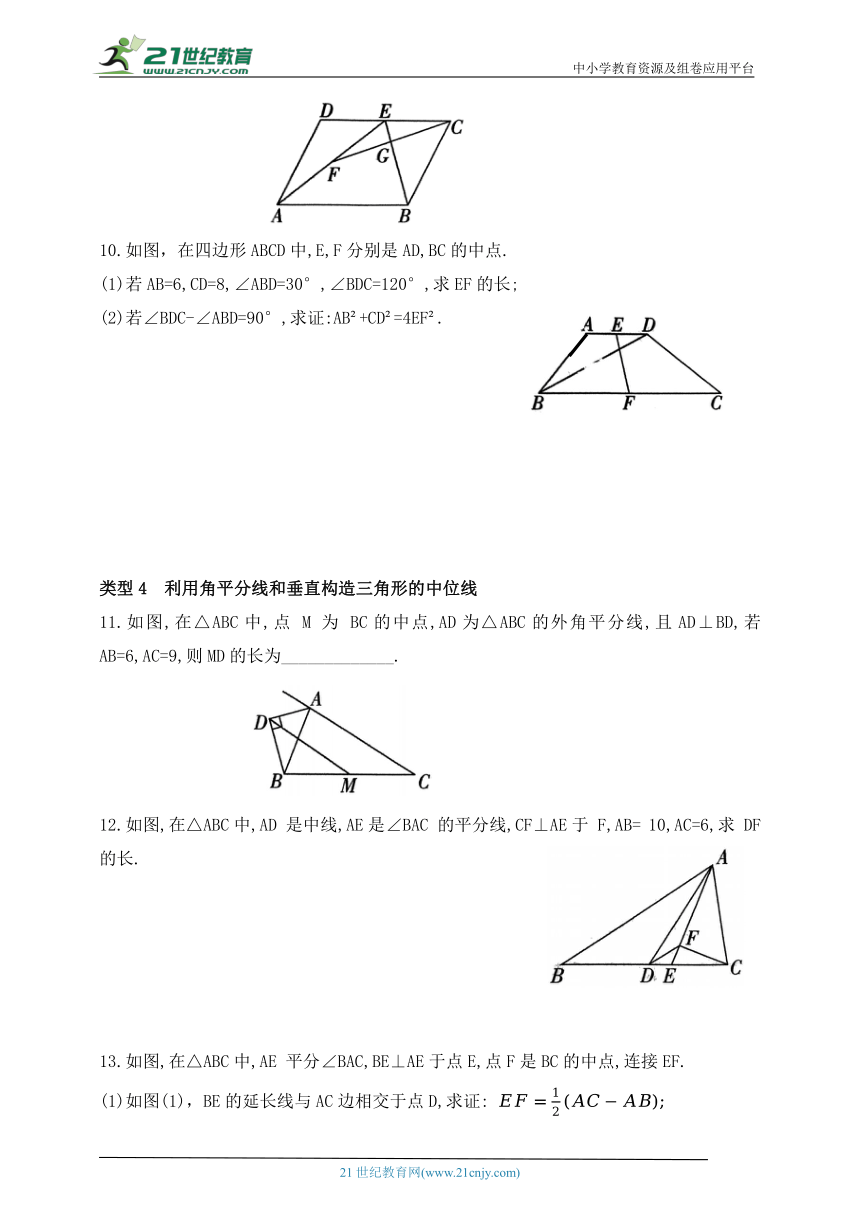
6.如图,四边形 ABCD中,∠A= 90°,AB= 8,AD=6,点 M,N分别为线段 BC,AB上的动点(含端点,但点 M不与点 B重合),点E,F分别为DM,MN的中点,则 EF长度的最大值为( )
A.8 B.7 C.6 D.5
第6题图 第7题图
7.如图,在 ABCD中,E,F分别是AB,BC的中点,EH⊥AC,垂足为H,与AF交于点G,若 则EG的长为____________.
8.已知在△ABC中,D是BC上的一点,E,F,G,H分别是 BD,BC,AC,AD的中点.
求证:EG,HF互相平分.
类型3 取连接线中点构造三角形中位线
9.如图,在 ABCD中,E是CD的中点,连接AE,BE,F是AE的中点,连接CF交BE于点G,若BE= 8,则 GE的长为____________.
10.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC-∠ABD=90°,求证:AB +CD =4EF .
类型4 利用角平分线和垂直构造三角形的中位线
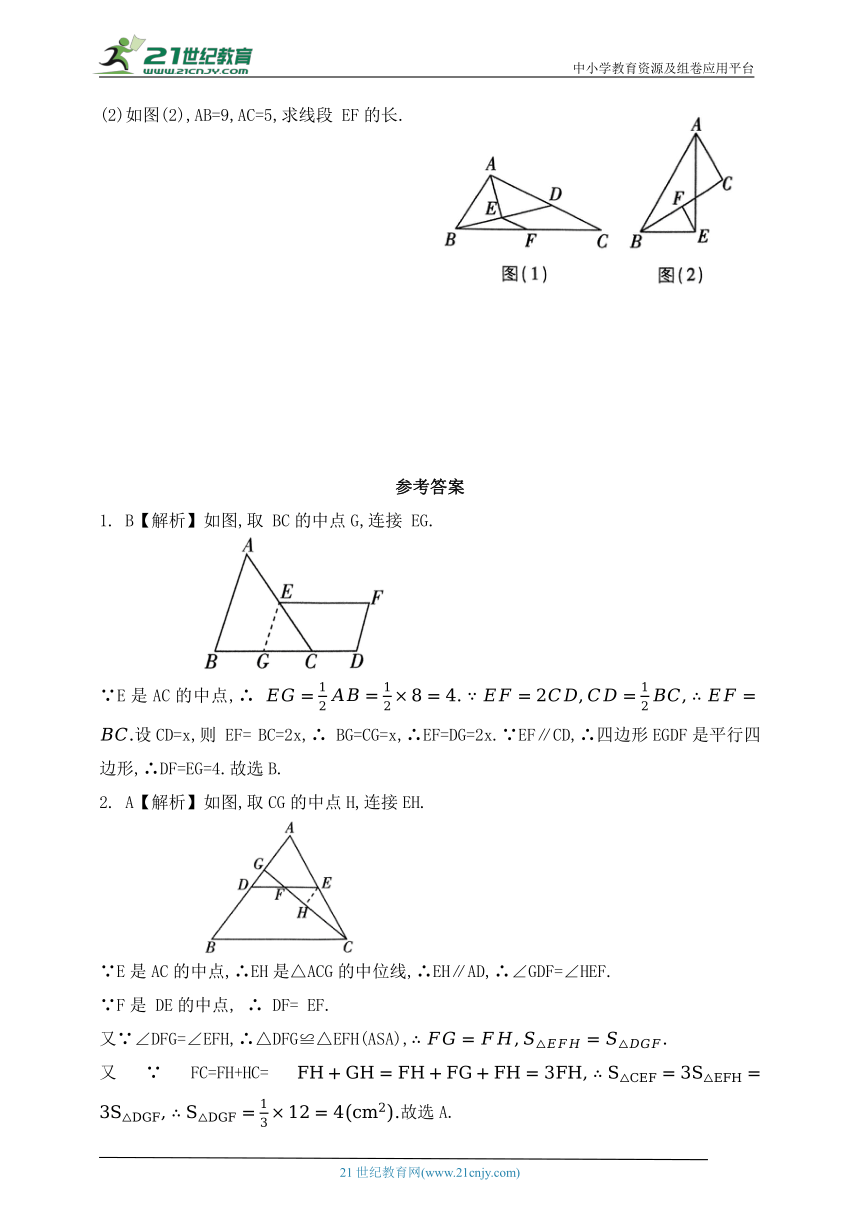
11.如图,在△ABC中,点 M 为 BC的中点,AD为△ABC的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为_____________.
12.如图,在△ABC中,AD 是中线,AE是∠BAC 的平分线,CF⊥AE于 F,AB= 10,AC=6,求 DF 的长.
13.如图,在△ABC中,AE 平分∠BAC,BE⊥AE于点E,点F是BC的中点,连接EF.
(1)如图(1),BE的延长线与AC边相交于点D,求证:
(2)如图(2),AB=9,AC=5,求线段 EF的长.
参考答案
1. B【解析】如图,取 BC的中点G,连接 EG.
∵E是AC的中点,∴ 设CD=x,则 EF= BC=2x,∴ BG=CG=x,∴EF=DG=2x.∵EF∥CD,∴四边形EGDF是平行四边形,∴DF=EG=4.故选B.
2. A【解析】如图,取CG的中点H,连接EH.
∵E是AC的中点,∴EH是△ACG的中位线,∴EH∥AD,∴∠GDF=∠HEF.
∵F是 DE的中点, ∴ DF= EF.
又∵∠DFG=∠EFH,∴△DFG≌△EFH(ASA),
又∵FC=FH+HC=故选A.
3. C【解析】如图,连接BD,取BD的中点G,连接 MG,NG.
∵点 M,N分别是AD,BC的中点,∴MG是△ABD的中位线,NG是△BCD的中位线,∴AB=2MG,DC=2NG.∵AB=4,DC=2,∴MG=2,NG=1,由三角形三边关系得 MG-NG【解析】如图,取CN的中点E,连接DE.
∵AD是△ABC 的中线,∴ BD=CD.∵CE=EN,∴DE∥BN.
∵M是AD的中点,∴易知点N为AE 中点,∴AN= EN,∴AN= EN= CE=
故答案为
第4题图 第5题图
5.【证明】如图,取AB的中点G,连接 MG,NG.
∵M,N分别为AF,BE的中点,∴
CF,AC⊥BC,∴ AE= BF,NG⊥MG,∴ MG=NG,∠MGN=90°,
∴△MNG是等腰直角三角形,∴MG +NG =MN ,∴2NG =MN .
∵AE=2NG,∴AE =4NG =2MN .
6. D【解析】如图,连接 DN.
∵点E,F分别为DM,MN的中点,∴EF是△MND的中位线,
点M,N分别为线段 BC,AB上的动点(含端点,但点M不与点B重合),∴当点N与点B重合时,DN有最大值,此时 ∴EF长度的最大值为 故选D.
7.6【解析】如图,连接EF.
∵E,F分别是 AB,BC的中点,∴EF是△BAC的中位线,∴ F∥AC.
∵EH⊥AC,∴EH⊥EF,即∠FEG=90°,故答案为6.
8.【证明】连接EH,GH,GF.
∵E,F,G,H分别是 BD,BC,AC,AD的中点,∴AB∥EH∥GF,GH∥BC,∴GH∥EF,∴四边形EHGF为平行四边形.∵GE,HF为平行四边形EHGF的对角线,∴EG,HF互相平分.
9.2 【解析】取BE的中点M,连接 FM,CM,如图所示.
∵F为AE的中点,M为BE的中点,∥
四边形 ABCD 是平行四边形,∴ DC=AB,DC∥AB.
∵E为CD的中点 四边形EFMC 是平行四边形,∴EG=GM.
∵BM= 故答案为2.
10.(1)【解】如图,取BD的中点P,连接EP,FP.
∵E,F分别是AD,BC的中点,AB=6,CD=8,∴ PE∥AB,且且 又∵∠ABD=30°,∠BDC=120°,∴∠EPD=∠ABD= 30°,∠DPF= 180°-∠BDC=60°,∴∠EPF=∠EPD+∠DPF=90°.
在 Rt△EPF中,由勾股定理得 EF=
(2)【证明】∵E,F分别是AD,BC的中点,∴PE∥AB,且 PF∥CD,且 ∴∠EPD=∠ABD,∠DPF=180°-∠BDC.
∵∠BDC-∠ABD=90°,∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°-∠BDC=∠ABD+180°-(90°+∠ABD)= 90°,
∴AB +CD =4EF .
11.7.5【解析】如图,延长BD交CA的延长线于E.∵AD为∠BAE的平分线,BD⊥AD,
∴∠EAD=∠BAD,∠ADE=∠ADB= 90°.
∵AD=AD,∴△ADE≌△ADB(ASA),∴BD=DE,AB=AE= 6,∴ CE=AC+AE=9+6= 15.
又∵M为BC的中点,∴DM 是△BCE的中位线,∴ 故答案为7.5.
第11题图 第12题图
12.【解】如图,延长CF 交AB 于点 G,交AD于点H.
∵ AE 平分∠BAC,∴∠GAF=∠CAF.∵AF⊥CG,∴∠AFG=∠AFC=90°.
又∵AF=AF,∴△AFG≌△AFC(ASA),∴AG= AC,GF=CF.
又∵点 D是 BC中点,∴DF是△CBG的中位线,∴
13.(1)【证明】∵AE 平分∠BAC,∴∠BAE=∠DAE.∵BE⊥AE,∴∠AEB=∠AED=90°.
在△AEB和△AED中 ∴△AEB≌△AED(ASA),
∴ BE= ED,AD=
(2)【解】如图,分别延长BE,AC交于点 H.
同(1) 可证明△ABE≌△AHE,∴ BE= EH, AH=AB=9.
∵BE=EH,BF=FC,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
专题 构造中位线的方法
类型1 取一边中点构造三角形的中位线
1.如图,在△ABC中,延长BC至D,使得 过AC 中点 E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
A.3 B.4
第1题图 第2题图
2.如图,DE 是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12 cm ,则 的值为( )
A.4 cm B.6cm C.8cm D.9 cm
3.如图,在四边形 ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2.对于MN的长,给出了四种猜测:①MN=4;②MN=3;③MN=2;④MN=1.猜测正确的是( )
A.① B.② C.③ D.④
第3题图 第4题图
4.如图,AD是△ABC的中线,M是AD的中点,连接BM并延长交AC于点 N,若AC=4,则AN=___________.
5.如图,在△ABC中,∠C=90°,CA= CB,E,F分别为CA,CB上一点,且CE= CF,M,N分别为AF,BE的中点,求证:AE =2MN .
类型2 连接两点构造三角形的中位线
6.如图,四边形 ABCD中,∠A= 90°,AB= 8,AD=6,点 M,N分别为线段 BC,AB上的动点(含端点,但点 M不与点 B重合),点E,F分别为DM,MN的中点,则 EF长度的最大值为( )
A.8 B.7 C.6 D.5
第6题图 第7题图
7.如图,在 ABCD中,E,F分别是AB,BC的中点,EH⊥AC,垂足为H,与AF交于点G,若 则EG的长为____________.
8.已知在△ABC中,D是BC上的一点,E,F,G,H分别是 BD,BC,AC,AD的中点.
求证:EG,HF互相平分.
类型3 取连接线中点构造三角形中位线
9.如图,在 ABCD中,E是CD的中点,连接AE,BE,F是AE的中点,连接CF交BE于点G,若BE= 8,则 GE的长为____________.
10.如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;
(2)若∠BDC-∠ABD=90°,求证:AB +CD =4EF .
类型4 利用角平分线和垂直构造三角形的中位线
11.如图,在△ABC中,点 M 为 BC的中点,AD为△ABC的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为_____________.
12.如图,在△ABC中,AD 是中线,AE是∠BAC 的平分线,CF⊥AE于 F,AB= 10,AC=6,求 DF 的长.
13.如图,在△ABC中,AE 平分∠BAC,BE⊥AE于点E,点F是BC的中点,连接EF.
(1)如图(1),BE的延长线与AC边相交于点D,求证:
(2)如图(2),AB=9,AC=5,求线段 EF的长.
参考答案
1. B【解析】如图,取 BC的中点G,连接 EG.
∵E是AC的中点,∴ 设CD=x,则 EF= BC=2x,∴ BG=CG=x,∴EF=DG=2x.∵EF∥CD,∴四边形EGDF是平行四边形,∴DF=EG=4.故选B.
2. A【解析】如图,取CG的中点H,连接EH.
∵E是AC的中点,∴EH是△ACG的中位线,∴EH∥AD,∴∠GDF=∠HEF.
∵F是 DE的中点, ∴ DF= EF.
又∵∠DFG=∠EFH,∴△DFG≌△EFH(ASA),
又∵FC=FH+HC=故选A.
3. C【解析】如图,连接BD,取BD的中点G,连接 MG,NG.
∵点 M,N分别是AD,BC的中点,∴MG是△ABD的中位线,NG是△BCD的中位线,∴AB=2MG,DC=2NG.∵AB=4,DC=2,∴MG=2,NG=1,由三角形三边关系得 MG-NG
∵AD是△ABC 的中线,∴ BD=CD.∵CE=EN,∴DE∥BN.
∵M是AD的中点,∴易知点N为AE 中点,∴AN= EN,∴AN= EN= CE=
故答案为
第4题图 第5题图
5.【证明】如图,取AB的中点G,连接 MG,NG.
∵M,N分别为AF,BE的中点,∴
CF,AC⊥BC,∴ AE= BF,NG⊥MG,∴ MG=NG,∠MGN=90°,
∴△MNG是等腰直角三角形,∴MG +NG =MN ,∴2NG =MN .
∵AE=2NG,∴AE =4NG =2MN .
6. D【解析】如图,连接 DN.
∵点E,F分别为DM,MN的中点,∴EF是△MND的中位线,
点M,N分别为线段 BC,AB上的动点(含端点,但点M不与点B重合),∴当点N与点B重合时,DN有最大值,此时 ∴EF长度的最大值为 故选D.
7.6【解析】如图,连接EF.
∵E,F分别是 AB,BC的中点,∴EF是△BAC的中位线,∴ F∥AC.
∵EH⊥AC,∴EH⊥EF,即∠FEG=90°,故答案为6.
8.【证明】连接EH,GH,GF.
∵E,F,G,H分别是 BD,BC,AC,AD的中点,∴AB∥EH∥GF,GH∥BC,∴GH∥EF,∴四边形EHGF为平行四边形.∵GE,HF为平行四边形EHGF的对角线,∴EG,HF互相平分.
9.2 【解析】取BE的中点M,连接 FM,CM,如图所示.
∵F为AE的中点,M为BE的中点,∥
四边形 ABCD 是平行四边形,∴ DC=AB,DC∥AB.
∵E为CD的中点 四边形EFMC 是平行四边形,∴EG=GM.
∵BM= 故答案为2.
10.(1)【解】如图,取BD的中点P,连接EP,FP.
∵E,F分别是AD,BC的中点,AB=6,CD=8,∴ PE∥AB,且且 又∵∠ABD=30°,∠BDC=120°,∴∠EPD=∠ABD= 30°,∠DPF= 180°-∠BDC=60°,∴∠EPF=∠EPD+∠DPF=90°.
在 Rt△EPF中,由勾股定理得 EF=
(2)【证明】∵E,F分别是AD,BC的中点,∴PE∥AB,且 PF∥CD,且 ∴∠EPD=∠ABD,∠DPF=180°-∠BDC.
∵∠BDC-∠ABD=90°,∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°-∠BDC=∠ABD+180°-(90°+∠ABD)= 90°,
∴AB +CD =4EF .
11.7.5【解析】如图,延长BD交CA的延长线于E.∵AD为∠BAE的平分线,BD⊥AD,
∴∠EAD=∠BAD,∠ADE=∠ADB= 90°.
∵AD=AD,∴△ADE≌△ADB(ASA),∴BD=DE,AB=AE= 6,∴ CE=AC+AE=9+6= 15.
又∵M为BC的中点,∴DM 是△BCE的中位线,∴ 故答案为7.5.
第11题图 第12题图
12.【解】如图,延长CF 交AB 于点 G,交AD于点H.
∵ AE 平分∠BAC,∴∠GAF=∠CAF.∵AF⊥CG,∴∠AFG=∠AFC=90°.
又∵AF=AF,∴△AFG≌△AFC(ASA),∴AG= AC,GF=CF.
又∵点 D是 BC中点,∴DF是△CBG的中位线,∴
13.(1)【证明】∵AE 平分∠BAC,∴∠BAE=∠DAE.∵BE⊥AE,∴∠AEB=∠AED=90°.
在△AEB和△AED中 ∴△AEB≌△AED(ASA),
∴ BE= ED,AD=
(2)【解】如图,分别延长BE,AC交于点 H.
同(1) 可证明△ABE≌△AHE,∴ BE= EH, AH=AB=9.
∵BE=EH,BF=FC,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
