5.4多边形的内角和与外角和 第1课时 多边形的内角和(含答案)
文档属性
| 名称 | 5.4多边形的内角和与外角和 第1课时 多边形的内角和(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
4 多边形的内角和与外角和
第1课时 多边形的内角和
刷基础
知识点1 多边形与三角形的关系
1.过多边形一个顶点的所有对角线把这个多边形分成了7个三角形,则这个多边形的边数是( )
A.8 B.9 C. 10 D.11
2.过m边形的一个顶点能作7条对角线,n边形没有对角线,k边形有k条对角线,则
知识点2 与多边形内角和有关的计算
3.一个多边形的内角和为1800°,则这个多边形的边数为( )
A.9 B. 10 C. 11 D.12
4.如图,若∠1+∠2+∠3+∠4=278°,则∠5+∠6+∠7+∠8=_____________.
5.若将一个多边形剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是___________.
6.如图,求∠A,∠B,∠C,∠D,∠E,∠F,∠G的度数和.
知识点3 与正多边形有关的计算
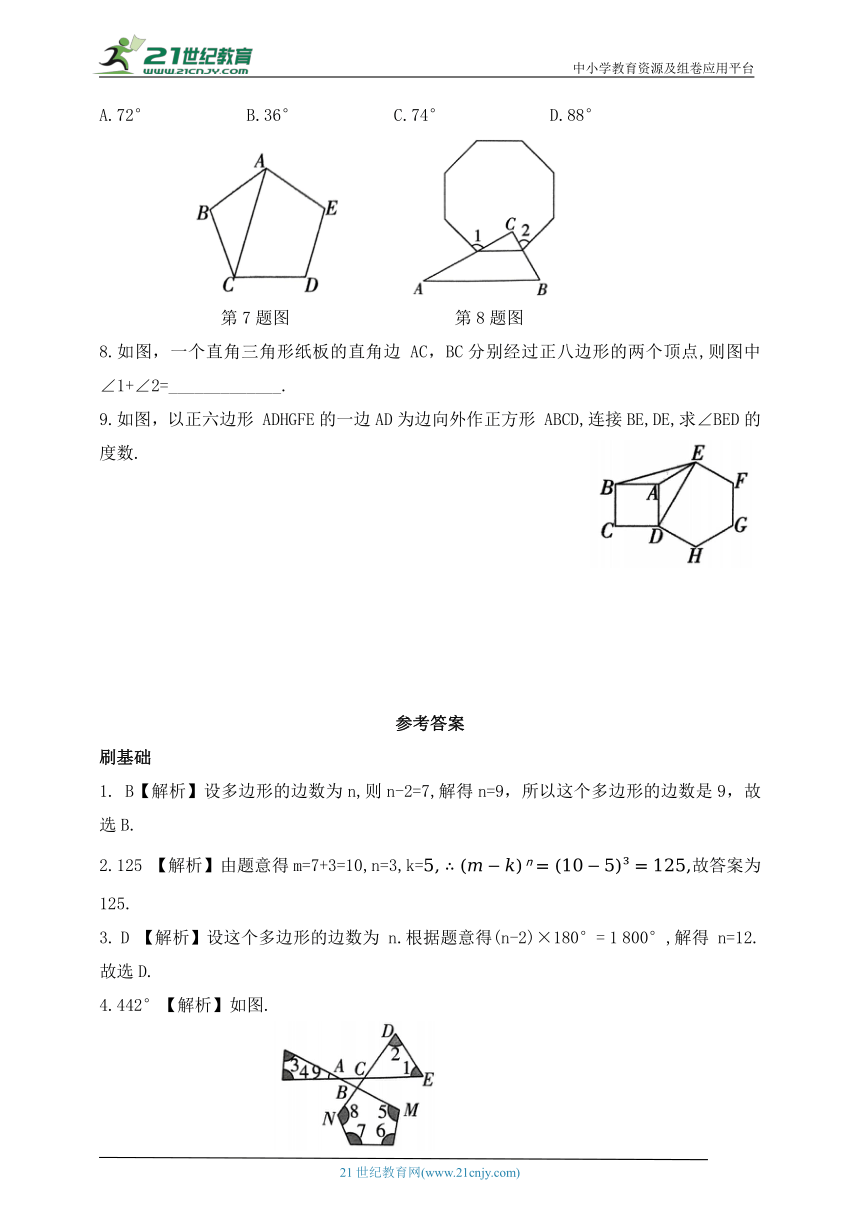
7.如图,AC是正五边形ABCDE的对角线,∠ACD的度数是 ( )
A.72° B.36° C.74° D.88°
第7题图 第8题图
8.如图,一个直角三角形纸板的直角边 AC,BC分别经过正八边形的两个顶点,则图中 ∠1+∠2=_____________.
9.如图,以正六边形 ADHGFE的一边AD为边向外作正方形 ABCD,连接BE,DE,求∠BED的度数.
参考答案
刷基础
1. B【解析】设多边形的边数为n,则n-2=7,解得n=9,所以这个多边形的边数是9,故选B.
2.125 【解析】由题意得m=7+3=10,n=3,k=故答案为125.
3. D 【解析】设这个多边形的边数为 n.根据题意得(n-2)×180°= 1 800°,解得 n=12.故选D.
4.442°【解析】如图.
∵∠1+∠2+∠3+∠4 =278°,∴ ∠9 +∠DCE =180°+ 180°-278°= 82°,
∴∠CAB+∠ACB=∠9+∠DCE=82°,∴∠NBM=∠ABC=180°-82°=98°,
∴∠5+∠6+∠7+∠8=(5-2)×180°-98°=442°.故答案为442°.
5.5或6或7【解析】设内角和为720°的多边形的边数是n,则(n-2)·180°= 720°,解得
n=6.∵将原多边形剪去一个角后边数不变或减少1或增加1,∴原多边形的边数为5或6
或7.
6.【解】连接 FC.∵∠D+∠E+∠DIE=∠ICF+∠IFC+∠FIC=180°,∠DIE=∠FIC,
∴∠D+∠E=∠ICF+∠IFC.∵∠A+∠B+∠BCF+∠CFG+∠G=540°,
∴∠A+∠B+∠BCD+∠D+∠E+∠EFG+∠G=540°.
7. A【解析】∵五边形 ABCDE是正五边形,
∴∠B=∠BCD= 108°,AB= BC,∴∠BCA=∠BAC= 36°,∴∠ACD= 108°-36°=72°.
故选A.
8.180°【解析】如图.∵∠C=90°,∴∠3+∠4=90°.∵正八边形的每个内角的度数为∠2=135°×2-90°=180°.故答案为180°.
9.【解】∵六边形 ADHGFE为正六边形,∴AE=AD,∠DAE=120°,
∵四边形ABCD为正方形,∴AB=AD=AE,∠BAD=90°,
∴∠BAE=360°-120°-90°= 150°,
∴∠BED=∠AEB+∠AED=15°+30°=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
4 多边形的内角和与外角和
第1课时 多边形的内角和
刷基础
知识点1 多边形与三角形的关系
1.过多边形一个顶点的所有对角线把这个多边形分成了7个三角形,则这个多边形的边数是( )
A.8 B.9 C. 10 D.11
2.过m边形的一个顶点能作7条对角线,n边形没有对角线,k边形有k条对角线,则
知识点2 与多边形内角和有关的计算
3.一个多边形的内角和为1800°,则这个多边形的边数为( )
A.9 B. 10 C. 11 D.12
4.如图,若∠1+∠2+∠3+∠4=278°,则∠5+∠6+∠7+∠8=_____________.
5.若将一个多边形剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是___________.
6.如图,求∠A,∠B,∠C,∠D,∠E,∠F,∠G的度数和.
知识点3 与正多边形有关的计算
7.如图,AC是正五边形ABCDE的对角线,∠ACD的度数是 ( )
A.72° B.36° C.74° D.88°
第7题图 第8题图
8.如图,一个直角三角形纸板的直角边 AC,BC分别经过正八边形的两个顶点,则图中 ∠1+∠2=_____________.
9.如图,以正六边形 ADHGFE的一边AD为边向外作正方形 ABCD,连接BE,DE,求∠BED的度数.
参考答案
刷基础
1. B【解析】设多边形的边数为n,则n-2=7,解得n=9,所以这个多边形的边数是9,故选B.
2.125 【解析】由题意得m=7+3=10,n=3,k=故答案为125.
3. D 【解析】设这个多边形的边数为 n.根据题意得(n-2)×180°= 1 800°,解得 n=12.故选D.
4.442°【解析】如图.
∵∠1+∠2+∠3+∠4 =278°,∴ ∠9 +∠DCE =180°+ 180°-278°= 82°,
∴∠CAB+∠ACB=∠9+∠DCE=82°,∴∠NBM=∠ABC=180°-82°=98°,
∴∠5+∠6+∠7+∠8=(5-2)×180°-98°=442°.故答案为442°.
5.5或6或7【解析】设内角和为720°的多边形的边数是n,则(n-2)·180°= 720°,解得
n=6.∵将原多边形剪去一个角后边数不变或减少1或增加1,∴原多边形的边数为5或6
或7.
6.【解】连接 FC.∵∠D+∠E+∠DIE=∠ICF+∠IFC+∠FIC=180°,∠DIE=∠FIC,
∴∠D+∠E=∠ICF+∠IFC.∵∠A+∠B+∠BCF+∠CFG+∠G=540°,
∴∠A+∠B+∠BCD+∠D+∠E+∠EFG+∠G=540°.
7. A【解析】∵五边形 ABCDE是正五边形,
∴∠B=∠BCD= 108°,AB= BC,∴∠BCA=∠BAC= 36°,∴∠ACD= 108°-36°=72°.
故选A.
8.180°【解析】如图.∵∠C=90°,∴∠3+∠4=90°.∵正八边形的每个内角的度数为∠2=135°×2-90°=180°.故答案为180°.
9.【解】∵六边形 ADHGFE为正六边形,∴AE=AD,∠DAE=120°,
∵四边形ABCD为正方形,∴AB=AD=AE,∠BAD=90°,
∴∠BAE=360°-120°-90°= 150°,
∴∠BED=∠AEB+∠AED=15°+30°=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
