第五章 平行四边形 章末复习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
章末复习
考点1 平行四边形的性质与判定
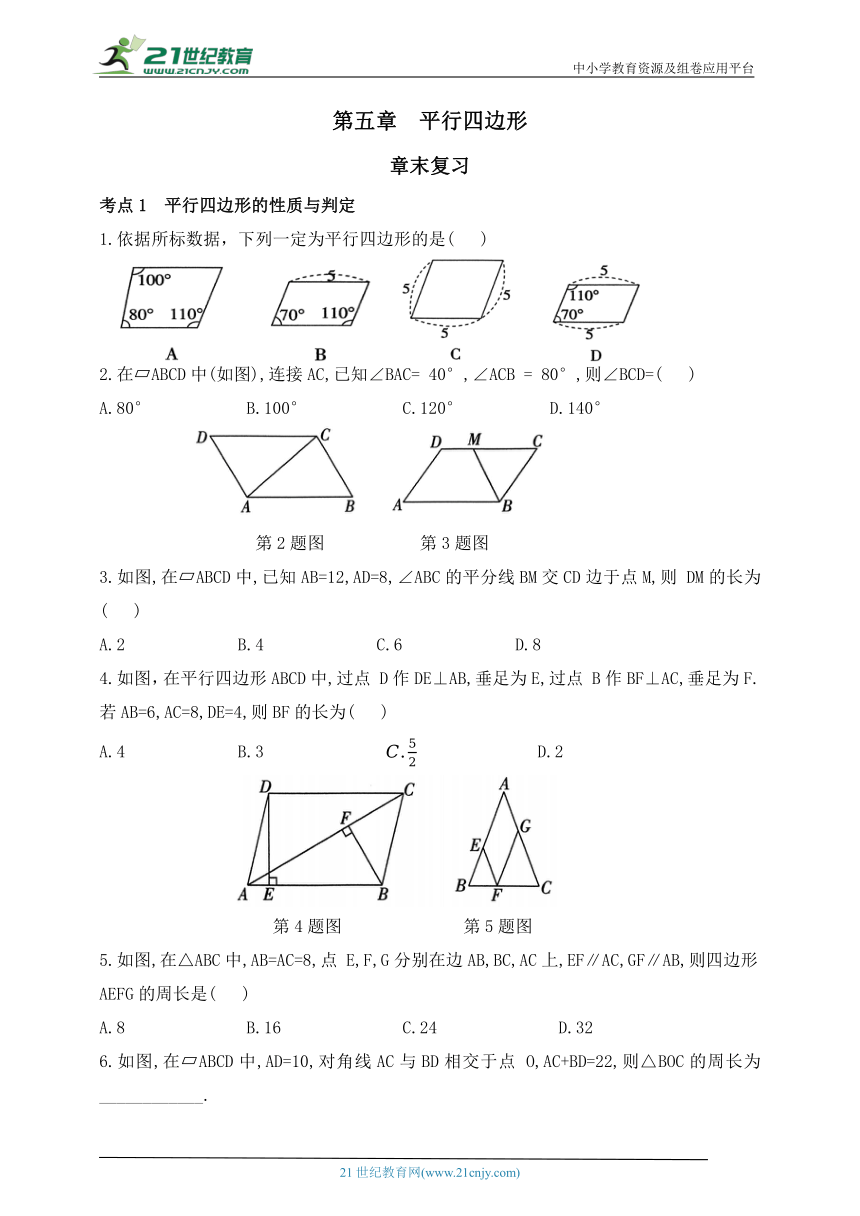
1.依据所标数据,下列一定为平行四边形的是( )
2.在 ABCD中(如图),连接AC,已知∠BAC= 40°,∠ACB = 80°,则∠BCD=( )
A.80° B.100° C.120° D.140°
第2题图 第3题图
3.如图,在 ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则 DM的长为( )
A.2 B.4 C.6 D.8
4.如图,在平行四边形ABCD中,过点 D作DE⊥AB,垂足为E,过点 B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3 D.2
第4题图 第5题图
5.如图,在△ABC中,AB=AC=8,点 E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( )
A.8 B.16 C.24 D.32
6.如图,在 ABCD中,AD=10,对角线AC与BD相交于点 O,AC+BD=22,则△BOC的周长为____________.
第6题图 第7题图
7.如图,四边形ABCD为平行四边形,则点B的坐标为____________.
8.如图,在 ABCD中,DF平分∠ADC,交AB于点 F,BE∥DF,交AD的延长线于点 E.若 ∠A=40°,求∠ABE的度数.
9.如图,在 ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
考点2 三角形中位线定理
10.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形 BDEF的周长是( )
A.28 B.14 C.10 D.7
第10题图 第11题图
11.如图,在四边形ABCD中,点E,F,G,H分别是 AB,BC,CD,DA边上的中点,则下列结论一定正确的是( )
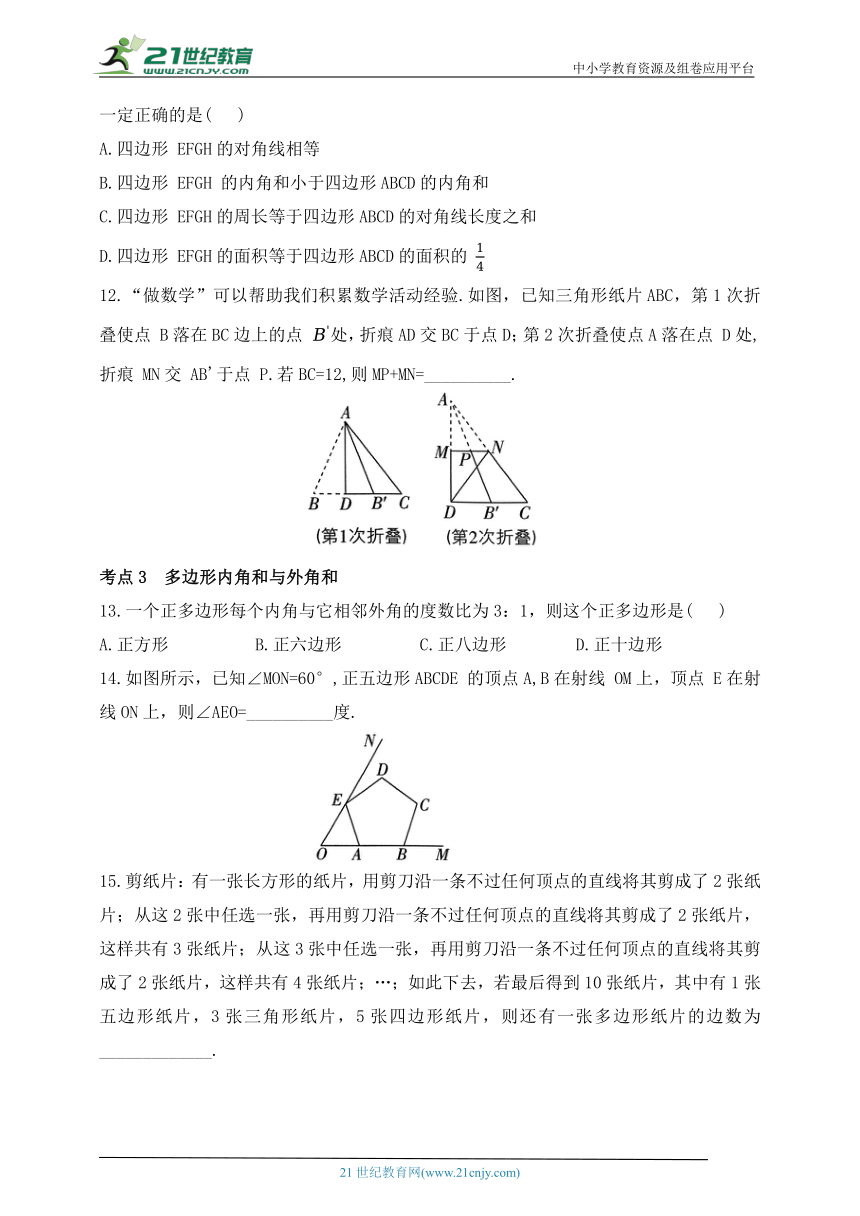
A.四边形 EFGH的对角线相等
B.四边形 EFGH 的内角和小于四边形ABCD的内角和
C.四边形 EFGH的周长等于四边形ABCD的对角线长度之和
D.四边形 EFGH的面积等于四边形ABCD的面积的
12.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC,第1次折叠使点 B落在BC边上的点 处,折痕AD交BC于点D;第2次折叠使点A落在点 D处,折痕 MN交 AB'于点 P.若BC=12,则MP+MN=__________.
考点3 多边形内角和与外角和
13.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )
A.正方形 B.正六边形 C.正八边形 D.正十边形
14.如图所示,已知∠MON=60°,正五边形ABCDE 的顶点A,B在射线 OM上,顶点 E在射线ON上,则∠AEO=__________度.
15.剪纸片:有一张长方形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片;从这3张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有4张纸片;…;如此下去,若最后得到10张纸片,其中有1张五边形纸片,3张三角形纸片,5张四边形纸片,则还有一张多边形纸片的边数为_____________.
参考答案
1. D【解析】A选项,只有一组对边平行的四边形不能确定是平行四边形,故A选项不符合题意;B选项,只有一组对边平行的四边形不能确定是平行四边形,故B 选项不符合题意;C选项,只有一组对边相等的四边形不能确定是平行四边形,故C选项不符合题意;D选项,有一组对边平行且相等的四边形是平行四边形,故D选项符合题意.故选D.
2. C 【解析】∵四边形ABCD 是平行四边形,
∴AB∥CD.∵∠BAC=40°,∴∠ACD=∠BAC=40°.
∵∠ACB=80°,∴∠BCD=∠ACB+∠ACD=120°,故选C.
3. B【解析】∵四边形 ABCD是平行四边形,∴CD= AB = 12,BC = AD= 8,AB∥CD,
∴∠ABM=∠CMB.∵BM是∠ABC的平分线,∴∠ABM=∠CBM,∴∠CBM=∠CMB,
∴MC=BC=8,∴DM=CD-MC=12-8=4,故选B.
4. B【解析】在平行四边形ABCD中, 平行四边形ABCD ,
∴8BF=6×4,解得BF=3.故选B.
5. B【解析】∵EF∥AC,GF∥AB,∴ 四边形AEFG是平行四边形,∠B=∠GFC,∠C=∠EFB.∵AB= AC,∴∠B=∠C,∴∠B=∠EFB,∠GFC=∠C,∴ EB = EF,FG= GC,
∴四边形AEFG的周长为AE+EF+FG+AG=AE+EB+GC+AG= AB+AC.
∵AB=AC= 8,∴四边形AEFG的周长为AB+AC=8+8= 16,故选B.
6.21 【解析】∵四边形ABCD是平行四边形,的周长为OC+OB+BC=11+10=21.
7.(-2,-1) 【解析】∵四边形ABCD为平行四边形,且A(-1,2),D(3,2),∴AD∥BC∥x轴,
AD=BC=4.∵C(2,-1),∴B(-2,-1).故答案为(-2,-1).
8.【解】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A+∠ADC=180°.
∵∠A=40°,∴∠ADC=140°.∵DF平分∠ADC,
∴∠AFD=∠CDF=70°.∵DF∥BE,∴∠ABE=∠AFD=70°.
9.【证明】(1)∵四边形 ABCD为平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB.
在△ABE和△CDF中, ∴△ABE≌△CDF(SAS).
(2)由(1)可知,△ABE≌△CDF,∴ AE=CF,∠AEB=∠CFD,∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE,∴AE∥CF.∵AE=CF,AE∥CF,∴四边形AECF是平行四边形.
10. B【解析】∵D,E,F分别是BC,AC,AB的中点,. 4,∴四边形BDEF的周长为2×(3+4)= 14,故选B.
11. C【解析】如图,连接AC,BD. A选项,在四边形ABCD 中,∵点E,F,G,H分别是AB,BC,CD,DA 边上的中点,∴ EH∥BD,EH=FG,∴四边形 EFGH是平行四边形,无法进一步证得 EFGH的对角线相等,故A选项错误;B选项,∵四边形EFGH的内角和等于360°,四边形ABCD的内角和等于360°,故B选项错误;C 选项,∵ 点E,F,G,H分别是AB,BC,CD,DA边上的中点,∴ 同理可得EF+HG=AC,∴四边形EFGH的周长等于四边形ABCD的对角线长度之和,故C选项正确;D选项,四边形 EFGH的面积等于四边形ABCD的面积的 故D选项错误.故选C.
12.6【解析】如图,补上AB,BD,延长NM交AB于G.
由折叠得AM=MD,MN⊥AD,AD⊥BC,∴GN∥BC,∴易得AG=BG,AN= NC,
∴ GN是△ABC的中位线, 6.
∵PM=GM,∴MP+MN=GM+MN=GN=6.
13. C【解析】∵一个正多边形每个内角与它相邻外角的度数比为3:1,∴设这个外角是
x°,则内角是3x°.根据题意得x+3x=180,解得x=45.∵360°÷45°=8,∴这个正多边形是正八边形.故选C.
14.48【解析】∵五边形ABCDE 是正五边形,
是△AEO的外角,∴∠AEO=∠EAB-∠MON=108°-60°=48°.
15.6【解析】根据题意,用剪刀沿一条不过任何顶点的直线将1张纸片剪成了2张纸片,
则每剪一次,所有的多边形的内角和增加360°,最后得到10张纸片,则剪了9次.∵有
1张五边形纸片,3张三角形纸片,5张四边形纸片,设还有一张多边形纸片的边数为n,
∴(5-2)×180°+3×180°+(4-2)×180°×5+(n-2)×180°=360°+360°×9,解得 n=6.故
答案为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
章末复习
考点1 平行四边形的性质与判定
1.依据所标数据,下列一定为平行四边形的是( )
2.在 ABCD中(如图),连接AC,已知∠BAC= 40°,∠ACB = 80°,则∠BCD=( )
A.80° B.100° C.120° D.140°
第2题图 第3题图
3.如图,在 ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则 DM的长为( )
A.2 B.4 C.6 D.8
4.如图,在平行四边形ABCD中,过点 D作DE⊥AB,垂足为E,过点 B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3 D.2
第4题图 第5题图
5.如图,在△ABC中,AB=AC=8,点 E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( )
A.8 B.16 C.24 D.32
6.如图,在 ABCD中,AD=10,对角线AC与BD相交于点 O,AC+BD=22,则△BOC的周长为____________.
第6题图 第7题图
7.如图,四边形ABCD为平行四边形,则点B的坐标为____________.
8.如图,在 ABCD中,DF平分∠ADC,交AB于点 F,BE∥DF,交AD的延长线于点 E.若 ∠A=40°,求∠ABE的度数.
9.如图,在 ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
考点2 三角形中位线定理
10.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形 BDEF的周长是( )
A.28 B.14 C.10 D.7
第10题图 第11题图
11.如图,在四边形ABCD中,点E,F,G,H分别是 AB,BC,CD,DA边上的中点,则下列结论一定正确的是( )
A.四边形 EFGH的对角线相等
B.四边形 EFGH 的内角和小于四边形ABCD的内角和
C.四边形 EFGH的周长等于四边形ABCD的对角线长度之和
D.四边形 EFGH的面积等于四边形ABCD的面积的
12.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC,第1次折叠使点 B落在BC边上的点 处,折痕AD交BC于点D;第2次折叠使点A落在点 D处,折痕 MN交 AB'于点 P.若BC=12,则MP+MN=__________.
考点3 多边形内角和与外角和
13.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )
A.正方形 B.正六边形 C.正八边形 D.正十边形
14.如图所示,已知∠MON=60°,正五边形ABCDE 的顶点A,B在射线 OM上,顶点 E在射线ON上,则∠AEO=__________度.
15.剪纸片:有一张长方形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片;从这3张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有4张纸片;…;如此下去,若最后得到10张纸片,其中有1张五边形纸片,3张三角形纸片,5张四边形纸片,则还有一张多边形纸片的边数为_____________.
参考答案
1. D【解析】A选项,只有一组对边平行的四边形不能确定是平行四边形,故A选项不符合题意;B选项,只有一组对边平行的四边形不能确定是平行四边形,故B 选项不符合题意;C选项,只有一组对边相等的四边形不能确定是平行四边形,故C选项不符合题意;D选项,有一组对边平行且相等的四边形是平行四边形,故D选项符合题意.故选D.
2. C 【解析】∵四边形ABCD 是平行四边形,
∴AB∥CD.∵∠BAC=40°,∴∠ACD=∠BAC=40°.
∵∠ACB=80°,∴∠BCD=∠ACB+∠ACD=120°,故选C.
3. B【解析】∵四边形 ABCD是平行四边形,∴CD= AB = 12,BC = AD= 8,AB∥CD,
∴∠ABM=∠CMB.∵BM是∠ABC的平分线,∴∠ABM=∠CBM,∴∠CBM=∠CMB,
∴MC=BC=8,∴DM=CD-MC=12-8=4,故选B.
4. B【解析】在平行四边形ABCD中, 平行四边形ABCD ,
∴8BF=6×4,解得BF=3.故选B.
5. B【解析】∵EF∥AC,GF∥AB,∴ 四边形AEFG是平行四边形,∠B=∠GFC,∠C=∠EFB.∵AB= AC,∴∠B=∠C,∴∠B=∠EFB,∠GFC=∠C,∴ EB = EF,FG= GC,
∴四边形AEFG的周长为AE+EF+FG+AG=AE+EB+GC+AG= AB+AC.
∵AB=AC= 8,∴四边形AEFG的周长为AB+AC=8+8= 16,故选B.
6.21 【解析】∵四边形ABCD是平行四边形,的周长为OC+OB+BC=11+10=21.
7.(-2,-1) 【解析】∵四边形ABCD为平行四边形,且A(-1,2),D(3,2),∴AD∥BC∥x轴,
AD=BC=4.∵C(2,-1),∴B(-2,-1).故答案为(-2,-1).
8.【解】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A+∠ADC=180°.
∵∠A=40°,∴∠ADC=140°.∵DF平分∠ADC,
∴∠AFD=∠CDF=70°.∵DF∥BE,∴∠ABE=∠AFD=70°.
9.【证明】(1)∵四边形 ABCD为平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB.
在△ABE和△CDF中, ∴△ABE≌△CDF(SAS).
(2)由(1)可知,△ABE≌△CDF,∴ AE=CF,∠AEB=∠CFD,∴180°-∠AEB=180°-∠CFD,
即∠AEF=∠CFE,∴AE∥CF.∵AE=CF,AE∥CF,∴四边形AECF是平行四边形.
10. B【解析】∵D,E,F分别是BC,AC,AB的中点,. 4,∴四边形BDEF的周长为2×(3+4)= 14,故选B.
11. C【解析】如图,连接AC,BD. A选项,在四边形ABCD 中,∵点E,F,G,H分别是AB,BC,CD,DA 边上的中点,∴ EH∥BD,EH=FG,∴四边形 EFGH是平行四边形,无法进一步证得 EFGH的对角线相等,故A选项错误;B选项,∵四边形EFGH的内角和等于360°,四边形ABCD的内角和等于360°,故B选项错误;C 选项,∵ 点E,F,G,H分别是AB,BC,CD,DA边上的中点,∴ 同理可得EF+HG=AC,∴四边形EFGH的周长等于四边形ABCD的对角线长度之和,故C选项正确;D选项,四边形 EFGH的面积等于四边形ABCD的面积的 故D选项错误.故选C.
12.6【解析】如图,补上AB,BD,延长NM交AB于G.
由折叠得AM=MD,MN⊥AD,AD⊥BC,∴GN∥BC,∴易得AG=BG,AN= NC,
∴ GN是△ABC的中位线, 6.
∵PM=GM,∴MP+MN=GM+MN=GN=6.
13. C【解析】∵一个正多边形每个内角与它相邻外角的度数比为3:1,∴设这个外角是
x°,则内角是3x°.根据题意得x+3x=180,解得x=45.∵360°÷45°=8,∴这个正多边形是正八边形.故选C.
14.48【解析】∵五边形ABCDE 是正五边形,
是△AEO的外角,∴∠AEO=∠EAB-∠MON=108°-60°=48°.
15.6【解析】根据题意,用剪刀沿一条不过任何顶点的直线将1张纸片剪成了2张纸片,
则每剪一次,所有的多边形的内角和增加360°,最后得到10张纸片,则剪了9次.∵有
1张五边形纸片,3张三角形纸片,5张四边形纸片,设还有一张多边形纸片的边数为n,
∴(5-2)×180°+3×180°+(4-2)×180°×5+(n-2)×180°=360°+360°×9,解得 n=6.故
答案为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
