第五章 平行四边形 综合测试卷(含答案)
文档属性
| 名称 | 第五章 平行四边形 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 08:22:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
综合测试卷
一、选择题(每小题3分,共30分)
1.若正多边形的一个外角是45°,则该正多边形的内角和为( )
A.540° B.720° C.900° D.1080°
2.如图,在平行四边形ABCD中,AE=2,AD=5,∠BCD的平分线交BA的延长线于点 E,则 CD的长为( )
A.3 B.2.5 C.2 D.1.5
3.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
4.如图,E是 ABCD的边AD延长线上一点,连接BE交CD于点F,连接CE,BD,添加以下条件,不能判定四边形BCED为平行四边形的是( )
A. EF=BF B.∠AEB=∠BCD C.∠ABD=∠DCE D.∠AEC=∠CBD
第4题图 第5题图
5.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包括△ABD)有( )
A.1个 B.2个 C.3个 D.4个
6.如图,∠F=90°,∠A+∠B+∠C+∠D+∠E的度数为( )
A.90°
B.180°
C.270°
D.360°
7.如图,△ABC 是等腰三角形,且AB=AC,点D是底边 BC 上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一种说法是错误的( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一组对边平行的四边形是平行四边形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
8已知:点 D,E分别是△ABC的边 AB,AC的中点,如图所示.
求证:DE∥BC,且
证明:如图,延长DE 到点 F,使EF=DE,连接FC,DC,AF,AE=EC,则四边形ADCF是平行四边形,以下是排序错误的证明过程:①∴DF⊥BC;②∴CF⊥AD,即CF⊥BD;③∴四边形 DBCF是平行四边形;④∴DE∥BC,且 则正确的证明顺序应是()
A.②→③→①→④ B.②→①→③→④ C.①→③→④→② D.①→③→②→④
第8题图 第9题图
9.如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( )
A.55° B.65° C.75° D.85°
10.如图,平行四边形ABCD中,对角线 AC,BD相交于O,BD=2AD,E,F,G 分别是OC,OD,AB的中点,以下结论:①BE⊥AC;②EG=GF;③△EFG≌△GBE;④EA平分∠GEF,其中正确的是( )
A.①②③ B.①③④ C.①②④ D.②③④
二、填空题(每小题3分,共21分)
11.一个多边形外角和是内角和的 则这个多边形的边数为___________.
12.在平面直角坐标系xOy中,平行四边形OABC的三个顶点O(0,0),A(3,0),B(4,2),则其第四个顶点是___________.
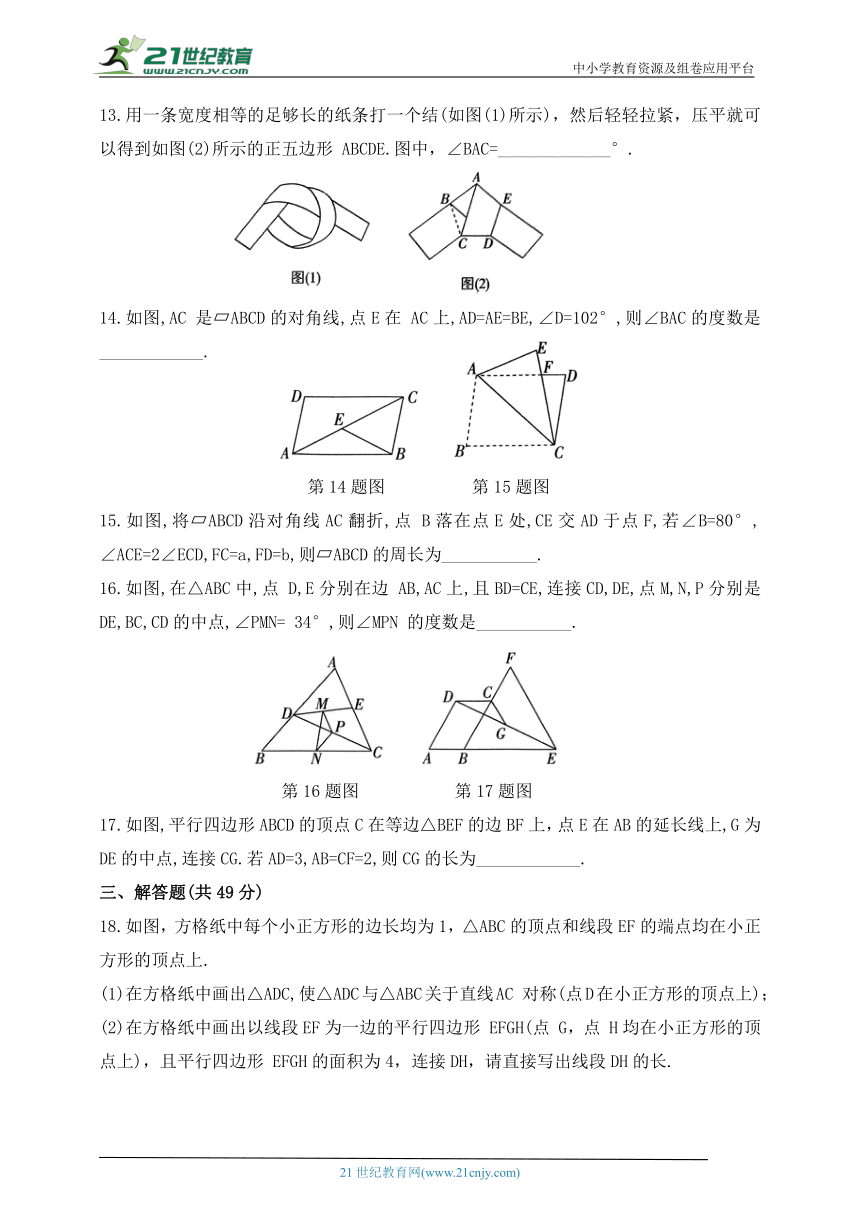
13.用一条宽度相等的足够长的纸条打一个结(如图(1)所示),然后轻轻拉紧,压平就可以得到如图(2)所示的正五边形 ABCDE.图中,∠BAC=_____________°.
14.如图,AC 是 ABCD的对角线,点E在 AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是____________.
第14题图 第15题图
15.如图,将 ABCD沿对角线AC翻折,点 B落在点E处,CE交AD于点F,若∠B=80°, ∠ACE=2∠ECD,FC=a,FD=b,则 ABCD的周长为___________.
16.如图,在△ABC中,点 D,E分别在边 AB,AC上,且BD=CE,连接CD,DE,点M,N,P分别是DE,BC,CD的中点,∠PMN= 34°,则∠MPN 的度数是___________.
第16题图 第17题图
17.如图,平行四边形ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为____________.
三、解答题(共49分)
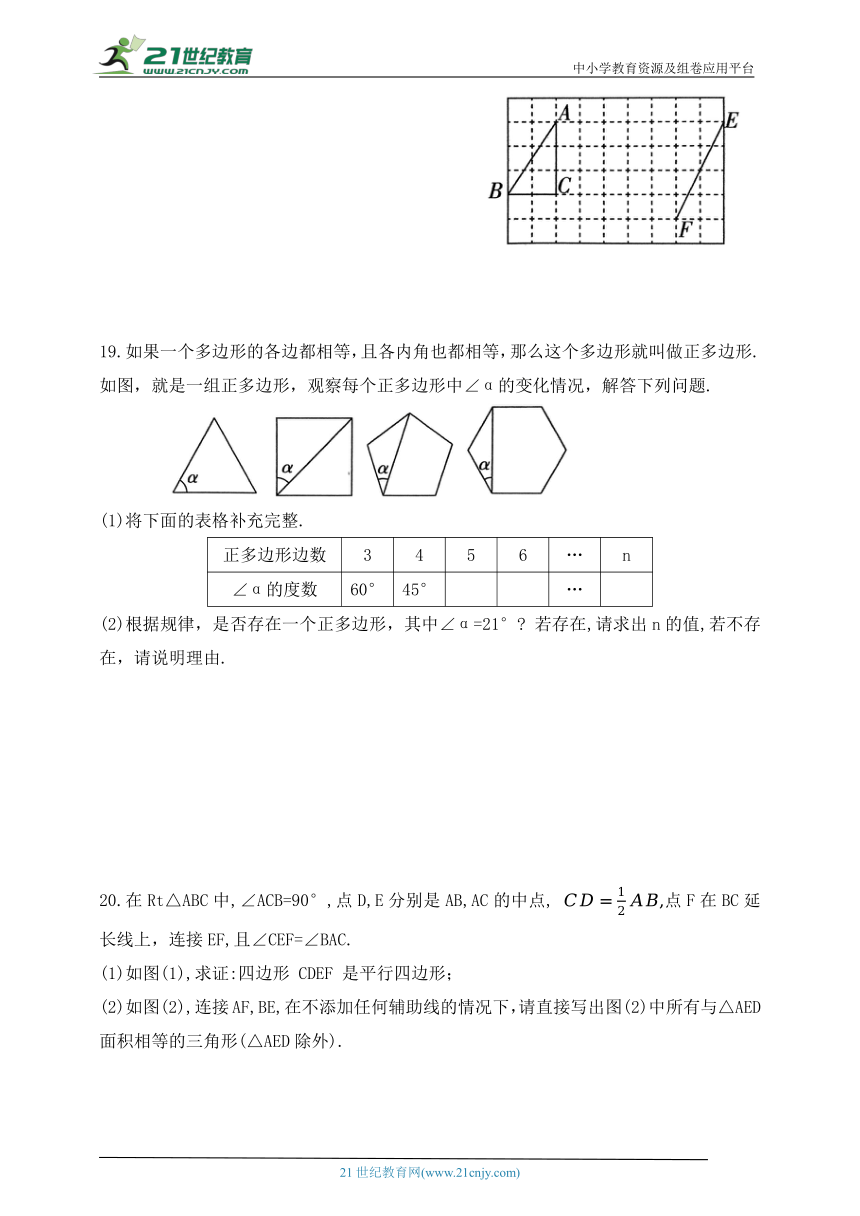
18.如图,方格纸中每个小正方形的边长均为1,△ABC的顶点和线段EF的端点均在小正方形的顶点上.
(1)在方格纸中画出△ADC,使△ADC与△ABC关于直线AC 对称(点D在小正方形的顶点上);
(2)在方格纸中画出以线段EF为一边的平行四边形 EFGH(点 G,点 H均在小正方形的顶点上),且平行四边形 EFGH的面积为4,连接DH,请直接写出线段DH的长.
19.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.
(1)将下面的表格补充完整.
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° …
(2)根据规律,是否存在一个正多边形,其中∠α=21° 若存在,请求出n的值,若不存在,请说明理由.
20.在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点, 点F在BC延长线上,连接EF,且∠CEF=∠BAC.
(1)如图(1),求证:四边形 CDEF 是平行四边形;
(2)如图(2),连接AF,BE,在不添加任何辅助线的情况下,请直接写出图(2)中所有与△AED面积相等的三角形(△AED除外).
21.如图,在平行四边形 ABCD中,O 是对角线BD的中点,过点O的直线EF分别交DA,BC的延长线于E,F,连接CO.
(1)求证:AE=CF;
(2)若AE=BC,试探究线段OC 与线段DF之间的关系,并说明理由.
22.如图,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且 m,n满足
(1)求 的值;
(2)D为OA延长线上一动点,以 BD为直角边作等腰直角三角形BDE,过E,A作直线,求直线EA与y轴交点F的坐标;
(3)在(2)的条件下,当AD=4时,在平面内是否存在一点 P,使以B,E,F,P为顶点的四边
形是平行四边形 如果存在,直接写出点P的坐标;若不存在,说明理由.
参考答案
1. D【解析】由题可知,正多边形的边数为360°÷45°=8,∴这个多边形是正八边形,∴该
多边形的内角和为(8-2)×180°=1 080°.故选D.
2. A【解析】∵四边形 ABCD是平行四边形,∴AB∥CD,AD= BC= 5,CD= AB,∴∠E=∠ECD.∵CE 平分∠BCD,∴∠BCE=∠ECD,∴∠E=∠BCE,∴BE=BC=5,∴AB=BE-AE=5-2=3,∴CD=3.故选 A.
3. C
4. B【解析】∵四边形 ABCD是平行四边形,∴AE∥BC,∴ ∠DEF=∠CBF.
在△DEF与△CBF中
∴DF=CF.∵EF=BF,∴四边形BCED为平行四边形,故A 选项不符合题意.
∵AE∥BC,∴∠AEB=∠CBF,∠CDE=∠DCB.
∵∠AEB=∠BCD,∴∠CBF=∠BCD,∠CDE=∠AEB,
∴CF=BF,EF=DF,∴不能判定四边形BCED为平行四边形,故B选项符合题意.
∵四边形ABCD是平行四边形,∴ AD∥BC,AB∥CD,∴DE∥CB,∠ABD=∠CDB.
又∵∠ABD=∠DCE,∴∠DCE=∠CDB,∴BD∥CE,∴四边形BCED为平行四边形,故C选项不符合题意.∵AE∥BC,∴∠DEC+∠BCE=180°.∵∠AEC=∠CBD,∴∠CBD+∠BCE= 180°,∴ EC∥DB,∴四边形 BCED为平行四边形,故D选项不符合题意.故选B.
5. B【解析】∵AB∥DC,∴△ABC与△ABD的关面积相等.∵AE∥BD,∴△BED与△ABD的找面积相等.∵ED∥BC找不到与△ABD等底等高的三角形,∴和△ABD的面积相等的三角形有△ABC,△BED,共2个.
6. C【解析】连接BE,如图,易得∠C+∠D=∠1+∠2.∵四边形ABEF中,∠A+∠ABE+∠BEF+∠F=360°,∴∠A+∠ABC+∠1+∠2+∠DEF+∠F=360°,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F= 360°.∵∠F= 90°,∴∠A+∠ABC+∠C+∠D+∠DEF=270°.故选C.
7. C【解析】∵△ABC是等腰三角形,AB=AC,∴∠B=∠C.
在△ADE 与△DAC中, ∠C,
∴∠B=∠E.∵DE=AC,AB=AC,∴AB=DE.
在四边形ABDE中,AB=DE,即一组对边相等,∠B=∠E,即一组对角相等,
但由于点D是底边 BC上异于BC 中点的一个点,∠ADC+∠DAE≠180°,
∴AE 与BC不平行,∴四边形ABDE不是平行四边形.故运用题图(不添加辅助线)可以说明“一组对边相等,一组对角相等的四边形是平行四边形”说法错误. 故选C.
8. A【解析】延长DE到点 F,使EF=DE,连接FC,DC,AF. AE=EC,则四边形ADCF是平行
四边形,∴ ,即CF∥BD,∴四边形DBCF是平行四边形,∴DF⊥BC,∴DE∥BC,
且 正确的证明顺序是②→③→①→④.
9. C【解析】如图,延长EG交AB于H.∵∠BMF=∠BGE= 90°,
∴ MF∥EH,∴∠BFM=∠BHE.
∵∠1=30°,∴∠BFM=∠BHE=60°.
∵在平行四边形 ABCD中,DC∥AB,∴∠DEH=∠BHE= 60°.
∵∠GEN= 45°,∴∠2= 180°-60°-45°=75°.故选C.
10. B【解析】∵四边形ABCD是平行四边形,∥DC.又∵BD=2AD,∴OB=BC= OD=DA.∵点E是OC 中点,∴ BE⊥AC,故①正确.∵E,F分别是OC,OD的中点,∴EF∥CD,点G是Rt△ABE斜边AB上的中点, AG= BG,无法证明 GE= GF,故②错误.
∵BG=EF,AB∥CD∥EF,∴四边形BGFE是平行四边形,∴ GF= BE,且 BG= EF,∴△BGE≌△FEG(SSS),故③正确.∵EF∥CD∥AB,∴∠BAC=∠ACD=∠AEF.∵AG=GE,∴∠GAE= ∠AEG,∴∠AEG=∠AEF,∴EA平分∠GEF,故④正确.故选B.
11.11【解析】设这个多边形的边数为 n.根据题意,得 解得n=11.
12.(1,2)【解析】∵O(0,0),A(3,0),∴OA=3.∵四边形OABC 是平行四边形,∴BC∥OA,BC=OA=3.∵B(4,2),∴点C的坐标为(4-3,2),即C(1,2).
13.36【解析】∵ 108°,△ABC 是等腰三角形,
∴∠BAC=∠BCA=36°.
14.26°【解析】∵四边形ABCD 是平行四边形,∴∠ABC=∠D=102°,AD=BC.
∵AD=AE=BE,∴ BC=AE= BE,∴∠EAB=∠EBA,∠BEC=∠ECB.
∵∠BEC=∠EAB+∠EBA=2∠EAB,∴∠ACB=2∠CAB,∴∠CAB+∠ACB=3∠CAB= 180°-∠ABC=180°-102°=78°,∴∠BAC=26°.故答案为26°.
15.4a+2b【解析】由翻折的性质可得∠ACE=∠ACB.∵∠ACE=2∠ECD,∴∠ACE=∠ACB=
2∠ECD.∵ 四边形 ABCD 是平行四边形,∴AD∥BC,AB ∥CD,∴ ∠FAC =∠ACB,
∴∠FAC=∠FCA,∠B+∠BCD= 180°,即∠B +∠ACE + ∠ACB +∠ECD = 180°,
∴∠ECD= 20°, ∠ACE = ∠ACB = 40°=∠FAC,∠CFD=∠FAC+∠FCA=80°=∠B=∠D,∴ AF= CF= CD= a,则 AD= a+b,∴平行四边形ABCD的周长为2AD+2CD=2(a+b)+2a=4a+2b.故答案为4a+2b.
16.112°【解析】∵点M,N,P分别是DE,BC,CD的中点,∴ MP 是△DEC的中位线,NP是
△DBC的中位线,∴
又∵BD=CE,∴MP=NP,∴∠PMN=∠PNM=34°,
∴∠MPN=180°-∠PMN-∠PNM=180°-34°-34°=112°.故答案为112°.
【解析】如图,延长CG交BE于点 H.
∵四边形ABCD是平行四边形,∴BC=AD=3,CD=AB=2,DC∥AB,
∴BF=BC+CF=3+2=5.∵△BEF是等边三角形,∴BF=BE=5.∵DC∥AB,∴∠CDG=∠HEG.
在△DCG和△EHG中 (ASA),
∴DC= EH= 2,CG= HG,∴BH=3.∵∠CBH=60°,BC=BH=3,∴△CBH是等边三角形,
∴
18.【解】(1)如图,△ADC 即为所求.
(2)如图, EFGH即为所求,DH=5.
19.【解】(1)补充表格如下.
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° …
(2)不存在.
理由: n为正整数,∴不存在一个正多边形,其中∠α=21°.
20.(1)【证明】∵ 点 D,E分别是AB,AC 的中点,∴DE 是△ABC的中位线,∴DE∥BC.
∴CD=AD=DB,∴∠BAC=∠DCA.
∵∠CEF=∠BAC,∴∠CEF=∠DCA,∴EF∥CD,∴四边形CDEF是平行四边形.
(2)【解】与△AED 面积相等的三角形有△AEF,△ECF,△EDC,△EDB.
21.(1)【证明】∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠ADB=∠CBD.
∵O是对角线BD的中点,∴OB=OD.在△BOF和△DOE中.
∴△BOF≌△DOE(ASA),∴DE=BF,∴DE-AD=BF-BC,∴AE=CF.
(2)【解】OC∥DF 且 理由如下:
∵AE=BC,AE=CF,∴CF=BC.∵OB=OD,∴OC是△BDF的中位线,
∴OC∥DF且
22.【解】(1)∵(m+n) +|n-12|=0, 解得
∴A(-12,0),B(0,12),∴OA=12,OB=12,
(2)如图(1),过点E作EM⊥x轴于 M,
∴∠MDE+∠DEM=90°.∵△BDE 是等腰直角三角形,∴DE=DB,∠BDE=90°,∴∠MDE+∠BDO=90°,∴∠DEM=∠BDO.
在△DEM和△BDO中 ∴△DEM≌△BDO(AAS),
∴EM=DO,MD=OB=OA=12,
∴AM=MD+AD= 12+AD,EM=DO=OA+AD=12+AD,∴EM=AM,∴∠MAE=45°=∠OAF,
∴OA=OF=12,∴F(0,-12).
(3)存在.点 P坐标为(28,-16)或(-28,-8)或(-28,40).
∵AD=4,∴OM=MD+AD+OA= 12+4+12=28,EM=DO=OA+AD=12+4=16,∴E(-28,16).
设点P的坐标为(a,b).
如图(2),当以BF为对角线时, 解得
此时点P 的坐标为(28,-16);
当以EF为对角线时, 解得
此时点 P 的坐标为(-28,-8);
当以BE为对角线时, 解得
此时点 P 的坐标为(-28,40).
综上,点 P 的坐标为(28,-16)或(-28,-8)或(-28,40).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
综合测试卷
一、选择题(每小题3分,共30分)
1.若正多边形的一个外角是45°,则该正多边形的内角和为( )
A.540° B.720° C.900° D.1080°
2.如图,在平行四边形ABCD中,AE=2,AD=5,∠BCD的平分线交BA的延长线于点 E,则 CD的长为( )
A.3 B.2.5 C.2 D.1.5
3.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
4.如图,E是 ABCD的边AD延长线上一点,连接BE交CD于点F,连接CE,BD,添加以下条件,不能判定四边形BCED为平行四边形的是( )
A. EF=BF B.∠AEB=∠BCD C.∠ABD=∠DCE D.∠AEC=∠CBD
第4题图 第5题图
5.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包括△ABD)有( )
A.1个 B.2个 C.3个 D.4个
6.如图,∠F=90°,∠A+∠B+∠C+∠D+∠E的度数为( )
A.90°
B.180°
C.270°
D.360°
7.如图,△ABC 是等腰三角形,且AB=AC,点D是底边 BC 上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一种说法是错误的( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一组对边平行的四边形是平行四边形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
8已知:点 D,E分别是△ABC的边 AB,AC的中点,如图所示.
求证:DE∥BC,且
证明:如图,延长DE 到点 F,使EF=DE,连接FC,DC,AF,AE=EC,则四边形ADCF是平行四边形,以下是排序错误的证明过程:①∴DF⊥BC;②∴CF⊥AD,即CF⊥BD;③∴四边形 DBCF是平行四边形;④∴DE∥BC,且 则正确的证明顺序应是()
A.②→③→①→④ B.②→①→③→④ C.①→③→④→② D.①→③→②→④
第8题图 第9题图
9.如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( )
A.55° B.65° C.75° D.85°
10.如图,平行四边形ABCD中,对角线 AC,BD相交于O,BD=2AD,E,F,G 分别是OC,OD,AB的中点,以下结论:①BE⊥AC;②EG=GF;③△EFG≌△GBE;④EA平分∠GEF,其中正确的是( )
A.①②③ B.①③④ C.①②④ D.②③④
二、填空题(每小题3分,共21分)
11.一个多边形外角和是内角和的 则这个多边形的边数为___________.
12.在平面直角坐标系xOy中,平行四边形OABC的三个顶点O(0,0),A(3,0),B(4,2),则其第四个顶点是___________.
13.用一条宽度相等的足够长的纸条打一个结(如图(1)所示),然后轻轻拉紧,压平就可以得到如图(2)所示的正五边形 ABCDE.图中,∠BAC=_____________°.
14.如图,AC 是 ABCD的对角线,点E在 AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是____________.
第14题图 第15题图
15.如图,将 ABCD沿对角线AC翻折,点 B落在点E处,CE交AD于点F,若∠B=80°, ∠ACE=2∠ECD,FC=a,FD=b,则 ABCD的周长为___________.
16.如图,在△ABC中,点 D,E分别在边 AB,AC上,且BD=CE,连接CD,DE,点M,N,P分别是DE,BC,CD的中点,∠PMN= 34°,则∠MPN 的度数是___________.
第16题图 第17题图
17.如图,平行四边形ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=3,AB=CF=2,则CG的长为____________.
三、解答题(共49分)
18.如图,方格纸中每个小正方形的边长均为1,△ABC的顶点和线段EF的端点均在小正方形的顶点上.
(1)在方格纸中画出△ADC,使△ADC与△ABC关于直线AC 对称(点D在小正方形的顶点上);
(2)在方格纸中画出以线段EF为一边的平行四边形 EFGH(点 G,点 H均在小正方形的顶点上),且平行四边形 EFGH的面积为4,连接DH,请直接写出线段DH的长.
19.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.
(1)将下面的表格补充完整.
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° …
(2)根据规律,是否存在一个正多边形,其中∠α=21° 若存在,请求出n的值,若不存在,请说明理由.
20.在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点, 点F在BC延长线上,连接EF,且∠CEF=∠BAC.
(1)如图(1),求证:四边形 CDEF 是平行四边形;
(2)如图(2),连接AF,BE,在不添加任何辅助线的情况下,请直接写出图(2)中所有与△AED面积相等的三角形(△AED除外).
21.如图,在平行四边形 ABCD中,O 是对角线BD的中点,过点O的直线EF分别交DA,BC的延长线于E,F,连接CO.
(1)求证:AE=CF;
(2)若AE=BC,试探究线段OC 与线段DF之间的关系,并说明理由.
22.如图,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且 m,n满足
(1)求 的值;
(2)D为OA延长线上一动点,以 BD为直角边作等腰直角三角形BDE,过E,A作直线,求直线EA与y轴交点F的坐标;
(3)在(2)的条件下,当AD=4时,在平面内是否存在一点 P,使以B,E,F,P为顶点的四边
形是平行四边形 如果存在,直接写出点P的坐标;若不存在,说明理由.
参考答案
1. D【解析】由题可知,正多边形的边数为360°÷45°=8,∴这个多边形是正八边形,∴该
多边形的内角和为(8-2)×180°=1 080°.故选D.
2. A【解析】∵四边形 ABCD是平行四边形,∴AB∥CD,AD= BC= 5,CD= AB,∴∠E=∠ECD.∵CE 平分∠BCD,∴∠BCE=∠ECD,∴∠E=∠BCE,∴BE=BC=5,∴AB=BE-AE=5-2=3,∴CD=3.故选 A.
3. C
4. B【解析】∵四边形 ABCD是平行四边形,∴AE∥BC,∴ ∠DEF=∠CBF.
在△DEF与△CBF中
∴DF=CF.∵EF=BF,∴四边形BCED为平行四边形,故A 选项不符合题意.
∵AE∥BC,∴∠AEB=∠CBF,∠CDE=∠DCB.
∵∠AEB=∠BCD,∴∠CBF=∠BCD,∠CDE=∠AEB,
∴CF=BF,EF=DF,∴不能判定四边形BCED为平行四边形,故B选项符合题意.
∵四边形ABCD是平行四边形,∴ AD∥BC,AB∥CD,∴DE∥CB,∠ABD=∠CDB.
又∵∠ABD=∠DCE,∴∠DCE=∠CDB,∴BD∥CE,∴四边形BCED为平行四边形,故C选项不符合题意.∵AE∥BC,∴∠DEC+∠BCE=180°.∵∠AEC=∠CBD,∴∠CBD+∠BCE= 180°,∴ EC∥DB,∴四边形 BCED为平行四边形,故D选项不符合题意.故选B.
5. B【解析】∵AB∥DC,∴△ABC与△ABD的关面积相等.∵AE∥BD,∴△BED与△ABD的找面积相等.∵ED∥BC找不到与△ABD等底等高的三角形,∴和△ABD的面积相等的三角形有△ABC,△BED,共2个.
6. C【解析】连接BE,如图,易得∠C+∠D=∠1+∠2.∵四边形ABEF中,∠A+∠ABE+∠BEF+∠F=360°,∴∠A+∠ABC+∠1+∠2+∠DEF+∠F=360°,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F= 360°.∵∠F= 90°,∴∠A+∠ABC+∠C+∠D+∠DEF=270°.故选C.
7. C【解析】∵△ABC是等腰三角形,AB=AC,∴∠B=∠C.
在△ADE 与△DAC中, ∠C,
∴∠B=∠E.∵DE=AC,AB=AC,∴AB=DE.
在四边形ABDE中,AB=DE,即一组对边相等,∠B=∠E,即一组对角相等,
但由于点D是底边 BC上异于BC 中点的一个点,∠ADC+∠DAE≠180°,
∴AE 与BC不平行,∴四边形ABDE不是平行四边形.故运用题图(不添加辅助线)可以说明“一组对边相等,一组对角相等的四边形是平行四边形”说法错误. 故选C.
8. A【解析】延长DE到点 F,使EF=DE,连接FC,DC,AF. AE=EC,则四边形ADCF是平行
四边形,∴ ,即CF∥BD,∴四边形DBCF是平行四边形,∴DF⊥BC,∴DE∥BC,
且 正确的证明顺序是②→③→①→④.
9. C【解析】如图,延长EG交AB于H.∵∠BMF=∠BGE= 90°,
∴ MF∥EH,∴∠BFM=∠BHE.
∵∠1=30°,∴∠BFM=∠BHE=60°.
∵在平行四边形 ABCD中,DC∥AB,∴∠DEH=∠BHE= 60°.
∵∠GEN= 45°,∴∠2= 180°-60°-45°=75°.故选C.
10. B【解析】∵四边形ABCD是平行四边形,∥DC.又∵BD=2AD,∴OB=BC= OD=DA.∵点E是OC 中点,∴ BE⊥AC,故①正确.∵E,F分别是OC,OD的中点,∴EF∥CD,点G是Rt△ABE斜边AB上的中点, AG= BG,无法证明 GE= GF,故②错误.
∵BG=EF,AB∥CD∥EF,∴四边形BGFE是平行四边形,∴ GF= BE,且 BG= EF,∴△BGE≌△FEG(SSS),故③正确.∵EF∥CD∥AB,∴∠BAC=∠ACD=∠AEF.∵AG=GE,∴∠GAE= ∠AEG,∴∠AEG=∠AEF,∴EA平分∠GEF,故④正确.故选B.
11.11【解析】设这个多边形的边数为 n.根据题意,得 解得n=11.
12.(1,2)【解析】∵O(0,0),A(3,0),∴OA=3.∵四边形OABC 是平行四边形,∴BC∥OA,BC=OA=3.∵B(4,2),∴点C的坐标为(4-3,2),即C(1,2).
13.36【解析】∵ 108°,△ABC 是等腰三角形,
∴∠BAC=∠BCA=36°.
14.26°【解析】∵四边形ABCD 是平行四边形,∴∠ABC=∠D=102°,AD=BC.
∵AD=AE=BE,∴ BC=AE= BE,∴∠EAB=∠EBA,∠BEC=∠ECB.
∵∠BEC=∠EAB+∠EBA=2∠EAB,∴∠ACB=2∠CAB,∴∠CAB+∠ACB=3∠CAB= 180°-∠ABC=180°-102°=78°,∴∠BAC=26°.故答案为26°.
15.4a+2b【解析】由翻折的性质可得∠ACE=∠ACB.∵∠ACE=2∠ECD,∴∠ACE=∠ACB=
2∠ECD.∵ 四边形 ABCD 是平行四边形,∴AD∥BC,AB ∥CD,∴ ∠FAC =∠ACB,
∴∠FAC=∠FCA,∠B+∠BCD= 180°,即∠B +∠ACE + ∠ACB +∠ECD = 180°,
∴∠ECD= 20°, ∠ACE = ∠ACB = 40°=∠FAC,∠CFD=∠FAC+∠FCA=80°=∠B=∠D,∴ AF= CF= CD= a,则 AD= a+b,∴平行四边形ABCD的周长为2AD+2CD=2(a+b)+2a=4a+2b.故答案为4a+2b.
16.112°【解析】∵点M,N,P分别是DE,BC,CD的中点,∴ MP 是△DEC的中位线,NP是
△DBC的中位线,∴
又∵BD=CE,∴MP=NP,∴∠PMN=∠PNM=34°,
∴∠MPN=180°-∠PMN-∠PNM=180°-34°-34°=112°.故答案为112°.
【解析】如图,延长CG交BE于点 H.
∵四边形ABCD是平行四边形,∴BC=AD=3,CD=AB=2,DC∥AB,
∴BF=BC+CF=3+2=5.∵△BEF是等边三角形,∴BF=BE=5.∵DC∥AB,∴∠CDG=∠HEG.
在△DCG和△EHG中 (ASA),
∴DC= EH= 2,CG= HG,∴BH=3.∵∠CBH=60°,BC=BH=3,∴△CBH是等边三角形,
∴
18.【解】(1)如图,△ADC 即为所求.
(2)如图, EFGH即为所求,DH=5.
19.【解】(1)补充表格如下.
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° …
(2)不存在.
理由: n为正整数,∴不存在一个正多边形,其中∠α=21°.
20.(1)【证明】∵ 点 D,E分别是AB,AC 的中点,∴DE 是△ABC的中位线,∴DE∥BC.
∴CD=AD=DB,∴∠BAC=∠DCA.
∵∠CEF=∠BAC,∴∠CEF=∠DCA,∴EF∥CD,∴四边形CDEF是平行四边形.
(2)【解】与△AED 面积相等的三角形有△AEF,△ECF,△EDC,△EDB.
21.(1)【证明】∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠ADB=∠CBD.
∵O是对角线BD的中点,∴OB=OD.在△BOF和△DOE中.
∴△BOF≌△DOE(ASA),∴DE=BF,∴DE-AD=BF-BC,∴AE=CF.
(2)【解】OC∥DF 且 理由如下:
∵AE=BC,AE=CF,∴CF=BC.∵OB=OD,∴OC是△BDF的中位线,
∴OC∥DF且
22.【解】(1)∵(m+n) +|n-12|=0, 解得
∴A(-12,0),B(0,12),∴OA=12,OB=12,
(2)如图(1),过点E作EM⊥x轴于 M,
∴∠MDE+∠DEM=90°.∵△BDE 是等腰直角三角形,∴DE=DB,∠BDE=90°,∴∠MDE+∠BDO=90°,∴∠DEM=∠BDO.
在△DEM和△BDO中 ∴△DEM≌△BDO(AAS),
∴EM=DO,MD=OB=OA=12,
∴AM=MD+AD= 12+AD,EM=DO=OA+AD=12+AD,∴EM=AM,∴∠MAE=45°=∠OAF,
∴OA=OF=12,∴F(0,-12).
(3)存在.点 P坐标为(28,-16)或(-28,-8)或(-28,40).
∵AD=4,∴OM=MD+AD+OA= 12+4+12=28,EM=DO=OA+AD=12+4=16,∴E(-28,16).
设点P的坐标为(a,b).
如图(2),当以BF为对角线时, 解得
此时点P 的坐标为(28,-16);
当以EF为对角线时, 解得
此时点 P 的坐标为(-28,-8);
当以BE为对角线时, 解得
此时点 P 的坐标为(-28,40).
综上,点 P 的坐标为(28,-16)或(-28,-8)或(-28,40).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
