直线与圆的位置关系复习(浙江省台州市路桥区)
文档属性
| 名称 | 直线与圆的位置关系复习(浙江省台州市路桥区) |
|
|
| 格式 | rar | ||
| 文件大小 | 290.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-21 00:00:00 | ||
图片预览


文档简介
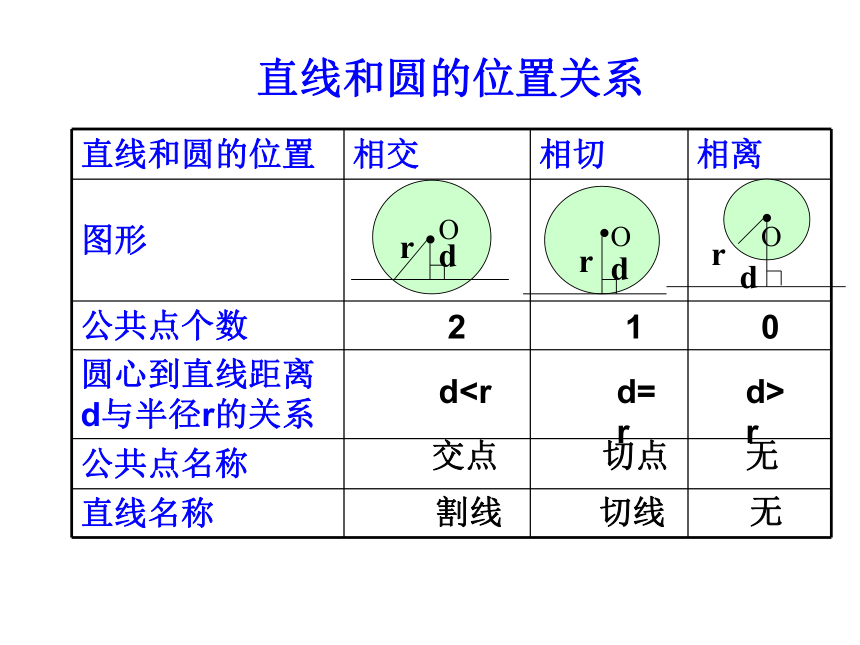
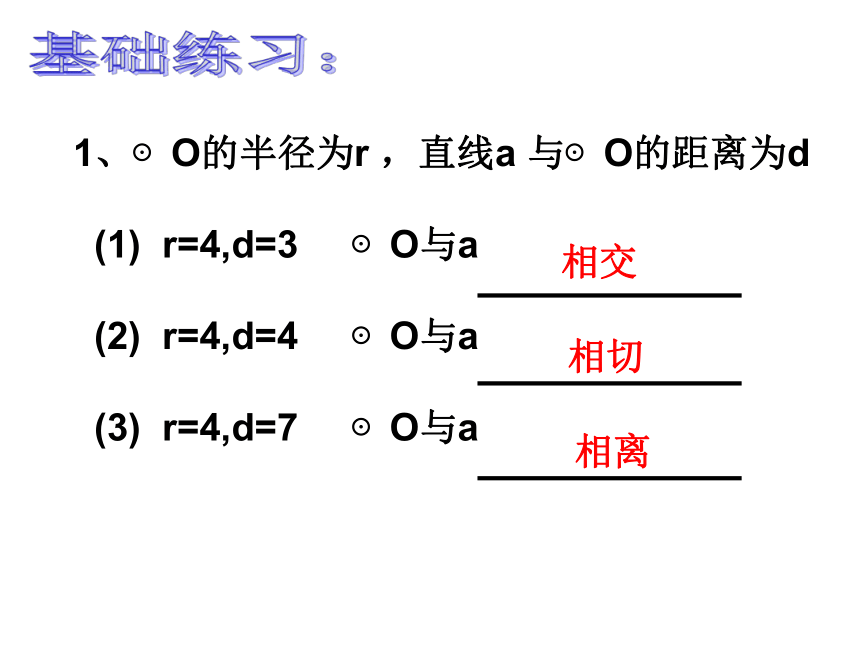
课件19张PPT。直线与圆的位置关系复习课直线和圆的位置关系 210dr交点切点无 割线 切线 无O?drOl?drO ?dr1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
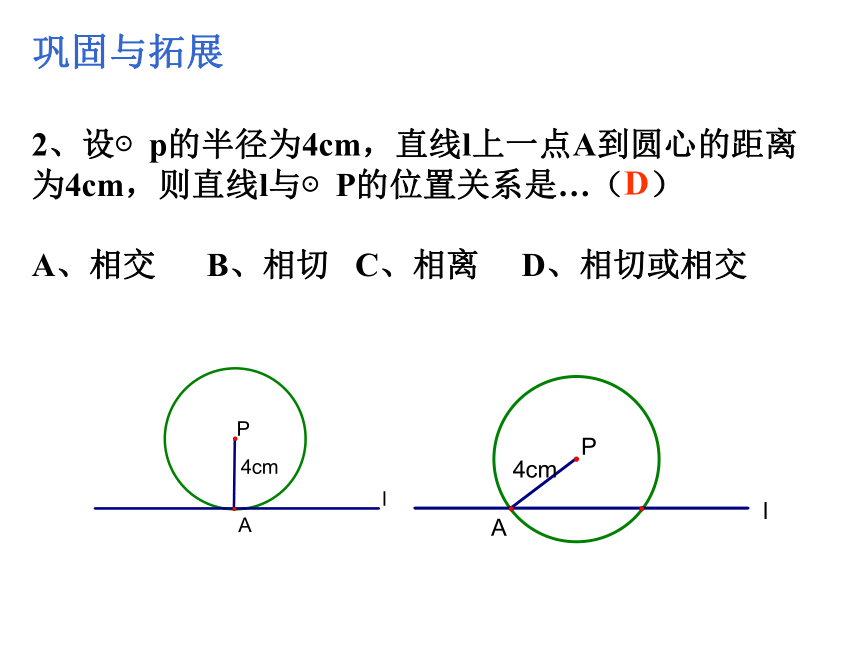
(3) r=4,d=7 ⊙O与a 相离相交相切基础练习:2、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙P的位置关系是…( )
A、相交 B、相切 C、相离 D、相切或相交D巩固与拓展切线的判定方法有:③、切线的判定定理。②、比较法(d=r):
直线到圆心的距离等于圆的半径。①、定义法: 直线与圆有一个公共点。切线的判定定理:经过半径外端
并且垂直于这条半径的直线是圆
的切线。判断下图直线l是否是⊙O的切线?
并说明为什么。证明一条直线为圆的切线时,必须两个条件缺一不可:①过半径外端
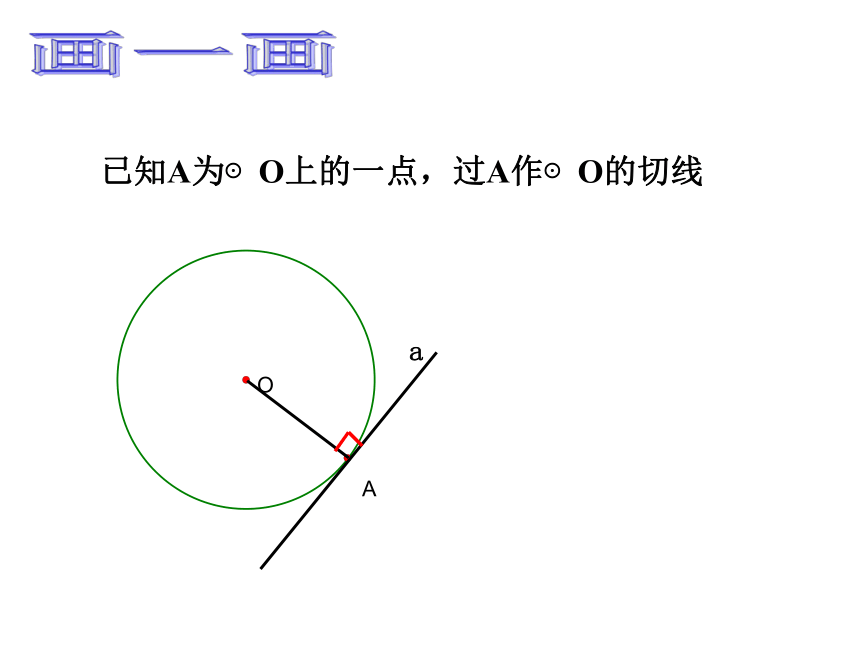
②垂直于这条半径。辨一辨已知A为⊙O上的一点,过A作⊙O的切线画一画切线的性质:
1、圆的切线垂直过切点的半径
2、经过切点垂直于切线的直线必经过圆心.3.(05,湖州)如图,A,B是⊙O的两点,AC是⊙O的切线,∠B=65°则∠BAC=( ) A、35° B、25°C、50° D、65°B基础练习4、(05,温州)已知:PA为⊙O的切线,A为切点,OB交⊙O于点B ,PB=2,PA =4. ⊙O的半径r=巩固与拓展:24rr3切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.条件:PA, PB切⊙O于
A、B两点,结论:⑴ PA=PB ⑵∠OPA=∠OPB若连结两切点A,B,AB交OP于点M,又能得到什么新的结论?MOP垂直平分AB如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,∠ABC=___基础练习如图,∠APC=50°,PA、PC、DE都为⊙O的切线,则∠DOE为 。 变式:改变切线DE的位置,则∠DOE=___F65°65°若PA=2,则△ PED的周长为 ___ 若改变切线DE的位置呢?4思考与探索:1、如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E. 由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
(2)⊙O上是否存在点C,使△ PBC为等边三角形?若存在,请求出此时PB的值,若不存在,请说明理由。 2、已知,如图,A是半径为2的⊙O上一点,P是OA延长线上的动点,过P点作⊙O的切线为B.(1)当PB=4时,求PO 的值。 C思考与探索:DOAPB2、如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G, ⊙O 是△CGF的外接圆
求证:CE是⊙O的切线。 思考与探索:1234课堂小结1 今天我们一起复习哪些圆的有关知识?
2 今天我们探究的问题都有什么特点?
3 对今天的问题你还有什么困惑?
4 今天你有什么收获吗? 谢谢指导
再见 8、如图,园林部门准备在公园的三条小道围成的地块内建造一个圆形喷水池,要求面积尽量大。请问如何建造圆的面积最大?当圆的面积最大时,圆的半径是多少?思考与探索:ABCOr
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
(3) r=4,d=7 ⊙O与a 相离相交相切基础练习:2、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙P的位置关系是…( )
A、相交 B、相切 C、相离 D、相切或相交D巩固与拓展切线的判定方法有:③、切线的判定定理。②、比较法(d=r):
直线到圆心的距离等于圆的半径。①、定义法: 直线与圆有一个公共点。切线的判定定理:经过半径外端
并且垂直于这条半径的直线是圆
的切线。判断下图直线l是否是⊙O的切线?
并说明为什么。证明一条直线为圆的切线时,必须两个条件缺一不可:①过半径外端
②垂直于这条半径。辨一辨已知A为⊙O上的一点,过A作⊙O的切线画一画切线的性质:
1、圆的切线垂直过切点的半径
2、经过切点垂直于切线的直线必经过圆心.3.(05,湖州)如图,A,B是⊙O的两点,AC是⊙O的切线,∠B=65°则∠BAC=( ) A、35° B、25°C、50° D、65°B基础练习4、(05,温州)已知:PA为⊙O的切线,A为切点,OB交⊙O于点B ,PB=2,PA =4. ⊙O的半径r=巩固与拓展:24rr3切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.条件:PA, PB切⊙O于
A、B两点,结论:⑴ PA=PB ⑵∠OPA=∠OPB若连结两切点A,B,AB交OP于点M,又能得到什么新的结论?MOP垂直平分AB如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,∠ABC=___基础练习如图,∠APC=50°,PA、PC、DE都为⊙O的切线,则∠DOE为 。 变式:改变切线DE的位置,则∠DOE=___F65°65°若PA=2,则△ PED的周长为 ___ 若改变切线DE的位置呢?4思考与探索:1、如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E. 由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
(2)⊙O上是否存在点C,使△ PBC为等边三角形?若存在,请求出此时PB的值,若不存在,请说明理由。 2、已知,如图,A是半径为2的⊙O上一点,P是OA延长线上的动点,过P点作⊙O的切线为B.(1)当PB=4时,求PO 的值。 C思考与探索:DOAPB2、如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G, ⊙O 是△CGF的外接圆
求证:CE是⊙O的切线。 思考与探索:1234课堂小结1 今天我们一起复习哪些圆的有关知识?
2 今天我们探究的问题都有什么特点?
3 对今天的问题你还有什么困惑?
4 今天你有什么收获吗? 谢谢指导
再见 8、如图,园林部门准备在公园的三条小道围成的地块内建造一个圆形喷水池,要求面积尽量大。请问如何建造圆的面积最大?当圆的面积最大时,圆的半径是多少?思考与探索:ABCOr
同课章节目录
