数学人教A版(2019)选择性必修第一册1.4空间向量的应用(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4空间向量的应用(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 10:58:24 | ||
图片预览






文档简介
(共19张PPT)
1.4空间向量的应用
点的向量表示
如何用向量表示空间中的一个点
如图1.4-1,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示我们把向量称为点P的位置向量.
我们知道,空间中给定一个点 A 和一个方向就能唯一确定一条直线l.如何用向量表示直线l
空间直线的向量表示
如图1.4-2,a 是直线的方向向量,在直线上取=a,设P是直线上的任意一点,由向量共线的条件可知,点P在直线上的充要条件是存在实数t,使得
=ta,即=t
如图1.4-3,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
=+ta,
将=a代人上式,得
=+t,
空间直线的向量表示
平面的向量表示
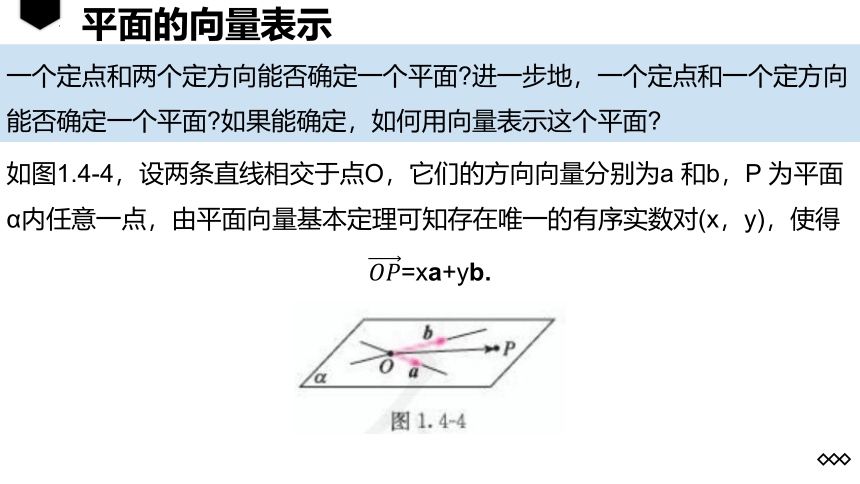
一个定点和两个定方向能否确定一个平面 进一步地,一个定点和一个定方向能否确定一个平面 如果能确定,如何用向量表示这个平面
如图1.4-4,设两条直线相交于点O,它们的方向向量分别为a 和b,P 为平面α内任意一点,由平面向量基本定理可知存在唯一的有序实数对(x,y),使得
=xa+yb.
平面的向量表示
如图1.4-5,取定空间任意一点 O,可以得到,空间一点P位于平面ABC内的充要条件是存在实数x,y,使
=+x+y.
平面的向量表示
如图1.4-6,直线L⊥α,取直线的方向向量a,我们称向量a为平面α的法向量(normalvector),给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合{P|a·=0}.
由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系
空间中直线、平面的平行
如图1.4-8,设u1,u2 分别是直线l1,l2的方向向量.由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行.所以
l1∥l2 u1∥u2 存在λ∈R,使得u1=λu2.
空间中直线、平面的平行
如图1.4-9,设u是直线的方向向量,n是平面α的法向量,l不在α内,则
l//α u⊥n u·n=0.
如图1.4-10,设n1,n2分别是平面α,β的法向量,则
α//β n1//n2 存在λ∈R,使得n1=λn2.
空间中直线、平面的垂直
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系
如图1.4-13(1),设直线l1,l2的方向向量分别为u1,u2,则
l1⊥l2 u1⊥u2 u1·u2=0.
空间中直线、平面的垂直
如图1.4-13(2),设直线l的方向向量为u,平面α的
法向量为n,则
l⊥α u∥n 存在λ∈R,使得u=λn
如图1.4-13(3),设平面α,β的法向量分别为n1,n2,则
α⊥β n1⊥n2 n1·n2=0.
1.已知平面α的一个法向量是(2,-1,1),α∥β,则下列向量可作为平面β的法向量的是( )
A.(4,2,-2) B.(2,0,4) C.(2,-1,-5) D.(4,-2,2)
课堂练习
2.已知平面α内两向量a=(1,1,1),b=(0,2,-1),且c=ma+nb+(4,-4,1),
若c为平面α的法向量,则m,n的值分别为( )
A.-1,2 B.1,-2 C.1,2 D.-1,-2
课堂练习
3.设直线l与平面α相交,且l的方向向量为a,α的法向量为n,若〈a,n〉=π,则l与α所成的角为( )
A. B. C. D.
课堂练习
4.已知A(0,1,1),B(0,2,0),C(3,0,0),O(0,0,0),则点O到平面ABC的距离是( )
A. B. C. D.
课堂练习
5.如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证: AA1⊥平面ABC;
(2)求平面A1C1B与平面B1C1B夹角的余弦值.
课堂练习
学生回顾思考知识点;教师补充归纳总结
课堂小结
课时作业1.4
布置作业
谢谢!
1.4空间向量的应用
点的向量表示
如何用向量表示空间中的一个点
如图1.4-1,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示我们把向量称为点P的位置向量.
我们知道,空间中给定一个点 A 和一个方向就能唯一确定一条直线l.如何用向量表示直线l
空间直线的向量表示
如图1.4-2,a 是直线的方向向量,在直线上取=a,设P是直线上的任意一点,由向量共线的条件可知,点P在直线上的充要条件是存在实数t,使得
=ta,即=t
如图1.4-3,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
=+ta,
将=a代人上式,得
=+t,
空间直线的向量表示
平面的向量表示
一个定点和两个定方向能否确定一个平面 进一步地,一个定点和一个定方向能否确定一个平面 如果能确定,如何用向量表示这个平面
如图1.4-4,设两条直线相交于点O,它们的方向向量分别为a 和b,P 为平面α内任意一点,由平面向量基本定理可知存在唯一的有序实数对(x,y),使得
=xa+yb.
平面的向量表示
如图1.4-5,取定空间任意一点 O,可以得到,空间一点P位于平面ABC内的充要条件是存在实数x,y,使
=+x+y.
平面的向量表示
如图1.4-6,直线L⊥α,取直线的方向向量a,我们称向量a为平面α的法向量(normalvector),给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合{P|a·=0}.
由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系
空间中直线、平面的平行
如图1.4-8,设u1,u2 分别是直线l1,l2的方向向量.由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行;反过来,如果两条直线的方向向量平行,那么这两条直线也平行.所以
l1∥l2 u1∥u2 存在λ∈R,使得u1=λu2.
空间中直线、平面的平行
如图1.4-9,设u是直线的方向向量,n是平面α的法向量,l不在α内,则
l//α u⊥n u·n=0.
如图1.4-10,设n1,n2分别是平面α,β的法向量,则
α//β n1//n2 存在λ∈R,使得n1=λn2.
空间中直线、平面的垂直
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系
如图1.4-13(1),设直线l1,l2的方向向量分别为u1,u2,则
l1⊥l2 u1⊥u2 u1·u2=0.
空间中直线、平面的垂直
如图1.4-13(2),设直线l的方向向量为u,平面α的
法向量为n,则
l⊥α u∥n 存在λ∈R,使得u=λn
如图1.4-13(3),设平面α,β的法向量分别为n1,n2,则
α⊥β n1⊥n2 n1·n2=0.
1.已知平面α的一个法向量是(2,-1,1),α∥β,则下列向量可作为平面β的法向量的是( )
A.(4,2,-2) B.(2,0,4) C.(2,-1,-5) D.(4,-2,2)
课堂练习
2.已知平面α内两向量a=(1,1,1),b=(0,2,-1),且c=ma+nb+(4,-4,1),
若c为平面α的法向量,则m,n的值分别为( )
A.-1,2 B.1,-2 C.1,2 D.-1,-2
课堂练习
3.设直线l与平面α相交,且l的方向向量为a,α的法向量为n,若〈a,n〉=π,则l与α所成的角为( )
A. B. C. D.
课堂练习
4.已知A(0,1,1),B(0,2,0),C(3,0,0),O(0,0,0),则点O到平面ABC的距离是( )
A. B. C. D.
课堂练习
5.如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证: AA1⊥平面ABC;
(2)求平面A1C1B与平面B1C1B夹角的余弦值.
课堂练习
学生回顾思考知识点;教师补充归纳总结
课堂小结
课时作业1.4
布置作业
谢谢!
