吉林长春市九年级上册集体备课:核心素养下的几何模型教学策略 课件(65张PPT)
文档属性
| 名称 | 吉林长春市九年级上册集体备课:核心素养下的几何模型教学策略 课件(65张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 10:15:20 | ||
图片预览







文档简介
(共65张PPT)
核心素养下的几何模型教学策略
(九年级数学)
一、数学核心素养
会用数学的眼光观察现实世界
抽象能力、几何直观、
空间观念、创新意识
一、数学核心素养
会用数学的思维思考现实世界
运算能力、推理能力
一、数学核心素养
会用数学的语言表达现实世界
数据意识、模型意识、应用意识
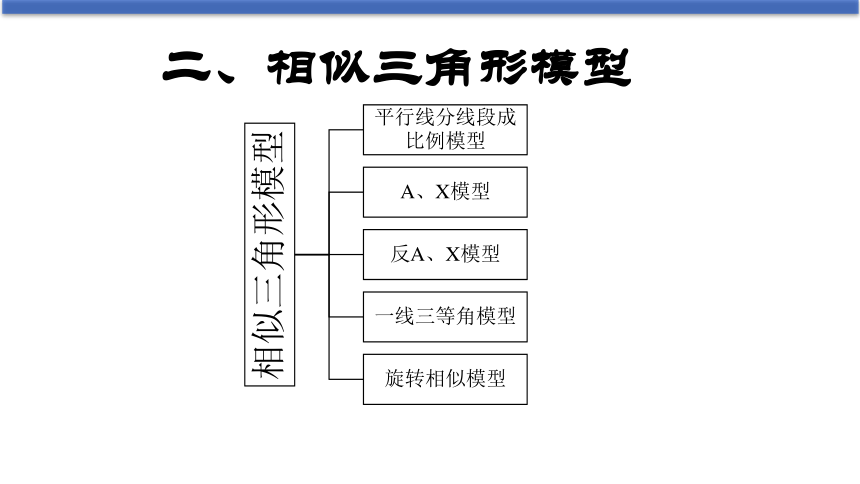
二、相似三角形模型
1.平行线分线段成比例模型
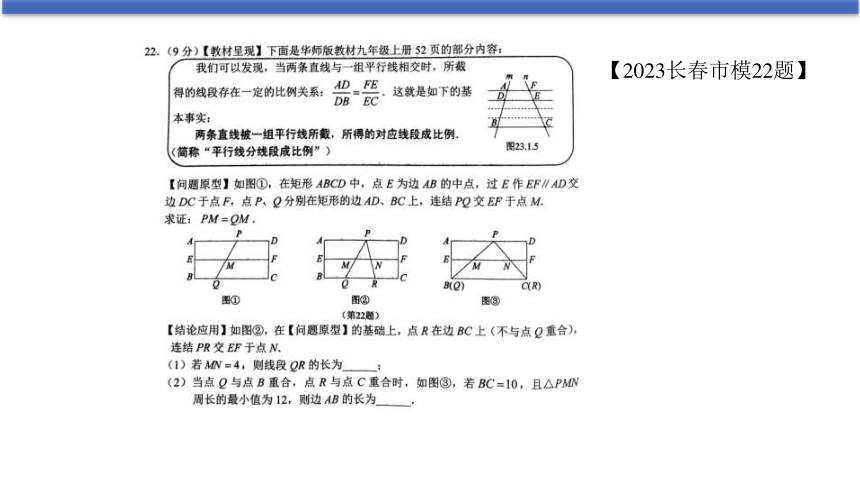
我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系:
这就是如下的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.(简称:平行线分线段成比例)
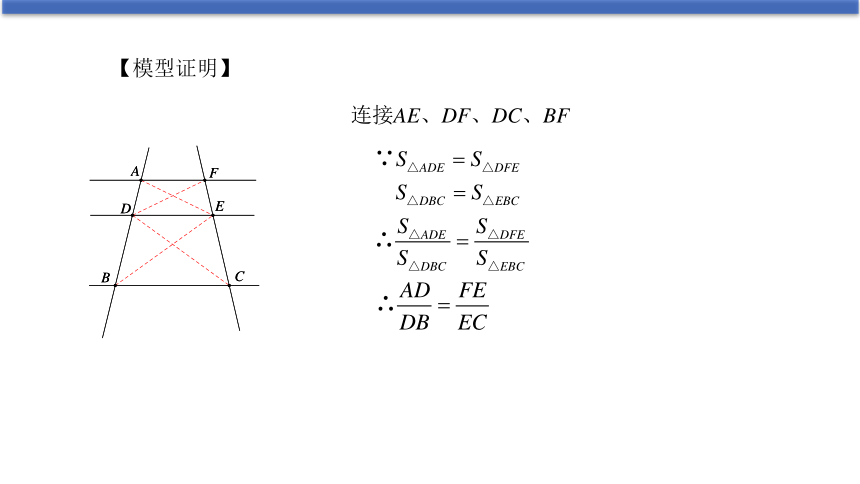
【模型证明】
连接AE、DF、DC、BF
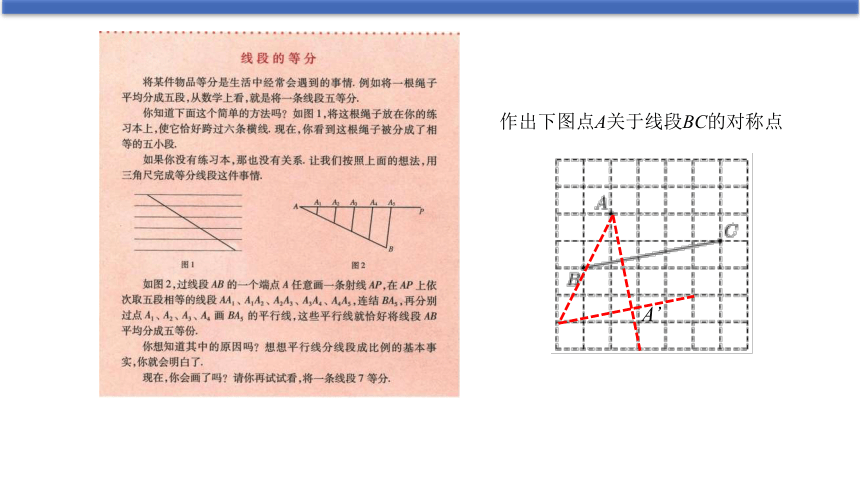
作出下图点A关于线段BC的对称点
A’
【2023长春市模22题】
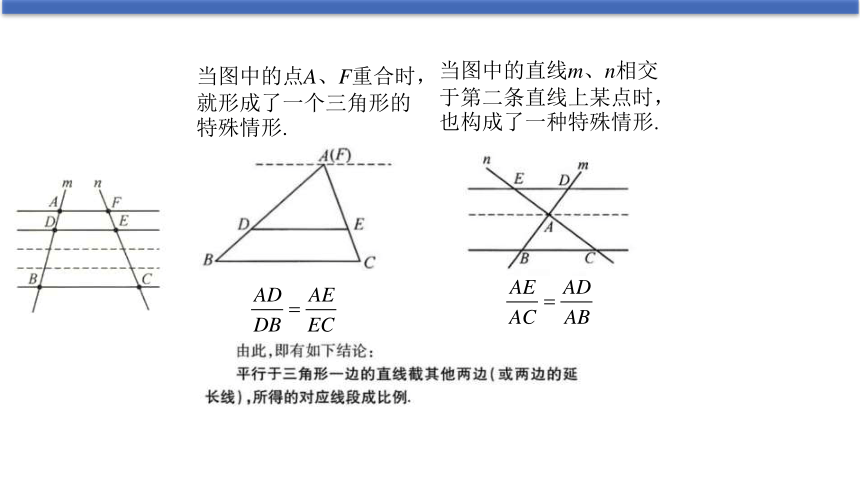
当图中的点A、F重合时,就形成了一个三角形的特殊情形.
当图中的直线m、n相交于第二条直线上某点时,也构成了一种特殊情形.
2. A、X模型
A型
X型
已知:DE∥BC
结论:△ADE∽△ABC
在相似三角形的判定中,我们常通过作平行线、从而得出A型或X型相似.
【模型证明】
过D作DF∥AC,交BC于点F
【模型证明】
过E作EF∥BC,交CB延长线于点F
已知:
求:BE的长(用含a、b、m、n的式子表示)
令
【模型拓展:梯形中位线证明】
【模型拓展:倒数模型】
【模型拓展:角平分线分线段成比例】
【模型拓展:角平分线分线段成比例】
过点C作AD的平行线,与BA延长线交于点E
【模型拓展:角平分线分线段成比例】
15°的各个三角函数值也可以利用此方法计算
【模型拓展:12345模型】
【模型拓展:12345模型】
以15°为例,简单介绍一下计算方法
【模型拓展:梅氏定理】
【模型拓展:梅氏定理】
过D作DH∥CF交AB于点H
【模型拓展:重心模型】
在△ABC中,D、E、分别是BC、AC中点,连结AD、
BE交于点F,证明:
【模型拓展】证明三角形三条中线交于一点
【模型拓展】
模型结论:
3. 反A、X模型
模型结论:
黄金三角形
顶角为36°的等腰三角形,底边与腰长的比∠C的平分线,交AB于D,D为AB的黄金分割点。
模型结论:
模型结论:
反“X”模型
条件:∠A=∠C
【模型拓展:托勒密定理】
【与圆有关的相似】
相交弦定理
割线定理
切割线定理
4. 一线三等角模型
模型结论:
【锐角型】
如图,等腰△ABC,∠DEF=∠B=∠C
【模型证明】
4. 一线三等角模型
模型结论:
【钝角型】
如图,四边形ABCD中,∠DEC=∠A=∠B
【模型证明】
4. 一线三等角模型
【直角型】
如图,A、B、C三点共线,∠A=∠C=∠DBE=90°,用同样的方法,易证△ABD∽△CEB,直角型的一线三等角我们又叫做“三垂直模型”,它的应用更加广泛,考试出现概率最大
4. 一线三等角模型
同样可以证明两个三角形相似
正方形ABCD边长为5,点P、Q分别在直线CB、DC上(点P不与点C、B重合),且保持∠APQ=90°.当CQ=1时,求线段BP的长.
针对点P在直线CB上的位置进行分类讨论
点P在线段BC上
点P在线段CB延长线上
点P在线段BC延长线上
【模型应用】
5. 旋转相似模型
如图,已知DE∥BC,将△ADE绕点A旋转一定角度,连接BD、CE.
旋转△ADE
△ADE∽△ABC
△ABD∽△ACE
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
【模型应用】直接应用旋转相似
【模型应用】构造旋转相似模型
如图,在△ABC中,∠BAC=2∠DBC=60°,D为△ABC内一点,连接DA、DB、DC,若∠BDC=90°, ,AC=6,则AB的长为?
将△ADC绕点D顺时针旋转90°,并放大 倍.
【模型应用】构造旋转相似模型
如图,在△ABC中,∠BAC=2∠DBC=60°,D为△ABC内一点,连接DA、DB、DC,若∠BDC=90°, ,AC=6,则AB的长为?
将△ADC绕点C顺时针旋转90°,并放大2倍.
【模型拓展】瓜豆模型
△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当点P在直线l上运动时,Q的轨迹是?
【模型拓展】瓜豆模型
△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当点P在圆O上运动时,Q的轨迹是?
三、圆的相关模型
1.连半径构造等腰三角形模型
已知AB是圆O的一条弦,连结OA、OB,则∠A=∠B.
在圆的相关题目中,不要忽略隐含的已知条件,我们通常可以连结半径构造等腰三角形,利用等腰三角形的性质及圆中的相关定理,解决角度的计算问题.
如图,AB是圆O的直径,弦PQ交AB于M,且PM=MO.求证:
如图,连接OP、OQ
∵PM=OM,
∴∠P=∠MOP.
∵OP=OQ,
∴∠P=∠Q.
∵∠QMO=2∠MOP,
∴∠BOQ=3∠MOP.
∴∠AOP=∠BOQ.
∴
2.构造直角三角形模型
当图形中含有直径时,构造直径所对的圆周角是解决问题的重要思路,在证明有关问题中注意90°圆周角的构造.
在解决求弦长,弦心距,半径问题时,在圆中常作弦心距或连接半径作为辅助线,利用弦心距、半径和半弦组成一个直角三角形,再利用勾股定理进行计算
如图,AB是圆O的直径,AB=AC,BC交圆O于点D,AC交圆O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
(1)
(2)
连接AD
已知圆O的直径AB和弦CD相交于点E,AE=2,BE=6,∠DEB=60°.求CD的长
过点O作OF⊥CD于点F,连接OD.
3.与圆的切线有关的辅助线
(1)已知切线:连接过切点的半径.如图,已知直线AB是圆O的切线,点C是切点.连接OC,则OC⊥AB.
(2)证明切线:
①当已知直线经过圆上的一点时,连半径,证垂直.
②如果不知道直线与圆是否有交点时,作垂直,证明 垂线段长度等于半径.
如图,OA、OB是圆O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交圆O于点Q,过Q点的切线交OA延长线于R点.求证:RP=RQ.
如图,连接OQ.
∵OQ=OB,
∴∠OQB=∠OBQ.
∵RQ为圆O的切线,OA⊥OB,
∴∠BPO=90°-∠OBQ,∠BQR=90°-∠OQB.
∴∠BPO=∠QPR=∠BQR.
∴RP=RQ
如图,△ABC内接于圆O,过点A作直线DE,当∠BAE=∠C时,试确定直线DE与圆O的位置关系,并证明你的结论.
直线DE与圆O相切,理由如下:
如图,连接AO并延长,交圆O于点F,连接BF.
∵∠BAE=∠C,∠C=∠F,
∴∠BAE=∠F.
∵AF为直径,
∴∠ABF=90°.
∴∠F+∠BAF=90°.
∴∠BAE+∠BAF=90°.
∴FA⊥DE.
∵AO是圆O的半径,
∴直线DE与圆O相切.
如图,AB是圆O的直径,AC是它的切线,CO平分∠ACD.求证:CD是圆O的切线.
如图,过点O作OE⊥CD于点E.
∵AC是圆O的切线,
∴OA⊥AC.
∵CO平分∠ACD,OE⊥CD,
∴OA=OE.
∴CD是圆O的切线.
辅助圆模型
【模型一】共端点,等线段模型
图①
图②
图③
如图①,出现“共端点,等线段”时,可利用圆的定义构造辅助圆.
如图②,若OA=OB=OC,则A、B、C三点在以O为圆心,OA为半径的圆上.
如图③,∠ACB=1/2∠AOB,∠BAC=1/2∠BOC.
如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD.
求证:∠1+∠2=90°.
∵AB=AC=AD,
∴B、C、D在以A为圆心,AB为半径的圆A上.
∴∠BAC=2∠1.
∵AB=AC,
∴∠ABC=∠2.
在△ABC中,
∵∠BAC+∠ABC+∠2=180°,
∴2∠1+2∠2=180°.
∴∠1+∠2=90°.
辅助圆模型
【模型二】直角三角形共斜边模型
(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆.
(2)四点共圆后,可以根据圆周角定理得到角度相等,完成角度等量关系转化,是证明角度相等的重要途径之一。
如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外角平分线于点F,求证:FE=DE.
连接DB、DF.
∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,
∴∠CBF=45°,∠DBC=45°,
∴∠DBF=90°.
又∵∠DEF=90°,
∴D、E、B、F四点共圆.
∴∠DFE=∠DBE=45°.
∴△DEF是等腰直角三角形.
∴FE=DE.
如图,BE、CF为△ABC的高,且交于点H,连接AH并延长交BC于点D.求证:AD⊥BC.
【模型拓展】三角形三条高线交于一点
连接EF.
∵Rt△AFH和Rt△AEH共斜边AH,
∴A、F、H、E四点共圆.
∴∠1=∠2.
∵Rt△BCF和Rt△BEC共斜边BC,
∴F、B、C、E四点共圆.
∴∠1=∠3.
∴∠2=∠3
∵∠3+∠ABD=90°,
∴∠2+∠ABD=90°
∴AD⊥BC.
总之,几何是数学教学的重要组成部分,也是数学教学的难点。在几何教学中采用模型教学具有重要意义,能将复杂抽象的几何概念具象化,让学生更容易理解,能培养学生的语言转化能力和空间想象能力,为学生的学习奠定基础。因此,教师要不断优化模型教学的应用方式,提高教学效率和教学质量,提升学生的数学核心素养。
四、总结
感谢聆听
核心素养下的几何模型教学策略
(九年级数学)
一、数学核心素养
会用数学的眼光观察现实世界
抽象能力、几何直观、
空间观念、创新意识
一、数学核心素养
会用数学的思维思考现实世界
运算能力、推理能力
一、数学核心素养
会用数学的语言表达现实世界
数据意识、模型意识、应用意识
二、相似三角形模型
1.平行线分线段成比例模型
我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系:
这就是如下的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.(简称:平行线分线段成比例)
【模型证明】
连接AE、DF、DC、BF
作出下图点A关于线段BC的对称点
A’
【2023长春市模22题】
当图中的点A、F重合时,就形成了一个三角形的特殊情形.
当图中的直线m、n相交于第二条直线上某点时,也构成了一种特殊情形.
2. A、X模型
A型
X型
已知:DE∥BC
结论:△ADE∽△ABC
在相似三角形的判定中,我们常通过作平行线、从而得出A型或X型相似.
【模型证明】
过D作DF∥AC,交BC于点F
【模型证明】
过E作EF∥BC,交CB延长线于点F
已知:
求:BE的长(用含a、b、m、n的式子表示)
令
【模型拓展:梯形中位线证明】
【模型拓展:倒数模型】
【模型拓展:角平分线分线段成比例】
【模型拓展:角平分线分线段成比例】
过点C作AD的平行线,与BA延长线交于点E
【模型拓展:角平分线分线段成比例】
15°的各个三角函数值也可以利用此方法计算
【模型拓展:12345模型】
【模型拓展:12345模型】
以15°为例,简单介绍一下计算方法
【模型拓展:梅氏定理】
【模型拓展:梅氏定理】
过D作DH∥CF交AB于点H
【模型拓展:重心模型】
在△ABC中,D、E、分别是BC、AC中点,连结AD、
BE交于点F,证明:
【模型拓展】证明三角形三条中线交于一点
【模型拓展】
模型结论:
3. 反A、X模型
模型结论:
黄金三角形
顶角为36°的等腰三角形,底边与腰长的比∠C的平分线,交AB于D,D为AB的黄金分割点。
模型结论:
模型结论:
反“X”模型
条件:∠A=∠C
【模型拓展:托勒密定理】
【与圆有关的相似】
相交弦定理
割线定理
切割线定理
4. 一线三等角模型
模型结论:
【锐角型】
如图,等腰△ABC,∠DEF=∠B=∠C
【模型证明】
4. 一线三等角模型
模型结论:
【钝角型】
如图,四边形ABCD中,∠DEC=∠A=∠B
【模型证明】
4. 一线三等角模型
【直角型】
如图,A、B、C三点共线,∠A=∠C=∠DBE=90°,用同样的方法,易证△ABD∽△CEB,直角型的一线三等角我们又叫做“三垂直模型”,它的应用更加广泛,考试出现概率最大
4. 一线三等角模型
同样可以证明两个三角形相似
正方形ABCD边长为5,点P、Q分别在直线CB、DC上(点P不与点C、B重合),且保持∠APQ=90°.当CQ=1时,求线段BP的长.
针对点P在直线CB上的位置进行分类讨论
点P在线段BC上
点P在线段CB延长线上
点P在线段BC延长线上
【模型应用】
5. 旋转相似模型
如图,已知DE∥BC,将△ADE绕点A旋转一定角度,连接BD、CE.
旋转△ADE
△ADE∽△ABC
△ABD∽△ACE
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
【模型应用】直接应用旋转相似
【模型应用】构造旋转相似模型
如图,在△ABC中,∠BAC=2∠DBC=60°,D为△ABC内一点,连接DA、DB、DC,若∠BDC=90°, ,AC=6,则AB的长为?
将△ADC绕点D顺时针旋转90°,并放大 倍.
【模型应用】构造旋转相似模型
如图,在△ABC中,∠BAC=2∠DBC=60°,D为△ABC内一点,连接DA、DB、DC,若∠BDC=90°, ,AC=6,则AB的长为?
将△ADC绕点C顺时针旋转90°,并放大2倍.
【模型拓展】瓜豆模型
△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当点P在直线l上运动时,Q的轨迹是?
【模型拓展】瓜豆模型
△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当点P在圆O上运动时,Q的轨迹是?
三、圆的相关模型
1.连半径构造等腰三角形模型
已知AB是圆O的一条弦,连结OA、OB,则∠A=∠B.
在圆的相关题目中,不要忽略隐含的已知条件,我们通常可以连结半径构造等腰三角形,利用等腰三角形的性质及圆中的相关定理,解决角度的计算问题.
如图,AB是圆O的直径,弦PQ交AB于M,且PM=MO.求证:
如图,连接OP、OQ
∵PM=OM,
∴∠P=∠MOP.
∵OP=OQ,
∴∠P=∠Q.
∵∠QMO=2∠MOP,
∴∠BOQ=3∠MOP.
∴∠AOP=∠BOQ.
∴
2.构造直角三角形模型
当图形中含有直径时,构造直径所对的圆周角是解决问题的重要思路,在证明有关问题中注意90°圆周角的构造.
在解决求弦长,弦心距,半径问题时,在圆中常作弦心距或连接半径作为辅助线,利用弦心距、半径和半弦组成一个直角三角形,再利用勾股定理进行计算
如图,AB是圆O的直径,AB=AC,BC交圆O于点D,AC交圆O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
(1)
(2)
连接AD
已知圆O的直径AB和弦CD相交于点E,AE=2,BE=6,∠DEB=60°.求CD的长
过点O作OF⊥CD于点F,连接OD.
3.与圆的切线有关的辅助线
(1)已知切线:连接过切点的半径.如图,已知直线AB是圆O的切线,点C是切点.连接OC,则OC⊥AB.
(2)证明切线:
①当已知直线经过圆上的一点时,连半径,证垂直.
②如果不知道直线与圆是否有交点时,作垂直,证明 垂线段长度等于半径.
如图,OA、OB是圆O的半径,且OA⊥OB,P是OA上任意一点,BP的延长线交圆O于点Q,过Q点的切线交OA延长线于R点.求证:RP=RQ.
如图,连接OQ.
∵OQ=OB,
∴∠OQB=∠OBQ.
∵RQ为圆O的切线,OA⊥OB,
∴∠BPO=90°-∠OBQ,∠BQR=90°-∠OQB.
∴∠BPO=∠QPR=∠BQR.
∴RP=RQ
如图,△ABC内接于圆O,过点A作直线DE,当∠BAE=∠C时,试确定直线DE与圆O的位置关系,并证明你的结论.
直线DE与圆O相切,理由如下:
如图,连接AO并延长,交圆O于点F,连接BF.
∵∠BAE=∠C,∠C=∠F,
∴∠BAE=∠F.
∵AF为直径,
∴∠ABF=90°.
∴∠F+∠BAF=90°.
∴∠BAE+∠BAF=90°.
∴FA⊥DE.
∵AO是圆O的半径,
∴直线DE与圆O相切.
如图,AB是圆O的直径,AC是它的切线,CO平分∠ACD.求证:CD是圆O的切线.
如图,过点O作OE⊥CD于点E.
∵AC是圆O的切线,
∴OA⊥AC.
∵CO平分∠ACD,OE⊥CD,
∴OA=OE.
∴CD是圆O的切线.
辅助圆模型
【模型一】共端点,等线段模型
图①
图②
图③
如图①,出现“共端点,等线段”时,可利用圆的定义构造辅助圆.
如图②,若OA=OB=OC,则A、B、C三点在以O为圆心,OA为半径的圆上.
如图③,∠ACB=1/2∠AOB,∠BAC=1/2∠BOC.
如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD.
求证:∠1+∠2=90°.
∵AB=AC=AD,
∴B、C、D在以A为圆心,AB为半径的圆A上.
∴∠BAC=2∠1.
∵AB=AC,
∴∠ABC=∠2.
在△ABC中,
∵∠BAC+∠ABC+∠2=180°,
∴2∠1+2∠2=180°.
∴∠1+∠2=90°.
辅助圆模型
【模型二】直角三角形共斜边模型
(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆.
(2)四点共圆后,可以根据圆周角定理得到角度相等,完成角度等量关系转化,是证明角度相等的重要途径之一。
如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外角平分线于点F,求证:FE=DE.
连接DB、DF.
∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,
∴∠CBF=45°,∠DBC=45°,
∴∠DBF=90°.
又∵∠DEF=90°,
∴D、E、B、F四点共圆.
∴∠DFE=∠DBE=45°.
∴△DEF是等腰直角三角形.
∴FE=DE.
如图,BE、CF为△ABC的高,且交于点H,连接AH并延长交BC于点D.求证:AD⊥BC.
【模型拓展】三角形三条高线交于一点
连接EF.
∵Rt△AFH和Rt△AEH共斜边AH,
∴A、F、H、E四点共圆.
∴∠1=∠2.
∵Rt△BCF和Rt△BEC共斜边BC,
∴F、B、C、E四点共圆.
∴∠1=∠3.
∴∠2=∠3
∵∠3+∠ABD=90°,
∴∠2+∠ABD=90°
∴AD⊥BC.
总之,几何是数学教学的重要组成部分,也是数学教学的难点。在几何教学中采用模型教学具有重要意义,能将复杂抽象的几何概念具象化,让学生更容易理解,能培养学生的语言转化能力和空间想象能力,为学生的学习奠定基础。因此,教师要不断优化模型教学的应用方式,提高教学效率和教学质量,提升学生的数学核心素养。
四、总结
感谢聆听
