1.1直线的斜率和倾斜角 课件(共21张PPT)
文档属性
| 名称 | 1.1直线的斜率和倾斜角 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 11:09:13 | ||
图片预览





文档简介
(共21张PPT)
直线的斜率与倾斜角
1.1
苏教版(2019)选择性必修一
第一章 直线与方程
一、知识梳理
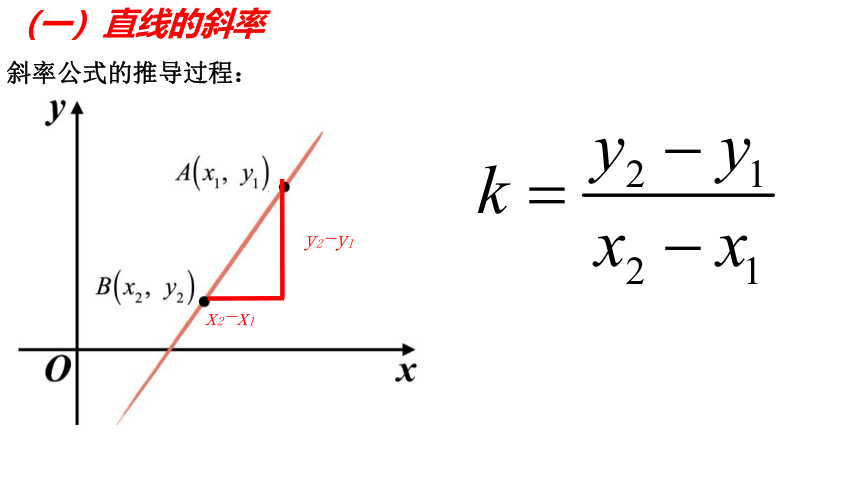
(一)直线的斜率
斜率公式:
【注意】利用斜率公式计算直线的斜率时,两点坐标顺序不影响结果。
(一)直线的斜率
斜率公式的推导过程:
y2-y1
x2-x1
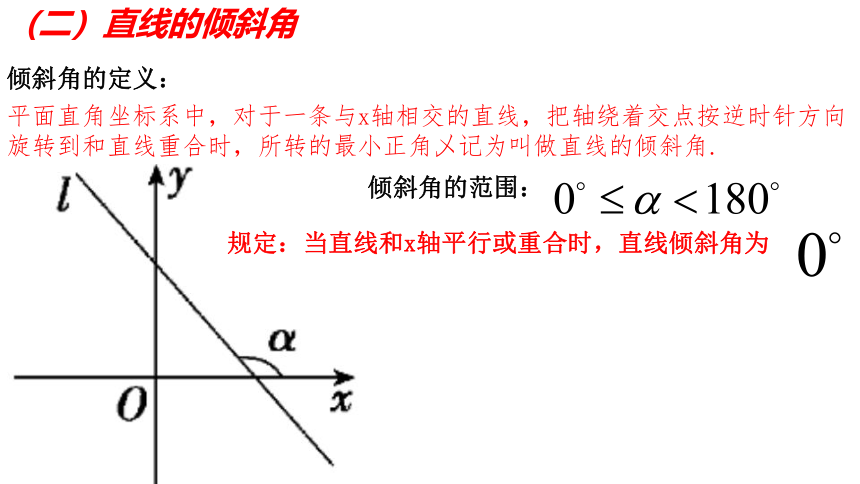
(二)直线的倾斜角
倾斜角的定义:
平面直角坐标系中,对于一条与x轴相交的直线,把轴绕着交点按逆时针方向旋转到和直线重合时,所转的最小正角乄记为叫做直线的倾斜角.
倾斜角的范围:
规定:当直线和x轴平行或重合时,直线倾斜角为
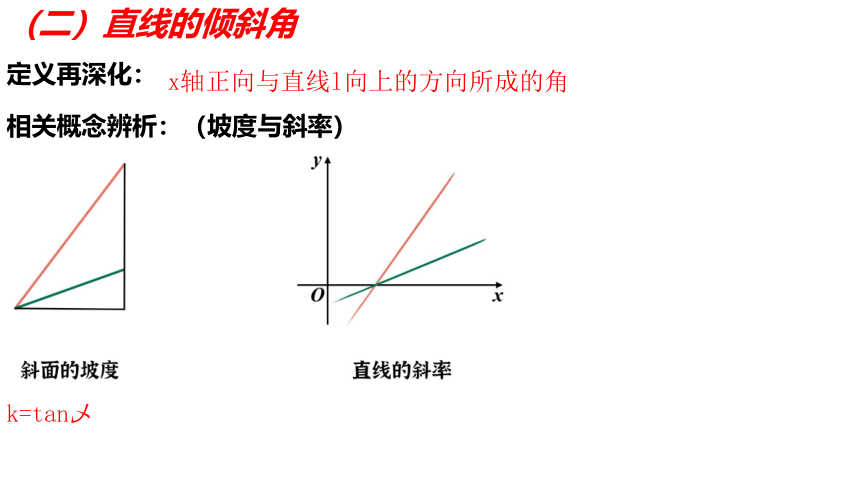
(二)直线的倾斜角
定义再深化:
x轴正向与直线l向上的方向所成的角
相关概念辨析:(坡度与斜率)
k=tan乄
(三)直线的倾斜角与斜率的关系
图示
倾斜角(范围)
斜率(范围)
不存在
每条直线都有倾斜角
但不是每条直线都有斜率
二、题型归纳
三、对点练习
判断:
斜率相等的两直线倾斜角一定相等
×
拓展:
两直线垂直与平行的判定
平行:k1=k2
垂直:k1 k2=-1
题型一 根据两点坐标求直线斜率
【例1】(2023春·河北张家口·高二张家口市宣化第一中学校考阶段练习)
经过点(-3,1)和点(4,-2)的直线l的斜率是 .
【变式1-1】(2022秋·重庆北碚·高二重庆市兼善中学校考阶段练习)
过两点(a+1,a-1)和(a,a)的直线的斜率为( )
A.a B.1 C.-a D.-1
D
题型二 斜率与倾斜角的关系应用
【例2】(2022秋·河南郑州·高二郑州外国语学校校考阶段练习)
下列说法正确的是( )
A.若直线的斜率为tan乄,则该直线的倾斜角为乄
B.直线的倾斜角乄的取值范围是
C.平面直角坐标系中的任意一条直线都有斜率
D.直线的倾斜角越大,其斜率就越大
B
【变式2-1】(2022秋·广西玉林·高二校考阶段练习)下列命题正确的是( )
①直线倾斜角的范围是[0°,180°);②若直线的斜率为k,则k∈R;③任何一条直线都有斜率,但不一定有倾斜角;④任何一条直线都有倾斜角,但不一定有斜率.
A.①② B.①④ C.①②④ D.①②③
C
【变式2-2】(2022秋·安徽六安·高二校考阶段练习)
将直线MN绕原点旋60°转得到直线M'N',若直线M'N'的斜率为1,则直线MN的倾斜角是( )
A.105°
B.165°
C.15°或75°
D.105°或165°
D
题型三 图象中的斜率与倾斜角
【例3】(2022秋·河北石家庄·高二校考阶段练习)
如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
D
A.
B.
C.
D.
【变式3-1】(2022·全国·高二专题练习)
如图,直线l1,l2,l3,l4的斜率分别为k1,k2,k3,k4,则( )
A.
B.
C.
D.
D
题型四 利用斜率解决三点共线问题
【例4】(2022秋·安徽六安·高二校考阶段练习)已知点A(0,-8),B(2,-2),C(4,m),若线段AB,AC,BC不能构成三角形,则的值是 .
4
【变式4-1】(2022秋·浙江宁波·高二余姚中学校考阶段练习)已知三点A(2,-3)B(4,3)C(5,k)三点共线,则实数k的值为 .
6
题型五 直线与线段有公共点问题
【例5】(2022秋·北京·高二人大附中校考阶段练习)已知点A(1,-2)和点B(2,1),经过点P(0,-1)作直线l,若直线l与射线AB有公共点,则直线l的斜率的取值范围是( )
A.[-1.3] B.(-∞,-1]U(3,+∞)
C.[-1.1] D.(-∞,-1]U[1,+∞)
A
【变式5-1】(2022秋·安徽芜湖·高二安徽省无为襄安中学校考阶段练习)
经过点P(0,1)作直线l,若直线l与A(2,3),B(1,-2)连接,的线段总有公共点,则直线的斜率l的取值范围是 .
或
再见
感谢聆听
直线的斜率与倾斜角
1.1
苏教版(2019)选择性必修一
第一章 直线与方程
一、知识梳理
(一)直线的斜率
斜率公式:
【注意】利用斜率公式计算直线的斜率时,两点坐标顺序不影响结果。
(一)直线的斜率
斜率公式的推导过程:
y2-y1
x2-x1
(二)直线的倾斜角
倾斜角的定义:
平面直角坐标系中,对于一条与x轴相交的直线,把轴绕着交点按逆时针方向旋转到和直线重合时,所转的最小正角乄记为叫做直线的倾斜角.
倾斜角的范围:
规定:当直线和x轴平行或重合时,直线倾斜角为
(二)直线的倾斜角
定义再深化:
x轴正向与直线l向上的方向所成的角
相关概念辨析:(坡度与斜率)
k=tan乄
(三)直线的倾斜角与斜率的关系
图示
倾斜角(范围)
斜率(范围)
不存在
每条直线都有倾斜角
但不是每条直线都有斜率
二、题型归纳
三、对点练习
判断:
斜率相等的两直线倾斜角一定相等
×
拓展:
两直线垂直与平行的判定
平行:k1=k2
垂直:k1 k2=-1
题型一 根据两点坐标求直线斜率
【例1】(2023春·河北张家口·高二张家口市宣化第一中学校考阶段练习)
经过点(-3,1)和点(4,-2)的直线l的斜率是 .
【变式1-1】(2022秋·重庆北碚·高二重庆市兼善中学校考阶段练习)
过两点(a+1,a-1)和(a,a)的直线的斜率为( )
A.a B.1 C.-a D.-1
D
题型二 斜率与倾斜角的关系应用
【例2】(2022秋·河南郑州·高二郑州外国语学校校考阶段练习)
下列说法正确的是( )
A.若直线的斜率为tan乄,则该直线的倾斜角为乄
B.直线的倾斜角乄的取值范围是
C.平面直角坐标系中的任意一条直线都有斜率
D.直线的倾斜角越大,其斜率就越大
B
【变式2-1】(2022秋·广西玉林·高二校考阶段练习)下列命题正确的是( )
①直线倾斜角的范围是[0°,180°);②若直线的斜率为k,则k∈R;③任何一条直线都有斜率,但不一定有倾斜角;④任何一条直线都有倾斜角,但不一定有斜率.
A.①② B.①④ C.①②④ D.①②③
C
【变式2-2】(2022秋·安徽六安·高二校考阶段练习)
将直线MN绕原点旋60°转得到直线M'N',若直线M'N'的斜率为1,则直线MN的倾斜角是( )
A.105°
B.165°
C.15°或75°
D.105°或165°
D
题型三 图象中的斜率与倾斜角
【例3】(2022秋·河北石家庄·高二校考阶段练习)
如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
D
A.
B.
C.
D.
【变式3-1】(2022·全国·高二专题练习)
如图,直线l1,l2,l3,l4的斜率分别为k1,k2,k3,k4,则( )
A.
B.
C.
D.
D
题型四 利用斜率解决三点共线问题
【例4】(2022秋·安徽六安·高二校考阶段练习)已知点A(0,-8),B(2,-2),C(4,m),若线段AB,AC,BC不能构成三角形,则的值是 .
4
【变式4-1】(2022秋·浙江宁波·高二余姚中学校考阶段练习)已知三点A(2,-3)B(4,3)C(5,k)三点共线,则实数k的值为 .
6
题型五 直线与线段有公共点问题
【例5】(2022秋·北京·高二人大附中校考阶段练习)已知点A(1,-2)和点B(2,1),经过点P(0,-1)作直线l,若直线l与射线AB有公共点,则直线l的斜率的取值范围是( )
A.[-1.3] B.(-∞,-1]U(3,+∞)
C.[-1.1] D.(-∞,-1]U[1,+∞)
A
【变式5-1】(2022秋·安徽芜湖·高二安徽省无为襄安中学校考阶段练习)
经过点P(0,1)作直线l,若直线l与A(2,3),B(1,-2)连接,的线段总有公共点,则直线的斜率l的取值范围是 .
或
再见
感谢聆听
