北师大版数学七年级上册 第二章第1课时 有理数乘方的意义导学案(表格式 无答案)
文档属性
| 名称 | 北师大版数学七年级上册 第二章第1课时 有理数乘方的意义导学案(表格式 无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 27.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 00:00:00 | ||
图片预览

文档简介
9 有理数的乘方
第1课时 有理数乘方的意义
课题 第一课时 有理数乘方的意义
学习目标 1.理解有理数乘方的意义,掌握幂、底数、指数的概念. 2.能进行有理数的乘方运算. 3.培养学生观察、类比、归纳能力.渗透分类讨论思想,增强团体意识.
学习策略 理解概念,掌握形式,主动探索
学习过程 复习巩固 1.平方和立方:=___表示:___个___相乘。=___表示的意义:___个___相乘。 2.有理数乘法法则:两数相乘,同号得 ,异号得 ,绝对值相乘。任何数与0相乘,积为 。几个不为0的数相乘,当负因数有奇数个时,积为 ;当负因数有偶数个时,积为 。
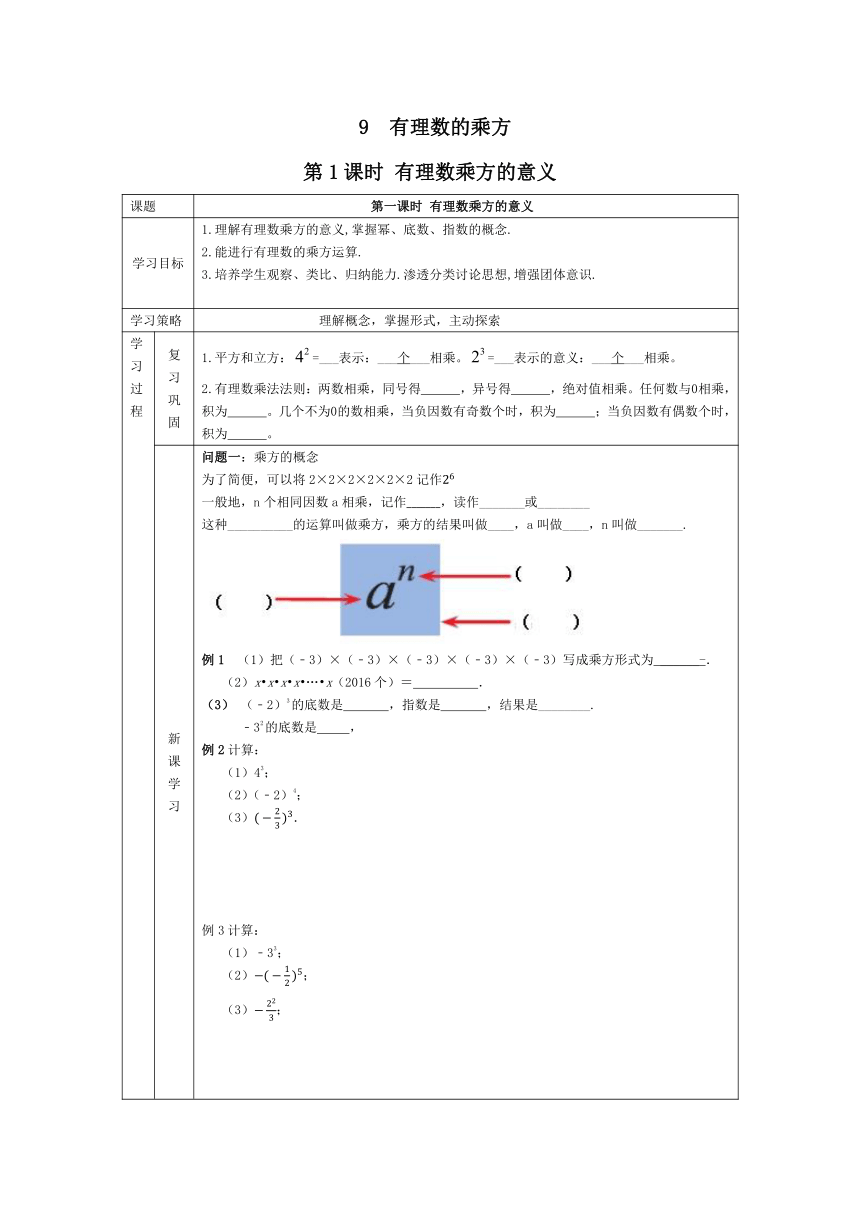
新课学习 问题一:乘方的概念 为了简便,可以将2×2×2×2×2×2记作 一般地,n个相同因数a相乘,记作,读作_______或________ 这种__________的运算叫做乘方,乘方的结果叫做____,a叫做____,n叫做_______. 例1 (1)把(﹣3)×(﹣3)×(﹣3)×(﹣3)×(﹣3)写成乘方形式为 ______-. (2)x x x x … x(2016个)= . (3) (﹣2)3的底数是 ,指数是 ,结果是________. ﹣32的底数是 , 例2计算: (1)43; (2)(﹣2)4; (3). 例3计算: (1)﹣33; (2); (3);
尝试应用 1.(2021 温州中考)计算(﹣2)2的结果是( ) A.4 B.﹣4 C.1 D.﹣1 2.下列各组数中,相等的是( ) A.﹣33和(﹣3)3 B.﹣42和(﹣4)2 C.43和34 D.和 3.在有理数中,一个数的立方等于这个数本身,这种数的个数为( ) A.1 B.2 C.3 D.无数个 4.35表示的意义是 .8个相乘用幂的形式简写成 . 5.(﹣4)2的底数是 ,指数是 ,结果是 . 6.平方等于49的数为 . 7.计算: (1)(﹣6)3 (2)﹣63 (3)()4 (4).
达标测试 1.计算(﹣2)2结果为( ) A.﹣4 B.±4 C.4 D.±2 2.﹣43表示( ) A.3个﹣4相乘 B.3个4相乘的相反数 C.4个﹣3相乘 D.4个3相乘的相反数 3.下列各组数中,相等的一组是( ) A.﹣(﹣1)与﹣|﹣1| B.﹣32与(﹣3)2 C.(﹣2)3与﹣23 D.与()2 4.平方等于它本身的数是( ) A.0 B.1 C.﹣1 D.0或1 5.()3的底数是 ,指数是 ,运算后的结果是 . 6.池塘里浮萍面积每天长大一倍,若经过12天长满整个池塘,问需 天浮萍长满半个池塘. 7.计算: (1);(2); (3)﹣25;(4). 8.请认真阅读下面材料,并解答下列问题. 如果a(a>0,a≠1)的b次幂等于N,即指数式ab=N,那么数b叫做以a为底N的对数,对数式记作:logaN=b.例如: ①因为指数式22=4,所以以2为底4的对数是2,对数式记作:log24=2; ②因为指数式42=16,所以以4为底16的对数是2,对数式记作:log416=2. (1)请根据上面阅读材料将下列指数式改为对数式: ①62=36; ②43=64; (2)将下列对数式改为指数式: ①log525=2; ②log327=3; (3)计算:log232.
第1课时 有理数乘方的意义
课题 第一课时 有理数乘方的意义
学习目标 1.理解有理数乘方的意义,掌握幂、底数、指数的概念. 2.能进行有理数的乘方运算. 3.培养学生观察、类比、归纳能力.渗透分类讨论思想,增强团体意识.
学习策略 理解概念,掌握形式,主动探索
学习过程 复习巩固 1.平方和立方:=___表示:___个___相乘。=___表示的意义:___个___相乘。 2.有理数乘法法则:两数相乘,同号得 ,异号得 ,绝对值相乘。任何数与0相乘,积为 。几个不为0的数相乘,当负因数有奇数个时,积为 ;当负因数有偶数个时,积为 。
新课学习 问题一:乘方的概念 为了简便,可以将2×2×2×2×2×2记作 一般地,n个相同因数a相乘,记作,读作_______或________ 这种__________的运算叫做乘方,乘方的结果叫做____,a叫做____,n叫做_______. 例1 (1)把(﹣3)×(﹣3)×(﹣3)×(﹣3)×(﹣3)写成乘方形式为 ______-. (2)x x x x … x(2016个)= . (3) (﹣2)3的底数是 ,指数是 ,结果是________. ﹣32的底数是 , 例2计算: (1)43; (2)(﹣2)4; (3). 例3计算: (1)﹣33; (2); (3);
尝试应用 1.(2021 温州中考)计算(﹣2)2的结果是( ) A.4 B.﹣4 C.1 D.﹣1 2.下列各组数中,相等的是( ) A.﹣33和(﹣3)3 B.﹣42和(﹣4)2 C.43和34 D.和 3.在有理数中,一个数的立方等于这个数本身,这种数的个数为( ) A.1 B.2 C.3 D.无数个 4.35表示的意义是 .8个相乘用幂的形式简写成 . 5.(﹣4)2的底数是 ,指数是 ,结果是 . 6.平方等于49的数为 . 7.计算: (1)(﹣6)3 (2)﹣63 (3)()4 (4).
达标测试 1.计算(﹣2)2结果为( ) A.﹣4 B.±4 C.4 D.±2 2.﹣43表示( ) A.3个﹣4相乘 B.3个4相乘的相反数 C.4个﹣3相乘 D.4个3相乘的相反数 3.下列各组数中,相等的一组是( ) A.﹣(﹣1)与﹣|﹣1| B.﹣32与(﹣3)2 C.(﹣2)3与﹣23 D.与()2 4.平方等于它本身的数是( ) A.0 B.1 C.﹣1 D.0或1 5.()3的底数是 ,指数是 ,运算后的结果是 . 6.池塘里浮萍面积每天长大一倍,若经过12天长满整个池塘,问需 天浮萍长满半个池塘. 7.计算: (1);(2); (3)﹣25;(4). 8.请认真阅读下面材料,并解答下列问题. 如果a(a>0,a≠1)的b次幂等于N,即指数式ab=N,那么数b叫做以a为底N的对数,对数式记作:logaN=b.例如: ①因为指数式22=4,所以以2为底4的对数是2,对数式记作:log24=2; ②因为指数式42=16,所以以4为底16的对数是2,对数式记作:log416=2. (1)请根据上面阅读材料将下列指数式改为对数式: ①62=36; ②43=64; (2)将下列对数式改为指数式: ①log525=2; ②log327=3; (3)计算:log232.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
