2014年秋人教版八年级数学上册:11.2《与三角形有关的角》
文档属性
| 名称 | 2014年秋人教版八年级数学上册:11.2《与三角形有关的角》 |  | |
| 格式 | zip | ||
| 文件大小 | 46.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 14:03:59 | ||
图片预览



文档简介
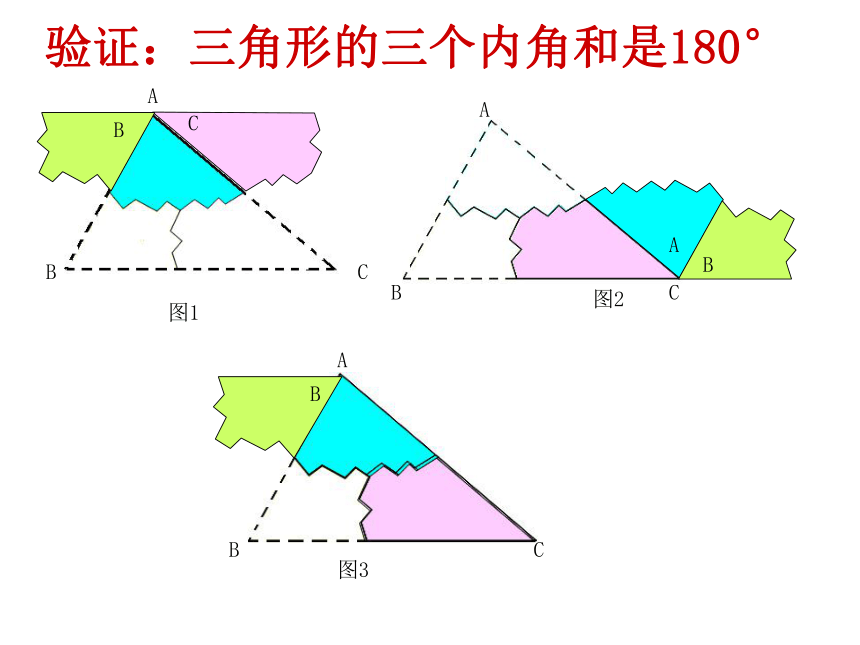
课件17张PPT。11.2 与三角形有关的角旧知回顾我们已经知道,任意一个三角形的内角和等于180°.怎么证明这个结论呢?方法一:通过具体的度量,验证三角形的内角和为180°.验证:三角形的三个内角和是180°图1图2 图3ABCAABBCC
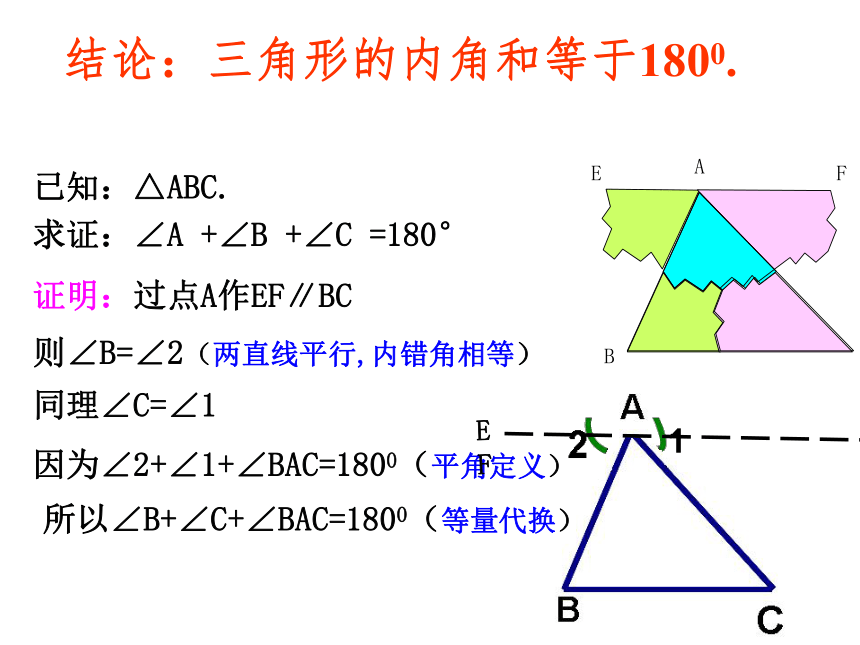
结论:三角形的内角和等于1800.证明:过点A作EF∥BC则∠B=∠2(两直线平行,内错角相等)
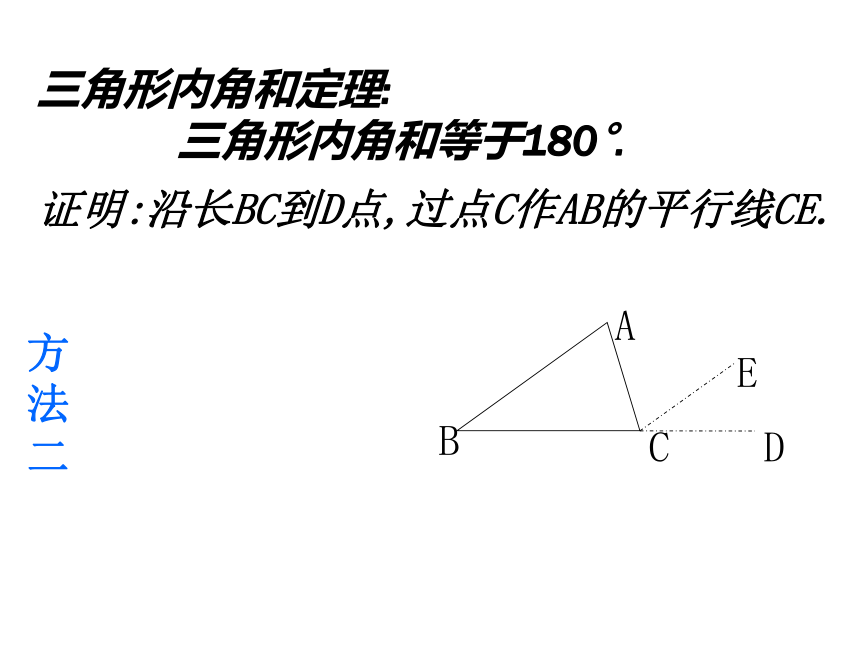
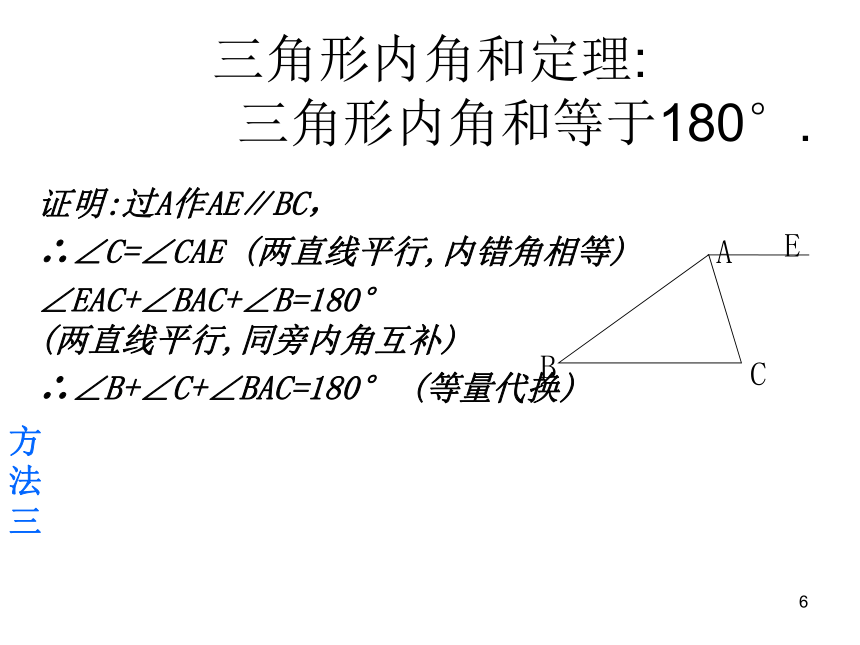
同理∠C=∠1因为∠2+∠1+∠BAC=1800(平角定义) 所以∠B+∠C+∠BAC=1800(等量代换)已知:△ABC.求证:∠A +∠B +∠C =180°E F三角形内角和定理: 三角形内角和等于180°.证明:沿长BC到D点,过点C作AB的平行线CE.方法二证明:过A作AE∥BC,
∴∠C=∠CAE (两直线平行,内错角相等)
∠EAC+∠BAC+∠B=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180° (等量代换)方法三三角形内角和定理: 三角形内角和等于180°.三角形内角和定理: 三角形内角和等于180°.证明:过⊿ABC的两个锐角作BC的垂线BD和CE,
过点A作BD的平行线AF.由图可知BD∥AF∥CE.
∴∠BAF=∠ABD
∠ECA=∠FAC
(两条直线平行,内错角相等.)
∴ ⊿ABC的三个内角
∠A+∠B+∠C=∠ABC+∠ACB+ ∠BAF+ ∠FAC=
=∠DBA+∠ABC+∠ACB+∠ACE=90°+90°=180°方法四思路总结为了证明三个角的和为180°,利用逆向思考的方法,把问题转化为一个平角,同旁内角互补,或者两个直角之和,或者其它方法.这种转化思想是数学中的常用方法.一个三角形中能有两个直角吗?
一个三角形中能有两个钝角吗?
三个内角都能小于600吗?
讨论例题讲解 例1.已知: 在△ ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数。例题讲解 例2.如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?练一练 1.求出下列图中x的值: xx x x =600x x x =4502 x x┐x =300练一练2.在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=50°
练一练 3.已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x.
列出方程 x+3x+5x=180°
x=20°
答:三个内角度数分别为20°,60°,100°。练一练证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜(等量代换)
∴∠A+∠B=180゜-90゜= 90゜
(等式性质)
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且发现要证明三角形三个内角的和等于180 °需
转化为:平角或两直线平行同旁内角和等于180°。作 业 这节课我们学习到这里,再见!
结论:三角形的内角和等于1800.证明:过点A作EF∥BC则∠B=∠2(两直线平行,内错角相等)
同理∠C=∠1因为∠2+∠1+∠BAC=1800(平角定义) 所以∠B+∠C+∠BAC=1800(等量代换)已知:△ABC.求证:∠A +∠B +∠C =180°E F三角形内角和定理: 三角形内角和等于180°.证明:沿长BC到D点,过点C作AB的平行线CE.方法二证明:过A作AE∥BC,
∴∠C=∠CAE (两直线平行,内错角相等)
∠EAC+∠BAC+∠B=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180° (等量代换)方法三三角形内角和定理: 三角形内角和等于180°.三角形内角和定理: 三角形内角和等于180°.证明:过⊿ABC的两个锐角作BC的垂线BD和CE,
过点A作BD的平行线AF.由图可知BD∥AF∥CE.
∴∠BAF=∠ABD
∠ECA=∠FAC
(两条直线平行,内错角相等.)
∴ ⊿ABC的三个内角
∠A+∠B+∠C=∠ABC+∠ACB+ ∠BAF+ ∠FAC=
=∠DBA+∠ABC+∠ACB+∠ACE=90°+90°=180°方法四思路总结为了证明三个角的和为180°,利用逆向思考的方法,把问题转化为一个平角,同旁内角互补,或者两个直角之和,或者其它方法.这种转化思想是数学中的常用方法.一个三角形中能有两个直角吗?
一个三角形中能有两个钝角吗?
三个内角都能小于600吗?
讨论例题讲解 例1.已知: 在△ ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数。例题讲解 例2.如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?练一练 1.求出下列图中x的值: xx x x =600x x x =4502 x x┐x =300练一练2.在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=50°
练一练 3.已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x.
列出方程 x+3x+5x=180°
x=20°
答:三个内角度数分别为20°,60°,100°。练一练证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜(等量代换)
∴∠A+∠B=180゜-90゜= 90゜
(等式性质)
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且发现要证明三角形三个内角的和等于180 °需
转化为:平角或两直线平行同旁内角和等于180°。作 业 这节课我们学习到这里,再见!
