14.2.2三角形全等判定(ASA)课件
文档属性
| 名称 | 14.2.2三角形全等判定(ASA)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 191.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-04 17:53:58 | ||
图片预览

文档简介
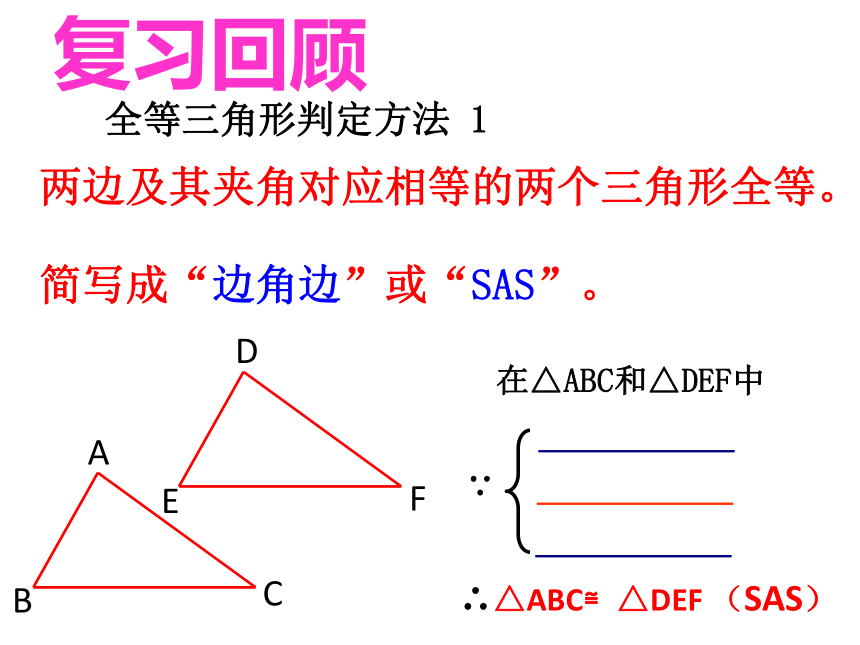
课件14张PPT。沪科版八年级(上册)14.2 全等三角形的判定(第二课时)安庆市白泽湖中学 郑玉兵 全等三角形判定方法 1∴△ABC≌△DEF (SAS)复习回顾两边及其夹角对应相等的两个三角形全等。
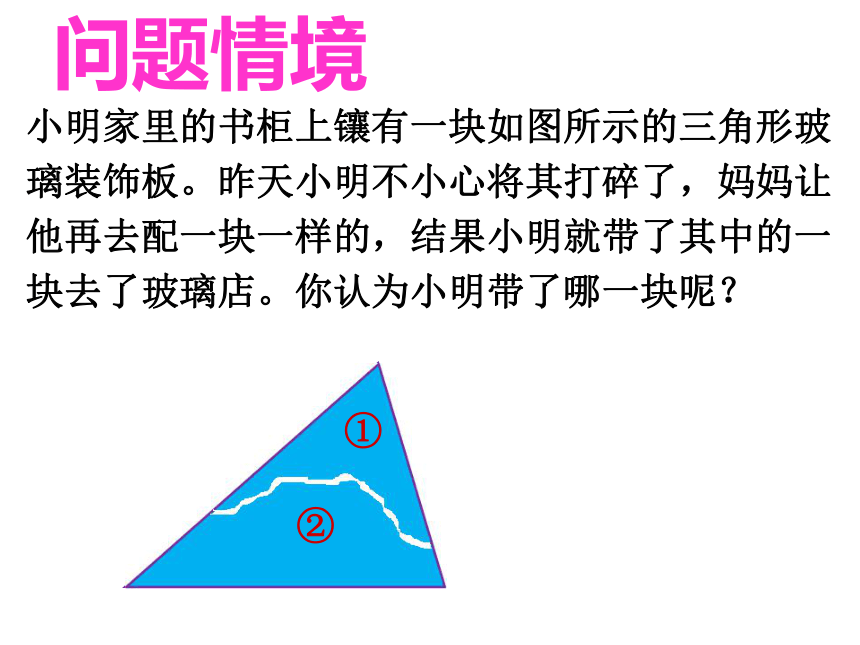
简写成“边角边”或“SAS”。小明家里的书柜上镶有一块如图所示的三角形玻
璃装饰板。昨天小明不小心将其打碎了,妈妈让
他再去配一块一样的,结果小明就带了其中的一
块去了玻璃店。你认为小明带了哪一块呢?
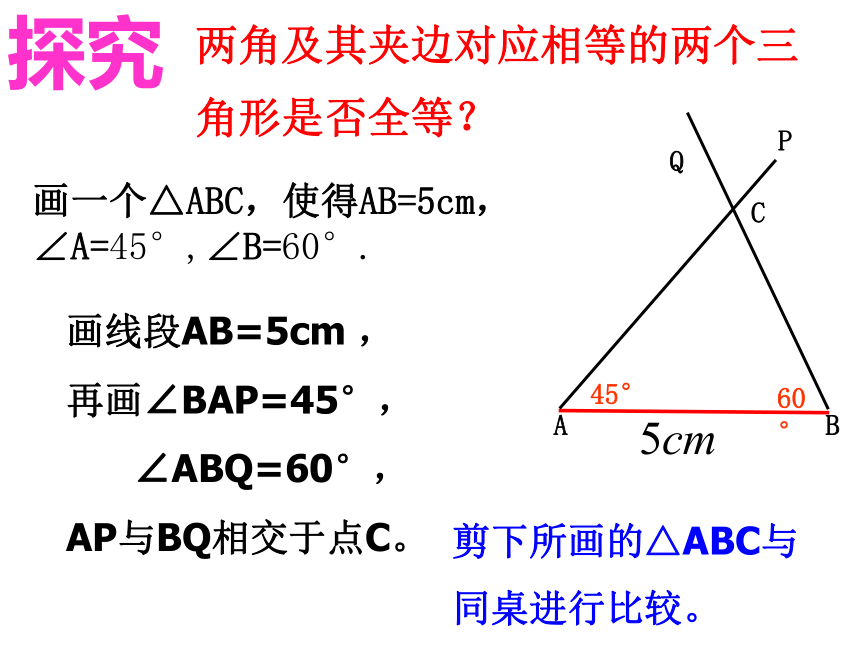
①②问题情境画线段AB=5cm ,
再画∠BAP=45°,
∠ABQ=60°,
AP与BQ相交于点C。剪下所画的△ABC与
同桌进行比较。ABPQ
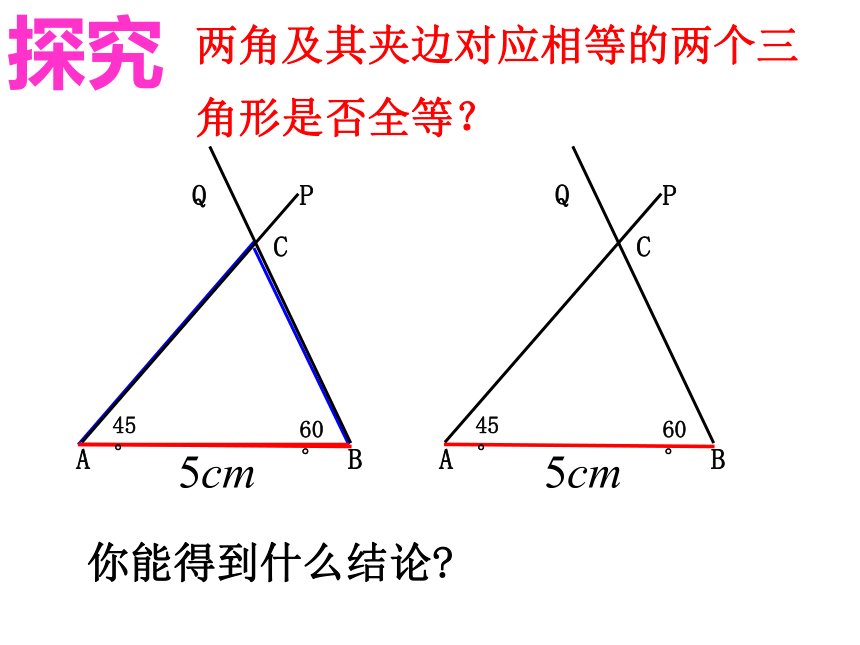
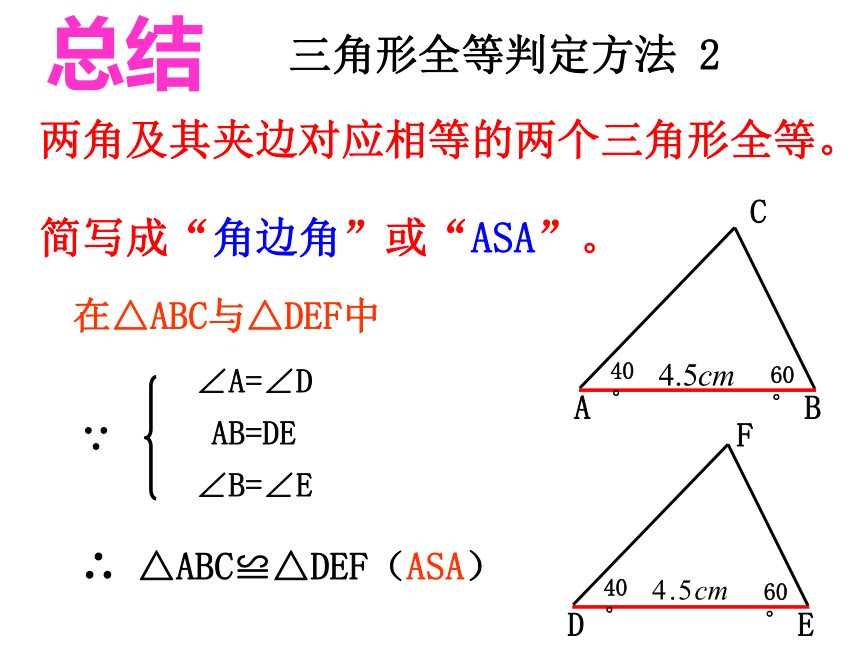
C45°60°探究两角及其夹边对应相等的两个三角形是否全等?画一个△ABC,使得AB=5cm,∠A=45°,∠B=60°.你能得到什么结论?探究两角及其夹边对应相等的两个三角形是否全等? 三角形全等判定方法 2在△ABC与△DEF中∴ △ABC≌△DEF(ASA)两角及其夹边对应相等的两个三角形全等。
简写成“角边角”或“ASA”。∠A=∠D
AB=DE
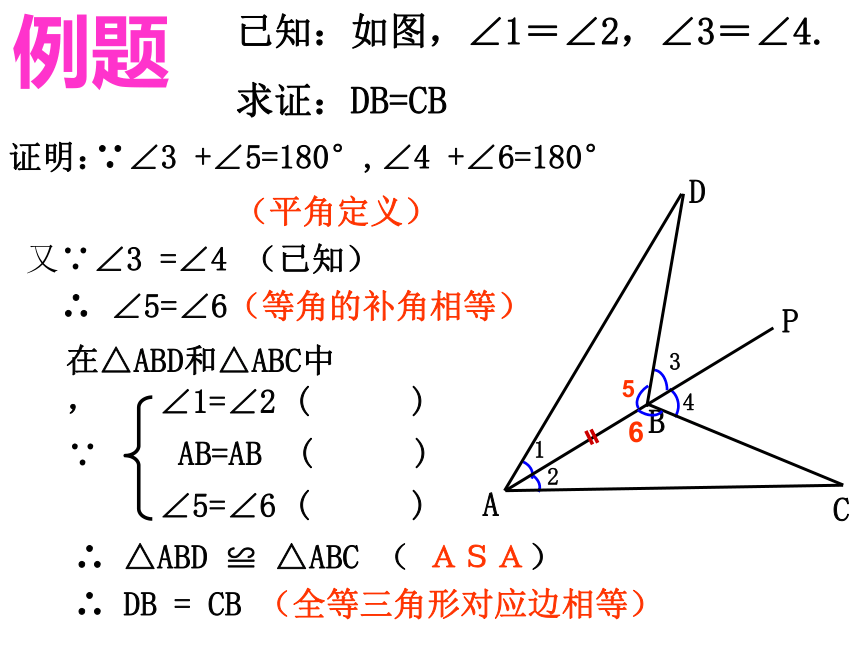
∠B=∠E∵ 总结 已知:如图,∠1=∠2,∠3=∠4.
求证:DB=CB 证明:∵∠3 +∠5=180°,∠4 +∠6=180°∴ ∠5=∠6(等角的补角相等)在△ABD和△ABC中,∴ △ABD ≌ △ABC ( ASA) 456(平角定义)又∵∠3 =∠4 (已知)∠1=∠2 ( )
AB=AB ( )
∠5=∠6 ( )∵∴ DB = CB (全等三角形对应边相等)例题练习:2、已知:如图,在△ABC中,
AD平分∠BAC,AD⊥BC于点D,
求证:∠B=∠C.121、已知:如图,∠1=∠2,
∠3=∠4,
求证:△ABC≌△BAD.证明:∠DAB=∠CBA (已证)AB = BA (公共边) ∴△ABC≌△BAD ( ASA ) 练习解答:1、已知:如图,∠1=∠2,∠3=∠4,
求证:△ABC≌△BAD.∵ ∠1=∠2,∠3=∠4(已知)即 ∠DAB = ∠CBA∠1 = ∠2 (已知)∴ ∠1+∠3=∠2+∠4(等式性质)练习:2、已知:如图,在△ABC中,
AD平分∠BAC,AD⊥BC与点D,
求证:∠B=∠C.1234∠3 = ∠4 (已证)AD = AD (公共边) ∴△ABD≌△ACD ( ASA )∵ AD平分∠BAC(已知)∠1 = ∠2 (已证)证明:∴∠1=∠2 (角平分线定义)∵ AD⊥BC(已知)∴∠3=∠4=90° (垂直定义)∴∠B =∠C
(全等三角形对应角相等)挑战:已知:如图,点A、B、C、D在同一条直线上,AB=CD,AE⊥AD于A,BF⊥AD于B,CE∥DF.
求证:AE=BF.12解答:已知:如图,A、B、C、D四点在同一条直线上,AB=CD,
AE⊥AD于A,BF⊥AD于B,CE∥DF.求证:AE=BF.∠2 = ∠D (已证)AC = BD (已证) ∴△ACE≌△BDF( ASA )∵ AE⊥AD,BF⊥AD(已知)∠A = ∠1 (已证)证明:∵ CE∥DF(已知)∴∠2=∠D (两直线---- )∴AE =BF
(全等三角形对应边相等)∴∠A=∠1=90°(垂直定义)∵ AB=CD (已知)∴ AB+BC=CD+BC(等式性质)即 AC=BD 2、在应用“ASA”时要注意:必须是对应的两角及两角所夹的边相等。1、角边角:两角和它们的夹边对应相等的两个三角形全等(ASA)。3、今后判定两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。本节课你有什么收获?作业同步练习P75~77
基础练习14.2(二)第1~9题作业要认真完成哟!
简写成“边角边”或“SAS”。小明家里的书柜上镶有一块如图所示的三角形玻
璃装饰板。昨天小明不小心将其打碎了,妈妈让
他再去配一块一样的,结果小明就带了其中的一
块去了玻璃店。你认为小明带了哪一块呢?
①②问题情境画线段AB=5cm ,
再画∠BAP=45°,
∠ABQ=60°,
AP与BQ相交于点C。剪下所画的△ABC与
同桌进行比较。ABPQ
C45°60°探究两角及其夹边对应相等的两个三角形是否全等?画一个△ABC,使得AB=5cm,∠A=45°,∠B=60°.你能得到什么结论?探究两角及其夹边对应相等的两个三角形是否全等? 三角形全等判定方法 2在△ABC与△DEF中∴ △ABC≌△DEF(ASA)两角及其夹边对应相等的两个三角形全等。
简写成“角边角”或“ASA”。∠A=∠D
AB=DE
∠B=∠E∵ 总结 已知:如图,∠1=∠2,∠3=∠4.
求证:DB=CB 证明:∵∠3 +∠5=180°,∠4 +∠6=180°∴ ∠5=∠6(等角的补角相等)在△ABD和△ABC中,∴ △ABD ≌ △ABC ( ASA) 456(平角定义)又∵∠3 =∠4 (已知)∠1=∠2 ( )
AB=AB ( )
∠5=∠6 ( )∵∴ DB = CB (全等三角形对应边相等)例题练习:2、已知:如图,在△ABC中,
AD平分∠BAC,AD⊥BC于点D,
求证:∠B=∠C.121、已知:如图,∠1=∠2,
∠3=∠4,
求证:△ABC≌△BAD.证明:∠DAB=∠CBA (已证)AB = BA (公共边) ∴△ABC≌△BAD ( ASA ) 练习解答:1、已知:如图,∠1=∠2,∠3=∠4,
求证:△ABC≌△BAD.∵ ∠1=∠2,∠3=∠4(已知)即 ∠DAB = ∠CBA∠1 = ∠2 (已知)∴ ∠1+∠3=∠2+∠4(等式性质)练习:2、已知:如图,在△ABC中,
AD平分∠BAC,AD⊥BC与点D,
求证:∠B=∠C.1234∠3 = ∠4 (已证)AD = AD (公共边) ∴△ABD≌△ACD ( ASA )∵ AD平分∠BAC(已知)∠1 = ∠2 (已证)证明:∴∠1=∠2 (角平分线定义)∵ AD⊥BC(已知)∴∠3=∠4=90° (垂直定义)∴∠B =∠C
(全等三角形对应角相等)挑战:已知:如图,点A、B、C、D在同一条直线上,AB=CD,AE⊥AD于A,BF⊥AD于B,CE∥DF.
求证:AE=BF.12解答:已知:如图,A、B、C、D四点在同一条直线上,AB=CD,
AE⊥AD于A,BF⊥AD于B,CE∥DF.求证:AE=BF.∠2 = ∠D (已证)AC = BD (已证) ∴△ACE≌△BDF( ASA )∵ AE⊥AD,BF⊥AD(已知)∠A = ∠1 (已证)证明:∵ CE∥DF(已知)∴∠2=∠D (两直线---- )∴AE =BF
(全等三角形对应边相等)∴∠A=∠1=90°(垂直定义)∵ AB=CD (已知)∴ AB+BC=CD+BC(等式性质)即 AC=BD 2、在应用“ASA”时要注意:必须是对应的两角及两角所夹的边相等。1、角边角:两角和它们的夹边对应相等的两个三角形全等(ASA)。3、今后判定两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。本节课你有什么收获?作业同步练习P75~77
基础练习14.2(二)第1~9题作业要认真完成哟!
