第14章 勾股定理 单元练习 2023-2024学年 华师大版八年级数学上册(含解析)
文档属性
| 名称 | 第14章 勾股定理 单元练习 2023-2024学年 华师大版八年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 791.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 15:24:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第14章 勾股定理 单元练习 2023-2024学年 华师大版八年级数学上册(含解析)
一、单选题
1.如图,以的三边为直角边分别向外作等腰直角三角形,若,则图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
2.如图,在中,,I为各内角平分线的交点,过点I作的垂线,垂足为H,则的长为( )
A.1 B. C.2 D.
3.下列语句:①用反证法证明“”时应假设“”;②如果,,③三角形三条角平分线的交点到三角形三个顶点的距离都相等;④任意一条经过对称中心的直线可将中心对称图形分成面积相等的两部分,其中正确的个数为( )
A.1 B.2 C.3 D.4
4.如图,从电线杆离地的处向地面处拉一条长的缆绳,则处到电线杆底部处的距离为( )
A. B. C. D.
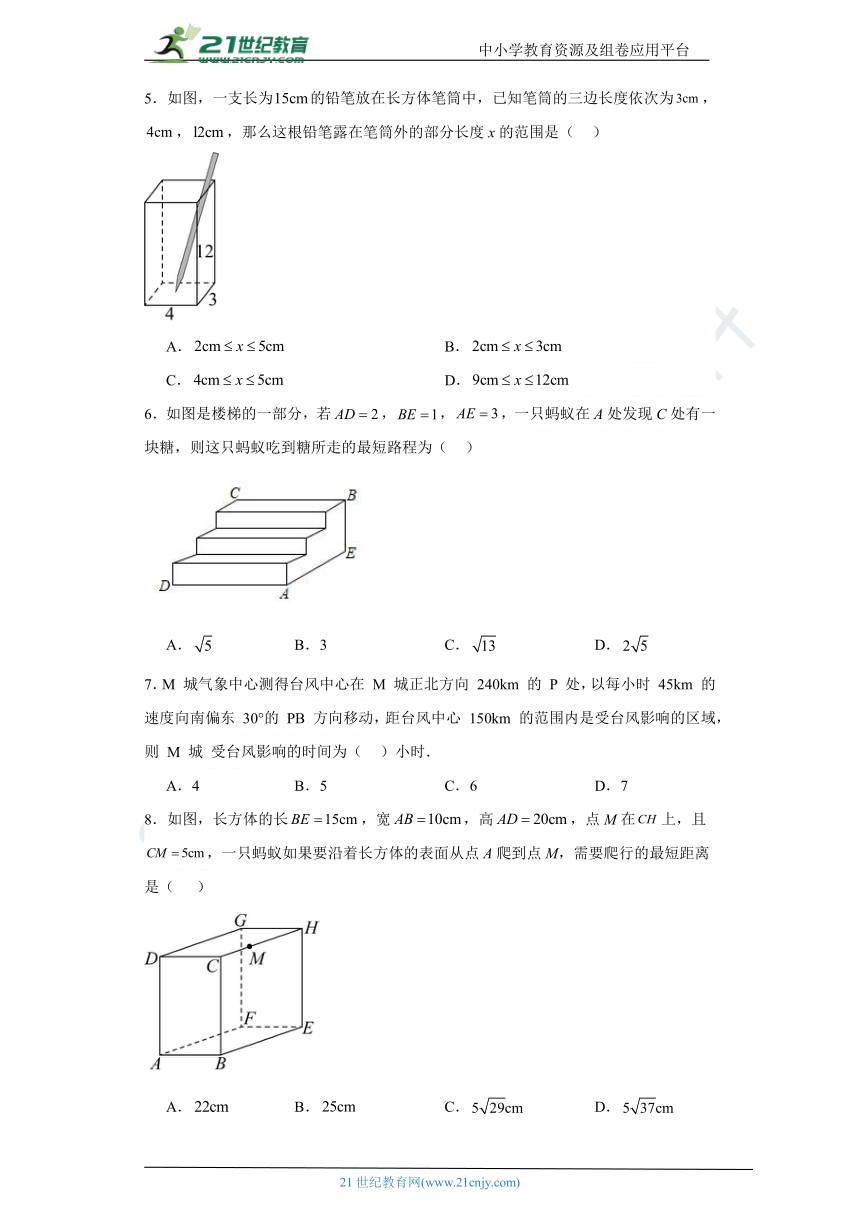
5.如图,一支长为的铅笔放在长方体笔筒中,已知笔筒的三边长度依次为,,,那么这根铅笔露在笔筒外的部分长度x的范围是( )
A. B.
C. D.
6.如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A. B.3 C. D.
7.M 城气象中心测得台风中心在 M 城正北方向 240km 的 P 处,以每小时 45km 的速度向南偏东 30°的 PB 方向移动,距台风中心 150km 的范围内是受台风影响的区域,则 M 城 受台风影响的时间为( )小时.
A.4 B.5 C.6 D.7
8.如图,长方体的长,宽,高,点M在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是( )
A. B. C. D.
二、填空题
9.如图,在网格图中,小正方形的边长均为1,点A,B,C均在小正方形的顶点上.
(1)的长为 ;
(2)点C到的距离为 .
10.如图,已知,,,.则 度.
11.小明在用反证法解答“已知中,,求证”这道题时,写出了下面的四个推理步骤:
①又因为,所以,这与三角形内角和定理相矛盾.
②所以.
③假设.
④由,得,所以.
请写出这四个步骤正确的顺序 .
12.如图,桌上有一个圆柱形玻璃杯(无盖),高厘米,底面周长厘米,在杯口内壁离杯口厘米的处有一滴蜜糖,在玻璃杯的内壁,的相对方向有一小虫,小虫离杯底的垂直距离为厘米,小虫爬到蜜糖处的最短距离是 厘米.
三、解答题
13.如图所示的是一款航模机翼部分示意图,已知,,,,请计算该机翼(四边形的周长.(结果保留根号)
14.如图,的三个顶点均在正方形网格的格点上,若小正方形的边长为1,请你运用所学的知识解决下列问题:
(1)的面积为__________;
(2)判断的形状,并说明理由.
15.用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,,,都被所截.
求证:.
证明:假设 ,
∵,
∴ ,
∵,
∴ ,这与 矛盾,
∴假设 不成立,即;
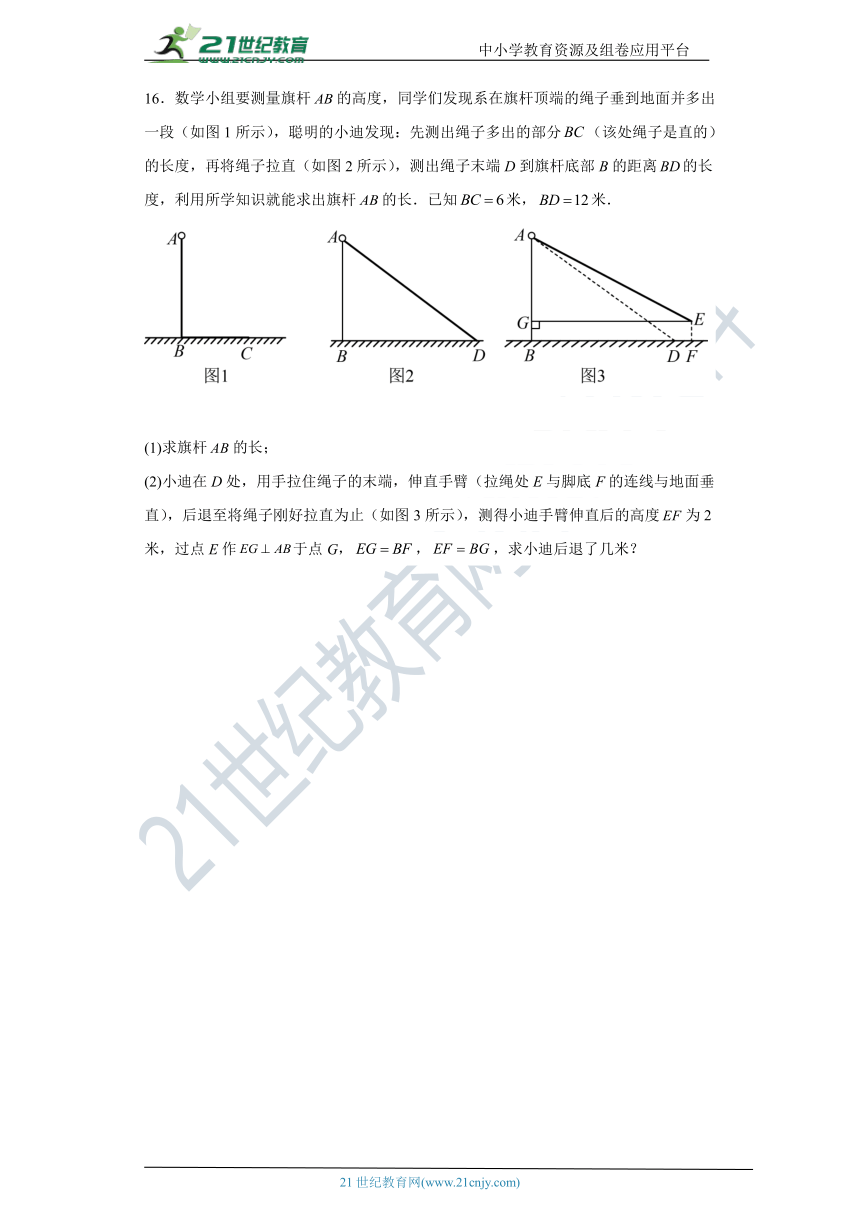
16.数学小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1所示),聪明的小迪发现:先测出绳子多出的部分(该处绳子是直的)的长度,再将绳子拉直(如图2所示),测出绳子末端D到旗杆底部B的距离的长度,利用所学知识就能求出旗杆的长.已知米,米.
(1)求旗杆的长;
(2)小迪在D处,用手拉住绳子的末端,伸直手臂(拉绳处E与脚底F的连线与地面垂直),后退至将绳子刚好拉直为止(如图3所示),测得小迪手臂伸直后的高度为2米,过点E作于点G,,,求小迪后退了几米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】先用直角三角形的边长表示出阴影部分的面积, 再根据勾股定理可得: , 进而可将阴影部分的面积求出.
【详解】解:,
在中
,
,
,
故选:C.
【点睛】本题考查了勾股定理的知识,要求能够运用勾股定理证明三个等腰直角三角形的面积之间的关系.
2.A
【分析】过点I作,垂足为E,过点I作,垂足为D,连接,,,先利用角平分线的性质可得,再利用勾股定理的逆定理证明△ABC是直角三角形,从而可得,然后利用面积法进行计算,即可解答.
【详解】解:过点I作,垂足为E,过点I作,垂足为D,连接,,,
∵I为各内角平分线的交点,,,,
∴,
∵,
∴,,
∴,
∴是直角三角形,
∴,
∵的面积的面积的面积的面积,
∴,
∴,
∴,
解得:,
故选:A.
【点睛】本题考查了勾股定理的逆定理,角平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
3.A
【分析】根据反证法,不等式的性质,三角形角平分线性质以及中心对称图形进行分析判断.
【详解】①用反证法证明“”时应假设“”,故①错误;
②如果 且,则,如果,则,故②错误;
③三角形三条角平分线的交点到这个三角形三边距离都相等,三角形三边垂直平分线的交点到三角形三个顶点的距离都相等,故③错误;
④任意一条经过对称中心的直线可将中心对称图形分为面积相等的两部分,因为这条直线的一边绕着这个对称中心旋转180°后会与另一边重合,即两边图形全等,故④正确.
所以正确的有:④,只有一个.
故选:A.
【点睛】本题主要考查了反证法,角平分线的性质,中心对称图形以及不等式的性质,属于基础题,掌握相关基础知识是解题的关键.
4.C
【分析】在中,已知斜边,一条直角边,用勾股定理求得另一条直角边即可.
【详解】解:如图:
在中,,,
,
故选:.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解答本题的关键.
5.B
【分析】由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔筒外的部分长度x最大,最大值为,由勾股定理得,长方体的对角线长为,当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度x最小,最小值为,然后作答即可.
【详解】解:由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔筒外的部分长度x最大,最大值为,
由勾股定理得,长方体的对角线长为,
当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度x最小,最小值为,
∴这根铅笔露在笔筒外的部分长度x的范围是,
故选:B.
【点睛】本题考查了勾股定理的应用.解题的关键在于对知识的熟练掌握.
6.D
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【详解】解:将台阶展开,如图,
因为DC=AE+BE=3+1=4,AD=2,
所以AC2=DC2+AD2=20,
所以AC=,
故选:D.
【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.
7.A
【分析】如图,过点M作ME⊥PB,在BP上取点F,H,设MF=MH=150km,求出FH,然后利用时间=路程÷速度,计算即可解决问题.
【详解】解:如图,过点M作ME⊥PB,在BP上取点F,H,设MF=MH=150km
在Rt△PME中,∵∠MEP=90°,PM=240km,∠MPB=30°,
∴ME=PM=120km,
∴EF=EH==90(km),
∴FH=180km,
∴受台风影响的时间有180÷45=4(小时).
故选:A
【点睛】本题考查解直角三角形的应用-方向角问题,解题的关键是理解题意,学会添加常用辅助线根据直角三角形解决问题,属于中考常考题型.
8.B
【分析】首先将长方体沿剪开,向右翻折,使面和面在同一个平面内,连接;或将长方体沿剪开,向上翻折,使面和面在同一个平面内,连接;或将长方体沿剪开,向下翻折,使面和下面在同一个平面内,连接,然后分别在与与,利用勾股定理求得的长,比较大小即可求得需要爬行的最短路程.
【详解】解:将长方体沿剪开,向右翻折,使面和面在同一个平面内,连接,如图1,
由题意可得:,
在中,根据勾股定理得:;
将长方体沿剪开,向上翻折,使面和面在同一个平面内,连接,如图2,
由题意得:,
在中,根据勾股定理得:,
将长方体沿剪开,向下翻折,使面和下面在同一个平面内,连接,如图3,
由题意得:,
在中,根据勾股定理得:,
∵,
则需要爬行的最短距离是.
故选:B.
【点睛】此题考查了最短路径问题,利用了转化的思想,解题的关键是将立体图形展为平面图形,利用勾股定理的知识求解.
9.
【分析】(1)根据勾股定理求解即可;
(2)利用等面积法求出距离即可.
【详解】解:(1)在网格图中,由勾股定理得;
故答案为:;
(2)在网格图中,由勾股定理得,
设点C到的距离为h,
∴,
∴,
解得,
∴点C到的距离为.
故答案为:.
【点睛】本题主要考查了勾股定理和网格图的理解,提高读图能力是解题的关键.
10.45
【分析】根据勾股定理得出,再利用勾股定理的逆定理解答即可.
【详解】解:∵,,
∴,
∵,
∴,
∴是直角三角形,
∵,,
∴,
∴,
故答案为:45.
【点睛】此题考查勾股定理的逆定理,关键是根据勾股定理得出BC的长.
11.③④①②
【分析】根据反证法的一般步骤解答即可.
【详解】证明:假设,
∵,
∴,
∴,
∵,
∴,这与三角形内角和定理相矛盾,
∴,
∴这四个步骤正确的顺序是③④①②.
故答案为:③④①②.
【点睛】本题考查反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.掌握反证法的一般步骤是解题的关键.也考查了等边对等角,三角形内角和定理.
12.
【分析】将杯子侧面展开,作关于杯口的对称点,根据两点之间线段最短可知的长度即为所求,再结合勾股定理求解即可.
【详解】解:如图所示:将杯子侧面展开,作关于杯口的对称点,连接,
最短距离为的长度,
厘米,
最短路程为厘米.
故答案为:.
【点睛】本题考查了平面展开最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.
13.
【详解】连接,先证明是等边三角形,求出,再证明是等腰直角三角形,根据勾股定理求出,最后相加即可.
【解答】解:连接,
,,
是等边三角形,
,,
,
,
,
,,
是等腰直角三角形,
,
该机翼(四边形的周长.
【点睛】本题考查了等边三角形的判定和性质,等腰直角三角形判定和性质,勾股定理,证明是等边三角形是解题的关键.
14.(1)5
(2)直角三角形,见解析
【分析】(1)利用包含的正方形的面积减去周围3个三角形的面积即可;
(2)利用勾股定理求出的三条边长,再利用勾股定理的逆定理判断是否是直角三角形.
【详解】(1)解:由图可得,.
故答案为:5;
(2)解:是直角三角形.
理由:由勾股定理得,,,
,
是直角三角形.
【点睛】本题考查利用网格求三角形面积,勾股定理与勾股定理的逆定理,解题的关键是熟练掌握勾股定理的逆定理.如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.
15.见解析
【分析】假设结论不成立,利用平行线性质推出矛盾即可得到答案;
【详解】证明:假设,
∵,
∴,
∵,
∴,这与平角为矛盾,
∴假设不成立,即,
故答案为:;;;平角为;.
【点睛】本题考查反正法及平行线性质,解题的关键是掌握反正法:假设结论不成立,推出矛盾.
16.(1)旗杆的长为9米
(2)小迪需要后退米
【分析】(1)在中,由勾股定理计算即可;
(2)在中,求出,根据便可求出后退的距离.
【详解】(1)解:由题意可得,,
在中,,即,
解得,即旗杆AB的长为9米;
(2)解:由题意可得,
,,
在中,,即,解得,
∴,即小迪需要后退米.
【点睛】本题主要考查了勾股定理的实际应用,属于基础题,要熟练掌握.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第14章 勾股定理 单元练习 2023-2024学年 华师大版八年级数学上册(含解析)
一、单选题
1.如图,以的三边为直角边分别向外作等腰直角三角形,若,则图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
2.如图,在中,,I为各内角平分线的交点,过点I作的垂线,垂足为H,则的长为( )
A.1 B. C.2 D.
3.下列语句:①用反证法证明“”时应假设“”;②如果,,③三角形三条角平分线的交点到三角形三个顶点的距离都相等;④任意一条经过对称中心的直线可将中心对称图形分成面积相等的两部分,其中正确的个数为( )
A.1 B.2 C.3 D.4
4.如图,从电线杆离地的处向地面处拉一条长的缆绳,则处到电线杆底部处的距离为( )
A. B. C. D.
5.如图,一支长为的铅笔放在长方体笔筒中,已知笔筒的三边长度依次为,,,那么这根铅笔露在笔筒外的部分长度x的范围是( )
A. B.
C. D.
6.如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A. B.3 C. D.
7.M 城气象中心测得台风中心在 M 城正北方向 240km 的 P 处,以每小时 45km 的速度向南偏东 30°的 PB 方向移动,距台风中心 150km 的范围内是受台风影响的区域,则 M 城 受台风影响的时间为( )小时.
A.4 B.5 C.6 D.7
8.如图,长方体的长,宽,高,点M在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是( )
A. B. C. D.
二、填空题
9.如图,在网格图中,小正方形的边长均为1,点A,B,C均在小正方形的顶点上.
(1)的长为 ;
(2)点C到的距离为 .
10.如图,已知,,,.则 度.
11.小明在用反证法解答“已知中,,求证”这道题时,写出了下面的四个推理步骤:
①又因为,所以,这与三角形内角和定理相矛盾.
②所以.
③假设.
④由,得,所以.
请写出这四个步骤正确的顺序 .
12.如图,桌上有一个圆柱形玻璃杯(无盖),高厘米,底面周长厘米,在杯口内壁离杯口厘米的处有一滴蜜糖,在玻璃杯的内壁,的相对方向有一小虫,小虫离杯底的垂直距离为厘米,小虫爬到蜜糖处的最短距离是 厘米.
三、解答题
13.如图所示的是一款航模机翼部分示意图,已知,,,,请计算该机翼(四边形的周长.(结果保留根号)
14.如图,的三个顶点均在正方形网格的格点上,若小正方形的边长为1,请你运用所学的知识解决下列问题:
(1)的面积为__________;
(2)判断的形状,并说明理由.
15.用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,,,都被所截.
求证:.
证明:假设 ,
∵,
∴ ,
∵,
∴ ,这与 矛盾,
∴假设 不成立,即;
16.数学小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1所示),聪明的小迪发现:先测出绳子多出的部分(该处绳子是直的)的长度,再将绳子拉直(如图2所示),测出绳子末端D到旗杆底部B的距离的长度,利用所学知识就能求出旗杆的长.已知米,米.
(1)求旗杆的长;
(2)小迪在D处,用手拉住绳子的末端,伸直手臂(拉绳处E与脚底F的连线与地面垂直),后退至将绳子刚好拉直为止(如图3所示),测得小迪手臂伸直后的高度为2米,过点E作于点G,,,求小迪后退了几米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】先用直角三角形的边长表示出阴影部分的面积, 再根据勾股定理可得: , 进而可将阴影部分的面积求出.
【详解】解:,
在中
,
,
,
故选:C.
【点睛】本题考查了勾股定理的知识,要求能够运用勾股定理证明三个等腰直角三角形的面积之间的关系.
2.A
【分析】过点I作,垂足为E,过点I作,垂足为D,连接,,,先利用角平分线的性质可得,再利用勾股定理的逆定理证明△ABC是直角三角形,从而可得,然后利用面积法进行计算,即可解答.
【详解】解:过点I作,垂足为E,过点I作,垂足为D,连接,,,
∵I为各内角平分线的交点,,,,
∴,
∵,
∴,,
∴,
∴是直角三角形,
∴,
∵的面积的面积的面积的面积,
∴,
∴,
∴,
解得:,
故选:A.
【点睛】本题考查了勾股定理的逆定理,角平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
3.A
【分析】根据反证法,不等式的性质,三角形角平分线性质以及中心对称图形进行分析判断.
【详解】①用反证法证明“”时应假设“”,故①错误;
②如果 且,则,如果,则,故②错误;
③三角形三条角平分线的交点到这个三角形三边距离都相等,三角形三边垂直平分线的交点到三角形三个顶点的距离都相等,故③错误;
④任意一条经过对称中心的直线可将中心对称图形分为面积相等的两部分,因为这条直线的一边绕着这个对称中心旋转180°后会与另一边重合,即两边图形全等,故④正确.
所以正确的有:④,只有一个.
故选:A.
【点睛】本题主要考查了反证法,角平分线的性质,中心对称图形以及不等式的性质,属于基础题,掌握相关基础知识是解题的关键.
4.C
【分析】在中,已知斜边,一条直角边,用勾股定理求得另一条直角边即可.
【详解】解:如图:
在中,,,
,
故选:.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解答本题的关键.
5.B
【分析】由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔筒外的部分长度x最大,最大值为,由勾股定理得,长方体的对角线长为,当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度x最小,最小值为,然后作答即可.
【详解】解:由题意知,当铅笔垂直于笔筒底部放置时,铅笔露在笔筒外的部分长度x最大,最大值为,
由勾股定理得,长方体的对角线长为,
当铅笔沿着长方体的对角线放置时,铅笔露在笔筒外的部分长度x最小,最小值为,
∴这根铅笔露在笔筒外的部分长度x的范围是,
故选:B.
【点睛】本题考查了勾股定理的应用.解题的关键在于对知识的熟练掌握.
6.D
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【详解】解:将台阶展开,如图,
因为DC=AE+BE=3+1=4,AD=2,
所以AC2=DC2+AD2=20,
所以AC=,
故选:D.
【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.
7.A
【分析】如图,过点M作ME⊥PB,在BP上取点F,H,设MF=MH=150km,求出FH,然后利用时间=路程÷速度,计算即可解决问题.
【详解】解:如图,过点M作ME⊥PB,在BP上取点F,H,设MF=MH=150km
在Rt△PME中,∵∠MEP=90°,PM=240km,∠MPB=30°,
∴ME=PM=120km,
∴EF=EH==90(km),
∴FH=180km,
∴受台风影响的时间有180÷45=4(小时).
故选:A
【点睛】本题考查解直角三角形的应用-方向角问题,解题的关键是理解题意,学会添加常用辅助线根据直角三角形解决问题,属于中考常考题型.
8.B
【分析】首先将长方体沿剪开,向右翻折,使面和面在同一个平面内,连接;或将长方体沿剪开,向上翻折,使面和面在同一个平面内,连接;或将长方体沿剪开,向下翻折,使面和下面在同一个平面内,连接,然后分别在与与,利用勾股定理求得的长,比较大小即可求得需要爬行的最短路程.
【详解】解:将长方体沿剪开,向右翻折,使面和面在同一个平面内,连接,如图1,
由题意可得:,
在中,根据勾股定理得:;
将长方体沿剪开,向上翻折,使面和面在同一个平面内,连接,如图2,
由题意得:,
在中,根据勾股定理得:,
将长方体沿剪开,向下翻折,使面和下面在同一个平面内,连接,如图3,
由题意得:,
在中,根据勾股定理得:,
∵,
则需要爬行的最短距离是.
故选:B.
【点睛】此题考查了最短路径问题,利用了转化的思想,解题的关键是将立体图形展为平面图形,利用勾股定理的知识求解.
9.
【分析】(1)根据勾股定理求解即可;
(2)利用等面积法求出距离即可.
【详解】解:(1)在网格图中,由勾股定理得;
故答案为:;
(2)在网格图中,由勾股定理得,
设点C到的距离为h,
∴,
∴,
解得,
∴点C到的距离为.
故答案为:.
【点睛】本题主要考查了勾股定理和网格图的理解,提高读图能力是解题的关键.
10.45
【分析】根据勾股定理得出,再利用勾股定理的逆定理解答即可.
【详解】解:∵,,
∴,
∵,
∴,
∴是直角三角形,
∵,,
∴,
∴,
故答案为:45.
【点睛】此题考查勾股定理的逆定理,关键是根据勾股定理得出BC的长.
11.③④①②
【分析】根据反证法的一般步骤解答即可.
【详解】证明:假设,
∵,
∴,
∴,
∵,
∴,这与三角形内角和定理相矛盾,
∴,
∴这四个步骤正确的顺序是③④①②.
故答案为:③④①②.
【点睛】本题考查反证法,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.掌握反证法的一般步骤是解题的关键.也考查了等边对等角,三角形内角和定理.
12.
【分析】将杯子侧面展开,作关于杯口的对称点,根据两点之间线段最短可知的长度即为所求,再结合勾股定理求解即可.
【详解】解:如图所示:将杯子侧面展开,作关于杯口的对称点,连接,
最短距离为的长度,
厘米,
最短路程为厘米.
故答案为:.
【点睛】本题考查了平面展开最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.
13.
【详解】连接,先证明是等边三角形,求出,再证明是等腰直角三角形,根据勾股定理求出,最后相加即可.
【解答】解:连接,
,,
是等边三角形,
,,
,
,
,
,,
是等腰直角三角形,
,
该机翼(四边形的周长.
【点睛】本题考查了等边三角形的判定和性质,等腰直角三角形判定和性质,勾股定理,证明是等边三角形是解题的关键.
14.(1)5
(2)直角三角形,见解析
【分析】(1)利用包含的正方形的面积减去周围3个三角形的面积即可;
(2)利用勾股定理求出的三条边长,再利用勾股定理的逆定理判断是否是直角三角形.
【详解】(1)解:由图可得,.
故答案为:5;
(2)解:是直角三角形.
理由:由勾股定理得,,,
,
是直角三角形.
【点睛】本题考查利用网格求三角形面积,勾股定理与勾股定理的逆定理,解题的关键是熟练掌握勾股定理的逆定理.如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.
15.见解析
【分析】假设结论不成立,利用平行线性质推出矛盾即可得到答案;
【详解】证明:假设,
∵,
∴,
∵,
∴,这与平角为矛盾,
∴假设不成立,即,
故答案为:;;;平角为;.
【点睛】本题考查反正法及平行线性质,解题的关键是掌握反正法:假设结论不成立,推出矛盾.
16.(1)旗杆的长为9米
(2)小迪需要后退米
【分析】(1)在中,由勾股定理计算即可;
(2)在中,求出,根据便可求出后退的距离.
【详解】(1)解:由题意可得,,
在中,,即,
解得,即旗杆AB的长为9米;
(2)解:由题意可得,
,,
在中,,即,解得,
∴,即小迪需要后退米.
【点睛】本题主要考查了勾股定理的实际应用,属于基础题,要熟练掌握.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
