第25章 随机事件的概率 单元练习 2023-2024学年 华师大版九年级数学上册(含解析)
文档属性
| 名称 | 第25章 随机事件的概率 单元练习 2023-2024学年 华师大版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 806.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 15:38:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第25章 随机事件的概率 单元练习 2023-2024学年 华师大版九年级数学上册(含解析)
一、单选题
1.“一次抛三枚均匀的骰子,朝上一面的点数都为6”这一事件是( )
A.必然事件 B.确定事件 C.随机事件 D.不可能事件
2.下列所给的事件中,是必然事件的是( )
A.买注福利彩票会中奖
B.某校的名学生中,至少有名学生的生日是同一天
C.连续次投掷质地均匀的硬币,会有次硬币正面朝上
D.年的春节假期长沙会下雪
3.袋中有红球4个,白球若干个,它们只有颜色上的区别.从袋中随机地取出一个球,如果取到白球的概率较大,那么袋中白球的个数可能是( ).
A.2 B.3 C.4 D.5
4.下列说法中正确的是( )
A.为了了解我国中学生的课外阅读情况,应采取全面调查方式
B.某彩票的中奖机会是,买100张一定会中奖
C.若a是实数,则是必然事件
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定
5.某射击运动员在同一条件下射击,结果如表所示:根据频率的稳定性,这名运动员射击一次击中靶心的概率约是( )
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 8 17 40 79 158 390 780
击中靶心的频率
A. B. C. D.
6.某校举行安全系列教育活动主题手抄报的评比活动,学校共设置了“交通安全”“消防安全”“饮食安全”“校园安全”四个主题内容.一班推荐李明与张颖参加手抄报评比,他们两人选取同一个主题的概率是( )
A. B. C. D.
二、填空题
7.现有1,2,3,…,9九个数字,甲、乙两位同学轮流从中选出一个数字,从左至右依次填入下面所示的表格中(表中已出现的数字不再重复使用),每次填数时,甲会选择填入后使表中现有数据平均数最小的数字,乙会选择填入后使表中现有数据中位数最小的数字.如图,若表中第一个数字是6,甲先填,
(1)请你在表中空白处填出一种符合要求的填数结果 ;
(2)满足条件的填法有 种.
6
8.某航班每次约有200名乘客,一次飞行中飞机失事的概率,某保险公司为乘客提供保险,承诺飞机一旦失事,向每位乘客赔偿60万人民币.平均来说,保险公司应该至少向每位乘客收取 元保险费才不亏本.
9.一名球员在罚球线上投篮的结果记录如下表:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 123 152 251
投中频率
先将表中数据补全(精确到);根据以上数据可以估计,这名球员投篮一次.投中的概率约是 (精确到).
10.图1是沐沐用正方形纸板制作的七巧板,图2是用该七巧板拼出的“一帆风顺”飞镖盘,若沐沐每次扔飞镖时,飞镖都能掷在盘上,则随机投掷一次,掷在图中涂色部分的概率是 .
三、解答题
11.为了提高学生阅读能力,某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)本次调查的学生有________人;请将条形统计图补充完整;
(2)扇形统计图中,求出“1.5小时”部分所对的扇形圆心角度数;
(3)若该校八年级共有500人,现从中随机抽取一名学生,你认为“抽到周末阅读时间为1.5小时的学生”与“抽到周末阅读时间不高于1小时的学生”的可能性哪个大?________.(直接写出结果)
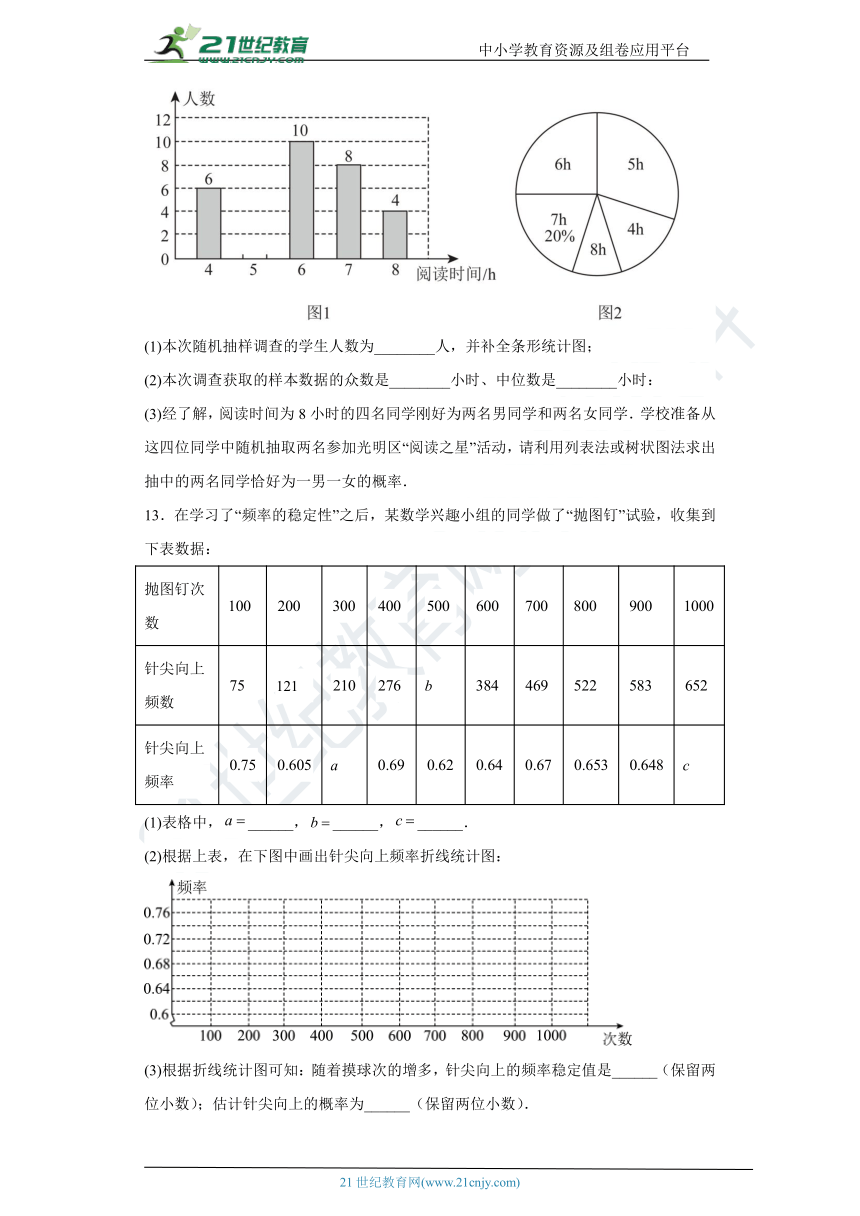
12.光明区某学校为了了解学生课外阅读的情况,从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调查,并绘制出如下两幅统计图.根据相关信息,解答下列问题.
(1)本次随机抽样调查的学生人数为________人,并补全条形统计图;
(2)本次调查获取的样本数据的众数是________小时、中位数是________小时:
(3)经了解,阅读时间为8小时的四名同学刚好为两名男同学和两名女同学.学校准备从这四位同学中随机抽取两名参加光明区“阅读之星”活动,请利用列表法或树状图法求出抽中的两名同学恰好为一男一女的概率.
13.在学习了“频率的稳定性”之后,某数学兴趣小组的同学做了“抛图钉”试验,收集到下表数据:
抛图钉次数
针尖向上频数 b
针尖向上频率 a c
(1)表格中,______,______,______.
(2)根据上表,在下图中画出针尖向上频率折线统计图:
(3)根据折线统计图可知:随着摸球次的增多,针尖向上的频率稳定值是______(保留两位小数);估计针尖向上的概率为______(保留两位小数).
14.由于要上物理实验课,物理老师要求物理学习委员在上课前打开物理实验室的门,并给学习委员一串带有5把钥匙(外形材质无差别)的钥匙扣,其中只有两把钥匙能打开物理实验室的门.
(1)学习委员“试第一把钥匙就打开物理实验室门”是________事件(填“不可能”或“必然”或“随机”);学习委员“试第一把钥匙未打开物理实验室门”的概率是________;
(2)若学习委员随机抽取两把钥匙开实验室的门,请用画树状图或列表的方法表示出所有可能结果,并求出学习委员试第二把钥匙时才打开实验室门的概率.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】根据事件发生的可能性大小判断相应事件的类型即可.
【详解】解:“一次抛六枚均匀的骰子,朝上一面的点数都为6”这一事件是随机事件,
故选C.
【点睛】本题考查随机事件,解决本题关键是正确理解必然事件、随机事件、不可能事件的概念.
2.B
【分析】根据必然事件、不可能事件、随机事件的概念可区别各类事件.
【详解】解:A、买注福利彩票会中奖是随机事件,故本选项不符合题意;
B、某校的名学生中,至少有名学生的生日是同一天是必然事件,故本选项不符合题意;
C、连续次投掷质地均匀的硬币,会有次硬币正面朝上是随机事件,故本选项不符合题意;
D、年的春节假期长沙会下雪是随机事件,故本选项不符合题意.
故选:B.
【点睛】本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
3.D
【分析】根据概率公式求出白球的取值范围即可得出结论.
【详解】解:若要使取到白球的概率较大,则白球的个数>红球的个数
由各选项可知,只有D选项符合
故选D.
【点睛】此题考查的是比较概率的大小,掌握概率公式是解决此题的关键.
4.D
【分析】直接利用概率的意义以及必然事件、全面调查的意义分别分析得出答案.
【详解】解:A.为了了解我国中学生的课外阅读情况,应采取抽样调查方式,原说法错误,故此选项不合题意;
B.某彩票的中奖机会是,买100张也不一定会中奖,原说法错误,故此选项不合题意;
C.若a是实数,则是随机事件,原说法错误,故此选项不合题意;
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定,故此选项符合题意,
故选:D.
【点睛】此题主要考查了概率的意义以及方差,正确掌握概率的意义是解题关键.
5.A
【分析】利用频率估计概率求解即可;
【详解】解:根据频率的稳定性,估计这名运动员射击一次时击中靶心的概率约是,
故选:A.
【点睛】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,理解这个固定的近似值就是这个事件的概率是解题的关键
6.B
【分析】画树状图,共有16种等可能的结果,其中李明与张颖他们两人选取同一个主题的结果有4种,再由概率公式求解即可.
【详解】解:把“交通安全”“消防安全”“饮食安全”“校园安全”四个主题内容分别记为A、B、C、D,
画树状图如下:
共有16种等可能的结果,其中李明与张颖两人选取同一个主题的结果有4种,
∴李明与张颖两人选取同一个主题的概率是,
故选:B.
【点睛】本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
7.
【分析】根据填数时,甲会选择填入后使表中现有数据平均数最大的数字,可知,甲每次都会选最大的数字;再根据乙选择数字的方法判断满足条件的填法即可.
【详解】解:甲会选择填入后使表中现有数据平均数最大的数字,表中第一个数字是,甲先填,
第二个数字为,第四个数字为,
乙会选择填入后使表中现有数据中位数最小的数字.
第三个数字可以为,,,,,第五个数字可以为,,,,且不能与第三个数字相同,即第三个数字有种选法,第五个数字有种选法,
满足条件的填法有种,表中空白处可以为.
故答案为:,
【点睛】本题考查平均数,中位数的定义,列举法,解题的关键是理解甲选数字的方法,乙选数字的方法,根据其选数字的方法知道其所选数字.
8.30
【分析】先求出飞机失事时保险公司应赔偿的金额,再根据飞机失事的概率求出赔偿的钱数即可解答.
【详解】解:每次约有200名乘客,如飞机一旦失事,每位乘客赔偿60万人民币,共计12000万元,
一次飞行中飞机失事的概率为,
故赔偿的钱数为元,
故至少应该收取保险费每人元,
故答案为:30.
【点睛】本题考查的是概率在现实生活中的运用,部分数目=总体数目乘以相应概率.
9.
【分析】用投中的次数除以投篮的次数即可补全表中数据;根据表中数据可得,随着投篮次数越来越大时,频率逐渐稳定到常数0.50附近,
【详解】解:,
由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数附近,
∴这名球员在罚球线上投篮一次,投中的概率为.
故答案为:.
【点睛】此题考查了利用频率估计概率的知识,解题的关键是理解这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.
10./
【分析】如图,由正方形及七巧板的特征可得:,,,,证明,可得,再结合概率公式即可得到结论.
【详解】解:如图,由正方形及七巧板的特征可得:
,,,,
∴,
∴,
∴,
∴阴影部分的面积是七巧板面积的,
故掷在图中涂色部分的概率是.
故答案为:.
【点睛】本题主要考查几何概率,相似三角形的判定与性质,求概率时计算方法是长度比,面积比,体积比等.
11.(1)100人,见解析
(2)144°;
(3)“抽到周末阅读时间不高于1小时的学生”的可能性大.
【分析】(1)根据阅读时间1小时的人数和所占的百分比,可以求得本次调查的人数,然后即可计算出阅读时间为1.5小时的人数,从而可以将条形统计图补充完整;
(2)用“1.5小时”部分所对的扇形所占的百分比乘以360°即可求得答案;
(3)分别求得可能性大小后比较即可确定正确的答案.
【详解】(1)本次调查的学生有30÷30%=100(人),
阅读1.5小时的学生有:100-12-30-18=40(人),
补全的条形统计图如右图所示,
故答案为:100;
(2)360°×=144°,
即“1.5小时”部分所对的扇形圆心角度数144°;
(3)“抽到周末阅读时间为1.5小时的学生”的可能性为;
“抽到周末阅读时间不高于1小时的学生”的可能性为,
∴“抽到周末阅读时间不高于1小时的学生”的可能性大.
故答案为:“抽到周末阅读时间不高于1小时的学生”的可能性大.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体、加权平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
12.(1)40,图见解析
(2)5,6
(3)
【分析】(1)根据条形图中阅读时间7h的有8人,扇形图中阅读时间7h的比例为20%,即可计算出调查的学生人数;调查的学生人数减去已知的各个阅读时间的人数即可得到阅读时间5h的学生人数,就可补全条形统计图;
(2)阅读时间5h的人数最多,因此众数是5.将数据排序,处于中间位置的数是6,6,因此中位数是.
(3)用列表法或树状图法列出所有的等可能结果,再找出满足要求的结果,即可求出所求抽中的两名同学恰好为一男一女的概率.
【详解】(1)由条形图中阅读时间7h的有8人,扇形图中阅读时间7h的比例为20%,可得调查的人数为:(人)
阅读时间5h的学生人数为:(人)
故答案为:40,补充图如下:
(2)阅读时间5h的人数最多,因此众数是5.
将数据排序,处于中间位置的数是6,6,因此中位数是.
故答案为:5,6;
(3)由前可知,有4名同学,其中男生、女生各2名,分别用A,B表示男生,用C,D表示女生,利用列表法列出所有可能出现的结果:
A B C D
A × (A,B) (A,C) (A,D)
B (A,B) × (B,C) (B,D)
C (A,C) (B,C) × (C,D)
D (A,D) (B,D) (C,D) ×
总共有12种等可能的结果,恰好一男一女结果有8种:
所以,P(一男一女).
【点睛】本题主要考查统计图表,列举法求概率.正确理解各个知识是解题的关键.
13.(1);;
(2)见解析
(3);
【分析】(1)根据频率、频数、总数之间的关系填写表格即可求解;
(2)根据表格数据,画出频率折线统计图即可求解;
(3)利用大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】(1)解:,,,
故答案为:;;.
(2)解:如图所示,
(3)解:根据折线统计图可知:随着摸球次的增多,针尖向上的频率稳定值是(保留两位小数);估计针尖向上的概率为(保留两位小数),
故答案为:;.
【点睛】本题考查了频数、频率之间的关系,画折线统计图,根据频率估计概率,熟练掌握以上知识是解题的关键.
14.(1)随机,
(2)图见解析,
【分析】(1)根据事件的分类,以及概率公式即可进行解答;
(2)根据题意,画出树状图,数出所有符合条件的情况数和总情况数,用概率公式求解即可.
【详解】(1)解:∵试第一把钥匙有可能打开物理实验室门,也有可能打不开物理实验室门,
∴“试第一把钥匙就打开物理实验室门”是随机事件,
∵一共有5把钥匙(外形材质无差别),其中只有两把钥匙能打开物理实验室的门,
∴“试第一把钥匙未打开物理实验室门”的概率是,
故答案为:随机,;
(2)记5把钥匙分别为A、B、C、D、E,其中能打开的为A、B两把钥匙,画树状图如解图:
由树状图可知,共有20种等可能情况,其中试第二把钥匙时才打开实验室门有6种情况,
∴.
【点睛】本题考查了列表法或树状图法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第25章 随机事件的概率 单元练习 2023-2024学年 华师大版九年级数学上册(含解析)
一、单选题
1.“一次抛三枚均匀的骰子,朝上一面的点数都为6”这一事件是( )
A.必然事件 B.确定事件 C.随机事件 D.不可能事件
2.下列所给的事件中,是必然事件的是( )
A.买注福利彩票会中奖
B.某校的名学生中,至少有名学生的生日是同一天
C.连续次投掷质地均匀的硬币,会有次硬币正面朝上
D.年的春节假期长沙会下雪
3.袋中有红球4个,白球若干个,它们只有颜色上的区别.从袋中随机地取出一个球,如果取到白球的概率较大,那么袋中白球的个数可能是( ).
A.2 B.3 C.4 D.5
4.下列说法中正确的是( )
A.为了了解我国中学生的课外阅读情况,应采取全面调查方式
B.某彩票的中奖机会是,买100张一定会中奖
C.若a是实数,则是必然事件
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定
5.某射击运动员在同一条件下射击,结果如表所示:根据频率的稳定性,这名运动员射击一次击中靶心的概率约是( )
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 8 17 40 79 158 390 780
击中靶心的频率
A. B. C. D.
6.某校举行安全系列教育活动主题手抄报的评比活动,学校共设置了“交通安全”“消防安全”“饮食安全”“校园安全”四个主题内容.一班推荐李明与张颖参加手抄报评比,他们两人选取同一个主题的概率是( )
A. B. C. D.
二、填空题
7.现有1,2,3,…,9九个数字,甲、乙两位同学轮流从中选出一个数字,从左至右依次填入下面所示的表格中(表中已出现的数字不再重复使用),每次填数时,甲会选择填入后使表中现有数据平均数最小的数字,乙会选择填入后使表中现有数据中位数最小的数字.如图,若表中第一个数字是6,甲先填,
(1)请你在表中空白处填出一种符合要求的填数结果 ;
(2)满足条件的填法有 种.
6
8.某航班每次约有200名乘客,一次飞行中飞机失事的概率,某保险公司为乘客提供保险,承诺飞机一旦失事,向每位乘客赔偿60万人民币.平均来说,保险公司应该至少向每位乘客收取 元保险费才不亏本.
9.一名球员在罚球线上投篮的结果记录如下表:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 123 152 251
投中频率
先将表中数据补全(精确到);根据以上数据可以估计,这名球员投篮一次.投中的概率约是 (精确到).
10.图1是沐沐用正方形纸板制作的七巧板,图2是用该七巧板拼出的“一帆风顺”飞镖盘,若沐沐每次扔飞镖时,飞镖都能掷在盘上,则随机投掷一次,掷在图中涂色部分的概率是 .
三、解答题
11.为了提高学生阅读能力,某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)本次调查的学生有________人;请将条形统计图补充完整;
(2)扇形统计图中,求出“1.5小时”部分所对的扇形圆心角度数;
(3)若该校八年级共有500人,现从中随机抽取一名学生,你认为“抽到周末阅读时间为1.5小时的学生”与“抽到周末阅读时间不高于1小时的学生”的可能性哪个大?________.(直接写出结果)
12.光明区某学校为了了解学生课外阅读的情况,从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调查,并绘制出如下两幅统计图.根据相关信息,解答下列问题.
(1)本次随机抽样调查的学生人数为________人,并补全条形统计图;
(2)本次调查获取的样本数据的众数是________小时、中位数是________小时:
(3)经了解,阅读时间为8小时的四名同学刚好为两名男同学和两名女同学.学校准备从这四位同学中随机抽取两名参加光明区“阅读之星”活动,请利用列表法或树状图法求出抽中的两名同学恰好为一男一女的概率.
13.在学习了“频率的稳定性”之后,某数学兴趣小组的同学做了“抛图钉”试验,收集到下表数据:
抛图钉次数
针尖向上频数 b
针尖向上频率 a c
(1)表格中,______,______,______.
(2)根据上表,在下图中画出针尖向上频率折线统计图:
(3)根据折线统计图可知:随着摸球次的增多,针尖向上的频率稳定值是______(保留两位小数);估计针尖向上的概率为______(保留两位小数).
14.由于要上物理实验课,物理老师要求物理学习委员在上课前打开物理实验室的门,并给学习委员一串带有5把钥匙(外形材质无差别)的钥匙扣,其中只有两把钥匙能打开物理实验室的门.
(1)学习委员“试第一把钥匙就打开物理实验室门”是________事件(填“不可能”或“必然”或“随机”);学习委员“试第一把钥匙未打开物理实验室门”的概率是________;
(2)若学习委员随机抽取两把钥匙开实验室的门,请用画树状图或列表的方法表示出所有可能结果,并求出学习委员试第二把钥匙时才打开实验室门的概率.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】根据事件发生的可能性大小判断相应事件的类型即可.
【详解】解:“一次抛六枚均匀的骰子,朝上一面的点数都为6”这一事件是随机事件,
故选C.
【点睛】本题考查随机事件,解决本题关键是正确理解必然事件、随机事件、不可能事件的概念.
2.B
【分析】根据必然事件、不可能事件、随机事件的概念可区别各类事件.
【详解】解:A、买注福利彩票会中奖是随机事件,故本选项不符合题意;
B、某校的名学生中,至少有名学生的生日是同一天是必然事件,故本选项不符合题意;
C、连续次投掷质地均匀的硬币,会有次硬币正面朝上是随机事件,故本选项不符合题意;
D、年的春节假期长沙会下雪是随机事件,故本选项不符合题意.
故选:B.
【点睛】本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
3.D
【分析】根据概率公式求出白球的取值范围即可得出结论.
【详解】解:若要使取到白球的概率较大,则白球的个数>红球的个数
由各选项可知,只有D选项符合
故选D.
【点睛】此题考查的是比较概率的大小,掌握概率公式是解决此题的关键.
4.D
【分析】直接利用概率的意义以及必然事件、全面调查的意义分别分析得出答案.
【详解】解:A.为了了解我国中学生的课外阅读情况,应采取抽样调查方式,原说法错误,故此选项不合题意;
B.某彩票的中奖机会是,买100张也不一定会中奖,原说法错误,故此选项不合题意;
C.若a是实数,则是随机事件,原说法错误,故此选项不合题意;
D.甲、乙两组数据方差分别为和,则甲组数据比乙组数据稳定,故此选项符合题意,
故选:D.
【点睛】此题主要考查了概率的意义以及方差,正确掌握概率的意义是解题关键.
5.A
【分析】利用频率估计概率求解即可;
【详解】解:根据频率的稳定性,估计这名运动员射击一次时击中靶心的概率约是,
故选:A.
【点睛】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,理解这个固定的近似值就是这个事件的概率是解题的关键
6.B
【分析】画树状图,共有16种等可能的结果,其中李明与张颖他们两人选取同一个主题的结果有4种,再由概率公式求解即可.
【详解】解:把“交通安全”“消防安全”“饮食安全”“校园安全”四个主题内容分别记为A、B、C、D,
画树状图如下:
共有16种等可能的结果,其中李明与张颖两人选取同一个主题的结果有4种,
∴李明与张颖两人选取同一个主题的概率是,
故选:B.
【点睛】本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
7.
【分析】根据填数时,甲会选择填入后使表中现有数据平均数最大的数字,可知,甲每次都会选最大的数字;再根据乙选择数字的方法判断满足条件的填法即可.
【详解】解:甲会选择填入后使表中现有数据平均数最大的数字,表中第一个数字是,甲先填,
第二个数字为,第四个数字为,
乙会选择填入后使表中现有数据中位数最小的数字.
第三个数字可以为,,,,,第五个数字可以为,,,,且不能与第三个数字相同,即第三个数字有种选法,第五个数字有种选法,
满足条件的填法有种,表中空白处可以为.
故答案为:,
【点睛】本题考查平均数,中位数的定义,列举法,解题的关键是理解甲选数字的方法,乙选数字的方法,根据其选数字的方法知道其所选数字.
8.30
【分析】先求出飞机失事时保险公司应赔偿的金额,再根据飞机失事的概率求出赔偿的钱数即可解答.
【详解】解:每次约有200名乘客,如飞机一旦失事,每位乘客赔偿60万人民币,共计12000万元,
一次飞行中飞机失事的概率为,
故赔偿的钱数为元,
故至少应该收取保险费每人元,
故答案为:30.
【点睛】本题考查的是概率在现实生活中的运用,部分数目=总体数目乘以相应概率.
9.
【分析】用投中的次数除以投篮的次数即可补全表中数据;根据表中数据可得,随着投篮次数越来越大时,频率逐渐稳定到常数0.50附近,
【详解】解:,
由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数附近,
∴这名球员在罚球线上投篮一次,投中的概率为.
故答案为:.
【点睛】此题考查了利用频率估计概率的知识,解题的关键是理解这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.
10./
【分析】如图,由正方形及七巧板的特征可得:,,,,证明,可得,再结合概率公式即可得到结论.
【详解】解:如图,由正方形及七巧板的特征可得:
,,,,
∴,
∴,
∴,
∴阴影部分的面积是七巧板面积的,
故掷在图中涂色部分的概率是.
故答案为:.
【点睛】本题主要考查几何概率,相似三角形的判定与性质,求概率时计算方法是长度比,面积比,体积比等.
11.(1)100人,见解析
(2)144°;
(3)“抽到周末阅读时间不高于1小时的学生”的可能性大.
【分析】(1)根据阅读时间1小时的人数和所占的百分比,可以求得本次调查的人数,然后即可计算出阅读时间为1.5小时的人数,从而可以将条形统计图补充完整;
(2)用“1.5小时”部分所对的扇形所占的百分比乘以360°即可求得答案;
(3)分别求得可能性大小后比较即可确定正确的答案.
【详解】(1)本次调查的学生有30÷30%=100(人),
阅读1.5小时的学生有:100-12-30-18=40(人),
补全的条形统计图如右图所示,
故答案为:100;
(2)360°×=144°,
即“1.5小时”部分所对的扇形圆心角度数144°;
(3)“抽到周末阅读时间为1.5小时的学生”的可能性为;
“抽到周末阅读时间不高于1小时的学生”的可能性为,
∴“抽到周末阅读时间不高于1小时的学生”的可能性大.
故答案为:“抽到周末阅读时间不高于1小时的学生”的可能性大.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体、加权平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
12.(1)40,图见解析
(2)5,6
(3)
【分析】(1)根据条形图中阅读时间7h的有8人,扇形图中阅读时间7h的比例为20%,即可计算出调查的学生人数;调查的学生人数减去已知的各个阅读时间的人数即可得到阅读时间5h的学生人数,就可补全条形统计图;
(2)阅读时间5h的人数最多,因此众数是5.将数据排序,处于中间位置的数是6,6,因此中位数是.
(3)用列表法或树状图法列出所有的等可能结果,再找出满足要求的结果,即可求出所求抽中的两名同学恰好为一男一女的概率.
【详解】(1)由条形图中阅读时间7h的有8人,扇形图中阅读时间7h的比例为20%,可得调查的人数为:(人)
阅读时间5h的学生人数为:(人)
故答案为:40,补充图如下:
(2)阅读时间5h的人数最多,因此众数是5.
将数据排序,处于中间位置的数是6,6,因此中位数是.
故答案为:5,6;
(3)由前可知,有4名同学,其中男生、女生各2名,分别用A,B表示男生,用C,D表示女生,利用列表法列出所有可能出现的结果:
A B C D
A × (A,B) (A,C) (A,D)
B (A,B) × (B,C) (B,D)
C (A,C) (B,C) × (C,D)
D (A,D) (B,D) (C,D) ×
总共有12种等可能的结果,恰好一男一女结果有8种:
所以,P(一男一女).
【点睛】本题主要考查统计图表,列举法求概率.正确理解各个知识是解题的关键.
13.(1);;
(2)见解析
(3);
【分析】(1)根据频率、频数、总数之间的关系填写表格即可求解;
(2)根据表格数据,画出频率折线统计图即可求解;
(3)利用大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】(1)解:,,,
故答案为:;;.
(2)解:如图所示,
(3)解:根据折线统计图可知:随着摸球次的增多,针尖向上的频率稳定值是(保留两位小数);估计针尖向上的概率为(保留两位小数),
故答案为:;.
【点睛】本题考查了频数、频率之间的关系,画折线统计图,根据频率估计概率,熟练掌握以上知识是解题的关键.
14.(1)随机,
(2)图见解析,
【分析】(1)根据事件的分类,以及概率公式即可进行解答;
(2)根据题意,画出树状图,数出所有符合条件的情况数和总情况数,用概率公式求解即可.
【详解】(1)解:∵试第一把钥匙有可能打开物理实验室门,也有可能打不开物理实验室门,
∴“试第一把钥匙就打开物理实验室门”是随机事件,
∵一共有5把钥匙(外形材质无差别),其中只有两把钥匙能打开物理实验室的门,
∴“试第一把钥匙未打开物理实验室门”的概率是,
故答案为:随机,;
(2)记5把钥匙分别为A、B、C、D、E,其中能打开的为A、B两把钥匙,画树状图如解图:
由树状图可知,共有20种等可能情况,其中试第二把钥匙时才打开实验室门有6种情况,
∴.
【点睛】本题考查了列表法或树状图法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
