9.3.2向量的坐标表示及运算 课件(共33张PPT) 高一下学期数学苏教版(2019)必修第二册
文档属性
| 名称 | 9.3.2向量的坐标表示及运算 课件(共33张PPT) 高一下学期数学苏教版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 997.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
第9章 平面向量
9.3.2 向量坐标表示与运算
在物理中,力是一个向量,力的合成就是向量的加法运算.力也可以分解,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论.
引入
一、向量的坐标表示及坐标运算
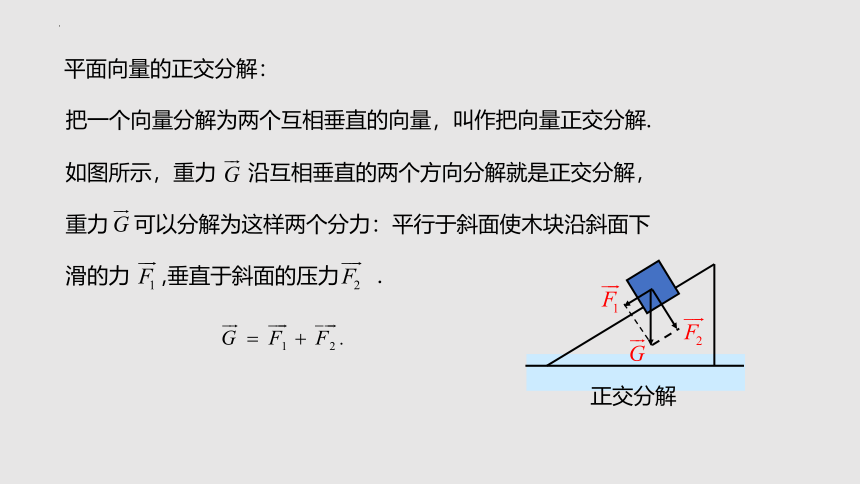
平面向量的正交分解:
把一个向量分解为两个互相垂直的向量,叫作把向量正交分解.
如图所示,重力 沿互相垂直的两个方向分解就是正交分解,
重力 可以分解为这样两个分力:平行于斜面使木块沿斜面下
滑的力 ,垂直于斜面的压力 .
正交分解
平面向量的正交分解:
如图,向量 , 是两个互相垂直的单位向量,向量 与 的夹角是30°,
且 ,以向量 , 为一组基,向量 如何表示?
思考:在平面直角坐标系中,每一个点都可用一对有序实数表示,
那么,如何表示直角坐标平面的一个向量呢?
在平面上,如果选取互相垂直的向量作为一组基时,将为我们研究
问题带来方便.
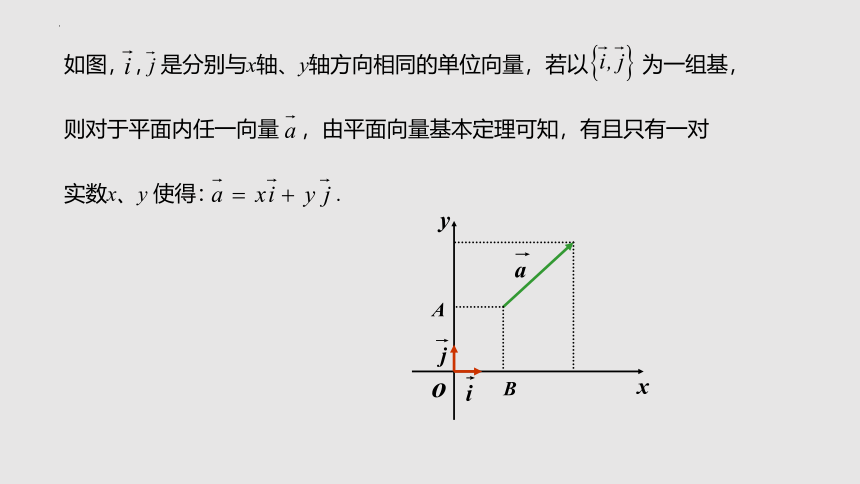
如图, , 是分别与x轴、y轴方向相同的单位向量,若以 为一组基,
则对于平面内任一向量 ,由平面向量基本定理可知,有且只有一对
实数x、y 使得: .
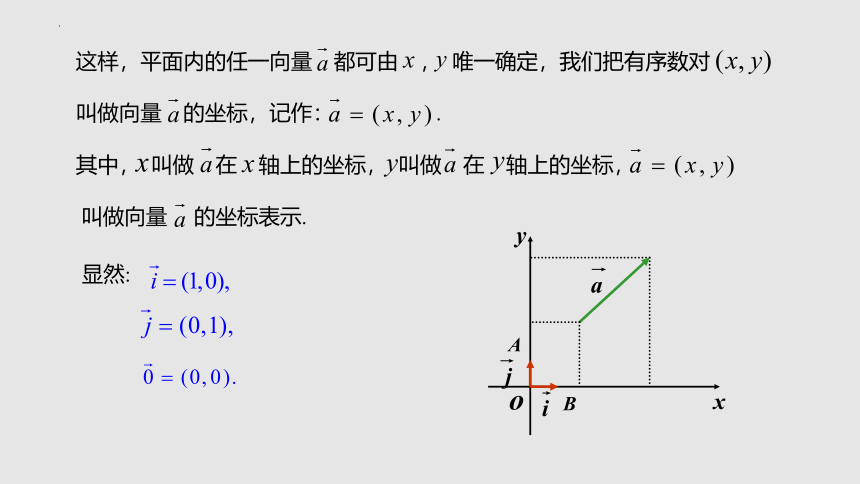
这样,平面内的任一向量 都可由 , 唯一确定,我们把有序数对
叫做向量 的坐标,记作: .
其中, 叫做 在 轴上的坐标, 叫做 在 轴上的坐标,
叫做向量 的坐标表示.
显然:
y
O
x
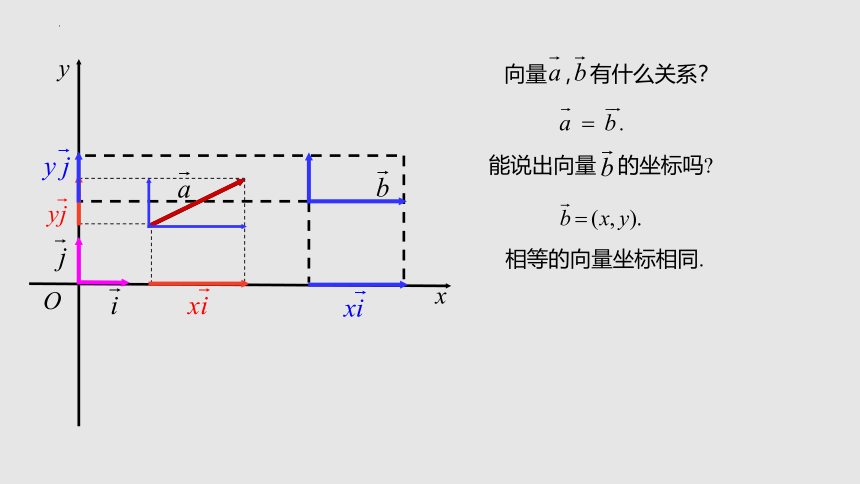
向量 , 有什么关系?
能说出向量 的坐标吗
相等的向量坐标相同.
如图,在直角坐标平面内,以原点 为起点作 ,则点 的位置由 唯一确定.
设 ,则向量 的坐标
就是点 的坐标;
反过来,点 的坐标 也就是向量 的坐标.
因此,在平面直角坐标系内,每一个平面向量都可以用一对实数唯一表示.
练习:在平面直角坐标系内画出下列向量.
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
例1 在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内做直线运动.求出下列位移向量的坐标.
(1)向量 表示沿东北方向移动了2个单位长度;
解:(1)设 ,则
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
例1 在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内做直线运动.求出下列位移向量的坐标.
解:(2)设 ,则
(2)向量 表示沿北偏西 方向移动了3个单位长度;
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
例1 在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内做直线运动.求出下列位移向量的坐标.
解:(1)设 ,则
(3)向量 表示沿南偏东 方向移动了4个单位长度;
思考:已知 ,你能得出 的坐标吗?
两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差).
即
同理可得
思考:已知 ,你能得出 的坐标吗?
即
注:实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
探究:如图,已知 ,你能得出 的坐标吗?
注:一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标.
例2: 已知 , ,求 , 的坐标.
解:
解:
例3: 已知 A(-1,3),B(1,-3),C(4,1),D( 3,4),求向量 , , , 的坐标.
(-1,3),
(1,-3),
(1,-3),
(3,4)-(4,1)=(-1,3) .
例4:如图,已知 的三个顶点 , , 的坐标分别是 ,
, ,求顶点 的坐标.
解法1 设点 的坐标为
所以顶点 的坐标为 .
解法2 由平行四边形法则可得,
而
所以顶点 的坐标为 .
例4:如图,已知 的三个顶点 , , 的坐标分别是 ,
, ,求顶点 的坐标.
练习:已知P1 (x1,y1) ,P2 (x2,y2),P是直线P1 P2 上一点,且 ,求点P的坐标.
解: 设P (x,y) ,则 =(x-x1,y-y1), =(x2-x,y2-y).
由 得
(x-x1,y-y1)= λ (x2-x,y2-y),
于是可得 , .
因此,点P坐标为( , ).
当λ=1时,就得到线段P1P2的中点M坐标公式:
所以中点M 的坐标是( , ) .
总结
1.平面向量的坐标表示:
, 是分别与 轴、 轴方向相同的单位向量,若以 为基底,
则对于平面内任一向量 ,由平面向量基本定理可知,有且只有一对
实数x,y 使得: ,记作:
2.若 ,则:
二、向量数量积的坐标表示
探究:
已知 , ,怎样用 与 的坐标表示 呢?
因为 , ,
所以
又 , , ,
所以 .
这就是说,两个向量的数量积等于它们对应坐标的乘积的和.
向量的模和两点间的距离公式
(1)若 ,则 ,或 .
(2)如果表示向量 的有向线段的起点和终点的坐标分别为 ,
那么: ,
两个向量平行和垂直的坐标表示:
已知 , ,则
两个向量夹角的余弦值的坐标表示:
已知 , ,则
例1.设 , ,求 及 , 的夹角 的余弦值.
解:
因为 , ,
所以
练习 设 , ,求 及 , .
解:
例2.(1)已知定点A和向量 ,点P是直线AB外的一点,请写出点P到直线AB的距离的向量表示.
(2)已知点A(1,1),向量 ,过点A作以向量 为方向向量的直线为l,求点P(3,5)到直线l的距离.
解: (1)设 ,作向量 .
则 表示向量 在向量 上的投影数量,
是点P到直线AB的距离.
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
解: (2)设 ,作向量 .
设 ,
则 ,
令 得 ,
由(1)知, 点P到直线l的距离d= .
课堂小结
1.平面向量数量积的坐标表示:
已知 , ,则 .
2.两个向量平行和垂直的坐标表示:
已知 , ,则
3.两个向量夹角的余弦值的坐标表示:
已知 , ,则
第9章 平面向量
9.3.2 向量坐标表示与运算
在物理中,力是一个向量,力的合成就是向量的加法运算.力也可以分解,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论.
引入
一、向量的坐标表示及坐标运算
平面向量的正交分解:
把一个向量分解为两个互相垂直的向量,叫作把向量正交分解.
如图所示,重力 沿互相垂直的两个方向分解就是正交分解,
重力 可以分解为这样两个分力:平行于斜面使木块沿斜面下
滑的力 ,垂直于斜面的压力 .
正交分解
平面向量的正交分解:
如图,向量 , 是两个互相垂直的单位向量,向量 与 的夹角是30°,
且 ,以向量 , 为一组基,向量 如何表示?
思考:在平面直角坐标系中,每一个点都可用一对有序实数表示,
那么,如何表示直角坐标平面的一个向量呢?
在平面上,如果选取互相垂直的向量作为一组基时,将为我们研究
问题带来方便.
如图, , 是分别与x轴、y轴方向相同的单位向量,若以 为一组基,
则对于平面内任一向量 ,由平面向量基本定理可知,有且只有一对
实数x、y 使得: .
这样,平面内的任一向量 都可由 , 唯一确定,我们把有序数对
叫做向量 的坐标,记作: .
其中, 叫做 在 轴上的坐标, 叫做 在 轴上的坐标,
叫做向量 的坐标表示.
显然:
y
O
x
向量 , 有什么关系?
能说出向量 的坐标吗
相等的向量坐标相同.
如图,在直角坐标平面内,以原点 为起点作 ,则点 的位置由 唯一确定.
设 ,则向量 的坐标
就是点 的坐标;
反过来,点 的坐标 也就是向量 的坐标.
因此,在平面直角坐标系内,每一个平面向量都可以用一对实数唯一表示.
练习:在平面直角坐标系内画出下列向量.
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
例1 在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内做直线运动.求出下列位移向量的坐标.
(1)向量 表示沿东北方向移动了2个单位长度;
解:(1)设 ,则
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
例1 在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内做直线运动.求出下列位移向量的坐标.
解:(2)设 ,则
(2)向量 表示沿北偏西 方向移动了3个单位长度;
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
例1 在平面内,以点O的正东方向为x轴的正向,正北方向为y轴的正向建立平面直角坐标系.质点在平面内做直线运动.求出下列位移向量的坐标.
解:(1)设 ,则
(3)向量 表示沿南偏东 方向移动了4个单位长度;
思考:已知 ,你能得出 的坐标吗?
两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差).
即
同理可得
思考:已知 ,你能得出 的坐标吗?
即
注:实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
探究:如图,已知 ,你能得出 的坐标吗?
注:一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标.
例2: 已知 , ,求 , 的坐标.
解:
解:
例3: 已知 A(-1,3),B(1,-3),C(4,1),D( 3,4),求向量 , , , 的坐标.
(-1,3),
(1,-3),
(1,-3),
(3,4)-(4,1)=(-1,3) .
例4:如图,已知 的三个顶点 , , 的坐标分别是 ,
, ,求顶点 的坐标.
解法1 设点 的坐标为
所以顶点 的坐标为 .
解法2 由平行四边形法则可得,
而
所以顶点 的坐标为 .
例4:如图,已知 的三个顶点 , , 的坐标分别是 ,
, ,求顶点 的坐标.
练习:已知P1 (x1,y1) ,P2 (x2,y2),P是直线P1 P2 上一点,且 ,求点P的坐标.
解: 设P (x,y) ,则 =(x-x1,y-y1), =(x2-x,y2-y).
由 得
(x-x1,y-y1)= λ (x2-x,y2-y),
于是可得 , .
因此,点P坐标为( , ).
当λ=1时,就得到线段P1P2的中点M坐标公式:
所以中点M 的坐标是( , ) .
总结
1.平面向量的坐标表示:
, 是分别与 轴、 轴方向相同的单位向量,若以 为基底,
则对于平面内任一向量 ,由平面向量基本定理可知,有且只有一对
实数x,y 使得: ,记作:
2.若 ,则:
二、向量数量积的坐标表示
探究:
已知 , ,怎样用 与 的坐标表示 呢?
因为 , ,
所以
又 , , ,
所以 .
这就是说,两个向量的数量积等于它们对应坐标的乘积的和.
向量的模和两点间的距离公式
(1)若 ,则 ,或 .
(2)如果表示向量 的有向线段的起点和终点的坐标分别为 ,
那么: ,
两个向量平行和垂直的坐标表示:
已知 , ,则
两个向量夹角的余弦值的坐标表示:
已知 , ,则
例1.设 , ,求 及 , 的夹角 的余弦值.
解:
因为 , ,
所以
练习 设 , ,求 及 , .
解:
例2.(1)已知定点A和向量 ,点P是直线AB外的一点,请写出点P到直线AB的距离的向量表示.
(2)已知点A(1,1),向量 ,过点A作以向量 为方向向量的直线为l,求点P(3,5)到直线l的距离.
解: (1)设 ,作向量 .
则 表示向量 在向量 上的投影数量,
是点P到直线AB的距离.
y
x
O
1 2 3 4
-4 -3 -2 -1
5
4
3
2
1
-1
-2
-3
-4
-5
1 2 3 4
解: (2)设 ,作向量 .
设 ,
则 ,
令 得 ,
由(1)知, 点P到直线l的距离d= .
课堂小结
1.平面向量数量积的坐标表示:
已知 , ,则 .
2.两个向量平行和垂直的坐标表示:
已知 , ,则
3.两个向量夹角的余弦值的坐标表示:
已知 , ,则
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
