山东省潍坊市临朐等八县区2022-2023学年七年级下学期期末考试数学试题(含答案)
文档属性
| 名称 | 山东省潍坊市临朐等八县区2022-2023学年七年级下学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 522.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 20:07:55 | ||
图片预览



文档简介
2022—2023学年度第二学期期末学业质量监测
七年级数学2023.07
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,52分;第Ⅱ卷为非选择题,98分;共150分.考试时间为120分钟.
2.答卷前务必将试题密封线内及答题卡上面的项目填涂清楚.所有答案都必须涂、写在答题卡相应位置,答在本试卷上一律无效.
第Ⅰ卷(选择题,52分)
一、选择题(本题共8小题,每小题4分,共32分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在中,边上的高是()
A. B. C. D.
2.在平面直角坐标系中,已知点P位于第二象限,距离x轴6个单位长度,距离y轴5个单位长度,则点P的坐标是()
A. B. C. D.
3.下列说法错误的是()
A.直径是圆中最长的弦
B.半圆是弧
C.已知圆O的半径为8cm,P为平面内一点,且,则点P在圆O外
D.如果圆A的周长是圆B周长的2倍,那么圆A的面积是圆B面积的2倍
4.已知,则的值为()
A.11 B.25 C.26 D.37
5.如图,将正五边形与正方形按如图所示摆放,公共顶点为O,若点A,B,C,D在同一条直线上,则的度数为()
A.15° B.18° C.28° D.30°
6.已知a,b,c均为常数,若,则的值为()
A.10 B.9 C.8 D.7
7.如图,将直尺与等腰直角三角形叠放在一起,如果,那么的度数为()
A.32° B.48° C.58° D.52°
8.《算法统宗》是一本通俗实用的数学书,也是将数字入诗的代表作,这本书由明代程大位花了近20年完成,程大位还有一首类似二元一次方程组的饮酒数学诗:“肆中饮客乱纷纷,薄酒名脑厚酒醇,醇酒二瓶醉五客,薄酒三瓶醉二人,共同饮了一十六,三十四客醉颜生,试问高明能算士,几多酵酒几多醇 ”这首诗是说,好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒2位客人,如果34位客人醉倒了,他们总共饮下了16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶,依题意,可列方程组为()
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.)
9.下列运算结果正确的是()
A. B.
C. D.
10.如图,在平面直角坐标系中,B,C两点的坐标分别是和,则下列其它各点的坐标正确的是()
A. B. C. D.
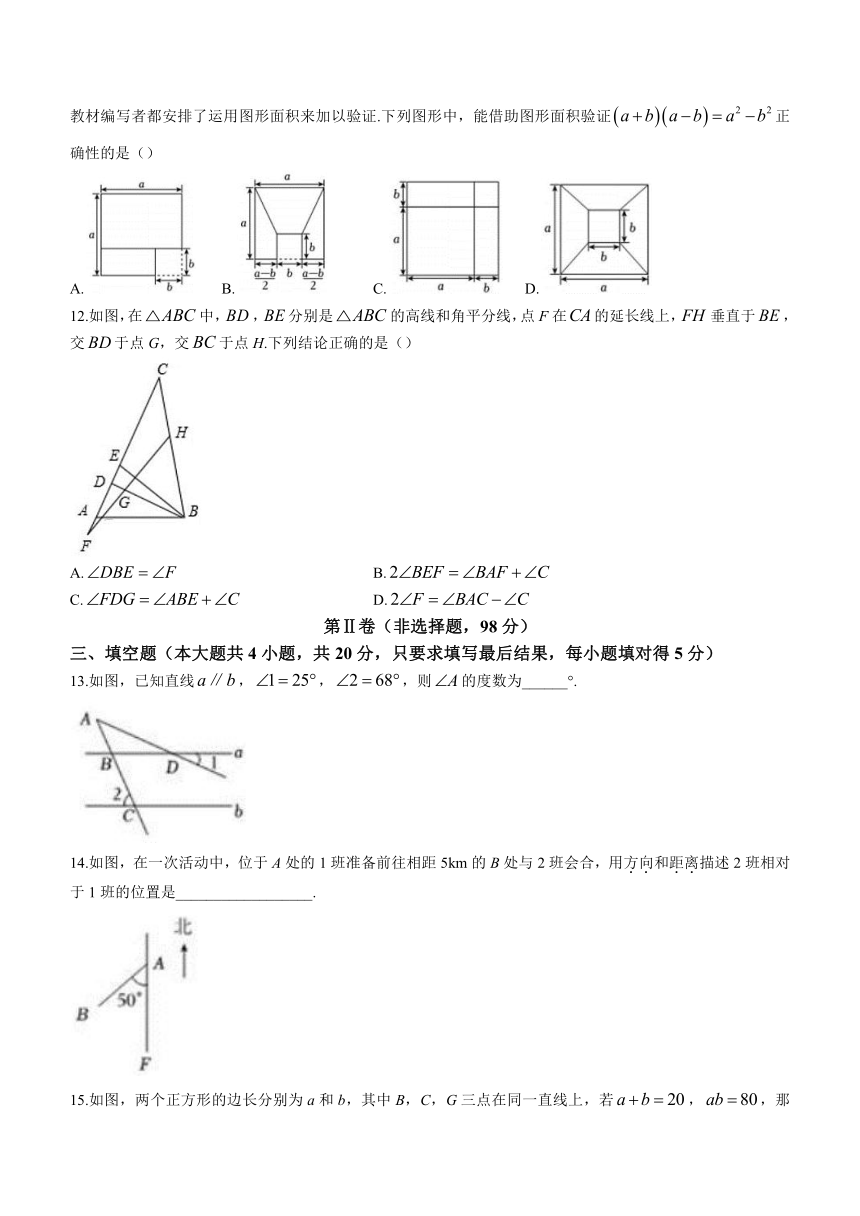
11.数形结合是数学解题中常用的思想方法,数形结合的思想可以使某些抽象的数学问题直观化,生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,每个公式的推导教材编写者都安排了运用图形面积来加以验证.下列图形中,能借助图形面积验证正确性的是()
A. B. C. D.
12.如图,在中,,分别是的高线和角平分线,点F在的延长线上,垂直于,交于点G,交于点H.下列结论正确的是()
A. B.
C. D.
第Ⅱ卷(非选择题,98分)
三、填空题(本大题共4小题,共20分,只要求填写最后结果,每小题填对得5分)
13.如图,已知直线,,,则的度数为______°.
14.如图,在一次活动中,位于A处的1班准备前往相距5km的B处与2班会合,用方向和距离描述2班相对于1班的位置是__________________.
15.如图,两个正方形的边长分别为a和b,其中B,C,G三点在同一直线上,若,,那么阴影部分的面积等于______.
16.中,,,将、按照如图所示折叠,若,则______°.
四、解答题(本大题共7小题,共78分.解答要写出必要的文字说明、证明过程或演算步骤)
17.(本题满分8分)
已知方程组的一个解为,求m,n的值.
18.(本题满分10分)
如图,已知四边形中,点E为上一点,与交于点F,.
(1)若,求的度数;
(2)若,平分,,求的度数.
19.(本题满分15分)因式分解
(1) (2)
(3)
20.(本题满分12分)计算下列各题
(1) (2)
(3)
21.(本题满分10分)
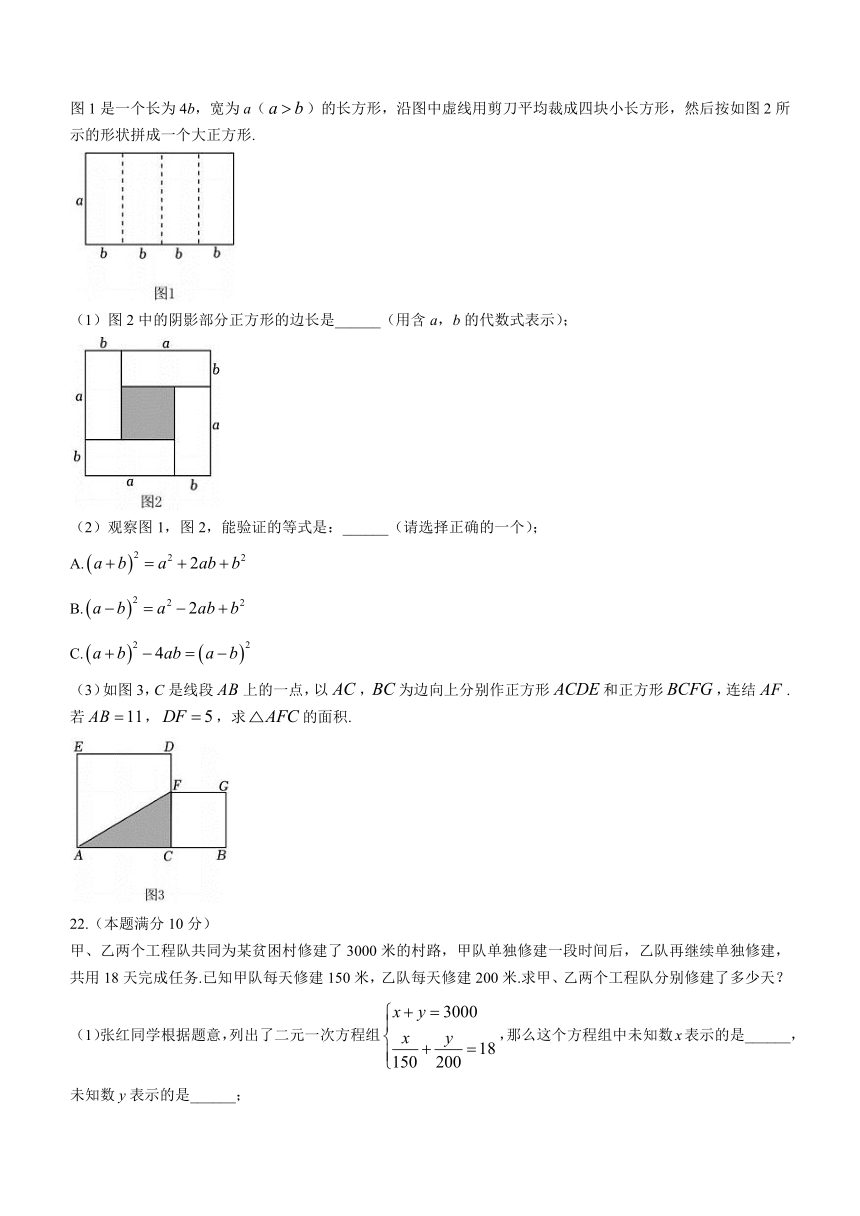
图1是一个长为4b,宽为a()的长方形,沿图中虚线用剪刀平均裁成四块小长方形,然后按如图2所示的形状拼成一个大正方形.
(1)图2中的阴影部分正方形的边长是______(用含a,b的代数式表示);
(2)观察图1,图2,能验证的等式是:______(请选择正确的一个);
A.
B.
C.
(3)如图3,C是线段上的一点,以,为边向上分别作正方形和正方形,连结.若,,求的面积.
22.(本题满分10分)
甲、乙两个工程队共同为某贫困村修建了3000米的村路,甲队单独修建一段时间后,乙队再继续单独修建,共用18天完成任务.已知甲队每天修建150米,乙队每天修建200米.求甲、乙两个工程队分别修建了多少天?
(1)张红同学根据题意,列出了二元一次方程组,那么这个方程组中未知数x表示的是______,未知数y表示的是______;
(2)李芳同学设甲队修建了m天,乙队修建了n天,请你按照她的思路解答老师的问题.
23.(本题满分13分)
【问题背景】(1)已知点,,,,在平面直角坐标系中描出这几个点,并分别找到线段和的中点M,N,然后写出点M和点N的坐标;
【尝试应用】(2)①结合上述结果,我们可以发现:如果线段的两个端点坐标分别为,,则这条线段的中点坐标为____________;
②若点,,用我们发现的结论可以直接得到线段的中点坐标为____________;
【拓展创新】(3)已知三点,,.
①直接写出线段的三等分点的坐标;
②三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,该点叫做三角形的重心.请你写出的重心G的坐标.
2022-2023学年度第二学期期末学业质量监测
七年级数学试题答案及评分标准
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,52分;第Ⅱ卷为非选择题,98分;共150分.考试时间为120分钟.
2.答卷前务必将试题密封线内及答题卡上面的项目填涂清楚.所有答案都必须涂、写在答题卡相应位置,答在本试卷上一律无效.
第Ⅰ卷(选择题,52分)
一、选择题(本题共8小题,每小题4分,共32分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A D A B B C B BC BCD ABD ABD
第Ⅱ卷(非选择题,98分)
三、填空题(本大题共4小题,共20分,只要求填写最后结果,每小题填对得5分)
13.4314.2班在1班的南偏西50°方向上5km处15.12016.265
四、解答题(本大题共7小题,共78分.解答要写出必要的文字说明、证明过程或演算步骤)
17.(本题满分8分)
解:∵是方程组的一个解
∴……3分
解这个方程组得,……3分
答:m,n的值分别是,.……8分
18.(本题满分10分)
解:(1)∵
∴……2分
∴
答:……4分
(2)∵
∴……5分
∵
∴
∴……6分
∴……7分
∵平分
∴
∴……8分
∵,……9分
∴
即……10分
19.(本题满分15分)因式分解:每小题5分。
(1)
……3分
……5分
(2)
……2分
……5分
(3)
……2分
……5分
20.(本题满分12分)计算下列各题:每小题4分。
解:(1)原式……1分
……3分
……4分
(2)原式……2分
……4分
(3)原式……1分
……2分
……3分
……4分
21.(本题满分10分)
解:(1)根据图形可知,图2中的阴影部分的正方形的边长等于,
故答案为:;……2分
(2)由图2知,阴影部分正方形的面积为,
故答案为:C;……5分
(3)设正方形的边长为,正方形的边长为,
∴,,……6分
由(2)知,
∴,
∴,……9分
∴.……10分
22.(本题满分10分)
解:(1)甲工程队共修建的米数,乙工程队共修建的米数;……4分(每空2分)
(2)根据题意得:,……7分
解得;……9分
答:甲工程队修建了12天,乙工程队修建了6天.……10分
23.(本题满分13分)
解:(1)如图,点,,,在平面直角坐标系中描出它们如下:
……2分
线段和中点M、N的坐标分别为,……4分
(2)①线段的中点坐标为……4分
②∵,,
∴由中点坐标公式得,即……8分
(3)线段的三等分点坐标为和……10分
的重心G的坐标为……13分
七年级数学2023.07
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,52分;第Ⅱ卷为非选择题,98分;共150分.考试时间为120分钟.
2.答卷前务必将试题密封线内及答题卡上面的项目填涂清楚.所有答案都必须涂、写在答题卡相应位置,答在本试卷上一律无效.
第Ⅰ卷(选择题,52分)
一、选择题(本题共8小题,每小题4分,共32分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在中,边上的高是()
A. B. C. D.
2.在平面直角坐标系中,已知点P位于第二象限,距离x轴6个单位长度,距离y轴5个单位长度,则点P的坐标是()
A. B. C. D.
3.下列说法错误的是()
A.直径是圆中最长的弦
B.半圆是弧
C.已知圆O的半径为8cm,P为平面内一点,且,则点P在圆O外
D.如果圆A的周长是圆B周长的2倍,那么圆A的面积是圆B面积的2倍
4.已知,则的值为()
A.11 B.25 C.26 D.37
5.如图,将正五边形与正方形按如图所示摆放,公共顶点为O,若点A,B,C,D在同一条直线上,则的度数为()
A.15° B.18° C.28° D.30°
6.已知a,b,c均为常数,若,则的值为()
A.10 B.9 C.8 D.7
7.如图,将直尺与等腰直角三角形叠放在一起,如果,那么的度数为()
A.32° B.48° C.58° D.52°
8.《算法统宗》是一本通俗实用的数学书,也是将数字入诗的代表作,这本书由明代程大位花了近20年完成,程大位还有一首类似二元一次方程组的饮酒数学诗:“肆中饮客乱纷纷,薄酒名脑厚酒醇,醇酒二瓶醉五客,薄酒三瓶醉二人,共同饮了一十六,三十四客醉颜生,试问高明能算士,几多酵酒几多醇 ”这首诗是说,好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒2位客人,如果34位客人醉倒了,他们总共饮下了16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶,依题意,可列方程组为()
A. B. C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.)
9.下列运算结果正确的是()
A. B.
C. D.
10.如图,在平面直角坐标系中,B,C两点的坐标分别是和,则下列其它各点的坐标正确的是()
A. B. C. D.
11.数形结合是数学解题中常用的思想方法,数形结合的思想可以使某些抽象的数学问题直观化,生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,每个公式的推导教材编写者都安排了运用图形面积来加以验证.下列图形中,能借助图形面积验证正确性的是()
A. B. C. D.
12.如图,在中,,分别是的高线和角平分线,点F在的延长线上,垂直于,交于点G,交于点H.下列结论正确的是()
A. B.
C. D.
第Ⅱ卷(非选择题,98分)
三、填空题(本大题共4小题,共20分,只要求填写最后结果,每小题填对得5分)
13.如图,已知直线,,,则的度数为______°.
14.如图,在一次活动中,位于A处的1班准备前往相距5km的B处与2班会合,用方向和距离描述2班相对于1班的位置是__________________.
15.如图,两个正方形的边长分别为a和b,其中B,C,G三点在同一直线上,若,,那么阴影部分的面积等于______.
16.中,,,将、按照如图所示折叠,若,则______°.
四、解答题(本大题共7小题,共78分.解答要写出必要的文字说明、证明过程或演算步骤)
17.(本题满分8分)
已知方程组的一个解为,求m,n的值.
18.(本题满分10分)
如图,已知四边形中,点E为上一点,与交于点F,.
(1)若,求的度数;
(2)若,平分,,求的度数.
19.(本题满分15分)因式分解
(1) (2)
(3)
20.(本题满分12分)计算下列各题
(1) (2)
(3)
21.(本题满分10分)
图1是一个长为4b,宽为a()的长方形,沿图中虚线用剪刀平均裁成四块小长方形,然后按如图2所示的形状拼成一个大正方形.
(1)图2中的阴影部分正方形的边长是______(用含a,b的代数式表示);
(2)观察图1,图2,能验证的等式是:______(请选择正确的一个);
A.
B.
C.
(3)如图3,C是线段上的一点,以,为边向上分别作正方形和正方形,连结.若,,求的面积.
22.(本题满分10分)
甲、乙两个工程队共同为某贫困村修建了3000米的村路,甲队单独修建一段时间后,乙队再继续单独修建,共用18天完成任务.已知甲队每天修建150米,乙队每天修建200米.求甲、乙两个工程队分别修建了多少天?
(1)张红同学根据题意,列出了二元一次方程组,那么这个方程组中未知数x表示的是______,未知数y表示的是______;
(2)李芳同学设甲队修建了m天,乙队修建了n天,请你按照她的思路解答老师的问题.
23.(本题满分13分)
【问题背景】(1)已知点,,,,在平面直角坐标系中描出这几个点,并分别找到线段和的中点M,N,然后写出点M和点N的坐标;
【尝试应用】(2)①结合上述结果,我们可以发现:如果线段的两个端点坐标分别为,,则这条线段的中点坐标为____________;
②若点,,用我们发现的结论可以直接得到线段的中点坐标为____________;
【拓展创新】(3)已知三点,,.
①直接写出线段的三等分点的坐标;
②三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍,该点叫做三角形的重心.请你写出的重心G的坐标.
2022-2023学年度第二学期期末学业质量监测
七年级数学试题答案及评分标准
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,52分;第Ⅱ卷为非选择题,98分;共150分.考试时间为120分钟.
2.答卷前务必将试题密封线内及答题卡上面的项目填涂清楚.所有答案都必须涂、写在答题卡相应位置,答在本试卷上一律无效.
第Ⅰ卷(选择题,52分)
一、选择题(本题共8小题,每小题4分,共32分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A D A B B C B BC BCD ABD ABD
第Ⅱ卷(非选择题,98分)
三、填空题(本大题共4小题,共20分,只要求填写最后结果,每小题填对得5分)
13.4314.2班在1班的南偏西50°方向上5km处15.12016.265
四、解答题(本大题共7小题,共78分.解答要写出必要的文字说明、证明过程或演算步骤)
17.(本题满分8分)
解:∵是方程组的一个解
∴……3分
解这个方程组得,……3分
答:m,n的值分别是,.……8分
18.(本题满分10分)
解:(1)∵
∴……2分
∴
答:……4分
(2)∵
∴……5分
∵
∴
∴……6分
∴……7分
∵平分
∴
∴……8分
∵,……9分
∴
即……10分
19.(本题满分15分)因式分解:每小题5分。
(1)
……3分
……5分
(2)
……2分
……5分
(3)
……2分
……5分
20.(本题满分12分)计算下列各题:每小题4分。
解:(1)原式……1分
……3分
……4分
(2)原式……2分
……4分
(3)原式……1分
……2分
……3分
……4分
21.(本题满分10分)
解:(1)根据图形可知,图2中的阴影部分的正方形的边长等于,
故答案为:;……2分
(2)由图2知,阴影部分正方形的面积为,
故答案为:C;……5分
(3)设正方形的边长为,正方形的边长为,
∴,,……6分
由(2)知,
∴,
∴,……9分
∴.……10分
22.(本题满分10分)
解:(1)甲工程队共修建的米数,乙工程队共修建的米数;……4分(每空2分)
(2)根据题意得:,……7分
解得;……9分
答:甲工程队修建了12天,乙工程队修建了6天.……10分
23.(本题满分13分)
解:(1)如图,点,,,在平面直角坐标系中描出它们如下:
……2分
线段和中点M、N的坐标分别为,……4分
(2)①线段的中点坐标为……4分
②∵,,
∴由中点坐标公式得,即……8分
(3)线段的三等分点坐标为和……10分
的重心G的坐标为……13分
同课章节目录
