正射影和三垂线定理
图片预览




文档简介
课件23张PPT。正射影与三垂线定理(1)你有雄心壮志,我有清华北大复习提问1、直线和平面垂直的定义是什么?
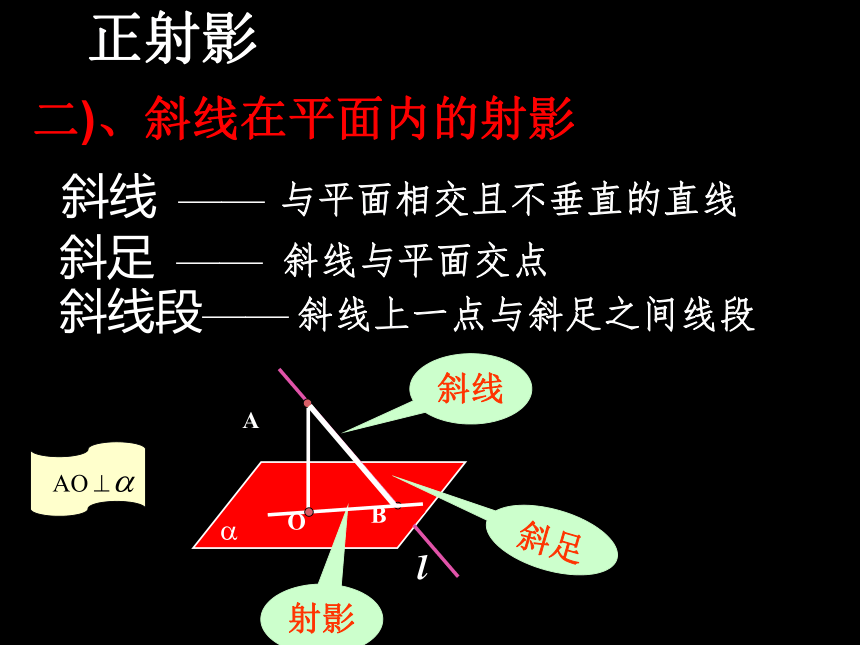
如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,则这条直线和这个平面互相垂直。交点叫做垂足。 如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。2、如何判定直线与平面垂直?一)、点在平面上的射影 垂足P1叫做点P在平面α内的正射影(简称射影)P1Pα正射影 斜线 —— 与平面相交且不垂直的直线
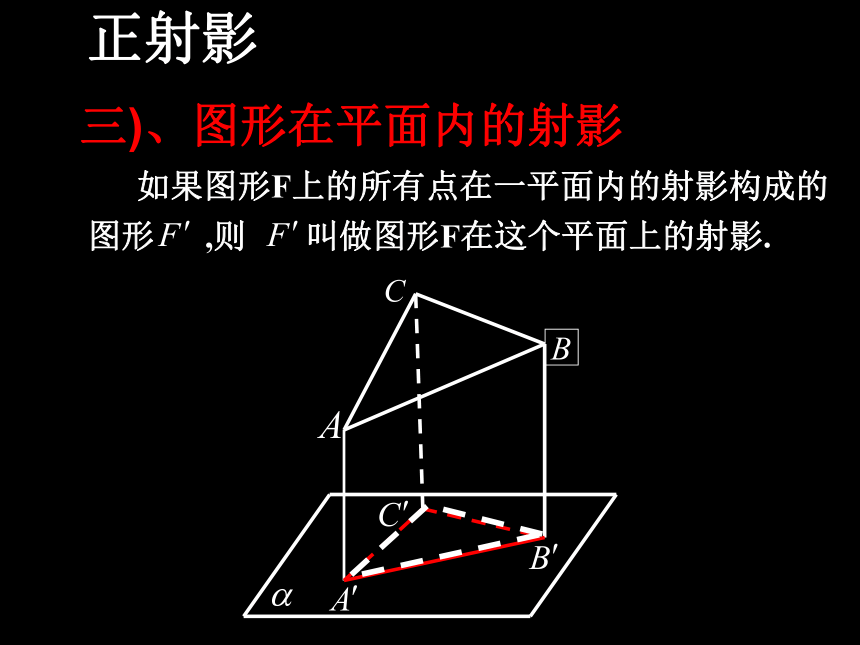
斜足 —— 斜线与平面交点斜线段—— 斜线上一点与斜足之间线段?斜线斜足BAO射影二)、斜线在平面内的射影正射影 如果图形F上的所有点在一平面内的射影构成的图形 ,则 叫做图形F在这个平面上的射影.三)、图形在平面内的射影正射影 思考1:
1)、一条直线在平面内的射影会是怎样的图形?
2)、两条平行直线在平面内的射影是怎样的图形及有怎样的位置关系?
3)、异面直线在平面内的射影是怎样的图形及有怎样的位置关系?
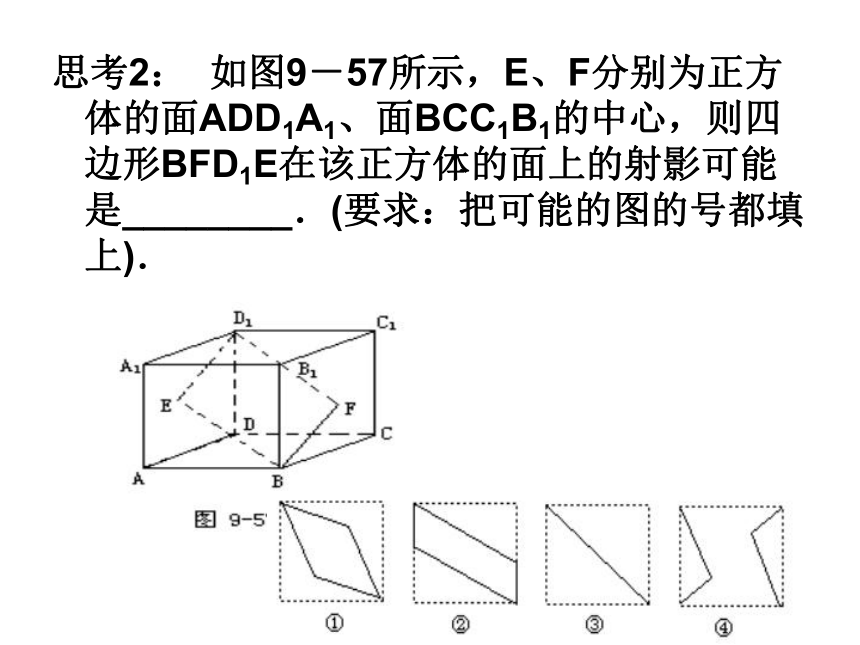
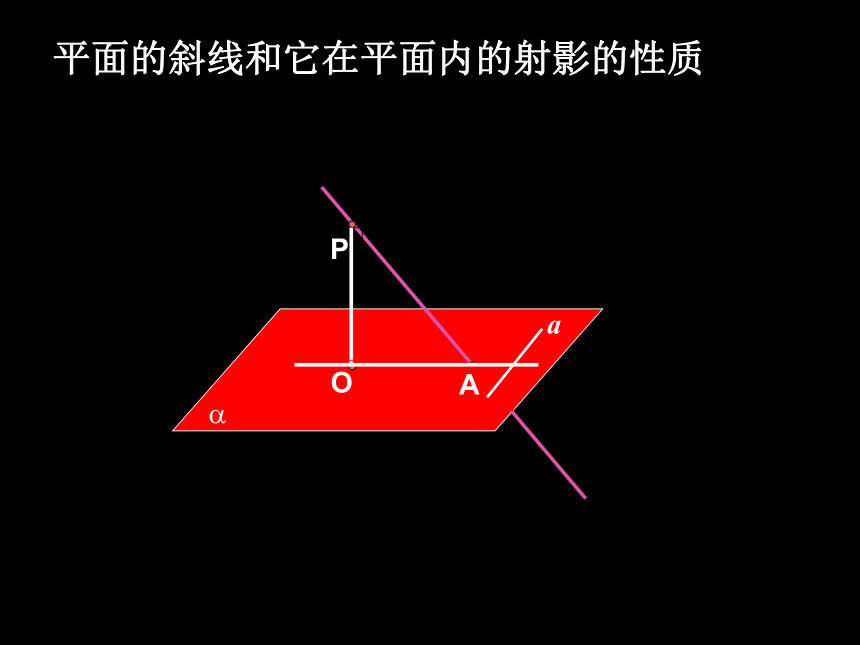
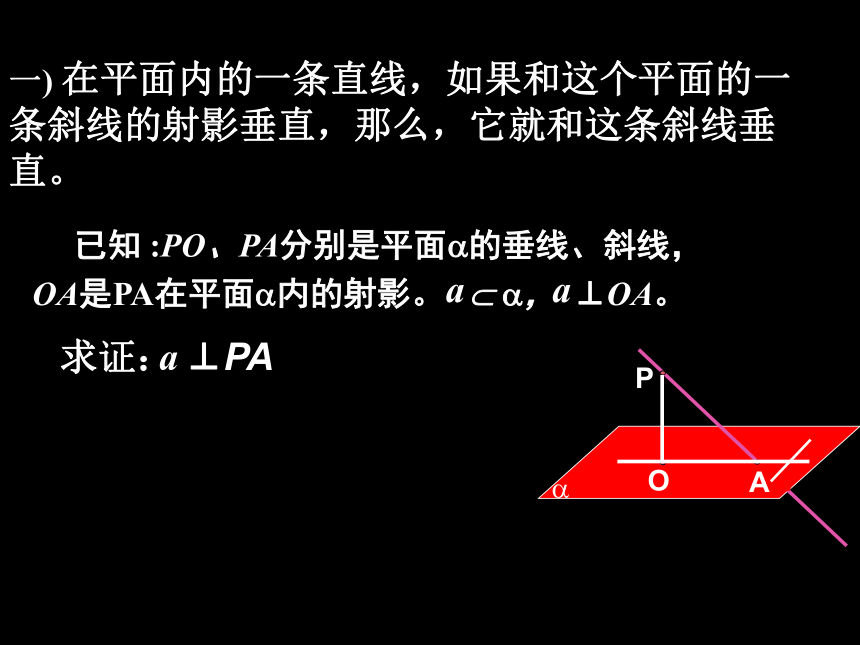
思考2: 如图9-57所示,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是________.(要求:把可能的图的号都填上).PAO?a平面的斜线和它在平面内的射影的性质一) 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。证明:a⊥PAPO⊥?
a ? ?a ⊥ OAa⊥平面PAOPA?平面PAOPO ⊥aPO?OA=O 在平面内的一条直线,如果和这个平面的一条
斜线的射影垂直,那么它就和这条斜线垂直。a
已知 :PO、PA分别是平面?的垂线、斜线,OA是PA在平面?内的射影。 ? ?, 。
a ⊥OA求证:a ⊥PAPO?PA=P三垂线定理线射垂直线斜垂直三垂线定理:
的一条直线和平面的一条斜线在平面内的射影 ,则它就和这条斜线 。三垂线定理的逆定理
平面内的一条直线和平面的一条斜线垂直,则它也和这条斜线的射影垂直。
PAOaα平面内垂直垂直PAOaα三垂线定理是平面的一条斜线与平面内的直线垂直的判定定理,这两条直线可以是: ①相交直线 ②异面直线回顾思考直线a 一定要在平面内,如果 a 不在平面内,定理就不一定成立。注意:如果将定理中
“在平面内”的条件
去掉,结论仍然成立
吗?回顾思考
×⑴若a是平面α的斜线,直线b垂直于
a在平面α内的射影,则 a⊥b ( )⑶若a是平面α的斜线,直线b? α且
b垂直于a在另一平面β内的射影
则a⊥b ( )⑵若 a是平面α的斜线,平面β内 的
直线b垂直于a在平面α内的射 影,
则 a⊥b ( )判断下列命题是否正确:××定理辨析练习:⑷若a是平面α的斜线,b∥α,直线 b垂直
于a在平面α内的射影,则 a⊥b ( ) 问题再现: 1、在正方体ABCD-A1B1C1D1中,求证:A1C⊥平面BDC12.PA⊥平面ABC,AB=AC,M是BC的中点。 求证:BC⊥PM.ABCPM3. PA⊥平面ABC,PB=PC,
M是BC的中点。 求证:AM⊥BC.2.PA⊥平面ABC,AB=AC,M是BC的中点。 求证:BC⊥PM.3. PA⊥平面ABC,PB=PC,
M是BC的中点。 求证:AM⊥BC.ABCPM例1:正方形ABCD 的边长为12,PA⊥平面ABCD,PA=12,O为对角线BD的中点,
求:点P到对角线BD的距离POABCD能力提升:例2、如果一个角所在平面外一点到角的两边距离相等,那么这一点在平面上的射影在这个角的平分线上. 变式1、若ΔABC所在平面α外一点P,且P到三边的距离都相等,则P在α内的射影是三角形的_______。变式2、若ΔABC所在平面α外一点P,且P到三顶点的距离都相等,则P在α内的射影是三角形的_______。问题探索:若ΔABC所在平面α外一点P,且P满足__________,则P在α内的射影是三角形的三角形的垂心。内心外心课堂小结:
1、三垂线定理是研究空间线面位置关系的关键性定理,承上启下,涉及与“垂直”有关的几乎所有领域。2、三垂线定理主要应用于:解决垂直问题与空间图形度量(如角和距离)问题.3、三垂线定理的基本模式导析(1)、一面四线基础平面“一面四线”的不同情况
如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,则这条直线和这个平面互相垂直。交点叫做垂足。 如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。2、如何判定直线与平面垂直?一)、点在平面上的射影 垂足P1叫做点P在平面α内的正射影(简称射影)P1Pα正射影 斜线 —— 与平面相交且不垂直的直线
斜足 —— 斜线与平面交点斜线段—— 斜线上一点与斜足之间线段?斜线斜足BAO射影二)、斜线在平面内的射影正射影 如果图形F上的所有点在一平面内的射影构成的图形 ,则 叫做图形F在这个平面上的射影.三)、图形在平面内的射影正射影 思考1:
1)、一条直线在平面内的射影会是怎样的图形?
2)、两条平行直线在平面内的射影是怎样的图形及有怎样的位置关系?
3)、异面直线在平面内的射影是怎样的图形及有怎样的位置关系?
思考2: 如图9-57所示,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是________.(要求:把可能的图的号都填上).PAO?a平面的斜线和它在平面内的射影的性质一) 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。证明:a⊥PAPO⊥?
a ? ?a ⊥ OAa⊥平面PAOPA?平面PAOPO ⊥aPO?OA=O 在平面内的一条直线,如果和这个平面的一条
斜线的射影垂直,那么它就和这条斜线垂直。a
已知 :PO、PA分别是平面?的垂线、斜线,OA是PA在平面?内的射影。 ? ?, 。
a ⊥OA求证:a ⊥PAPO?PA=P三垂线定理线射垂直线斜垂直三垂线定理:
的一条直线和平面的一条斜线在平面内的射影 ,则它就和这条斜线 。三垂线定理的逆定理
平面内的一条直线和平面的一条斜线垂直,则它也和这条斜线的射影垂直。
PAOaα平面内垂直垂直PAOaα三垂线定理是平面的一条斜线与平面内的直线垂直的判定定理,这两条直线可以是: ①相交直线 ②异面直线回顾思考直线a 一定要在平面内,如果 a 不在平面内,定理就不一定成立。注意:如果将定理中
“在平面内”的条件
去掉,结论仍然成立
吗?回顾思考
×⑴若a是平面α的斜线,直线b垂直于
a在平面α内的射影,则 a⊥b ( )⑶若a是平面α的斜线,直线b? α且
b垂直于a在另一平面β内的射影
则a⊥b ( )⑵若 a是平面α的斜线,平面β内 的
直线b垂直于a在平面α内的射 影,
则 a⊥b ( )判断下列命题是否正确:××定理辨析练习:⑷若a是平面α的斜线,b∥α,直线 b垂直
于a在平面α内的射影,则 a⊥b ( ) 问题再现: 1、在正方体ABCD-A1B1C1D1中,求证:A1C⊥平面BDC12.PA⊥平面ABC,AB=AC,M是BC的中点。 求证:BC⊥PM.ABCPM3. PA⊥平面ABC,PB=PC,
M是BC的中点。 求证:AM⊥BC.2.PA⊥平面ABC,AB=AC,M是BC的中点。 求证:BC⊥PM.3. PA⊥平面ABC,PB=PC,
M是BC的中点。 求证:AM⊥BC.ABCPM例1:正方形ABCD 的边长为12,PA⊥平面ABCD,PA=12,O为对角线BD的中点,
求:点P到对角线BD的距离POABCD能力提升:例2、如果一个角所在平面外一点到角的两边距离相等,那么这一点在平面上的射影在这个角的平分线上. 变式1、若ΔABC所在平面α外一点P,且P到三边的距离都相等,则P在α内的射影是三角形的_______。变式2、若ΔABC所在平面α外一点P,且P到三顶点的距离都相等,则P在α内的射影是三角形的_______。问题探索:若ΔABC所在平面α外一点P,且P满足__________,则P在α内的射影是三角形的三角形的垂心。内心外心课堂小结:
1、三垂线定理是研究空间线面位置关系的关键性定理,承上启下,涉及与“垂直”有关的几乎所有领域。2、三垂线定理主要应用于:解决垂直问题与空间图形度量(如角和距离)问题.3、三垂线定理的基本模式导析(1)、一面四线基础平面“一面四线”的不同情况
