直角三角形的三边关系
图片预览




文档简介
课件12张PPT。
14.1勾股定理 2002年在北京召开了国际数学大会,在那个大会上,到处可以看到一个简洁优美的图案在流动,那个远看象旋转的纸风车的图案就是大会的会标。你知道吗?学习目标1、经历探索勾股定理的过程,培养合情推理能力,体会数形结合的思想。
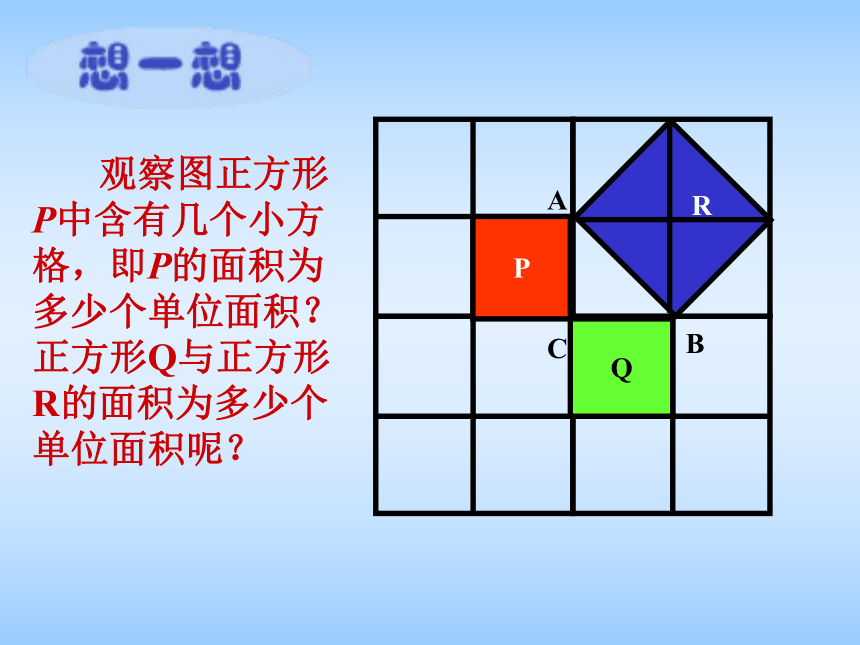
2、能够利用勾股定理解决一些简单的实际问题。猜一猜测量直角三角形纸片的 三边长度,并将各边的长度填入下表:思考:根据测得的数据,你能发现直角三角形三条边长度的平方之间是否存在着一定的关系?你能作出怎样的猜想? 观察图正方形P中含有几个小方格,即P的面积为多少个单位面积?正方形Q与正方形R的面积为多少个单位面积呢?
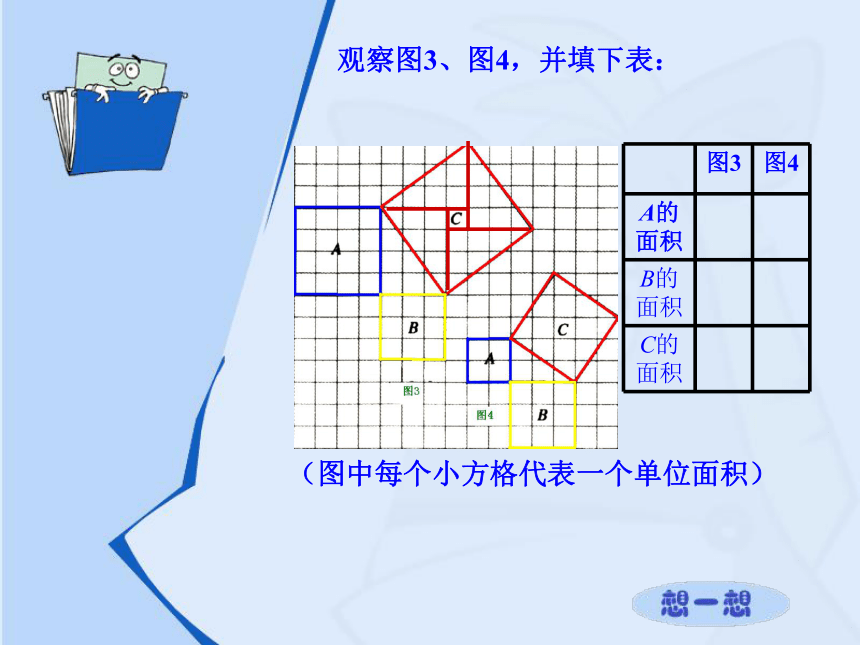
(图中每个小方格代表一个单位面积)观察图3、图4,并填下表: 三个正方形A、B、C的面积之间存在什么关系?
那么,你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流。对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么 a2+b2 =c2
勾股定理:直角三角形两直角边的
平方和 等于斜边的平方 记一记 例题: 将长为13米的梯子AC斜靠在墙
上,BC长为5米,求梯子上端A到墙的
底端B的距离AB。CA B试一试学以致用 如图,为了求出位于湖两岸的两点A、B之间的距离,一个观测者在点C设桩,使三角形ABC恰为直角三角形。通过测量,得到AC长160米,BC长128米。问从点A穿过湖到点B有多远?BCA160m128m说一说 本节课你的收获是什么?(先小组内讨论交流,然后全班汇报。)请各位老师指导
2、能够利用勾股定理解决一些简单的实际问题。猜一猜测量直角三角形纸片的 三边长度,并将各边的长度填入下表:思考:根据测得的数据,你能发现直角三角形三条边长度的平方之间是否存在着一定的关系?你能作出怎样的猜想? 观察图正方形P中含有几个小方格,即P的面积为多少个单位面积?正方形Q与正方形R的面积为多少个单位面积呢?
(图中每个小方格代表一个单位面积)观察图3、图4,并填下表: 三个正方形A、B、C的面积之间存在什么关系?
那么,你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流。对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么 a2+b2 =c2
勾股定理:直角三角形两直角边的
平方和 等于斜边的平方 记一记 例题: 将长为13米的梯子AC斜靠在墙
上,BC长为5米,求梯子上端A到墙的
底端B的距离AB。CA B试一试学以致用 如图,为了求出位于湖两岸的两点A、B之间的距离,一个观测者在点C设桩,使三角形ABC恰为直角三角形。通过测量,得到AC长160米,BC长128米。问从点A穿过湖到点B有多远?BCA160m128m说一说 本节课你的收获是什么?(先小组内讨论交流,然后全班汇报。)请各位老师指导
