二次函数复习
图片预览





文档简介
课件27张PPT。二 次 函 数
复习课GO绍兴县孙端镇中学 初三数学备课组一、知识梳理
二、练习巩固
三、中考链接
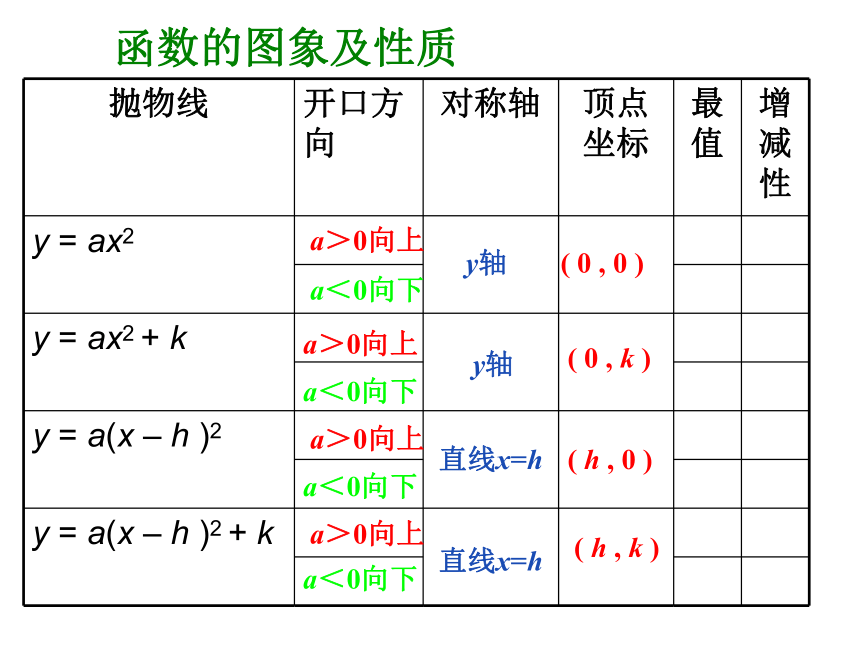
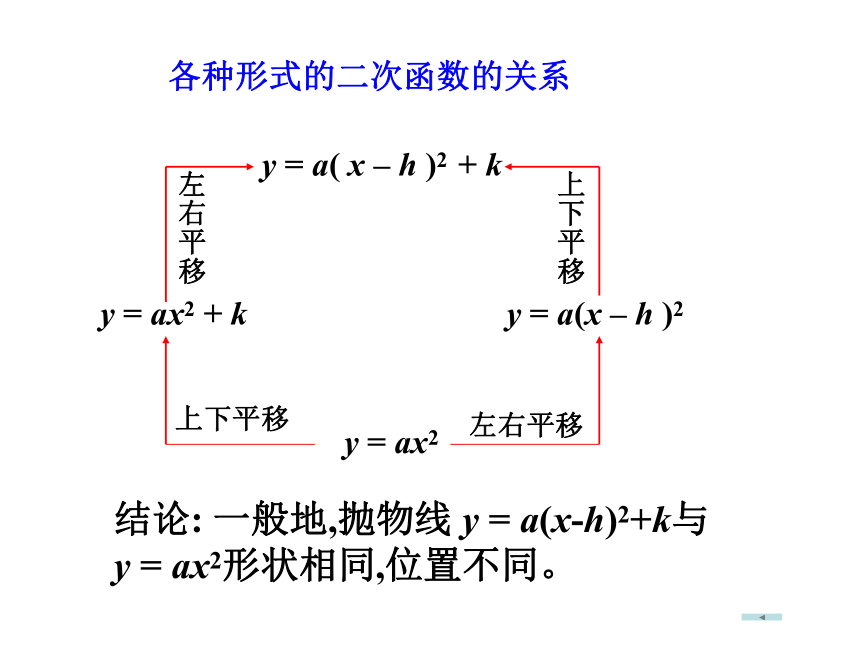
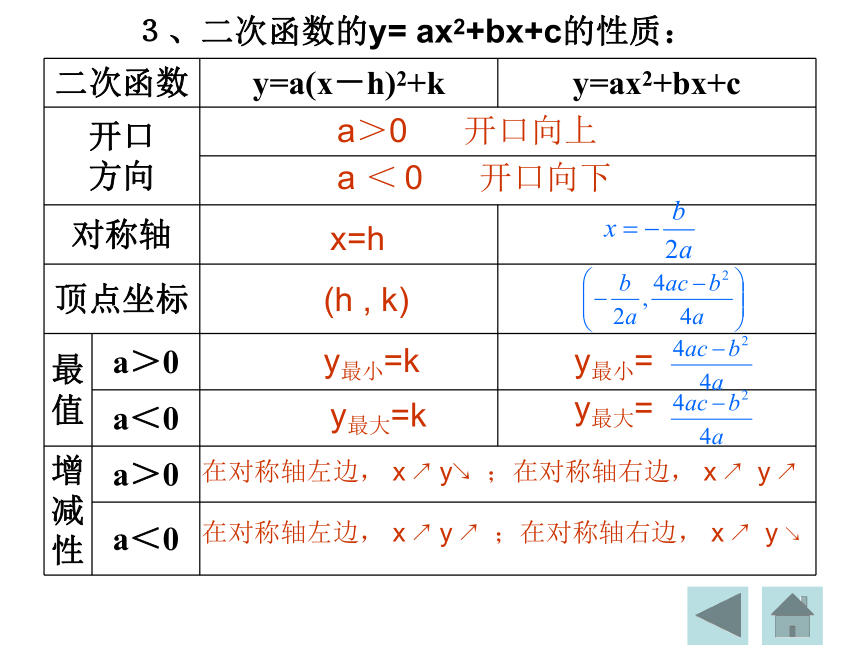
四、课堂小结知识梳理: 1、二次函数的概念:函数y= (a、b、c为常数,______)叫做二次函数。ax2+bx+ca ≠0 2、二次函数的图象是一条 。 抛物线函数的图象及性质a>0向上a<0向下a>0向上a>0向上a>0向上a<0向下a<0向下a<0向下y轴直线x=h直线x=hy轴( 0 , 0 )( 0 , k )( h , 0 )( h , k )y = ax2y = ax2 + k y = a(x – h )2y = a( x – h )2 + k上下平移左右平移上下平移左右平移结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。各种形式的二次函数的关系 3、二次函数的y= ax2+bx+c的性质:a>0 开口向上a < 0 开口向下x=h(h , k)y最小=ky最大=ky最小=y最大=在对称轴左边, x ↗y↘ ;在对称轴右边, x ↗ y ↗ 在对称轴左边, x ↗y ↗ ;在对称轴右边, x ↗ y ↘ 同学们,你们已经学习过二次函数,请你画出二次函数y=-x2-2x+3的图象,根据图
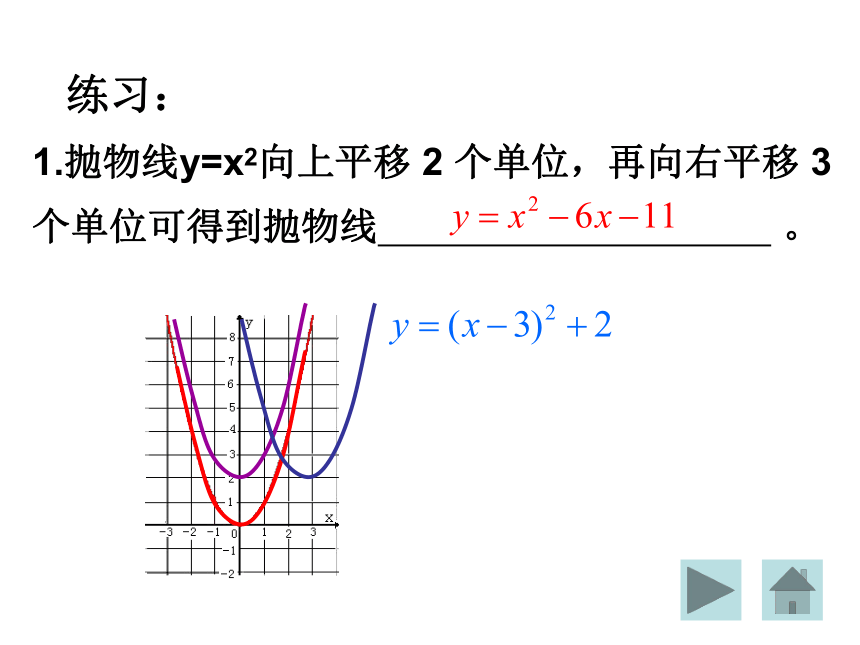
象、结合函数的解析式,你能说出哪些结论?练习:1.抛物线y=x2向上平移 2 个单位,再向右平移 3 个单位可得到抛物线 。已知抛物线y=-x2-2x+m.(2)若抛物线与y轴交于正半轴,则m______0; (填“>”、“=”或“<”)(1)若抛物线经过坐标系原点,则m______0; (填“>”、“=”或“<”)(4)若抛物线与x轴有两个交点,则m______。(3)若抛物线与x轴有一个交点,则m_______.>=>-1=-1练习:2.将函数y= x2+6x+7进行配方正确的结果应为( )C练习:3.抛物线的图像如下,则满足条件a>0, b<0, c<0的是( )
ADCBD4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:① abc>0 ;② b2-4ac<0;③ b+2a<0;④ a+b+c>0. 其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②③a<0,b>0,c>0练习:A练习:5.二次函数y= ax2+bx+c的图象如图所示,求此函数解析式。-632-2(1)方法一 (一般式)方法二 (顶点式)方法三 (交点式)(2)知识拓展一般式:
解:依题意把点(2,0)(-6,0)(0,3) 可得:
4a+2b+c=0
c=3
36a-6b+c=0
解得: a=
b= -1
c=3
所以二次函数的解析式为:顶点式:
解:因为二次函数的对称轴为x=-2,所以可设函数的解析式为:y=a(x+2)2+k,把点(2,0)(0,3)代入可得:
16a+k=0
4a+k=3
解得 a=
k=4
所以二次函数的解析式为:交点式:
解:因为抛物线与x轴相交的两个点的坐标为(2,0)(-6,0),可设该函数的解析式为:y=a(x+6)(x-2),把点(0,3)代入得:
3= -12a
解得:a=
所以二次函数的解析式为:
拓展:
若抛物线y1 = a1x2+b1x+c1与以上抛物线关于x轴对称,试求y1 = a1x2+b1x+c1的解析式。6.二次函数y= ax2+bx+c的图象如图所示,求此函数解析式。练习:中考链接:1.(北京)如果b>0,c>0,那么二次函数的图象大致是(??? )
????????????? A.????????? ? B.?????????? C.?????????????? D.
D中考链接:2.(05浙江丽水)如图,抛物线的顶点P的坐标是(1,-3),则此抛物线对应的二次函数有( )
(A)最大值1
(B)最小值-3
(C)最大值-3
(D)最小值1B中考链接:3.(05常州)已知抛物线的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线向 平移 个单位,则得到抛物线 31<X<5下1中考链接:4.(05梅州)根据图1中的抛物线,
当x 时,y随x的增大而增大,
当x 时,y随x的增大而减小,
当x 时,y有最大值。<2>2=25.(05河南)如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积是 。 中考链接:中考链接:6.(05十堰)张大伯准备用40m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形的羊圈。
请你求出张大伯矩形羊圈的面积;
请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由。练习:7.如图,隧道的截面由抛物线AED和矩形ABCD组成,矩形的长BC为8米,宽AB为2米,以BC所在的直线为x轴,以BC的中垂线为y轴,建立直角坐标系。y轴是抛物线的对称轴,顶点E到坐标原点的距离为6米。
(1)求抛物线的解析式;
(2)现有一货车卡高4.2米,宽
2.4米,这辆车能否通过该隧道?
请说明理由。
(3)若该隧道内设双行道,
该辆车还能通过隧道吗?请说明理由。
GOGO(2)现有一货车卡高4.2米,宽2.4米,这辆车能否通过该隧道?请说明理由。 解:
把x=1.2代入 中,解得y=5.64。
∵4.2<5.64
∴这辆车能通过该隧道(3)若该隧道内设双行道,现有一货车卡高4.2米,宽2.4米,这辆车能否通过该隧道?请说明理由。 解:
把x=2.4代入 中,解得y =4.56。
∵4.2<4.56
∴这辆车能通过该隧道课堂小结:1、二次函数的概念:
二次函数的概念:函数y= (a、b、c为常数,其中 )叫做二次函数。
2、二次函数的图象:
二次函数的图象是一条抛物线。
3、二次函数的性质:
包括抛物线的三要素,最值,增减性。
4、二次函数的实践应用(数形结合)
具体体现在解决一些实际应用题中。ax2+bx+ca ≠0
二、练习巩固
三、中考链接
四、课堂小结知识梳理: 1、二次函数的概念:函数y= (a、b、c为常数,______)叫做二次函数。ax2+bx+ca ≠0 2、二次函数的图象是一条 。 抛物线函数的图象及性质a>0向上a<0向下a>0向上a>0向上a>0向上a<0向下a<0向下a<0向下y轴直线x=h直线x=hy轴( 0 , 0 )( 0 , k )( h , 0 )( h , k )y = ax2y = ax2 + k y = a(x – h )2y = a( x – h )2 + k上下平移左右平移上下平移左右平移结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。各种形式的二次函数的关系 3、二次函数的y= ax2+bx+c的性质:a>0 开口向上a < 0 开口向下x=h(h , k)y最小=ky最大=ky最小=y最大=在对称轴左边, x ↗y↘ ;在对称轴右边, x ↗ y ↗ 在对称轴左边, x ↗y ↗ ;在对称轴右边, x ↗ y ↘ 同学们,你们已经学习过二次函数,请你画出二次函数y=-x2-2x+3的图象,根据图
象、结合函数的解析式,你能说出哪些结论?练习:1.抛物线y=x2向上平移 2 个单位,再向右平移 3 个单位可得到抛物线 。已知抛物线y=-x2-2x+m.(2)若抛物线与y轴交于正半轴,则m______0; (填“>”、“=”或“<”)(1)若抛物线经过坐标系原点,则m______0; (填“>”、“=”或“<”)(4)若抛物线与x轴有两个交点,则m______。(3)若抛物线与x轴有一个交点,则m_______.>=>-1=-1练习:2.将函数y= x2+6x+7进行配方正确的结果应为( )C练习:3.抛物线的图像如下,则满足条件a>0, b<0, c<0的是( )
ADCBD4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:① abc>0 ;② b2-4ac<0;③ b+2a<0;④ a+b+c>0. 其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②③a<0,b>0,c>0练习:A练习:5.二次函数y= ax2+bx+c的图象如图所示,求此函数解析式。-632-2(1)方法一 (一般式)方法二 (顶点式)方法三 (交点式)(2)知识拓展一般式:
解:依题意把点(2,0)(-6,0)(0,3) 可得:
4a+2b+c=0
c=3
36a-6b+c=0
解得: a=
b= -1
c=3
所以二次函数的解析式为:顶点式:
解:因为二次函数的对称轴为x=-2,所以可设函数的解析式为:y=a(x+2)2+k,把点(2,0)(0,3)代入可得:
16a+k=0
4a+k=3
解得 a=
k=4
所以二次函数的解析式为:交点式:
解:因为抛物线与x轴相交的两个点的坐标为(2,0)(-6,0),可设该函数的解析式为:y=a(x+6)(x-2),把点(0,3)代入得:
3= -12a
解得:a=
所以二次函数的解析式为:
拓展:
若抛物线y1 = a1x2+b1x+c1与以上抛物线关于x轴对称,试求y1 = a1x2+b1x+c1的解析式。6.二次函数y= ax2+bx+c的图象如图所示,求此函数解析式。练习:中考链接:1.(北京)如果b>0,c>0,那么二次函数的图象大致是(??? )
????????????? A.????????? ? B.?????????? C.?????????????? D.
D中考链接:2.(05浙江丽水)如图,抛物线的顶点P的坐标是(1,-3),则此抛物线对应的二次函数有( )
(A)最大值1
(B)最小值-3
(C)最大值-3
(D)最小值1B中考链接:3.(05常州)已知抛物线的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线向 平移 个单位,则得到抛物线 31<X<5下1中考链接:4.(05梅州)根据图1中的抛物线,
当x 时,y随x的增大而增大,
当x 时,y随x的增大而减小,
当x 时,y有最大值。<2>2=25.(05河南)如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C、E和点D、F,则图中阴影部分的面积是 。 中考链接:中考链接:6.(05十堰)张大伯准备用40m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形的羊圈。
请你求出张大伯矩形羊圈的面积;
请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由。练习:7.如图,隧道的截面由抛物线AED和矩形ABCD组成,矩形的长BC为8米,宽AB为2米,以BC所在的直线为x轴,以BC的中垂线为y轴,建立直角坐标系。y轴是抛物线的对称轴,顶点E到坐标原点的距离为6米。
(1)求抛物线的解析式;
(2)现有一货车卡高4.2米,宽
2.4米,这辆车能否通过该隧道?
请说明理由。
(3)若该隧道内设双行道,
该辆车还能通过隧道吗?请说明理由。
GOGO(2)现有一货车卡高4.2米,宽2.4米,这辆车能否通过该隧道?请说明理由。 解:
把x=1.2代入 中,解得y=5.64。
∵4.2<5.64
∴这辆车能通过该隧道(3)若该隧道内设双行道,现有一货车卡高4.2米,宽2.4米,这辆车能否通过该隧道?请说明理由。 解:
把x=2.4代入 中,解得y =4.56。
∵4.2<4.56
∴这辆车能通过该隧道课堂小结:1、二次函数的概念:
二次函数的概念:函数y= (a、b、c为常数,其中 )叫做二次函数。
2、二次函数的图象:
二次函数的图象是一条抛物线。
3、二次函数的性质:
包括抛物线的三要素,最值,增减性。
4、二次函数的实践应用(数形结合)
具体体现在解决一些实际应用题中。ax2+bx+ca ≠0
