三.圆的周长与面积18、扇形同步练习 浙教版六年级上册数学(含答案)
文档属性
| 名称 | 三.圆的周长与面积18、扇形同步练习 浙教版六年级上册数学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览



文档简介
三.圆的周长与面积18、扇形同步练习 含答案
浙教版六年级上册数学
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.顶点在( )的角叫圆心角。
2.一条弧和经过这条弧两端的半径所围成的图形叫做( )。
3.在一个圆上,任意画出三条半径,可以在此图中找出( )个扇形。
4.把一张半径3厘米的圆形彩纸对折剪成两个半圆,两个半圆的周长和比原来圆的周长多( )厘米,两个半圆的面积和是( )平方厘米。
5.圈心角是的扇形的面积是整个圆面积的( )。(填分数)
6.扇形的周长包括一段( )的长度和两条( )的长度。
7.在同一个圆中,扇形的大小与这个扇形的( )的大小有关。
8.如图,在长方形ABCD中,AB=6厘米,AD=8厘米,对角线BD=10厘米,阴影部分的面积是( )。
9.如图,长方形的周长是( ),面积是( )。
二、选择题
10.扇形是( )图形.
A.轴对称 B.平移 C.旋转
11.下面各个图形的阴影部分扇形的是( ).
A. B. C.
12.扇形有( )对称轴。
A.无数条 B.一条 C.没有
三、判断题
13.两个扇形中,圆心角大的扇形面积就大。( )
14.圆的一部分就是扇形。( )
15.扇形有无数条对称轴。( )
16.四个半径相等的扇形可以组成一个圆形。( )
17.扇形是由两条半径和圆上的一段曲线围成。( )
四、计算
18.求下列阴影部分的面积。
五、解答题
19.半径为6厘米的扇形面积为18.84平方厘米,它的圆心角是多少度?
20.画一个直径是12厘米的圆,并在圆中画一个圆心角是100°的扇形。求这个扇形的面积。
21.有一片正方形草地(如图),一只羊拴在正方形草地的一角的木桩上,拴羊的绳子正好等于正方形草地的边长。已知这只羊能吃到草部分的周长是6.28米,求这只羊吃不到草部分的面积(π=3.14)
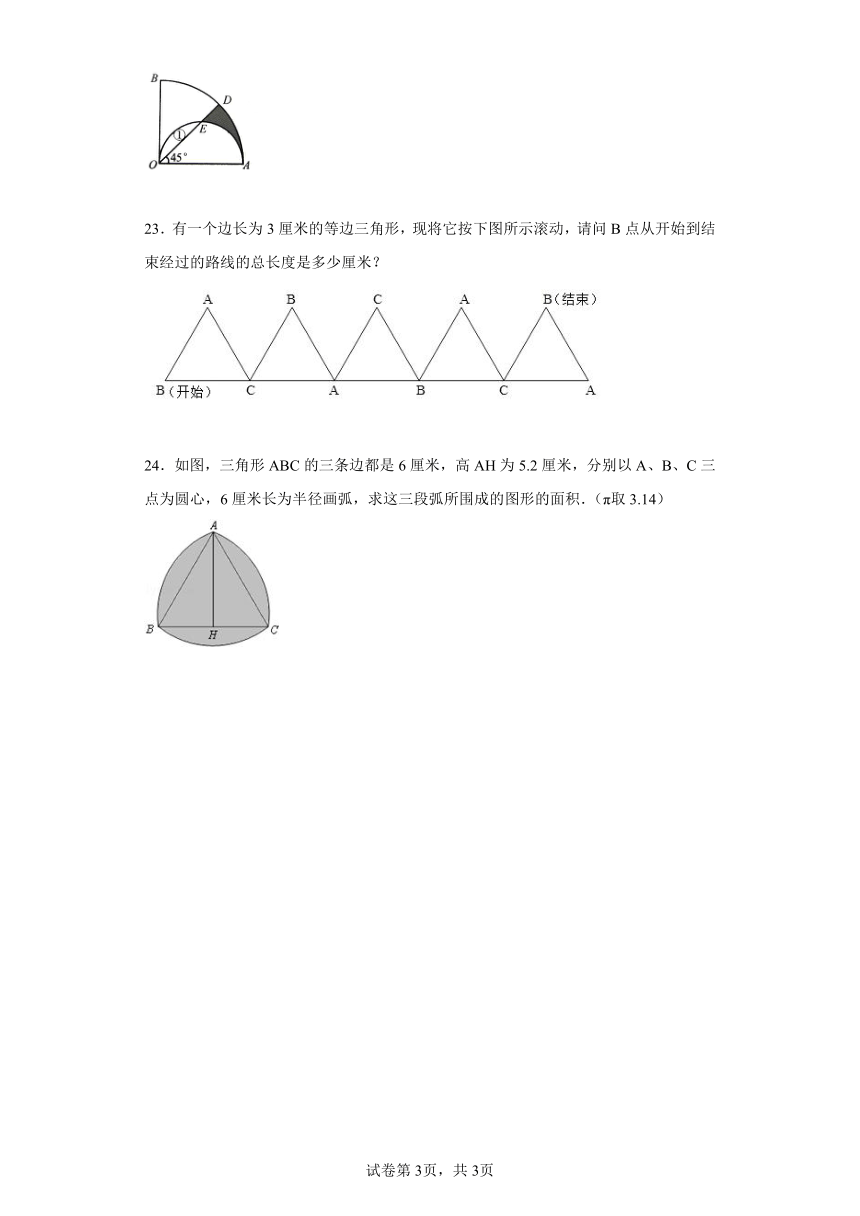
22.下图中,∠BOA=90°,以AO为直径画半圆交OD于E,如果图中①的面积为1平方厘米,求阴影部分的面积.
23.有一个边长为3厘米的等边三角形,现将它按下图所示滚动,请问B点从开始到结束经过的路线的总长度是多少厘米?
24.如图,三角形ABC的三条边都是6厘米,高AH为5.2厘米,分别以A、B、C三点为圆心,6厘米长为半径画弧,求这三段弧所围成的图形的面积.(π取3.14)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.圆心上
2.扇形
3.6
4.12 28.26
5.
6.弧 半径
7.圆心角
8.30.5平方厘米
观察图形可知,扇形的半径等于长方形的一条对角线(AC)的长度,即是10厘米,所以阴影部分的面积等于这个半径10厘米的扇形的面积与这个长方形的面积之差,据此利用圆的面积公式和长方形的面积公式计算即可解答。
3.14×10 ÷4-6×8
=314÷4-48
=78.5-48
=30.5(平方厘米)
答:阴影部分的面积是30.5平方厘米。
9.
根据图意可知长方形的宽是3厘米,因为长方形里面画的是2个四分之一圆,那么长方形的长是宽的2倍。
长方形的宽为圆的半径,长为两条圆的半径,故长方形的长为3×2=6(厘米)。长方形的周长为3+6=9(厘米),9×2=18(厘米),面积为:3×6=18(平方厘米)。
10.A
11.A
12.B
13.×
14.×
15.×
16.×
17.√
18.根据第一个图可知,阴影部分面积=半圆的面积-三角形的面积,根据半圆的面积公式:S=πr2÷2,三角形的面积公式:底×高÷2,把数代入即可求解。
根据第二个图可知,阴影部分面积=正方形的面积-圆的面积,根据圆的面积公式:πr2×,正方形的面积公式:边长×边长,把数代入即可求解。
三角形面积:12×4÷2
=48÷2
=24(cm2)
半圆面积:3.14×(12÷2)2÷2
=3.14×36÷2
=113.04÷2
=56.52(cm2)
阴影部分面积:56.52-24=32.52(cm2);
正方形面积:8×8=64(cm2)
圆的面积: 3.14×8×8×
=25.12×8×
=50.24(cm2)
阴影部分面积:64-50.24=13.76(cm2)
19.3.14×6×6=113.04(平方厘米)
18.84÷113.04×360=60(度)
答:它的圆心角是60度.
20.圆心角是100度,用100除以360求出圆心角占360度的几分之几,那么扇形面积就占所在圆面积的几分之几.
12÷2=6(厘米)
3.14×6×6=113.04(平方厘米)
113.04×=31.4(平方厘米)
答:这个扇形的面积是31.4平方厘米.
21.试题分析:由题意可知:这只羊能吃到的草的部分是一个以正方形的边长为半径的圆,其周长已知,于是可以求出其半径,进而依据“吃不到的面积=正方形的面积﹣吃到草的面积”,据此代入数据即可求解.
解:设正方形的边长为a,
则2a+×2×3.14×a=6.28,
2a+1.57a=6.28,
3.57a=6.28,
a=,
﹣,
=0.215×,
≈0.7(平方米);
答:这只羊吃不到草部分的面积约是0.7平方米。
22.设OA=2r
因为,∠BOA=90°,所以,S扇形AOB=,
又因为∠AOD=45°,所以S扇形AOD=S扇形AOB=πr2,
S半圆=πr2,
所以:S阴影=图中①的面积=1平方厘米
23.3.14×3×2÷360°×120°×3
=9.42×2÷360°×120°×3
=18.84÷360°×120°×3
=18.84(厘米)
答:B点从开始到结束经过的路线的总长度是18.84厘米.
24.根据题干三角形ABC是等边三角形,所以每个角的度数都是60°,那么图中就出现了3个半径为6厘米,圆心角为60°的扇形;这三段弧所围成的图形的面积=三个扇形的面积之和﹣2个等边三角形的面积,由此利用扇形的面积公式和三角形的面积公式即可解决问题.
解:一个小扇形的面积是:×3.14×62,
=×3.14×36,
=18.84(平方厘米),
等边三角形的面积为:6×5.2÷2=15.6(平方厘米),
所以这三段弧所围成的图形的面积是:18.84×3﹣15.6×2=56.52﹣31.2=25.32(平方厘米),
答:这三段弧所围成的图形的面积是25.32平方厘米。
答案第1页,共2页
答案第1页,共2页
浙教版六年级上册数学
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.顶点在( )的角叫圆心角。
2.一条弧和经过这条弧两端的半径所围成的图形叫做( )。
3.在一个圆上,任意画出三条半径,可以在此图中找出( )个扇形。
4.把一张半径3厘米的圆形彩纸对折剪成两个半圆,两个半圆的周长和比原来圆的周长多( )厘米,两个半圆的面积和是( )平方厘米。
5.圈心角是的扇形的面积是整个圆面积的( )。(填分数)
6.扇形的周长包括一段( )的长度和两条( )的长度。
7.在同一个圆中,扇形的大小与这个扇形的( )的大小有关。
8.如图,在长方形ABCD中,AB=6厘米,AD=8厘米,对角线BD=10厘米,阴影部分的面积是( )。
9.如图,长方形的周长是( ),面积是( )。
二、选择题
10.扇形是( )图形.
A.轴对称 B.平移 C.旋转
11.下面各个图形的阴影部分扇形的是( ).
A. B. C.
12.扇形有( )对称轴。
A.无数条 B.一条 C.没有
三、判断题
13.两个扇形中,圆心角大的扇形面积就大。( )
14.圆的一部分就是扇形。( )
15.扇形有无数条对称轴。( )
16.四个半径相等的扇形可以组成一个圆形。( )
17.扇形是由两条半径和圆上的一段曲线围成。( )
四、计算
18.求下列阴影部分的面积。
五、解答题
19.半径为6厘米的扇形面积为18.84平方厘米,它的圆心角是多少度?
20.画一个直径是12厘米的圆,并在圆中画一个圆心角是100°的扇形。求这个扇形的面积。
21.有一片正方形草地(如图),一只羊拴在正方形草地的一角的木桩上,拴羊的绳子正好等于正方形草地的边长。已知这只羊能吃到草部分的周长是6.28米,求这只羊吃不到草部分的面积(π=3.14)
22.下图中,∠BOA=90°,以AO为直径画半圆交OD于E,如果图中①的面积为1平方厘米,求阴影部分的面积.
23.有一个边长为3厘米的等边三角形,现将它按下图所示滚动,请问B点从开始到结束经过的路线的总长度是多少厘米?
24.如图,三角形ABC的三条边都是6厘米,高AH为5.2厘米,分别以A、B、C三点为圆心,6厘米长为半径画弧,求这三段弧所围成的图形的面积.(π取3.14)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.圆心上
2.扇形
3.6
4.12 28.26
5.
6.弧 半径
7.圆心角
8.30.5平方厘米
观察图形可知,扇形的半径等于长方形的一条对角线(AC)的长度,即是10厘米,所以阴影部分的面积等于这个半径10厘米的扇形的面积与这个长方形的面积之差,据此利用圆的面积公式和长方形的面积公式计算即可解答。
3.14×10 ÷4-6×8
=314÷4-48
=78.5-48
=30.5(平方厘米)
答:阴影部分的面积是30.5平方厘米。
9.
根据图意可知长方形的宽是3厘米,因为长方形里面画的是2个四分之一圆,那么长方形的长是宽的2倍。
长方形的宽为圆的半径,长为两条圆的半径,故长方形的长为3×2=6(厘米)。长方形的周长为3+6=9(厘米),9×2=18(厘米),面积为:3×6=18(平方厘米)。
10.A
11.A
12.B
13.×
14.×
15.×
16.×
17.√
18.根据第一个图可知,阴影部分面积=半圆的面积-三角形的面积,根据半圆的面积公式:S=πr2÷2,三角形的面积公式:底×高÷2,把数代入即可求解。
根据第二个图可知,阴影部分面积=正方形的面积-圆的面积,根据圆的面积公式:πr2×,正方形的面积公式:边长×边长,把数代入即可求解。
三角形面积:12×4÷2
=48÷2
=24(cm2)
半圆面积:3.14×(12÷2)2÷2
=3.14×36÷2
=113.04÷2
=56.52(cm2)
阴影部分面积:56.52-24=32.52(cm2);
正方形面积:8×8=64(cm2)
圆的面积: 3.14×8×8×
=25.12×8×
=50.24(cm2)
阴影部分面积:64-50.24=13.76(cm2)
19.3.14×6×6=113.04(平方厘米)
18.84÷113.04×360=60(度)
答:它的圆心角是60度.
20.圆心角是100度,用100除以360求出圆心角占360度的几分之几,那么扇形面积就占所在圆面积的几分之几.
12÷2=6(厘米)
3.14×6×6=113.04(平方厘米)
113.04×=31.4(平方厘米)
答:这个扇形的面积是31.4平方厘米.
21.试题分析:由题意可知:这只羊能吃到的草的部分是一个以正方形的边长为半径的圆,其周长已知,于是可以求出其半径,进而依据“吃不到的面积=正方形的面积﹣吃到草的面积”,据此代入数据即可求解.
解:设正方形的边长为a,
则2a+×2×3.14×a=6.28,
2a+1.57a=6.28,
3.57a=6.28,
a=,
﹣,
=0.215×,
≈0.7(平方米);
答:这只羊吃不到草部分的面积约是0.7平方米。
22.设OA=2r
因为,∠BOA=90°,所以,S扇形AOB=,
又因为∠AOD=45°,所以S扇形AOD=S扇形AOB=πr2,
S半圆=πr2,
所以:S阴影=图中①的面积=1平方厘米
23.3.14×3×2÷360°×120°×3
=9.42×2÷360°×120°×3
=18.84÷360°×120°×3
=18.84(厘米)
答:B点从开始到结束经过的路线的总长度是18.84厘米.
24.根据题干三角形ABC是等边三角形,所以每个角的度数都是60°,那么图中就出现了3个半径为6厘米,圆心角为60°的扇形;这三段弧所围成的图形的面积=三个扇形的面积之和﹣2个等边三角形的面积,由此利用扇形的面积公式和三角形的面积公式即可解决问题.
解:一个小扇形的面积是:×3.14×62,
=×3.14×36,
=18.84(平方厘米),
等边三角形的面积为:6×5.2÷2=15.6(平方厘米),
所以这三段弧所围成的图形的面积是:18.84×3﹣15.6×2=56.52﹣31.2=25.32(平方厘米),
答:这三段弧所围成的图形的面积是25.32平方厘米。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 比和百分比
- 1、生活中的比
- 2、比与除法
- 3、比的基本性质
- 4、图形的放大和缩小
- 5、比的应用
- 6、认识百分比
- 7、小数或分数化成百分比
- 8、百分数化成小数或分数
- 9、百分数的应用(一)
- 10、百分数的应用(二)
- 二 分数和百分数应用问题
- 11、应用问题(一)
- 12、应用问题(二)
- 13、折扣和利润
- 14、利息和纳税
- 三 圆的周长与面积
- 15、圆的周长
- 16、圆的面积
- 17、圆与正方形
- 18、扇形
- 四 统计与可能性
- 19、扇形统计图
- 20、可能性大小
- 21、身高和体重
- 五 用水中的数学问题
- 22、地球水资源
- 23、中国水资源
- 24、分析用水量
- 25、节约用水
- 26、防止水污染
- 六 总复习
- 总复习
