2024届人教版八年级数学上册第12章 全等三角形复习与小结 同步课件(共26张PPT)
文档属性
| 名称 | 2024届人教版八年级数学上册第12章 全等三角形复习与小结 同步课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 687.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 08:56:07 | ||
图片预览




文档简介
(共26张PPT)
第12章全等三角形复习与小结
人教版数学八年级上册
全等三角形
1.全等三角形的定义
2.全等三角形的表示方法和有关概念
3.全等三角形的性质及实际应用
三角形全等的判定
1.三边对应相等(SSS)
2.两边及其夹角对应相等(SAS)
3.两角及其夹边对应相等(ASA)
4.两角及其中一角的对边对应相等(AAS)
5.斜边和一条直角边对应相等(HL)
角的平分线
1.性质:角的平分线上的点到角的两边的距离相等
2.判定:角的内部到角的两边的距离相等的点在角的平分线上
知识梳理
知识点一 全等三角形
1.全等三角形的定义
能够完全重合的两个三角形叫做全等三角形.
重合的点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
2.全等三角形的表示方法
全等用符号“≌”表示,记作“△ABC≌△DEF”.
A
B
C
D
E
F
知识梳理
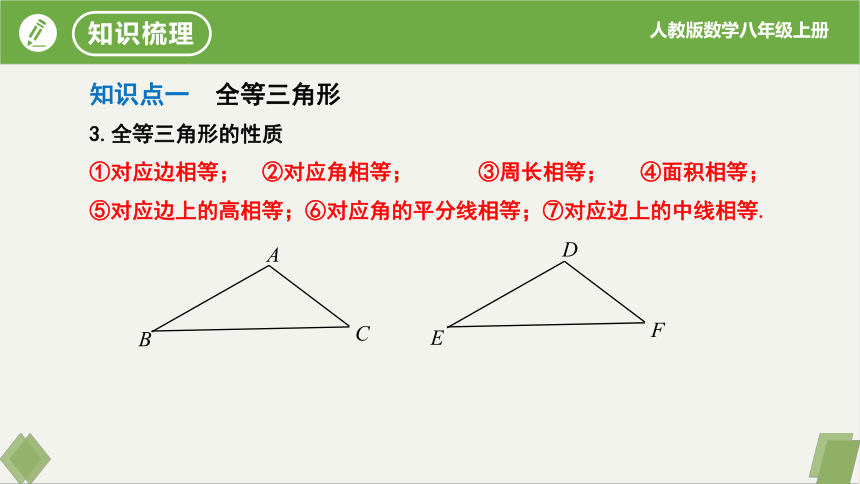
3.全等三角形的性质
知识点一 全等三角形
①对应边相等; ②对应角相等; ③周长相等; ④面积相等;
⑤对应边上的高相等;⑥对应角的平分线相等;⑦对应边上的中线相等.
A
B
C
D
E
F
知识梳理
∵△ABC≌△BAD且点A和点B,点C和点D是对应顶点,
∴ AB=BA,AC=BD,BC=AD.
∵AD=9cm,
∴BC=9cm.
1.△ABC≌△BAD,若点A和点B,点C和点D是对应顶点,如果AB=4cm,BD=6cm,AD=9cm,,那么BC的长是( )
A.4cm B.6cm C.9cm D.不能确定
C
课堂检测
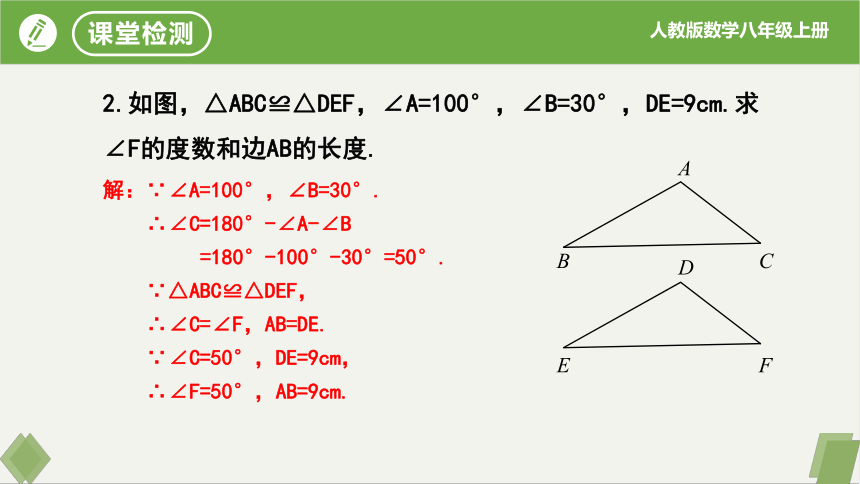
解:∵∠A=100°,∠B=30°.
∴∠C=180°-∠A-∠B
=180°-100°-30°=50°.
∵△ABC≌△DEF,
∴∠C=∠F,AB=DE.
∵∠C=50°,DE=9cm,
∴∠F=50°,AB=9cm.
A
D
F
E
B
C
2.如图,△ABC≌△DEF,∠A=100°,∠B=30°,DE=9cm.求∠F的度数和边AB的长度.
课堂检测
课堂检测
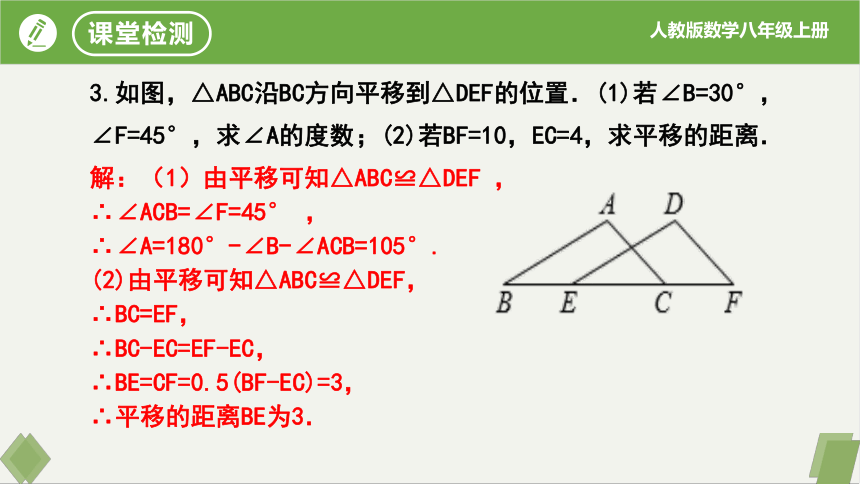
3.如图,△ABC沿BC方向平移到△DEF的位置.(1)若∠B=30°,∠F=45°,求∠A的度数;(2)若BF=10,EC=4,求平移的距离.
解:(1)由平移可知△ABC≌△DEF ,
∴∠ACB=∠F=45° ,
∴∠A=180°-∠B-∠ACB=105°.
(2)由平移可知△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF=0.5(BF-EC)=3,
∴平移的距离BE为3.
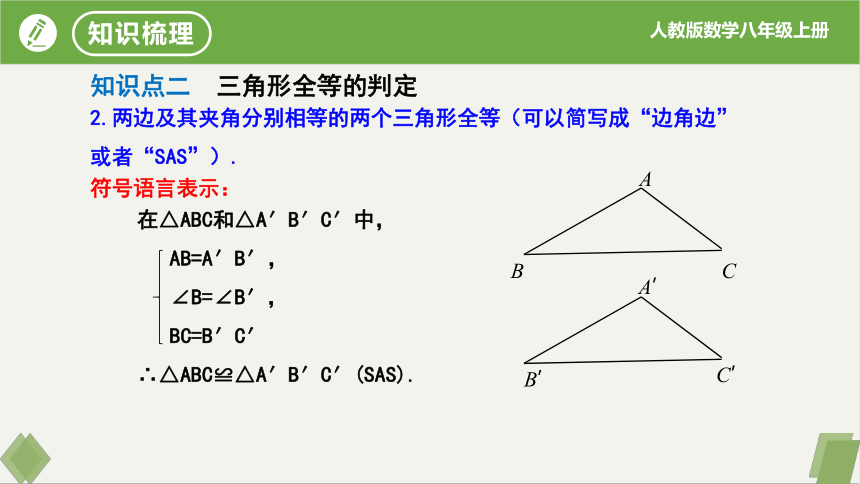
知识点二 三角形全等的判定
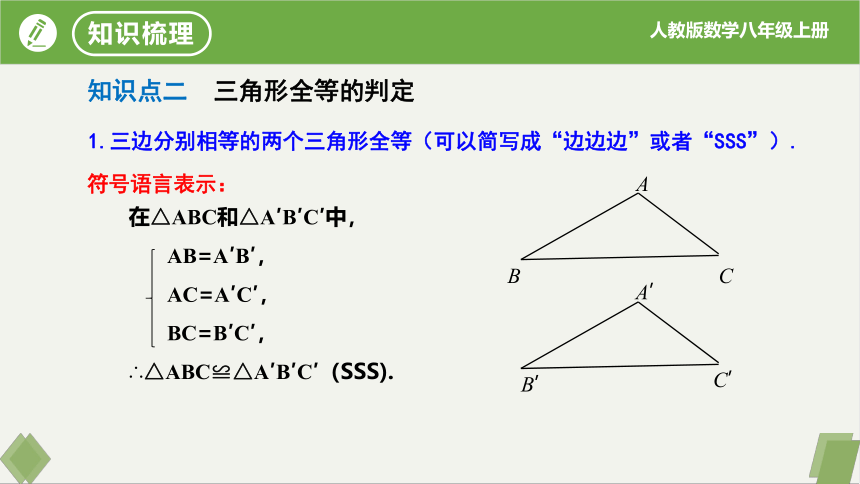
在△ABC和△A′B′C′中,
AB=A′B′,
AC=A′C′,
BC=B′C′,
∴△ABC≌△A′B′C′(SSS).
1.三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
A
B
C
A’
B’
C’
符号语言表示:
知识梳理
知识点二 三角形全等的判定
A
B
C
A’
B’
C’
符号语言表示:
在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′
∴△ABC≌△A′B′C′(SAS).
2.两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或者“SAS”).
知识梳理
知识点二 三角形全等的判定
A
B
C
A’
B’
C’
符号语言表示:
3.两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
在△ABC和△A′B′C′中,
∠B=∠B′,
BC=∠B′C′,
∠C=∠C′, ∴△ABC≌△A′B′C′(ASA).
知识梳理
知识点二 三角形全等的判定
A
B
C
A’
B’
C’
符号语言表示:
4.两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或者“AAS”).
在△ABC和△A′B′C′中,
∠A=∠A′,
∠B=∠B′,
BC=B′C′, ∴△ABC≌△A′B′C′(AAS).
知识梳理
知识点二 三角形全等的判定
符号语言表示:
A
B
C
B′
A′
┐
┐
C′
在Rt△ABC和Rt△A′B′C′中,
AC=A′C′,
BC=B′C′, ∴△ABC≌△A′B′C′(HL).
5.斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或者“HL”) .
知识梳理
证明两个三角形全等的基本类型
已知两边
找第三边“SSS”
找两边的夹角“SAS”
看是否是直角三角形,若是“HL”
已知两角
找两角的夹边“ASA”
找任意一角的对边“AAS”
已知一边
一角
一边和它的邻角
一边和它的对角
找这个角的另外一边“SAS”
找这条边的对角“AAS”
看这个角是否是直角,若是,找任意一条直角边“HL”
找另外任意一个角“AAS”
找这条边的另外一个邻角“ASA”
知识梳理
1.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
证明:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE ,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS)
∴∠C=∠E.
课堂检测
课堂检测
(2)∵△ABC≌△ADE
∴∠B=∠D
在△ABM和△ADN中,
∴△ABM≌△AND(ASA)
∴AM=AN.
1.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
证明:方法一:在线段AB上截取AF=AC,连接EF.
∵AE,BE分别平分∠CAB和∠DBA,
∴∠1=∠2,∠3=∠4.
在△ACE和△AFE中,
AC=AF,
∠1=∠2,
AE=AE,
∴△ACE≌△AFE(SAS).
∴∠5=∠C.
课堂检测
∵AC//BD,
∴∠C+∠D=180°.
∵∠5+∠6=180°,
∴∠6=∠D.
在△EFB和△EDB中,
∠6=∠D,
∠3=∠4,
BE=BE,
∴△EFB≌△EDB(AAS).
∴FB=BD.
∴AB=AF+FB=AC+BD,即AB=AC+BD.
(截长法)
课堂检测
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
证明:方法二:延长AC至点F,使得AF=AB,连接EF
∵AE,BE分别平分∠CAB和∠DBA.
∴∠1=∠2,∠3=∠4.
∵在△AEF和△AEB中, AF=AB,
∠1=∠2,
AE=AE,
∴△ACE≌△AFE(SAS) ∴EF=EB,∠F=∠3.
课堂检测
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
∵∠3=∠4, ∴∠F=∠4.
∵AC//BD, ∴∠FCE=∠D.
∵在△CEF和△DEB中, ∠FCE=∠D,
∠F=∠4,
EF=EB,
∴△CEF≌△DEB(AAS) ∴CF=BD.
∵AB=AF=AC+CF, ∴AB=AC+BD.
(补短法)
课堂检测
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
(1)截长法,即在长线段上截取一段,使其等于其中一短线段,然后证明剩下的线段等于另一短线段;
(2)补短法,即延长短线段,使其延长部分等于另一短线段,再证明延长后的线段等于长线段,或者延长短线段,使其等于长线段,然后证明延长的部分等于另一短线段.
“倍长中线法”构造全等三角形解决问题:
总结归纳
知识点三 角的平分线
1.作已知角的平分线
作法:(1)以点O为圆心,适当长为半径画弧线,交OA于点N,交OB于点M.
(2)分别以M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC,射线OC即为所求.
知识梳理
2.角的平分线的性质:角的平分线上的点到角的两边的距离相等.
知识点三 角的平分线
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE.
符号语言表示:
3.角的平分线的判定:角的内部到角的两边距离相等的点在角的平分线上.
符号语言表示:
∵PD⊥OA,PE⊥OB,且PD=PE.
∴点P在∠AOB的平分线OC上.
知识梳理
课堂检测
1.如图,在四边形ABCD中,BC=DC,CE⊥AB于E.若∠B+∠ADC=180°,求证:AC平分∠BAD.
证明:如图,过点C作CF⊥AD,交AD的延长线于F,
∵∠B+∠ADC=180°,∠ADC+∠CDF=180°,
∴∠B=∠CDF.
在△CBE和△CDF中,
∠B=∠CDF, ∠CEB=∠CFD=90°,BC=CD,
∴△CBE≌△CDF(AAS).
∴CF=CE.
∵CF⊥AD,CE⊥AB,
∴AC平分∠BAD.
F
2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
证明:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB.
∴∠POD=∠POE,DP=EP.
∴∠DPF=∠POD+∠ODP,∠EPF=∠POE+∠OEP.
∴∠DPF=∠EPF.
在△DPF和△EPF中, DP=EP,
∠DPF=∠EPF,
PF=PF,
∴△DPF≌△EPF(SAS). ∴DF=EF.
O
B
A
C
P
E
D
┐
┐
F
课堂检测
3.如图,∠AOB=90°,OM平分∠AOB,直角三角板的直角顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D.请判断PC与PD的数量关系并说明理由.
解:PC=PD.理由如下:
如图,过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°.
∵∠EOF=90°,∴∠FPE=90°.
∵OM是∠AOB的平分线,∴PE=PF.
由题意知∠CPD=90°,
∴∠1+∠FPD=90°.
∵∠2+∠FPD=90°,
∴∠1=∠2.
在△CFP和△DEP中,∠CFP=∠DEP,PF=PE, ∠1=∠2
∴△CFP≌△DEP(ASA).
∴PC=PD.
课堂检测
谢谢聆听
第12章全等三角形复习与小结
人教版数学八年级上册
全等三角形
1.全等三角形的定义
2.全等三角形的表示方法和有关概念
3.全等三角形的性质及实际应用
三角形全等的判定
1.三边对应相等(SSS)
2.两边及其夹角对应相等(SAS)
3.两角及其夹边对应相等(ASA)
4.两角及其中一角的对边对应相等(AAS)
5.斜边和一条直角边对应相等(HL)
角的平分线
1.性质:角的平分线上的点到角的两边的距离相等
2.判定:角的内部到角的两边的距离相等的点在角的平分线上
知识梳理
知识点一 全等三角形
1.全等三角形的定义
能够完全重合的两个三角形叫做全等三角形.
重合的点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
2.全等三角形的表示方法
全等用符号“≌”表示,记作“△ABC≌△DEF”.
A
B
C
D
E
F
知识梳理
3.全等三角形的性质
知识点一 全等三角形
①对应边相等; ②对应角相等; ③周长相等; ④面积相等;
⑤对应边上的高相等;⑥对应角的平分线相等;⑦对应边上的中线相等.
A
B
C
D
E
F
知识梳理
∵△ABC≌△BAD且点A和点B,点C和点D是对应顶点,
∴ AB=BA,AC=BD,BC=AD.
∵AD=9cm,
∴BC=9cm.
1.△ABC≌△BAD,若点A和点B,点C和点D是对应顶点,如果AB=4cm,BD=6cm,AD=9cm,,那么BC的长是( )
A.4cm B.6cm C.9cm D.不能确定
C
课堂检测
解:∵∠A=100°,∠B=30°.
∴∠C=180°-∠A-∠B
=180°-100°-30°=50°.
∵△ABC≌△DEF,
∴∠C=∠F,AB=DE.
∵∠C=50°,DE=9cm,
∴∠F=50°,AB=9cm.
A
D
F
E
B
C
2.如图,△ABC≌△DEF,∠A=100°,∠B=30°,DE=9cm.求∠F的度数和边AB的长度.
课堂检测
课堂检测
3.如图,△ABC沿BC方向平移到△DEF的位置.(1)若∠B=30°,∠F=45°,求∠A的度数;(2)若BF=10,EC=4,求平移的距离.
解:(1)由平移可知△ABC≌△DEF ,
∴∠ACB=∠F=45° ,
∴∠A=180°-∠B-∠ACB=105°.
(2)由平移可知△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF=0.5(BF-EC)=3,
∴平移的距离BE为3.
知识点二 三角形全等的判定
在△ABC和△A′B′C′中,
AB=A′B′,
AC=A′C′,
BC=B′C′,
∴△ABC≌△A′B′C′(SSS).
1.三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
A
B
C
A’
B’
C’
符号语言表示:
知识梳理
知识点二 三角形全等的判定
A
B
C
A’
B’
C’
符号语言表示:
在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′
∴△ABC≌△A′B′C′(SAS).
2.两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或者“SAS”).
知识梳理
知识点二 三角形全等的判定
A
B
C
A’
B’
C’
符号语言表示:
3.两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
在△ABC和△A′B′C′中,
∠B=∠B′,
BC=∠B′C′,
∠C=∠C′, ∴△ABC≌△A′B′C′(ASA).
知识梳理
知识点二 三角形全等的判定
A
B
C
A’
B’
C’
符号语言表示:
4.两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或者“AAS”).
在△ABC和△A′B′C′中,
∠A=∠A′,
∠B=∠B′,
BC=B′C′, ∴△ABC≌△A′B′C′(AAS).
知识梳理
知识点二 三角形全等的判定
符号语言表示:
A
B
C
B′
A′
┐
┐
C′
在Rt△ABC和Rt△A′B′C′中,
AC=A′C′,
BC=B′C′, ∴△ABC≌△A′B′C′(HL).
5.斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或者“HL”) .
知识梳理
证明两个三角形全等的基本类型
已知两边
找第三边“SSS”
找两边的夹角“SAS”
看是否是直角三角形,若是“HL”
已知两角
找两角的夹边“ASA”
找任意一角的对边“AAS”
已知一边
一角
一边和它的邻角
一边和它的对角
找这个角的另外一边“SAS”
找这条边的对角“AAS”
看这个角是否是直角,若是,找任意一条直角边“HL”
找另外任意一个角“AAS”
找这条边的另外一个邻角“ASA”
知识梳理
1.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
证明:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE ,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS)
∴∠C=∠E.
课堂检测
课堂检测
(2)∵△ABC≌△ADE
∴∠B=∠D
在△ABM和△ADN中,
∴△ABM≌△AND(ASA)
∴AM=AN.
1.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
证明:方法一:在线段AB上截取AF=AC,连接EF.
∵AE,BE分别平分∠CAB和∠DBA,
∴∠1=∠2,∠3=∠4.
在△ACE和△AFE中,
AC=AF,
∠1=∠2,
AE=AE,
∴△ACE≌△AFE(SAS).
∴∠5=∠C.
课堂检测
∵AC//BD,
∴∠C+∠D=180°.
∵∠5+∠6=180°,
∴∠6=∠D.
在△EFB和△EDB中,
∠6=∠D,
∠3=∠4,
BE=BE,
∴△EFB≌△EDB(AAS).
∴FB=BD.
∴AB=AF+FB=AC+BD,即AB=AC+BD.
(截长法)
课堂检测
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
证明:方法二:延长AC至点F,使得AF=AB,连接EF
∵AE,BE分别平分∠CAB和∠DBA.
∴∠1=∠2,∠3=∠4.
∵在△AEF和△AEB中, AF=AB,
∠1=∠2,
AE=AE,
∴△ACE≌△AFE(SAS) ∴EF=EB,∠F=∠3.
课堂检测
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
∵∠3=∠4, ∴∠F=∠4.
∵AC//BD, ∴∠FCE=∠D.
∵在△CEF和△DEB中, ∠FCE=∠D,
∠F=∠4,
EF=EB,
∴△CEF≌△DEB(AAS) ∴CF=BD.
∵AB=AF=AC+CF, ∴AB=AC+BD.
(补短法)
课堂检测
2.如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.
(1)截长法,即在长线段上截取一段,使其等于其中一短线段,然后证明剩下的线段等于另一短线段;
(2)补短法,即延长短线段,使其延长部分等于另一短线段,再证明延长后的线段等于长线段,或者延长短线段,使其等于长线段,然后证明延长的部分等于另一短线段.
“倍长中线法”构造全等三角形解决问题:
总结归纳
知识点三 角的平分线
1.作已知角的平分线
作法:(1)以点O为圆心,适当长为半径画弧线,交OA于点N,交OB于点M.
(2)分别以M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC,射线OC即为所求.
知识梳理
2.角的平分线的性质:角的平分线上的点到角的两边的距离相等.
知识点三 角的平分线
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE.
符号语言表示:
3.角的平分线的判定:角的内部到角的两边距离相等的点在角的平分线上.
符号语言表示:
∵PD⊥OA,PE⊥OB,且PD=PE.
∴点P在∠AOB的平分线OC上.
知识梳理
课堂检测
1.如图,在四边形ABCD中,BC=DC,CE⊥AB于E.若∠B+∠ADC=180°,求证:AC平分∠BAD.
证明:如图,过点C作CF⊥AD,交AD的延长线于F,
∵∠B+∠ADC=180°,∠ADC+∠CDF=180°,
∴∠B=∠CDF.
在△CBE和△CDF中,
∠B=∠CDF, ∠CEB=∠CFD=90°,BC=CD,
∴△CBE≌△CDF(AAS).
∴CF=CE.
∵CF⊥AD,CE⊥AB,
∴AC平分∠BAD.
F
2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
证明:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB.
∴∠POD=∠POE,DP=EP.
∴∠DPF=∠POD+∠ODP,∠EPF=∠POE+∠OEP.
∴∠DPF=∠EPF.
在△DPF和△EPF中, DP=EP,
∠DPF=∠EPF,
PF=PF,
∴△DPF≌△EPF(SAS). ∴DF=EF.
O
B
A
C
P
E
D
┐
┐
F
课堂检测
3.如图,∠AOB=90°,OM平分∠AOB,直角三角板的直角顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D.请判断PC与PD的数量关系并说明理由.
解:PC=PD.理由如下:
如图,过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°.
∵∠EOF=90°,∴∠FPE=90°.
∵OM是∠AOB的平分线,∴PE=PF.
由题意知∠CPD=90°,
∴∠1+∠FPD=90°.
∵∠2+∠FPD=90°,
∴∠1=∠2.
在△CFP和△DEP中,∠CFP=∠DEP,PF=PE, ∠1=∠2
∴△CFP≌△DEP(ASA).
∴PC=PD.
课堂检测
谢谢聆听
