8.2.2函数的实际应用讲义——2023-2024学年高一上学期数学苏教版(2019)必修第一册
文档属性
| 名称 | 8.2.2函数的实际应用讲义——2023-2024学年高一上学期数学苏教版(2019)必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 848.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 16:18:14 | ||
图片预览



文档简介
编号:055 课题: 8.2.2 函数的实际应用
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握解答函数应用题的操作步骤;
2.掌握应用问题中的变量关系;
3.会利用函数模型解决实际问题;
4.理解并掌握实际问题中函数模型的选择问题(数学建模).
本节重点难点
重点:利用函数模型解决实际问题;
难点:实际问题中函数模型的选择问题(数学建模).
学科素养目标
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
教学过程赏析
基础知识积累
解决函数应用问题的一般程序是:
审题,设未知量;
寻找等量关系;
列出方程;
解方程;
验根或证明;
结论或作答.
【课前基础演练】
题1. 某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系 (e=2.718…为自然对数的底数,k,b为常数),若该食品在0 ℃时的保鲜时间是192小时,在22 ℃时的保鲜时间是48小时,则该食品在33 ℃时的保鲜时间是____小时 ( )
A.22 B.23 C.24 D.33
题2.据报道,全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度,设2018年北冰洋冬季冰雪覆盖面积为m,则从2018年起,x年后北冰洋冬季冰雪覆盖面积y与x的函数关系式是( )
A.y=
B.y=
C.y=0.9550-x·m
D.y=(1-0.0550-x)·m
题3.某特种冰箱的食物保鲜时间y(单位:小时)与设置储存温度x(单位:℃)近似满足函数关系y=3kx+b(k,b为常数),若设置储存温度0 ℃的保鲜时间是288小时,设置储存温度5 ℃的保鲜时间是144小时,则设置储存温度15 ℃的保鲜时间近似是( )
A.36小时 B.48小时
C.60小时 D.72小时
题4.光线通过一块玻璃,强度要损失10%.设光线原来的强度为k,通过x块这样的玻璃以后强度为y,则经过x块这样的玻璃后光线强度为,那么至少通过____块这样的玻璃,光线强度能减弱到原来的以下() ( )
A.12 B.13 C.14 D.15
题5.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是( )
A.y=0.2x B.y=0.1(x2+2x) C.y= D.y=0.2+log16x
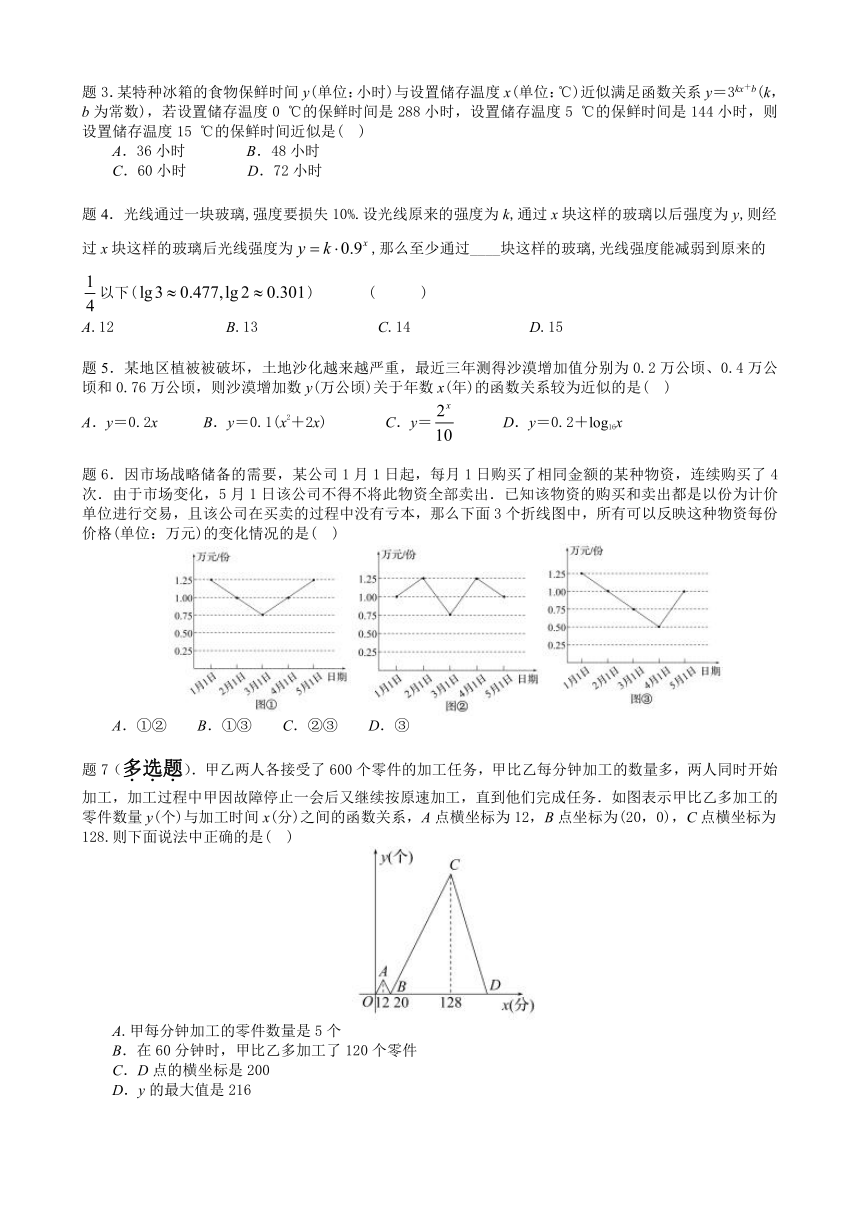
题6.因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面3个折线图中,所有可以反映这种物资每份价格(单位:万元)的变化情况的是( )
A.①② B.①③ C.②③ D.③
题7(多选题).甲乙两人各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为12,B点坐标为(20,0),C点横坐标为128.则下面说法中正确的是( )
A.甲每分钟加工的零件数量是5个
B.在60分钟时,甲比乙多加工了120个零件
C.D点的横坐标是200
D.y的最大值是216
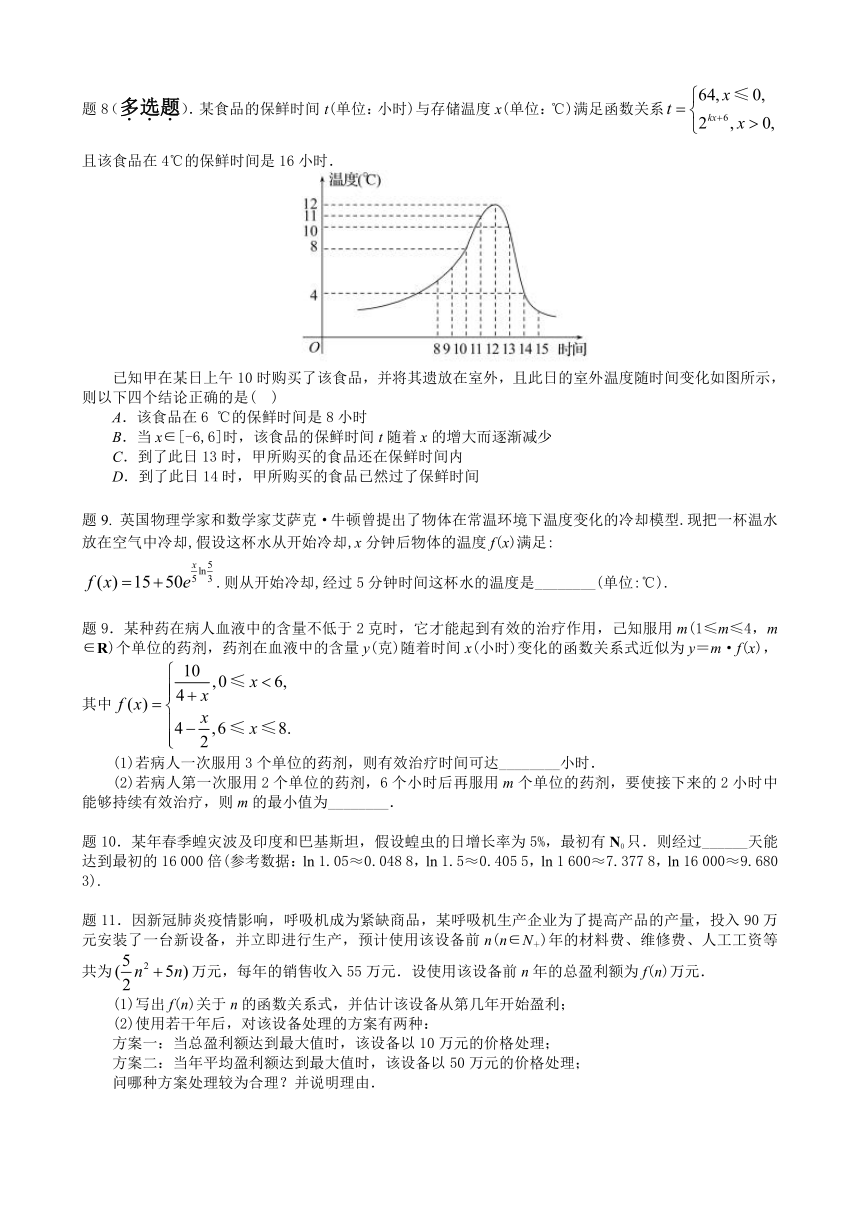
题8(多选题).某食品的保鲜时间t(单位:小时)与存储温度x(单位:℃)满足函数关系且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,则以下四个结论正确的是( )
A.该食品在6 ℃的保鲜时间是8小时
B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少
C.到了此日13时,甲所购买的食品还在保鲜时间内
D.到了此日14时,甲所购买的食品已然过了保鲜时间
题9. 英国物理学家和数学家艾萨克·牛顿曾提出了物体在常温环境下温度变化的冷却模型.现把一杯温水放在空气中冷却,假设这杯水从开始冷却,x分钟后物体的温度f(x)满足:
.则从开始冷却,经过5分钟时间这杯水的温度是________(单位:℃).
题9.某种药在病人血液中的含量不低于2克时,它才能起到有效的治疗作用,己知服用m(1≤m≤4,m∈R)个单位的药剂,药剂在血液中的含量y(克)随着时间x(小时)变化的函数关系式近似为y=m·f(x),其中
(1)若病人一次服用3个单位的药剂,则有效治疗时间可达________小时.
(2)若病人第一次服用2个单位的药剂,6个小时后再服用m个单位的药剂,要使接下来的2小时中能够持续有效治疗,则m的最小值为________.
题10.某年春季蝗灾波及印度和巴基斯坦,假设蝗虫的日增长率为5%,最初有N0只.则经过______天能达到最初的16 000倍(参考数据:ln 1.05≈0.048 8,ln 1.5≈0.405 5,ln 1 600≈7.377 8,ln 16 000≈9.680 3).
题11.因新冠肺炎疫情影响,呼吸机成为紧缺商品,某呼吸机生产企业为了提高产品的产量,投入90万元安装了一台新设备,并立即进行生产,预计使用该设备前n(n∈N+)年的材料费、维修费、人工工资等共为万元,每年的销售收入55万元.设使用该设备前n年的总盈利额为f(n)万元.
(1)写出f(n)关于n的函数关系式,并估计该设备从第几年开始盈利;
(2)使用若干年后,对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以10万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以50万元的价格处理;
问哪种方案处理较为合理?并说明理由.
【课堂检测达标】
题12.某种电热水器的水箱盛满水是200升,加热到一定温度可浴用.浴用时,已知每分钟放水34升,在放水的同时注水,t分钟注水2t2升,当水箱内水量达到最小值时,放水自动停止.现假定每人洗浴用水65升,则该热水器一次至多可供几人洗澡( )
A.3人 B.4人 C.5人 D.6人
题13.心理学家有时使用函数L(t)=A(1-e-kt)来测定一个人在时间t(min)内能够记忆的量L,其中A表示需要记忆的量,k表示记忆率.假设一个学生有200个单词要记忆,心理学家测定在5 min内该学生能够记忆20个单词.则记忆率k所在区间为( )
A. B.
C. D.
题14(多选题).一家货物公司计划租地建造仓库储存货物,经市场调查了解到下列信息:每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费y2(单位:万元)与x成正比,若在距离车站10 km处建仓库,则y1为1万元,y2为4万元,下列结论正确的是( )
A.y1=x (1) B.y2=0.4x C.y1+y2有最小值4 D.y1-y2无最小值
题15(多选题).据某国学者詹姆斯·马丁的测算,近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度.因此,基础教育的任务已不是教会一切人一切知识,而是让一切人学会学习.已知2002年底,人类知识总量为a,假如从2002年底到2012年底是每三年翻一番,从2012年底到2022年底是每一年翻一番,2023年(按365天计算)是每73天翻一番,则下列说法正确的是
A.2008年底人类知识总量是2a B.2012年底人类知识总量是8a ( )
C.2022年底人类知识总量是213a D.2023年底人类知识总量是218a
题16.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份0.8元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸________份.
题17.某制造商制造并出售圆柱形瓶装的某种饮料,瓶子的底面半径是r,高h=r(单位:cm),一个瓶子的制造成本是0.8πr2分,已知每出售1 mL(注:1 mL=1 cm3)的饮料,制造商可获利0.2分,且制造商能制造的瓶子底面的最大半径为6 cm.记每瓶饮料的利润为f(r),则f(3)=________,其实际意义是____________.
题18.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=-48x+8 000,已知此生产线年产量最大为230吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本P(年总成本除以年产量)最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,且生产的产品全部售完,那么当年产量为多少吨时,年总利润可以获得最大?最大利润是多少?
题19.销售甲、乙两种商品所得利润分别是y1,y2万元,它们与投入资金x万元的关系分别为y1=m+a,y2=bx(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示.
(1)求函数y1与y2的解析式;
(2)若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值.
【综合突破拔高】
题20. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如表所示的关系.
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p元,则x,p分别为( )
A.35,225 B.40,300 C.45,350 D.45,400
题21.某商场对顾客实行购物优惠活动,规定一次购物:
(1)如不超过200元,则不予优惠;
(2)如超过200元但不超过500元,则全款按9折优惠;
(3)如超过500元,其中500元按9折给予优惠,超过500的部分按8折给予优惠.
某人两次去购物,分别付款168元和423元,若他只去一次购买同样价格的商品,则应付款( )
A.472.8元 B.510.4元 C.522.8元 D.560.4元
题22.已知样本中碳14的质量N随时间t(年)的衰变规律满足:N=N0·(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log2 3≈1.6,log2 5≈2.3)
A.3440年 B.4010年
C.4580年 D.5160年
题23. 8月到11月这四个月的某产品价格的市场平均价f(x)(单位:元/千克)与时间x(单位:月份)的数据如表
x 8 9 10 11
f(x) 28.00 33.99 36.00 34.02
现有三种函数模型:①f(x)=bx+a;②f(x)=ax2+bx+c;③f(x)=+a,找出你认为最适合的函数模型,并估计2020年12月份的该产品市场平均价( )
A.②,28元/千克
B.①,25元/千克
C.②,23元/千克
D.③,21元/千克
题24.声强级L1(单位:dB)与声强I的函数关系式为:L1=10lg.若普通列车的声强级是95 dB,高速列车的声强级为45 dB,则普通列车的声强是高速列车声强的( )
A.106倍 B.105倍 C.104倍 D.103倍
题25(多选题). “双11”购物节中,某电商对顾客实行购物优惠活动,规定一次购物付款总额满一定额度,可以给予优惠:
(1)如果购物总额不超过50元,则不给予优惠;
(2)如果购物总额超过50元但不超过100元,可以使用一张5元优惠券;
(3)如果购物总额超过100元但不超过300元,则按标价给予9折优惠;
(4)如果购物总额超过300元,其中300元内的按第(3)条给予优惠,超过300元的部分给予8折优惠.
某人购买了部分商品,则下列说法正确的是 ( )
A.如果购物总额为78元,则应付款为73元 B.如果购物总额为228元,则应付款为205.2元
C.如果购物总额为368元,则应付款为294.4元
D.如果购物时一次性全部付款442.8元,则购物总额为516元
题26(多选题).某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用y1(千元),乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示,则下列说法正确的是 ( )
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的总费用y1与证书数量x之间的函数关系式为y1=0.5x+1
C.若该单位需印制证书数量为8千个,则该单位选择甲厂更节省费用
D.当印制证书数量超过2千个时,乙厂的总费用y2与证书数量x之间的函数关系式为y2=x+
题27.某项研究表明:在考虑行车安全的情况下,某路段车流量F(单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v(假设车辆以相同速度v行驶,单位:米/秒)、平均车长l(单位:米)的值有关,其公式为F=.
(1)如果不限定车型,l=6.05,则最大车流量为________辆/小时;
(2)如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加______辆/小时.
题28.某种细菌经30分钟数量变为原来的2倍,且该种细菌的繁殖规律为y=ekt,其中k为常数,t表示时间(单位:小时),y表示繁殖后细菌总个数,经过5小时,1个细菌通过繁殖个数变为________.
题29.已知14C的半衰期为5 730年(是指经过5 730年后,14C的残余量占原始量的一半).设14C的原始量为a,经过x年后的残余量为b,残余量b与原始量a的关系如下:b=ae-kx,其中x表示经过的时间,k为一个常数.现测得湖南长沙马王堆汉墓女尸出土时14C的残余量约占原始量的76.7%.请你推断一下马王堆汉墓的大致年代为距今________年.(已知log20.767≈-0.4,ln 2≈0.69)
题30.为节约能源,倡导绿色环保,某主题公园有60辆电动观光车供租赁使用,管理这些电动观光车的费用是每日120元.根据经验,若每辆电动观光车的日租金不超过5元,则电动观光车可以全部租出;若超过5元,则每超过1元,租不出去的电动观光车就增加2辆.为了便于结算,每辆电动观光车的日租金x(元)只取整数,并且要求出租电动观光车一日的收入必须高于这一日的管理费用,用y(元)表示出租电动观光车的日净收入(即一日出租电动观光车的总收入减去管理费用后的所得).
(1)求y关于x的解析式及其定义域;(2)当每辆电动观光车的日租金为多少元时,才能使一日的净收入最多?
题31. 小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为W(x)万元.在年产量不足万件时,(万元);在年产量不小于8万件时, (万元).每件产品售价为5元.通过市场分析,小王生产的商 品当年能全部售完.写出年利润L(x)(万元)关于年产量x(万件)的函数解析式.(注:年利润=年销售收入-固定成本-流动成本)
题32.围建一个面积为360的矩形场地,要求矩形场地的一面利用30 m的旧墙(利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m).
分别写出矩形场地的另一边长C(单位:m)、旧墙维修费用P(单位:元)、新墙的造价R(单位:元)、建设矩形场地的总费用L(单位:元)关于利用旧墙的长度x(单位:m)的函数关系式.
题33.运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择,它们的速度分别为60千米/小时、120千米/小时,500千米/小时,每千米的运费分别为:20元、10元、50元.这批海鲜在运输过程中每小时的损耗为m元(m>0),运输的路程为s(千米).设用汽车、火车、飞机三种运输工具运输时各自的总费用(包括运费和损耗费)分别为y1(元),y2(元),y3(元).
(1)请分别写出y1,y2,y3的表达式;
(2)试确定使用哪种运输工具总费用最省.
题34.据调查:人类在能源利用与森林砍伐中使CO2浓度增加.据测,2015年,2016年,2017年大气中的CO2浓度分别比2014年增加了1个单位,3个单位,6个单位.若用一个函数模拟每年CO2浓度增加的单位数y与年份增加数x的关系,模拟函数可选用二次函数f(x)=px2+qx+r(其中p,q,r为常数)或函数g(x)=a·bx+c(其中a,b,c为常数),又知2018年大气中的CO2浓度比2014年增加了16.5个单位,请问用以上哪个函数作模拟函数较好
编号:055 课题: 8.2.2 函数的实际应用
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握解答函数应用题的操作步骤;
2.掌握应用问题中的变量关系;
3.会利用函数模型解决实际问题;
4.理解并掌握实际问题中函数模型的选择问题(数学建模).
本节重点难点
重点:利用函数模型解决实际问题;
难点:实际问题中函数模型的选择问题(数学建模).
学科素养目标
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
教学过程赏析
基础知识积累
解决函数应用问题的一般程序是:
审题,设未知量;
寻找等量关系;
列出方程;
解方程;
验根或证明;
结论或作答.
【课前基础演练】
题1. 某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系 (e=2.718…为自然对数的底数,k,b为常数),若该食品在0 ℃时的保鲜时间是192小时,在22 ℃时的保鲜时间是48小时,则该食品在33 ℃时的保鲜时间是____小时 ( )
A.22 B.23 C.24 D.33
【思路导引】可通过整体代入法求解.
【解析】选C.某食品的保鲜时间y(单位:小时)与储存温度x(单位: ℃)满足函数关系 (e=2.718…为自然对数的底数,k,b为常数),该食品在0 ℃时的保鲜时间是192小时,在22 ℃时的保鲜时间是48小时,所以解得,
所以该食品在33 ℃时的保鲜时间:(小时).
题2.据报道,全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度,设2018年北冰洋冬季冰雪覆盖面积为m,则从2018年起,x年后北冰洋冬季冰雪覆盖面积y与x的函数关系式是( )
A.y=
B.y=
C.y=0.9550-x·m
D.y=(1-0.0550-x)·m
【解析】选A.设北冰洋每年冬季冰雪覆盖面积为上一年的q%.由题意可知(q%)50=0.95,所以q%=,所以从2018年起,x年后北冰洋冬季冰雪覆盖面积y与x的函数关系式为y=·m.
题3.某特种冰箱的食物保鲜时间y(单位:小时)与设置储存温度x(单位:℃)近似满足函数关系y=3kx+b(k,b为常数),若设置储存温度0 ℃的保鲜时间是288小时,设置储存温度5 ℃的保鲜时间是144小时,则设置储存温度15 ℃的保鲜时间近似是( )
A.36小时 B.48小时
C.60小时 D.72小时
【解析】选A.由题意可知
所以35k+b=35k×3b=144,所以35k=,
所以当x=15时,y=315k+b=315k×3b=(35k)3×3b=×288=×288=36,故设置储存温度15 ℃的保鲜时间近似是36小时.
题4.光线通过一块玻璃,强度要损失10%.设光线原来的强度为k,通过x块这样的玻璃以后强度为y,则经过x块这样的玻璃后光线强度为,那么至少通过____块这样的玻璃,光线强度能减弱到原来的以下() ( )
A.12 B.13 C.14 D.15
【解析】选C.光线经过x块玻璃后,强度变为.由题意,即,
两边同取对数,可得,因为,
所以,因为,所以.
即至少通过14块玻璃.
题5.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是( )
A.y=0.2x B.y=0.1(x2+2x) C.y= D.y=0.2+log16x
【解析】选C.因为三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,所以可以看出来不是线性增加,故选项A不符合题意;
对于选项B:把x=1,2,3分别代入解析式中得y=0.3,0.8,1.5,不符合题意;
对于选项C:把x=1,2,3分别代入解析式中得y=0.2,0.4,0.8,符合题意,
对于选项D:把x=1代入解析式中,得y=0.2,把x=2代入解析式中,得y=0.2+log162=0.45,把x=3代入解析式中,得y=0.2+log163=0.2+log23<0.2+log24=0.7,跟选项C来比,选项C更近似.
题6.因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面3个折线图中,所有可以反映这种物资每份价格(单位:万元)的变化情况的是( )
A.①② B.①③ C.②③ D.③
【解析】选B.设公司每月1日用于购买某种物资的金额为a万元.
题图①中四次购买的物资为,5月1日一次卖出物资得到,公司盈利,故①正确;
题图②中四次购买的物资为,5月1日一次卖出物资得到,公司亏损,故②错误;
题图③中四次购买的物资为,5月1日一次卖出物资得到,公司盈利,故③正确.
题7(多选题).甲乙两人各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为12,B点坐标为(20,0),C点横坐标为128.则下面说法中正确的是( )
A.甲每分钟加工的零件数量是5个
B.在60分钟时,甲比乙多加工了120个零件
C.D点的横坐标是200
D.y的最大值是216
【解析】选ACD.根据题意,甲一共加工的时间为(12-0)+(128-20)=120分钟,
一共加工了600个零件,则甲每分钟加工的数量是=5(个),所以选项A正确;
设D的坐标为(t,0),在区间(128,t)和(12,20)上,都是乙在加工,则直线AB和CD的斜率相等,则有∠ABO=∠CDB,在区间(20,128)和(0,12)上,甲乙同时加工,同理可得∠AOB=∠CBD,则△AOB∽△CBD,则有,解得t=200,即点D的坐标是(200,0),所以选项C正确;由题得乙每分钟加工的零件数为=3个,所以甲每分钟比乙多加工5-3=2个,
在60分钟时,甲比乙多加工了(60-20)×2=80(个)零件,所以选项B错误;
当x=128时,y=(128-20)×2=216,所以y的最大值是216,所以选项D正确.
题8(多选题).某食品的保鲜时间t(单位:小时)与存储温度x(单位:℃)满足函数关系且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,则以下四个结论正确的是( )
A.该食品在6 ℃的保鲜时间是8小时
B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少
C.到了此日13时,甲所购买的食品还在保鲜时间内
D.到了此日14时,甲所购买的食品已然过了保鲜时间
【解析】选AD.因为食品的保鲜时间t与储藏温度x满足函数关系式且该食品在4 ℃时保鲜时间是16小时.
所以24k+6=16,即4k+6=4,解得k=-.
所以.
A.当x=6时,t=8,所以该食品在6 ℃的保鲜时间是8小时,故A正确;
B.当x∈[-6,0)时,时间t不变,故B错误;
C.由图象可知,当到此日12小时,温度超过12度,此时的保鲜时间不超过1小时,所以到了此日13时,甲所购买的食品不在保鲜时间内,故C错误;D由C知,D正确.
题9. 英国物理学家和数学家艾萨克·牛顿曾提出了物体在常温环境下温度变化的冷却模型.现把一杯温水放在空气中冷却,假设这杯水从开始冷却,x分钟后物体的温度f(x)满足:
.则从开始冷却,经过5分钟时间这杯水的温度是________(单位:℃).
【思路导引】代入数据,利用对数恒等式运算.
【解析】.
答案:
题9.某种药在病人血液中的含量不低于2克时,它才能起到有效的治疗作用,己知服用m(1≤m≤4,m∈R)个单位的药剂,药剂在血液中的含量y(克)随着时间x(小时)变化的函数关系式近似为y=m·f(x),其中
(1)若病人一次服用3个单位的药剂,则有效治疗时间可达________小时.
(2)若病人第一次服用2个单位的药剂,6个小时后再服用m个单位的药剂,要使接下来的2小时中能够持续有效治疗,则m的最小值为________.
【解析】(1)若病人一次服用3个单位的药剂,则m=3,所以
当0≤x<6时,=3>2,当6≤x≤8时,令≥2,解得x≤,
所以若病人一次服用3个单位的药剂,则有效治疗时间可达小时.
(2)若病人第一次服用2个单位的药剂,则m=2,所以
此时=2,8-x≤8-6=2,所以治疗时间末端为第6小时结束,
因为在治疗时间末端再服用m个单位药剂,
所以6≤x≤8,所以y=,
所以8-x+≥2对于任意x∈[6,8]恒成立,所以m≥ 对于任意x∈[6,8]恒成立,
设g(x)=,x∈[6,8],为开口向上,对称轴为x=4的抛物线,
所以g(x)在[6,8]上单调递增,所以g(x)max=g(8)=,故m≥,
所以m的最小值为.
答案:
题10.某年春季蝗灾波及印度和巴基斯坦,假设蝗虫的日增长率为5%,最初有N0只.则经过______天能达到最初的16 000倍(参考数据:ln 1.05≈0.048 8,ln 1.5≈0.405 5,ln 1 600≈7.377 8,ln 16 000≈9.680 3).
【解析】设过x天能达到最初的16 000倍,
由已知N0(1+0.05)x=16 000N0,
即1.05x=16 000,所以x=≈198.4,
又x∈N,所以过199天能达到最初的16 000倍.
答案:199
题11.因新冠肺炎疫情影响,呼吸机成为紧缺商品,某呼吸机生产企业为了提高产品的产量,投入90万元安装了一台新设备,并立即进行生产,预计使用该设备前n(n∈N+)年的材料费、维修费、人工工资等共为万元,每年的销售收入55万元.设使用该设备前n年的总盈利额为f(n)万元.
(1)写出f(n)关于n的函数关系式,并估计该设备从第几年开始盈利;
(2)使用若干年后,对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以10万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以50万元的价格处理;
问哪种方案处理较为合理?并说明理由.
【解析】(1)由题意得:f(n)=55n-90-=-n2+50n-90.
由f(n)>0,得-n2+50n-90>0,即n2-20n+36<0,解得2<n<18.
由于n∈N+,故该企业从第3年开始盈利;
(2)方案一:总盈利额f(n)=-(n-10)2+160,当n=10时,f(n)max=160.
故方案一总利润160+10=170,此时n=10;
方案二:每年平均利润=20,当且仅当n=6时等号成立.
故方案二总利润6×20+50=170,此时n=6.
比较两种方案,获利都是170万元,但由于第一种方案需要10年,而第二种方案需要6年,故选择第二种方案更合适.
【课堂检测达标】
题12.某种电热水器的水箱盛满水是200升,加热到一定温度可浴用.浴用时,已知每分钟放水34升,在放水的同时注水,t分钟注水2t2升,当水箱内水量达到最小值时,放水自动停止.现假定每人洗浴用水65升,则该热水器一次至多可供几人洗澡( )
A.3人 B.4人 C.5人 D.6人
【解析】选B.水箱内水量y=200+2t2-34t,当t=时,y有最小值,
此时共放水34×=289(升),≈4.4,故至多可供4人洗澡.
题13.心理学家有时使用函数L(t)=A(1-e-kt)来测定一个人在时间t(min)内能够记忆的量L,其中A表示需要记忆的量,k表示记忆率.假设一个学生有200个单词要记忆,心理学家测定在5 min内该学生能够记忆20个单词.则记忆率k所在区间为( )
A. B.
C. D.
【解析】选A.将A=200,t=5,L=20代入L(t)=A(1-e-kt),
则e-5k=,其中y=e-5x单调递减,而,
而y=x-4在(0,+∞)上单调递减,
所以,结合单调性可知,,即,
由e-5×0=e0=1> ,其中y=e-5x为连续函数,
故记忆率k所在区间为 .
题14(多选题).一家货物公司计划租地建造仓库储存货物,经市场调查了解到下列信息:每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费y2(单位:万元)与x成正比,若在距离车站10 km处建仓库,则y1为1万元,y2为4万元,下列结论正确的是( )
A.y1=x (1) B.y2=0.4x C.y1+y2有最小值4 D.y1-y2无最小值
【解析】选BCD.对A,设y1=,由题意知:函数过点(10,4),即k1=10,所以y1=,故A错误;
对B,y2=k2x,,由题意得:函数过点(10,4),即4=10k2,解得k2=0.4,所以y2=0.4x,,故B正确;
对C,y1+y2==4,当且仅当=0.4x,即x=5时等号成立,故C正确;
对D,因为y1-y2=-0.4x在(0,+∞)上单调递减,故y1-y2无最小值,故D正确.
题15(多选题).据某国学者詹姆斯·马丁的测算,近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度.因此,基础教育的任务已不是教会一切人一切知识,而是让一切人学会学习.已知2002年底,人类知识总量为a,假如从2002年底到2012年底是每三年翻一番,从2012年底到2022年底是每一年翻一番,2023年(按365天计算)是每73天翻一番,则下列说法正确的是
A.2008年底人类知识总量是2a B.2012年底人类知识总量是8a ( )
C.2022年底人类知识总量是213a D.2023年底人类知识总量是218a
【解析】选BCD.选项A:2008年底人类知识总量为a×2×2=4a,故A错误,
选项B:2012年底人类知识总量为a×2×2×2=8a,故B正确,
选项C:2022年底人类知识总量为8a×210=213a,故C正确,
选项D:2023年底人类知识总量为213a×25=218a,故D正确.
题16.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份0.8元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸________份.
【解析】设每天从报社买进x(250≤x≤400,x∈N)份报纸时,每月所获利润为y元,具体情况如下表.
项目 数量/份 单价/元 金额/元
买进 30x 2 60x
卖出 20x+10×250 3 60x+7 500
退回 10(x-250) 0.8 8x-2 000
则推销员每月所获得的利润y=[(60x+7 500)+(8x-2 000)]-60x=8x+5500(250≤x≤400,x∈N)
又由y=8x+5 500在[250,400]上单调递增,
所以当x=400时,y取得最大值8 700.
答案:400
题17.某制造商制造并出售圆柱形瓶装的某种饮料,瓶子的底面半径是r,高h=r(单位:cm),一个瓶子的制造成本是0.8πr2分,已知每出售1 mL(注:1 mL=1 cm3)的饮料,制造商可获利0.2分,且制造商能制造的瓶子底面的最大半径为6 cm.记每瓶饮料的利润为f(r),则f(3)=________,其实际意义是____________.
【解析】f(r)=0.2·πr2·r-0.8πr2=-0.8πr2(0<r≤6),
故f(3)=7.2 π-7.2 π=0.
表示当瓶子底面半径为3 cm时,利润为0.
答案:0 当瓶子底面半径为3 cm时,利润为0
题18.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=-48x+8 000,已知此生产线年产量最大为230吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本P(年总成本除以年产量)最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,且生产的产品全部售完,那么当年产量为多少吨时,年总利润可以获得最大?最大利润是多少?
【解析】(1)y=-48x+8 000,0<x≤230.
所以P==32,当且仅当x=200时取等号.
所以年产量为200吨时,生产每吨产品的平均成本P最低,最低成本为32万元.
(2)设利润为z万元,
则z=40x-y=40x-+48x-8 000
=-x2+88x-8 000=-(x-220)2+1 680,
即年产量为220吨时,利润最大为1 680万元.
题19.销售甲、乙两种商品所得利润分别是y1,y2万元,它们与投入资金x万元的关系分别为y1=m+a,y2=bx(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示.
(1)求函数y1与y2的解析式;
(2)若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值.
【解析】(1)由题意解得m=2,a=-2,故y1=2-2.
又由题意8b=4得b=,故y2=x.
(2)设销售甲商品投入资金x万元,利润为y万元,则乙投入(10-x)万元.
由(1)得y=2-2+=2-x+3,0≤x≤10.
令=t,则1≤t≤且x=t2-1,
故y=2t-+3=-t2+2t+=-(t-2)2+,1≤t≤,
当t=2即x=3时,y取最大值.
答:该商场所获利润的最大值为万元.
【综合突破拔高】
题20. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如表所示的关系.
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p元,则x,p分别为( )
A.35,225 B.40,300 C.45,350 D.45,400
【解析】选B.由表格可知,x与y满足一次函数关系,设y=ax+b(a≠0),把点(30,60)和点(40,30)代入得: 解得
所以y=-3x+150 (x≥30),所以销售利润p=y(x-30)=-3x2+240x-4 500(x≥30),所以当x=40时,p的值最大,最大值为300.
题21.某商场对顾客实行购物优惠活动,规定一次购物:
(1)如不超过200元,则不予优惠;
(2)如超过200元但不超过500元,则全款按9折优惠;
(3)如超过500元,其中500元按9折给予优惠,超过500的部分按8折给予优惠.
某人两次去购物,分别付款168元和423元,若他只去一次购买同样价格的商品,则应付款( )
A.472.8元 B.510.4元 C.522.8元 D.560.4元
【解析】选D.购物500元应付款500×0.9=450(元),
设第二次购物的原价为a,则200<a<500,故0.9a=423,解得a=470.
故两次购物原价为168+470=638(元).
若一次购物638元,则应付款500×0.9+138×0.8=560.4(元).
题22.已知样本中碳14的质量N随时间t(年)的衰变规律满足:N=N0·(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log2 3≈1.6,log2 5≈2.3)
A.3440年 B.4010年
C.4580年 D.5160年
【解析】选B.由题意,可得0.6N0=N0·,
即=0.6=5 (3),两边取以2为底数的对数,
可得=log23-log25≈1.6-2.3=-0.7,
所以t≈0.7×5730=4011年.
题23. 8月到11月这四个月的某产品价格的市场平均价f(x)(单位:元/千克)与时间x(单位:月份)的数据如表
x 8 9 10 11
f(x) 28.00 33.99 36.00 34.02
现有三种函数模型:①f(x)=bx+a;②f(x)=ax2+bx+c;③f(x)=+a,找出你认为最适合的函数模型,并估计2020年12月份的该产品市场平均价( )
A.②,28元/千克
B.①,25元/千克
C.②,23元/千克
D.③,21元/千克
【解析】选A.因为f(x)的值随x的值先增后减,所以选f(x)=ax2+bx+c最合适.
第二组数据近似为(9,34),第四组近似为(11,34),得f(x)图象的对称轴为x=10,
故f(12)=f(8)=28.
题24.声强级L1(单位:dB)与声强I的函数关系式为:L1=10lg.若普通列车的声强级是95 dB,高速列车的声强级为45 dB,则普通列车的声强是高速列车声强的( )
A.106倍 B.105倍 C.104倍 D.103倍
【解析】选B.设普通列车的声强为I1,高速列车的声强为I2,
因为普通列车的声强级是95 dB,高速列车的声强级为45 dB,
所以95=10lg,45=10lg,
95=10lg=10,解得-2.5=lg I1,
所以I1=10-2.5,45=10lg =10,解得-7.5=lg I2,所以I2=10-7.5,
两式相除得=105,则普通列车的声强是高速列车声强的105倍.
题25(多选题). “双11”购物节中,某电商对顾客实行购物优惠活动,规定一次购物付款总额满一定额度,可以给予优惠:
(1)如果购物总额不超过50元,则不给予优惠;
(2)如果购物总额超过50元但不超过100元,可以使用一张5元优惠券;
(3)如果购物总额超过100元但不超过300元,则按标价给予9折优惠;
(4)如果购物总额超过300元,其中300元内的按第(3)条给予优惠,超过300元的部分给予8折优惠.
某人购买了部分商品,则下列说法正确的是 ( )
A.如果购物总额为78元,则应付款为73元 B.如果购物总额为228元,则应付款为205.2元
C.如果购物总额为368元,则应付款为294.4元
D.如果购物时一次性全部付款442.8元,则购物总额为516元
【解析】选ABD.如果购物总额为78元,满足超过50元但不超过100元,可以使用一张5元优惠券,则应付款为73元,故A正确;如果购物总额为228元,超过100元但不超过300元,则应付款为228×0.9=205.2元,故B正确;如果购物总额为368元,购物总额超过300元,则应付款为300×0.9+68×0.8=324.4元,故C错误;如果购物时一次性全部付款442.8元,说明购物总额超过300元,设购物总额为x元,则300×0.9+(x-300)×0.8=442.8,解得x=516元,故D正确.
题26(多选题).某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用y1(千元),乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示,则下列说法正确的是 ( )
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的总费用y1与证书数量x之间的函数关系式为y1=0.5x+1
C.若该单位需印制证书数量为8千个,则该单位选择甲厂更节省费用
D.当印制证书数量超过2千个时,乙厂的总费用y2与证书数量x之间的函数关系式为y2=x+
【解析】选ABD.对于选项A:由图可知甲厂制版费为1千元,印刷费平均每个为=0.5(元),所以选项A正确,对于选项B:设甲厂的总费用y1与证书数量x之间的函数关系式为y1=kx+b(k≠0),
则解得所以y1=0.5x+1,所以选项B正确,
对于选项C:由图象可知,当印制证书数量超过6千个时,乙厂费用少于甲厂费用,
所以若该单位需印制证书数量为8千个,则该单位选择乙厂更节省费用,所以选项C错误,
对于选项D:当印制证书数量超过2千个时,
设乙厂的总费用y2与证书数量x之间的函数关系式为y2=ax+c(a≠0),代入点(2,3)和点(6,4)得
解得所以y2=x+,所以选项D正确.
题27.某项研究表明:在考虑行车安全的情况下,某路段车流量F(单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v(假设车辆以相同速度v行驶,单位:米/秒)、平均车长l(单位:米)的值有关,其公式为F=.
(1)如果不限定车型,l=6.05,则最大车流量为________辆/小时;
(2)如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加______辆/小时.
【解析】(1)F=
因为=22,当v=11时分母取最小值,所以F=≤1 900,故最大车流量为:1 900辆/小时;
(2)F=,因为,所以F≤2 000,2 000-1 900=100(辆/小时),故最大车流量比(1)中的最大车流量增加100辆/小时.
答案:(1)1 900 (2)100
题28.某种细菌经30分钟数量变为原来的2倍,且该种细菌的繁殖规律为y=ekt,其中k为常数,t表示时间(单位:小时),y表示繁殖后细菌总个数,经过5小时,1个细菌通过繁殖个数变为________.
【解析】由题意知,当t=时,y=2,即2=,所以k=2ln 2,
所以y=.当t=5时,y==210=1 024.
即经过5小时,1个细菌通过繁殖个数变为1 024.
答案:1 024
题29.已知14C的半衰期为5 730年(是指经过5 730年后,14C的残余量占原始量的一半).设14C的原始量为a,经过x年后的残余量为b,残余量b与原始量a的关系如下:b=ae-kx,其中x表示经过的时间,k为一个常数.现测得湖南长沙马王堆汉墓女尸出土时14C的残余量约占原始量的76.7%.请你推断一下马王堆汉墓的大致年代为距今________年.(已知log20.767≈-0.4,ln 2≈0.69)
【解析】由题意可知,当x=5 730时ae-5 730k=a,解得k=.
现测得湖南长沙马王堆汉墓女尸出土时14C的残余量约占原始量的76.7%.
所以76.7%=,得ln 0.767=-x,
x=-5 730×=-5 730×log20.767≈2 292.
答案:2 292
题30.为节约能源,倡导绿色环保,某主题公园有60辆电动观光车供租赁使用,管理这些电动观光车的费用是每日120元.根据经验,若每辆电动观光车的日租金不超过5元,则电动观光车可以全部租出;若超过5元,则每超过1元,租不出去的电动观光车就增加2辆.为了便于结算,每辆电动观光车的日租金x(元)只取整数,并且要求出租电动观光车一日的收入必须高于这一日的管理费用,用y(元)表示出租电动观光车的日净收入(即一日出租电动观光车的总收入减去管理费用后的所得).
(1)求y关于x的解析式及其定义域;(2)当每辆电动观光车的日租金为多少元时,才能使一日的净收入最多?
【解析】(1)当x≤5时,y=60x-120,令60x-120>0,得x>2,因为x∈,所以3≤x≤5(x∈).
当x>5时,y=[60-2(x-5)]x-120=-2x2+70x-120,令-2x2+70x-120>0,即x2-35x+60<0,
上述不等式的整数解为2≤x≤33(x∈N*),所以5综上,y=
(2)对于y=60x-120,3≤x≤5,x∈,显然当x=5时,ymax=180.
对于y=-2x2+70x-120=,5180,所以当每辆电动观光车的日租金为17元或18元时,才能使一日的净收入最多.
题31. 小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为W(x)万元.在年产量不足万件时,(万元);在年产量不小于8万件时, (万元).每件产品售价为5元.通过市场分析,小王生产的商 品当年能全部售完.写出年利润L(x)(万元)关于年产量x(万件)的函数解析式.(注:年利润=年销售收入-固定成本-流动成本)
【解析】因为每件产品售价为5元,则x万件产品的销售收入为5x万元,依题意得:
当0当x≥8时,.
所以
题32.围建一个面积为360的矩形场地,要求矩形场地的一面利用30 m的旧墙(利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m).
分别写出矩形场地的另一边长C(单位:m)、旧墙维修费用P(单位:元)、新墙的造价R(单位:元)、建设矩形场地的总费用L(单位:元)关于利用旧墙的长度x(单位:m)的函数关系式.
【解析】矩形场地的另一边长C与利用的旧墙的长度x的关系式为.
旧墙的维修费用P与利用的旧墙的长度x的关系式为.
新墙的造价R与利用的旧墙的长度x的关系式为
总的建造费用L与利用的旧墙的长度x的关系式为
题33.运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择,它们的速度分别为60千米/小时、120千米/小时,500千米/小时,每千米的运费分别为:20元、10元、50元.这批海鲜在运输过程中每小时的损耗为m元(m>0),运输的路程为s(千米).设用汽车、火车、飞机三种运输工具运输时各自的总费用(包括运费和损耗费)分别为y1(元),y2(元),y3(元).
(1)请分别写出y1,y2,y3的表达式;
(2)试确定使用哪种运输工具总费用最省.
【思路导引】(1)运输总费用=每千米的费用×.
(2)利用y1,y2,y3的表达式比较费用的大小.
【解析】(1).
(2)因为m>0,s>0,故20s>10s, ,
所以y1>y2恒成立,故只需比较y2与y3的大小关系即可,
令,
故当,即时,f(s)>0,
即y2当,即时,f(s)<0,
即y2>y3,此时选择飞机运输费用最省;
当,即时,f(s)=0,
即y2=y3,此时选择火车或飞机运输费用最省.
题34.据调查:人类在能源利用与森林砍伐中使CO2浓度增加.据测,2015年,2016年,2017年大气中的CO2浓度分别比2014年增加了1个单位,3个单位,6个单位.若用一个函数模拟每年CO2浓度增加的单位数y与年份增加数x的关系,模拟函数可选用二次函数f(x)=px2+qx+r(其中p,q,r为常数)或函数g(x)=a·bx+c(其中a,b,c为常数),又知2018年大气中的CO2浓度比2014年增加了16.5个单位,请问用以上哪个函数作模拟函数较好
【思路导引】首先根据已知条件确定两个模拟函数的解析式,再利用2018年的测量值检验模拟效果.
【解析】若以f(x)=px2+qx+r作模拟函数,
则依题意得:解得所以.
若以作模拟函数,
则解得所以.
利用f(x),g(x)对2018年CO2浓度作估算,则其数值分别为:
f(4)=10个单位,g(4)=10.5个单位,因为|f(4)-16.5|>|g(4)-16.5|,
所以作模拟函数与2018年的实际数据较为接近,故用作模拟函数较好.
- 0 -
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握解答函数应用题的操作步骤;
2.掌握应用问题中的变量关系;
3.会利用函数模型解决实际问题;
4.理解并掌握实际问题中函数模型的选择问题(数学建模).
本节重点难点
重点:利用函数模型解决实际问题;
难点:实际问题中函数模型的选择问题(数学建模).
学科素养目标
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
教学过程赏析
基础知识积累
解决函数应用问题的一般程序是:
审题,设未知量;
寻找等量关系;
列出方程;
解方程;
验根或证明;
结论或作答.
【课前基础演练】
题1. 某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系 (e=2.718…为自然对数的底数,k,b为常数),若该食品在0 ℃时的保鲜时间是192小时,在22 ℃时的保鲜时间是48小时,则该食品在33 ℃时的保鲜时间是____小时 ( )
A.22 B.23 C.24 D.33
题2.据报道,全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度,设2018年北冰洋冬季冰雪覆盖面积为m,则从2018年起,x年后北冰洋冬季冰雪覆盖面积y与x的函数关系式是( )
A.y=
B.y=
C.y=0.9550-x·m
D.y=(1-0.0550-x)·m
题3.某特种冰箱的食物保鲜时间y(单位:小时)与设置储存温度x(单位:℃)近似满足函数关系y=3kx+b(k,b为常数),若设置储存温度0 ℃的保鲜时间是288小时,设置储存温度5 ℃的保鲜时间是144小时,则设置储存温度15 ℃的保鲜时间近似是( )
A.36小时 B.48小时
C.60小时 D.72小时
题4.光线通过一块玻璃,强度要损失10%.设光线原来的强度为k,通过x块这样的玻璃以后强度为y,则经过x块这样的玻璃后光线强度为,那么至少通过____块这样的玻璃,光线强度能减弱到原来的以下() ( )
A.12 B.13 C.14 D.15
题5.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是( )
A.y=0.2x B.y=0.1(x2+2x) C.y= D.y=0.2+log16x
题6.因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面3个折线图中,所有可以反映这种物资每份价格(单位:万元)的变化情况的是( )
A.①② B.①③ C.②③ D.③
题7(多选题).甲乙两人各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为12,B点坐标为(20,0),C点横坐标为128.则下面说法中正确的是( )
A.甲每分钟加工的零件数量是5个
B.在60分钟时,甲比乙多加工了120个零件
C.D点的横坐标是200
D.y的最大值是216
题8(多选题).某食品的保鲜时间t(单位:小时)与存储温度x(单位:℃)满足函数关系且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,则以下四个结论正确的是( )
A.该食品在6 ℃的保鲜时间是8小时
B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少
C.到了此日13时,甲所购买的食品还在保鲜时间内
D.到了此日14时,甲所购买的食品已然过了保鲜时间
题9. 英国物理学家和数学家艾萨克·牛顿曾提出了物体在常温环境下温度变化的冷却模型.现把一杯温水放在空气中冷却,假设这杯水从开始冷却,x分钟后物体的温度f(x)满足:
.则从开始冷却,经过5分钟时间这杯水的温度是________(单位:℃).
题9.某种药在病人血液中的含量不低于2克时,它才能起到有效的治疗作用,己知服用m(1≤m≤4,m∈R)个单位的药剂,药剂在血液中的含量y(克)随着时间x(小时)变化的函数关系式近似为y=m·f(x),其中
(1)若病人一次服用3个单位的药剂,则有效治疗时间可达________小时.
(2)若病人第一次服用2个单位的药剂,6个小时后再服用m个单位的药剂,要使接下来的2小时中能够持续有效治疗,则m的最小值为________.
题10.某年春季蝗灾波及印度和巴基斯坦,假设蝗虫的日增长率为5%,最初有N0只.则经过______天能达到最初的16 000倍(参考数据:ln 1.05≈0.048 8,ln 1.5≈0.405 5,ln 1 600≈7.377 8,ln 16 000≈9.680 3).
题11.因新冠肺炎疫情影响,呼吸机成为紧缺商品,某呼吸机生产企业为了提高产品的产量,投入90万元安装了一台新设备,并立即进行生产,预计使用该设备前n(n∈N+)年的材料费、维修费、人工工资等共为万元,每年的销售收入55万元.设使用该设备前n年的总盈利额为f(n)万元.
(1)写出f(n)关于n的函数关系式,并估计该设备从第几年开始盈利;
(2)使用若干年后,对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以10万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以50万元的价格处理;
问哪种方案处理较为合理?并说明理由.
【课堂检测达标】
题12.某种电热水器的水箱盛满水是200升,加热到一定温度可浴用.浴用时,已知每分钟放水34升,在放水的同时注水,t分钟注水2t2升,当水箱内水量达到最小值时,放水自动停止.现假定每人洗浴用水65升,则该热水器一次至多可供几人洗澡( )
A.3人 B.4人 C.5人 D.6人
题13.心理学家有时使用函数L(t)=A(1-e-kt)来测定一个人在时间t(min)内能够记忆的量L,其中A表示需要记忆的量,k表示记忆率.假设一个学生有200个单词要记忆,心理学家测定在5 min内该学生能够记忆20个单词.则记忆率k所在区间为( )
A. B.
C. D.
题14(多选题).一家货物公司计划租地建造仓库储存货物,经市场调查了解到下列信息:每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费y2(单位:万元)与x成正比,若在距离车站10 km处建仓库,则y1为1万元,y2为4万元,下列结论正确的是( )
A.y1=x (1) B.y2=0.4x C.y1+y2有最小值4 D.y1-y2无最小值
题15(多选题).据某国学者詹姆斯·马丁的测算,近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度.因此,基础教育的任务已不是教会一切人一切知识,而是让一切人学会学习.已知2002年底,人类知识总量为a,假如从2002年底到2012年底是每三年翻一番,从2012年底到2022年底是每一年翻一番,2023年(按365天计算)是每73天翻一番,则下列说法正确的是
A.2008年底人类知识总量是2a B.2012年底人类知识总量是8a ( )
C.2022年底人类知识总量是213a D.2023年底人类知识总量是218a
题16.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份0.8元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸________份.
题17.某制造商制造并出售圆柱形瓶装的某种饮料,瓶子的底面半径是r,高h=r(单位:cm),一个瓶子的制造成本是0.8πr2分,已知每出售1 mL(注:1 mL=1 cm3)的饮料,制造商可获利0.2分,且制造商能制造的瓶子底面的最大半径为6 cm.记每瓶饮料的利润为f(r),则f(3)=________,其实际意义是____________.
题18.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=-48x+8 000,已知此生产线年产量最大为230吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本P(年总成本除以年产量)最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,且生产的产品全部售完,那么当年产量为多少吨时,年总利润可以获得最大?最大利润是多少?
题19.销售甲、乙两种商品所得利润分别是y1,y2万元,它们与投入资金x万元的关系分别为y1=m+a,y2=bx(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示.
(1)求函数y1与y2的解析式;
(2)若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值.
【综合突破拔高】
题20. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如表所示的关系.
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p元,则x,p分别为( )
A.35,225 B.40,300 C.45,350 D.45,400
题21.某商场对顾客实行购物优惠活动,规定一次购物:
(1)如不超过200元,则不予优惠;
(2)如超过200元但不超过500元,则全款按9折优惠;
(3)如超过500元,其中500元按9折给予优惠,超过500的部分按8折给予优惠.
某人两次去购物,分别付款168元和423元,若他只去一次购买同样价格的商品,则应付款( )
A.472.8元 B.510.4元 C.522.8元 D.560.4元
题22.已知样本中碳14的质量N随时间t(年)的衰变规律满足:N=N0·(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log2 3≈1.6,log2 5≈2.3)
A.3440年 B.4010年
C.4580年 D.5160年
题23. 8月到11月这四个月的某产品价格的市场平均价f(x)(单位:元/千克)与时间x(单位:月份)的数据如表
x 8 9 10 11
f(x) 28.00 33.99 36.00 34.02
现有三种函数模型:①f(x)=bx+a;②f(x)=ax2+bx+c;③f(x)=+a,找出你认为最适合的函数模型,并估计2020年12月份的该产品市场平均价( )
A.②,28元/千克
B.①,25元/千克
C.②,23元/千克
D.③,21元/千克
题24.声强级L1(单位:dB)与声强I的函数关系式为:L1=10lg.若普通列车的声强级是95 dB,高速列车的声强级为45 dB,则普通列车的声强是高速列车声强的( )
A.106倍 B.105倍 C.104倍 D.103倍
题25(多选题). “双11”购物节中,某电商对顾客实行购物优惠活动,规定一次购物付款总额满一定额度,可以给予优惠:
(1)如果购物总额不超过50元,则不给予优惠;
(2)如果购物总额超过50元但不超过100元,可以使用一张5元优惠券;
(3)如果购物总额超过100元但不超过300元,则按标价给予9折优惠;
(4)如果购物总额超过300元,其中300元内的按第(3)条给予优惠,超过300元的部分给予8折优惠.
某人购买了部分商品,则下列说法正确的是 ( )
A.如果购物总额为78元,则应付款为73元 B.如果购物总额为228元,则应付款为205.2元
C.如果购物总额为368元,则应付款为294.4元
D.如果购物时一次性全部付款442.8元,则购物总额为516元
题26(多选题).某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用y1(千元),乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示,则下列说法正确的是 ( )
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的总费用y1与证书数量x之间的函数关系式为y1=0.5x+1
C.若该单位需印制证书数量为8千个,则该单位选择甲厂更节省费用
D.当印制证书数量超过2千个时,乙厂的总费用y2与证书数量x之间的函数关系式为y2=x+
题27.某项研究表明:在考虑行车安全的情况下,某路段车流量F(单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v(假设车辆以相同速度v行驶,单位:米/秒)、平均车长l(单位:米)的值有关,其公式为F=.
(1)如果不限定车型,l=6.05,则最大车流量为________辆/小时;
(2)如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加______辆/小时.
题28.某种细菌经30分钟数量变为原来的2倍,且该种细菌的繁殖规律为y=ekt,其中k为常数,t表示时间(单位:小时),y表示繁殖后细菌总个数,经过5小时,1个细菌通过繁殖个数变为________.
题29.已知14C的半衰期为5 730年(是指经过5 730年后,14C的残余量占原始量的一半).设14C的原始量为a,经过x年后的残余量为b,残余量b与原始量a的关系如下:b=ae-kx,其中x表示经过的时间,k为一个常数.现测得湖南长沙马王堆汉墓女尸出土时14C的残余量约占原始量的76.7%.请你推断一下马王堆汉墓的大致年代为距今________年.(已知log20.767≈-0.4,ln 2≈0.69)
题30.为节约能源,倡导绿色环保,某主题公园有60辆电动观光车供租赁使用,管理这些电动观光车的费用是每日120元.根据经验,若每辆电动观光车的日租金不超过5元,则电动观光车可以全部租出;若超过5元,则每超过1元,租不出去的电动观光车就增加2辆.为了便于结算,每辆电动观光车的日租金x(元)只取整数,并且要求出租电动观光车一日的收入必须高于这一日的管理费用,用y(元)表示出租电动观光车的日净收入(即一日出租电动观光车的总收入减去管理费用后的所得).
(1)求y关于x的解析式及其定义域;(2)当每辆电动观光车的日租金为多少元时,才能使一日的净收入最多?
题31. 小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为W(x)万元.在年产量不足万件时,(万元);在年产量不小于8万件时, (万元).每件产品售价为5元.通过市场分析,小王生产的商 品当年能全部售完.写出年利润L(x)(万元)关于年产量x(万件)的函数解析式.(注:年利润=年销售收入-固定成本-流动成本)
题32.围建一个面积为360的矩形场地,要求矩形场地的一面利用30 m的旧墙(利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m).
分别写出矩形场地的另一边长C(单位:m)、旧墙维修费用P(单位:元)、新墙的造价R(单位:元)、建设矩形场地的总费用L(单位:元)关于利用旧墙的长度x(单位:m)的函数关系式.
题33.运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择,它们的速度分别为60千米/小时、120千米/小时,500千米/小时,每千米的运费分别为:20元、10元、50元.这批海鲜在运输过程中每小时的损耗为m元(m>0),运输的路程为s(千米).设用汽车、火车、飞机三种运输工具运输时各自的总费用(包括运费和损耗费)分别为y1(元),y2(元),y3(元).
(1)请分别写出y1,y2,y3的表达式;
(2)试确定使用哪种运输工具总费用最省.
题34.据调查:人类在能源利用与森林砍伐中使CO2浓度增加.据测,2015年,2016年,2017年大气中的CO2浓度分别比2014年增加了1个单位,3个单位,6个单位.若用一个函数模拟每年CO2浓度增加的单位数y与年份增加数x的关系,模拟函数可选用二次函数f(x)=px2+qx+r(其中p,q,r为常数)或函数g(x)=a·bx+c(其中a,b,c为常数),又知2018年大气中的CO2浓度比2014年增加了16.5个单位,请问用以上哪个函数作模拟函数较好
编号:055 课题: 8.2.2 函数的实际应用
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握解答函数应用题的操作步骤;
2.掌握应用问题中的变量关系;
3.会利用函数模型解决实际问题;
4.理解并掌握实际问题中函数模型的选择问题(数学建模).
本节重点难点
重点:利用函数模型解决实际问题;
难点:实际问题中函数模型的选择问题(数学建模).
学科素养目标
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
教学过程赏析
基础知识积累
解决函数应用问题的一般程序是:
审题,设未知量;
寻找等量关系;
列出方程;
解方程;
验根或证明;
结论或作答.
【课前基础演练】
题1. 某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系 (e=2.718…为自然对数的底数,k,b为常数),若该食品在0 ℃时的保鲜时间是192小时,在22 ℃时的保鲜时间是48小时,则该食品在33 ℃时的保鲜时间是____小时 ( )
A.22 B.23 C.24 D.33
【思路导引】可通过整体代入法求解.
【解析】选C.某食品的保鲜时间y(单位:小时)与储存温度x(单位: ℃)满足函数关系 (e=2.718…为自然对数的底数,k,b为常数),该食品在0 ℃时的保鲜时间是192小时,在22 ℃时的保鲜时间是48小时,所以解得,
所以该食品在33 ℃时的保鲜时间:(小时).
题2.据报道,全球变暖使北冰洋冬季冰雪覆盖面积在最近50年内减少了5%,如果按此速度,设2018年北冰洋冬季冰雪覆盖面积为m,则从2018年起,x年后北冰洋冬季冰雪覆盖面积y与x的函数关系式是( )
A.y=
B.y=
C.y=0.9550-x·m
D.y=(1-0.0550-x)·m
【解析】选A.设北冰洋每年冬季冰雪覆盖面积为上一年的q%.由题意可知(q%)50=0.95,所以q%=,所以从2018年起,x年后北冰洋冬季冰雪覆盖面积y与x的函数关系式为y=·m.
题3.某特种冰箱的食物保鲜时间y(单位:小时)与设置储存温度x(单位:℃)近似满足函数关系y=3kx+b(k,b为常数),若设置储存温度0 ℃的保鲜时间是288小时,设置储存温度5 ℃的保鲜时间是144小时,则设置储存温度15 ℃的保鲜时间近似是( )
A.36小时 B.48小时
C.60小时 D.72小时
【解析】选A.由题意可知
所以35k+b=35k×3b=144,所以35k=,
所以当x=15时,y=315k+b=315k×3b=(35k)3×3b=×288=×288=36,故设置储存温度15 ℃的保鲜时间近似是36小时.
题4.光线通过一块玻璃,强度要损失10%.设光线原来的强度为k,通过x块这样的玻璃以后强度为y,则经过x块这样的玻璃后光线强度为,那么至少通过____块这样的玻璃,光线强度能减弱到原来的以下() ( )
A.12 B.13 C.14 D.15
【解析】选C.光线经过x块玻璃后,强度变为.由题意,即,
两边同取对数,可得,因为,
所以,因为,所以.
即至少通过14块玻璃.
题5.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是( )
A.y=0.2x B.y=0.1(x2+2x) C.y= D.y=0.2+log16x
【解析】选C.因为三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,所以可以看出来不是线性增加,故选项A不符合题意;
对于选项B:把x=1,2,3分别代入解析式中得y=0.3,0.8,1.5,不符合题意;
对于选项C:把x=1,2,3分别代入解析式中得y=0.2,0.4,0.8,符合题意,
对于选项D:把x=1代入解析式中,得y=0.2,把x=2代入解析式中,得y=0.2+log162=0.45,把x=3代入解析式中,得y=0.2+log163=0.2+log23<0.2+log24=0.7,跟选项C来比,选项C更近似.
题6.因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面3个折线图中,所有可以反映这种物资每份价格(单位:万元)的变化情况的是( )
A.①② B.①③ C.②③ D.③
【解析】选B.设公司每月1日用于购买某种物资的金额为a万元.
题图①中四次购买的物资为,5月1日一次卖出物资得到,公司盈利,故①正确;
题图②中四次购买的物资为,5月1日一次卖出物资得到,公司亏损,故②错误;
题图③中四次购买的物资为,5月1日一次卖出物资得到,公司盈利,故③正确.
题7(多选题).甲乙两人各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为12,B点坐标为(20,0),C点横坐标为128.则下面说法中正确的是( )
A.甲每分钟加工的零件数量是5个
B.在60分钟时,甲比乙多加工了120个零件
C.D点的横坐标是200
D.y的最大值是216
【解析】选ACD.根据题意,甲一共加工的时间为(12-0)+(128-20)=120分钟,
一共加工了600个零件,则甲每分钟加工的数量是=5(个),所以选项A正确;
设D的坐标为(t,0),在区间(128,t)和(12,20)上,都是乙在加工,则直线AB和CD的斜率相等,则有∠ABO=∠CDB,在区间(20,128)和(0,12)上,甲乙同时加工,同理可得∠AOB=∠CBD,则△AOB∽△CBD,则有,解得t=200,即点D的坐标是(200,0),所以选项C正确;由题得乙每分钟加工的零件数为=3个,所以甲每分钟比乙多加工5-3=2个,
在60分钟时,甲比乙多加工了(60-20)×2=80(个)零件,所以选项B错误;
当x=128时,y=(128-20)×2=216,所以y的最大值是216,所以选项D正确.
题8(多选题).某食品的保鲜时间t(单位:小时)与存储温度x(单位:℃)满足函数关系且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,则以下四个结论正确的是( )
A.该食品在6 ℃的保鲜时间是8小时
B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少
C.到了此日13时,甲所购买的食品还在保鲜时间内
D.到了此日14时,甲所购买的食品已然过了保鲜时间
【解析】选AD.因为食品的保鲜时间t与储藏温度x满足函数关系式且该食品在4 ℃时保鲜时间是16小时.
所以24k+6=16,即4k+6=4,解得k=-.
所以.
A.当x=6时,t=8,所以该食品在6 ℃的保鲜时间是8小时,故A正确;
B.当x∈[-6,0)时,时间t不变,故B错误;
C.由图象可知,当到此日12小时,温度超过12度,此时的保鲜时间不超过1小时,所以到了此日13时,甲所购买的食品不在保鲜时间内,故C错误;D由C知,D正确.
题9. 英国物理学家和数学家艾萨克·牛顿曾提出了物体在常温环境下温度变化的冷却模型.现把一杯温水放在空气中冷却,假设这杯水从开始冷却,x分钟后物体的温度f(x)满足:
.则从开始冷却,经过5分钟时间这杯水的温度是________(单位:℃).
【思路导引】代入数据,利用对数恒等式运算.
【解析】.
答案:
题9.某种药在病人血液中的含量不低于2克时,它才能起到有效的治疗作用,己知服用m(1≤m≤4,m∈R)个单位的药剂,药剂在血液中的含量y(克)随着时间x(小时)变化的函数关系式近似为y=m·f(x),其中
(1)若病人一次服用3个单位的药剂,则有效治疗时间可达________小时.
(2)若病人第一次服用2个单位的药剂,6个小时后再服用m个单位的药剂,要使接下来的2小时中能够持续有效治疗,则m的最小值为________.
【解析】(1)若病人一次服用3个单位的药剂,则m=3,所以
当0≤x<6时,=3>2,当6≤x≤8时,令≥2,解得x≤,
所以若病人一次服用3个单位的药剂,则有效治疗时间可达小时.
(2)若病人第一次服用2个单位的药剂,则m=2,所以
此时=2,8-x≤8-6=2,所以治疗时间末端为第6小时结束,
因为在治疗时间末端再服用m个单位药剂,
所以6≤x≤8,所以y=,
所以8-x+≥2对于任意x∈[6,8]恒成立,所以m≥ 对于任意x∈[6,8]恒成立,
设g(x)=,x∈[6,8],为开口向上,对称轴为x=4的抛物线,
所以g(x)在[6,8]上单调递增,所以g(x)max=g(8)=,故m≥,
所以m的最小值为.
答案:
题10.某年春季蝗灾波及印度和巴基斯坦,假设蝗虫的日增长率为5%,最初有N0只.则经过______天能达到最初的16 000倍(参考数据:ln 1.05≈0.048 8,ln 1.5≈0.405 5,ln 1 600≈7.377 8,ln 16 000≈9.680 3).
【解析】设过x天能达到最初的16 000倍,
由已知N0(1+0.05)x=16 000N0,
即1.05x=16 000,所以x=≈198.4,
又x∈N,所以过199天能达到最初的16 000倍.
答案:199
题11.因新冠肺炎疫情影响,呼吸机成为紧缺商品,某呼吸机生产企业为了提高产品的产量,投入90万元安装了一台新设备,并立即进行生产,预计使用该设备前n(n∈N+)年的材料费、维修费、人工工资等共为万元,每年的销售收入55万元.设使用该设备前n年的总盈利额为f(n)万元.
(1)写出f(n)关于n的函数关系式,并估计该设备从第几年开始盈利;
(2)使用若干年后,对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以10万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以50万元的价格处理;
问哪种方案处理较为合理?并说明理由.
【解析】(1)由题意得:f(n)=55n-90-=-n2+50n-90.
由f(n)>0,得-n2+50n-90>0,即n2-20n+36<0,解得2<n<18.
由于n∈N+,故该企业从第3年开始盈利;
(2)方案一:总盈利额f(n)=-(n-10)2+160,当n=10时,f(n)max=160.
故方案一总利润160+10=170,此时n=10;
方案二:每年平均利润=20,当且仅当n=6时等号成立.
故方案二总利润6×20+50=170,此时n=6.
比较两种方案,获利都是170万元,但由于第一种方案需要10年,而第二种方案需要6年,故选择第二种方案更合适.
【课堂检测达标】
题12.某种电热水器的水箱盛满水是200升,加热到一定温度可浴用.浴用时,已知每分钟放水34升,在放水的同时注水,t分钟注水2t2升,当水箱内水量达到最小值时,放水自动停止.现假定每人洗浴用水65升,则该热水器一次至多可供几人洗澡( )
A.3人 B.4人 C.5人 D.6人
【解析】选B.水箱内水量y=200+2t2-34t,当t=时,y有最小值,
此时共放水34×=289(升),≈4.4,故至多可供4人洗澡.
题13.心理学家有时使用函数L(t)=A(1-e-kt)来测定一个人在时间t(min)内能够记忆的量L,其中A表示需要记忆的量,k表示记忆率.假设一个学生有200个单词要记忆,心理学家测定在5 min内该学生能够记忆20个单词.则记忆率k所在区间为( )
A. B.
C. D.
【解析】选A.将A=200,t=5,L=20代入L(t)=A(1-e-kt),
则e-5k=,其中y=e-5x单调递减,而,
而y=x-4在(0,+∞)上单调递减,
所以,结合单调性可知,,即,
由e-5×0=e0=1> ,其中y=e-5x为连续函数,
故记忆率k所在区间为 .
题14(多选题).一家货物公司计划租地建造仓库储存货物,经市场调查了解到下列信息:每月土地占地费y1(单位:万元)与仓库到车站的距离x(单位:km)成反比,每月库存货物费y2(单位:万元)与x成正比,若在距离车站10 km处建仓库,则y1为1万元,y2为4万元,下列结论正确的是( )
A.y1=x (1) B.y2=0.4x C.y1+y2有最小值4 D.y1-y2无最小值
【解析】选BCD.对A,设y1=,由题意知:函数过点(10,4),即k1=10,所以y1=,故A错误;
对B,y2=k2x,,由题意得:函数过点(10,4),即4=10k2,解得k2=0.4,所以y2=0.4x,,故B正确;
对C,y1+y2==4,当且仅当=0.4x,即x=5时等号成立,故C正确;
对D,因为y1-y2=-0.4x在(0,+∞)上单调递减,故y1-y2无最小值,故D正确.
题15(多选题).据某国学者詹姆斯·马丁的测算,近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度.因此,基础教育的任务已不是教会一切人一切知识,而是让一切人学会学习.已知2002年底,人类知识总量为a,假如从2002年底到2012年底是每三年翻一番,从2012年底到2022年底是每一年翻一番,2023年(按365天计算)是每73天翻一番,则下列说法正确的是
A.2008年底人类知识总量是2a B.2012年底人类知识总量是8a ( )
C.2022年底人类知识总量是213a D.2023年底人类知识总量是218a
【解析】选BCD.选项A:2008年底人类知识总量为a×2×2=4a,故A错误,
选项B:2012年底人类知识总量为a×2×2×2=8a,故B正确,
选项C:2022年底人类知识总量为8a×210=213a,故C正确,
选项D:2023年底人类知识总量为213a×25=218a,故D正确.
题16.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份0.8元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸________份.
【解析】设每天从报社买进x(250≤x≤400,x∈N)份报纸时,每月所获利润为y元,具体情况如下表.
项目 数量/份 单价/元 金额/元
买进 30x 2 60x
卖出 20x+10×250 3 60x+7 500
退回 10(x-250) 0.8 8x-2 000
则推销员每月所获得的利润y=[(60x+7 500)+(8x-2 000)]-60x=8x+5500(250≤x≤400,x∈N)
又由y=8x+5 500在[250,400]上单调递增,
所以当x=400时,y取得最大值8 700.
答案:400
题17.某制造商制造并出售圆柱形瓶装的某种饮料,瓶子的底面半径是r,高h=r(单位:cm),一个瓶子的制造成本是0.8πr2分,已知每出售1 mL(注:1 mL=1 cm3)的饮料,制造商可获利0.2分,且制造商能制造的瓶子底面的最大半径为6 cm.记每瓶饮料的利润为f(r),则f(3)=________,其实际意义是____________.
【解析】f(r)=0.2·πr2·r-0.8πr2=-0.8πr2(0<r≤6),
故f(3)=7.2 π-7.2 π=0.
表示当瓶子底面半径为3 cm时,利润为0.
答案:0 当瓶子底面半径为3 cm时,利润为0
题18.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=-48x+8 000,已知此生产线年产量最大为230吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本P(年总成本除以年产量)最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,且生产的产品全部售完,那么当年产量为多少吨时,年总利润可以获得最大?最大利润是多少?
【解析】(1)y=-48x+8 000,0<x≤230.
所以P==32,当且仅当x=200时取等号.
所以年产量为200吨时,生产每吨产品的平均成本P最低,最低成本为32万元.
(2)设利润为z万元,
则z=40x-y=40x-+48x-8 000
=-x2+88x-8 000=-(x-220)2+1 680,
即年产量为220吨时,利润最大为1 680万元.
题19.销售甲、乙两种商品所得利润分别是y1,y2万元,它们与投入资金x万元的关系分别为y1=m+a,y2=bx(其中m,a,b都为常数),函数y1,y2对应的曲线C1,C2如图所示.
(1)求函数y1与y2的解析式;
(2)若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值.
【解析】(1)由题意解得m=2,a=-2,故y1=2-2.
又由题意8b=4得b=,故y2=x.
(2)设销售甲商品投入资金x万元,利润为y万元,则乙投入(10-x)万元.
由(1)得y=2-2+=2-x+3,0≤x≤10.
令=t,则1≤t≤且x=t2-1,
故y=2t-+3=-t2+2t+=-(t-2)2+,1≤t≤,
当t=2即x=3时,y取最大值.
答:该商场所获利润的最大值为万元.
【综合突破拔高】
题20. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如表所示的关系.
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p元,则x,p分别为( )
A.35,225 B.40,300 C.45,350 D.45,400
【解析】选B.由表格可知,x与y满足一次函数关系,设y=ax+b(a≠0),把点(30,60)和点(40,30)代入得: 解得
所以y=-3x+150 (x≥30),所以销售利润p=y(x-30)=-3x2+240x-4 500(x≥30),所以当x=40时,p的值最大,最大值为300.
题21.某商场对顾客实行购物优惠活动,规定一次购物:
(1)如不超过200元,则不予优惠;
(2)如超过200元但不超过500元,则全款按9折优惠;
(3)如超过500元,其中500元按9折给予优惠,超过500的部分按8折给予优惠.
某人两次去购物,分别付款168元和423元,若他只去一次购买同样价格的商品,则应付款( )
A.472.8元 B.510.4元 C.522.8元 D.560.4元
【解析】选D.购物500元应付款500×0.9=450(元),
设第二次购物的原价为a,则200<a<500,故0.9a=423,解得a=470.
故两次购物原价为168+470=638(元).
若一次购物638元,则应付款500×0.9+138×0.8=560.4(元).
题22.已知样本中碳14的质量N随时间t(年)的衰变规律满足:N=N0·(N0表示碳14原来的质量),经过测定,良渚古城某文物样本中碳14的质量是原来的0.6倍,据此推测良渚古城遗址存在的时期距今大约是( )
(参考数据:log2 3≈1.6,log2 5≈2.3)
A.3440年 B.4010年
C.4580年 D.5160年
【解析】选B.由题意,可得0.6N0=N0·,
即=0.6=5 (3),两边取以2为底数的对数,
可得=log23-log25≈1.6-2.3=-0.7,
所以t≈0.7×5730=4011年.
题23. 8月到11月这四个月的某产品价格的市场平均价f(x)(单位:元/千克)与时间x(单位:月份)的数据如表
x 8 9 10 11
f(x) 28.00 33.99 36.00 34.02
现有三种函数模型:①f(x)=bx+a;②f(x)=ax2+bx+c;③f(x)=+a,找出你认为最适合的函数模型,并估计2020年12月份的该产品市场平均价( )
A.②,28元/千克
B.①,25元/千克
C.②,23元/千克
D.③,21元/千克
【解析】选A.因为f(x)的值随x的值先增后减,所以选f(x)=ax2+bx+c最合适.
第二组数据近似为(9,34),第四组近似为(11,34),得f(x)图象的对称轴为x=10,
故f(12)=f(8)=28.
题24.声强级L1(单位:dB)与声强I的函数关系式为:L1=10lg.若普通列车的声强级是95 dB,高速列车的声强级为45 dB,则普通列车的声强是高速列车声强的( )
A.106倍 B.105倍 C.104倍 D.103倍
【解析】选B.设普通列车的声强为I1,高速列车的声强为I2,
因为普通列车的声强级是95 dB,高速列车的声强级为45 dB,
所以95=10lg,45=10lg,
95=10lg=10,解得-2.5=lg I1,
所以I1=10-2.5,45=10lg =10,解得-7.5=lg I2,所以I2=10-7.5,
两式相除得=105,则普通列车的声强是高速列车声强的105倍.
题25(多选题). “双11”购物节中,某电商对顾客实行购物优惠活动,规定一次购物付款总额满一定额度,可以给予优惠:
(1)如果购物总额不超过50元,则不给予优惠;
(2)如果购物总额超过50元但不超过100元,可以使用一张5元优惠券;
(3)如果购物总额超过100元但不超过300元,则按标价给予9折优惠;
(4)如果购物总额超过300元,其中300元内的按第(3)条给予优惠,超过300元的部分给予8折优惠.
某人购买了部分商品,则下列说法正确的是 ( )
A.如果购物总额为78元,则应付款为73元 B.如果购物总额为228元,则应付款为205.2元
C.如果购物总额为368元,则应付款为294.4元
D.如果购物时一次性全部付款442.8元,则购物总额为516元
【解析】选ABD.如果购物总额为78元,满足超过50元但不超过100元,可以使用一张5元优惠券,则应付款为73元,故A正确;如果购物总额为228元,超过100元但不超过300元,则应付款为228×0.9=205.2元,故B正确;如果购物总额为368元,购物总额超过300元,则应付款为300×0.9+68×0.8=324.4元,故C错误;如果购物时一次性全部付款442.8元,说明购物总额超过300元,设购物总额为x元,则300×0.9+(x-300)×0.8=442.8,解得x=516元,故D正确.
题26(多选题).某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用y1(千元),乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示,则下列说法正确的是 ( )
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的总费用y1与证书数量x之间的函数关系式为y1=0.5x+1
C.若该单位需印制证书数量为8千个,则该单位选择甲厂更节省费用
D.当印制证书数量超过2千个时,乙厂的总费用y2与证书数量x之间的函数关系式为y2=x+
【解析】选ABD.对于选项A:由图可知甲厂制版费为1千元,印刷费平均每个为=0.5(元),所以选项A正确,对于选项B:设甲厂的总费用y1与证书数量x之间的函数关系式为y1=kx+b(k≠0),
则解得所以y1=0.5x+1,所以选项B正确,
对于选项C:由图象可知,当印制证书数量超过6千个时,乙厂费用少于甲厂费用,
所以若该单位需印制证书数量为8千个,则该单位选择乙厂更节省费用,所以选项C错误,
对于选项D:当印制证书数量超过2千个时,
设乙厂的总费用y2与证书数量x之间的函数关系式为y2=ax+c(a≠0),代入点(2,3)和点(6,4)得
解得所以y2=x+,所以选项D正确.
题27.某项研究表明:在考虑行车安全的情况下,某路段车流量F(单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v(假设车辆以相同速度v行驶,单位:米/秒)、平均车长l(单位:米)的值有关,其公式为F=.
(1)如果不限定车型,l=6.05,则最大车流量为________辆/小时;
(2)如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加______辆/小时.
【解析】(1)F=
因为=22,当v=11时分母取最小值,所以F=≤1 900,故最大车流量为:1 900辆/小时;
(2)F=,因为,所以F≤2 000,2 000-1 900=100(辆/小时),故最大车流量比(1)中的最大车流量增加100辆/小时.
答案:(1)1 900 (2)100
题28.某种细菌经30分钟数量变为原来的2倍,且该种细菌的繁殖规律为y=ekt,其中k为常数,t表示时间(单位:小时),y表示繁殖后细菌总个数,经过5小时,1个细菌通过繁殖个数变为________.
【解析】由题意知,当t=时,y=2,即2=,所以k=2ln 2,
所以y=.当t=5时,y==210=1 024.
即经过5小时,1个细菌通过繁殖个数变为1 024.
答案:1 024
题29.已知14C的半衰期为5 730年(是指经过5 730年后,14C的残余量占原始量的一半).设14C的原始量为a,经过x年后的残余量为b,残余量b与原始量a的关系如下:b=ae-kx,其中x表示经过的时间,k为一个常数.现测得湖南长沙马王堆汉墓女尸出土时14C的残余量约占原始量的76.7%.请你推断一下马王堆汉墓的大致年代为距今________年.(已知log20.767≈-0.4,ln 2≈0.69)
【解析】由题意可知,当x=5 730时ae-5 730k=a,解得k=.
现测得湖南长沙马王堆汉墓女尸出土时14C的残余量约占原始量的76.7%.
所以76.7%=,得ln 0.767=-x,
x=-5 730×=-5 730×log20.767≈2 292.
答案:2 292
题30.为节约能源,倡导绿色环保,某主题公园有60辆电动观光车供租赁使用,管理这些电动观光车的费用是每日120元.根据经验,若每辆电动观光车的日租金不超过5元,则电动观光车可以全部租出;若超过5元,则每超过1元,租不出去的电动观光车就增加2辆.为了便于结算,每辆电动观光车的日租金x(元)只取整数,并且要求出租电动观光车一日的收入必须高于这一日的管理费用,用y(元)表示出租电动观光车的日净收入(即一日出租电动观光车的总收入减去管理费用后的所得).
(1)求y关于x的解析式及其定义域;(2)当每辆电动观光车的日租金为多少元时,才能使一日的净收入最多?
【解析】(1)当x≤5时,y=60x-120,令60x-120>0,得x>2,因为x∈,所以3≤x≤5(x∈).
当x>5时,y=[60-2(x-5)]x-120=-2x2+70x-120,令-2x2+70x-120>0,即x2-35x+60<0,
上述不等式的整数解为2≤x≤33(x∈N*),所以5
(2)对于y=60x-120,3≤x≤5,x∈,显然当x=5时,ymax=180.
对于y=-2x2+70x-120=,5
题31. 小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为W(x)万元.在年产量不足万件时,(万元);在年产量不小于8万件时, (万元).每件产品售价为5元.通过市场分析,小王生产的商 品当年能全部售完.写出年利润L(x)(万元)关于年产量x(万件)的函数解析式.(注:年利润=年销售收入-固定成本-流动成本)
【解析】因为每件产品售价为5元,则x万件产品的销售收入为5x万元,依题意得:
当0
所以
题32.围建一个面积为360的矩形场地,要求矩形场地的一面利用30 m的旧墙(利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m).
分别写出矩形场地的另一边长C(单位:m)、旧墙维修费用P(单位:元)、新墙的造价R(单位:元)、建设矩形场地的总费用L(单位:元)关于利用旧墙的长度x(单位:m)的函数关系式.
【解析】矩形场地的另一边长C与利用的旧墙的长度x的关系式为.
旧墙的维修费用P与利用的旧墙的长度x的关系式为.
新墙的造价R与利用的旧墙的长度x的关系式为
总的建造费用L与利用的旧墙的长度x的关系式为
题33.运输一批海鲜,可在汽车、火车、飞机三种运输工具中选择,它们的速度分别为60千米/小时、120千米/小时,500千米/小时,每千米的运费分别为:20元、10元、50元.这批海鲜在运输过程中每小时的损耗为m元(m>0),运输的路程为s(千米).设用汽车、火车、飞机三种运输工具运输时各自的总费用(包括运费和损耗费)分别为y1(元),y2(元),y3(元).
(1)请分别写出y1,y2,y3的表达式;
(2)试确定使用哪种运输工具总费用最省.
【思路导引】(1)运输总费用=每千米的费用×.
(2)利用y1,y2,y3的表达式比较费用的大小.
【解析】(1).
(2)因为m>0,s>0,故20s>10s, ,
所以y1>y2恒成立,故只需比较y2与y3的大小关系即可,
令,
故当,即时,f(s)>0,
即y2
即y2>y3,此时选择飞机运输费用最省;
当,即时,f(s)=0,
即y2=y3,此时选择火车或飞机运输费用最省.
题34.据调查:人类在能源利用与森林砍伐中使CO2浓度增加.据测,2015年,2016年,2017年大气中的CO2浓度分别比2014年增加了1个单位,3个单位,6个单位.若用一个函数模拟每年CO2浓度增加的单位数y与年份增加数x的关系,模拟函数可选用二次函数f(x)=px2+qx+r(其中p,q,r为常数)或函数g(x)=a·bx+c(其中a,b,c为常数),又知2018年大气中的CO2浓度比2014年增加了16.5个单位,请问用以上哪个函数作模拟函数较好
【思路导引】首先根据已知条件确定两个模拟函数的解析式,再利用2018年的测量值检验模拟效果.
【解析】若以f(x)=px2+qx+r作模拟函数,
则依题意得:解得所以.
若以作模拟函数,
则解得所以.
利用f(x),g(x)对2018年CO2浓度作估算,则其数值分别为:
f(4)=10个单位,g(4)=10.5个单位,因为|f(4)-16.5|>|g(4)-16.5|,
所以作模拟函数与2018年的实际数据较为接近,故用作模拟函数较好.
- 0 -
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
