3.2代数式【素养基础达标】 2023—2024学年北师大版数学七年级上册(含解析)
文档属性
| 名称 | 3.2代数式【素养基础达标】 2023—2024学年北师大版数学七年级上册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-22 00:00:00 | ||
图片预览



文档简介
3.2代数式【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
一、整式的相关概念
1.代数式:代数式是由运算符号(加、减、乘、除、乘方、开方、绝对值)把数或表示数的字母连接而成的式子
2.代数式书写规范:
①数和字母相乘,可省略乘号,并把数字写在字母的前面;
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示. 一般情况下,按26个字母的顺序从左到右来写;
③后面带单位的相加或相减的式子要用括号括起来;
④除法运算写成分数形式,即除号改为分数线;
⑤带分数与字母相乘时,带分数要写成假分数的形式;
⑥当“1”与任何字母相乘时,“1”省略不写;当“-1”乘以字母时,只要在那个字母前加上“-”号.
1.单项式:由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
(1)单项式的系数是指单项式中的数字因数.
(2)单项式的次数是指单项式中所有字母的指数和.
2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
(1)在多项式中,不含字母的项叫做常数项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
3. 多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
(1)利用加法交换律重新排列时,各项应连同它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
4.整式:单项式和多项式统称为整式.
素养基础达标
一.选择题(共10小题)
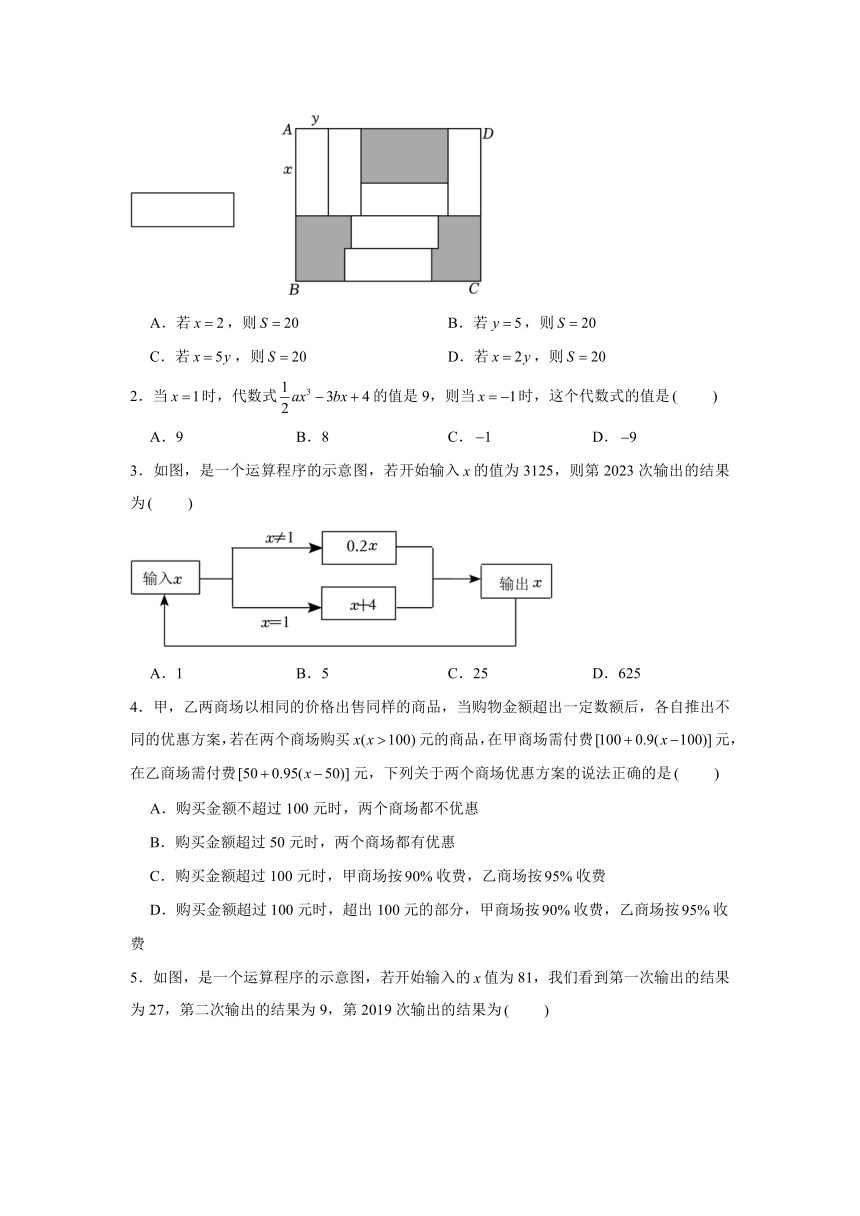
1.如图,在周长为60的长方形中放入六个相同的小长方形,若小长方形的面积为,长为,宽为,则
A.若,则 B.若,则
C.若,则 D.若,则
2.当时,代数式的值是9,则当时,这个代数式的值是
A.9 B.8 C. D.
3.如图,是一个运算程序的示意图,若开始输入的值为3125,则第2023次输出的结果为
A.1 B.5 C.25 D.625
4.甲,乙两商场以相同的价格出售同样的商品,当购物金额超出一定数额后,各自推出不同的优惠方案,若在两个商场购买元的商品,在甲商场需付费元,在乙商场需付费元,下列关于两个商场优惠方案的说法正确的是
A.购买金额不超过100元时,两个商场都不优惠
B.购买金额超过50元时,两个商场都有优惠
C.购买金额超过100元时,甲商场按收费,乙商场按收费
D.购买金额超过100元时,超出100元的部分,甲商场按收费,乙商场按收费
5.如图,是一个运算程序的示意图,若开始输入的值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,第2019次输出的结果为
A.27 B.9 C.1 D.3
6.如图所示的运算程序中,甲输入的为,乙输入的为,丙输入的为.若,则输出结果相同的是
A.甲和乙 B.甲和丙 C.乙和丙 D.三人均不相同
7.为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,其中甲种读本的价格为10元本,乙种读本的价格为8元本,若购买甲种读本本,则购买乙种读本的费用为
A.元 B.元 C.元 D.元
8.当时,代数式的值为4,则当时,代数式的值为
A.4 B. C.10 D.11
9.某电子产品进价为元,商店将价格提高作零售价销售,则该商品售价为
A.元 B.元 C.元 D.元
10.小丽跟几个同学去看电影,电影院准备了如下三种小食品餐供观众选择购买,若小丽和她的同学们一共买了10个汉堡,杯可乐,包薯片,则买餐的份数是
餐:一个汉堡 餐:一个汉堡一杯可乐 餐:一个汉堡一杯可乐一包薯片
A. B. C. D.
二.填空题(共8小题)
11.将方程变形为用含的式子表示,那么 .
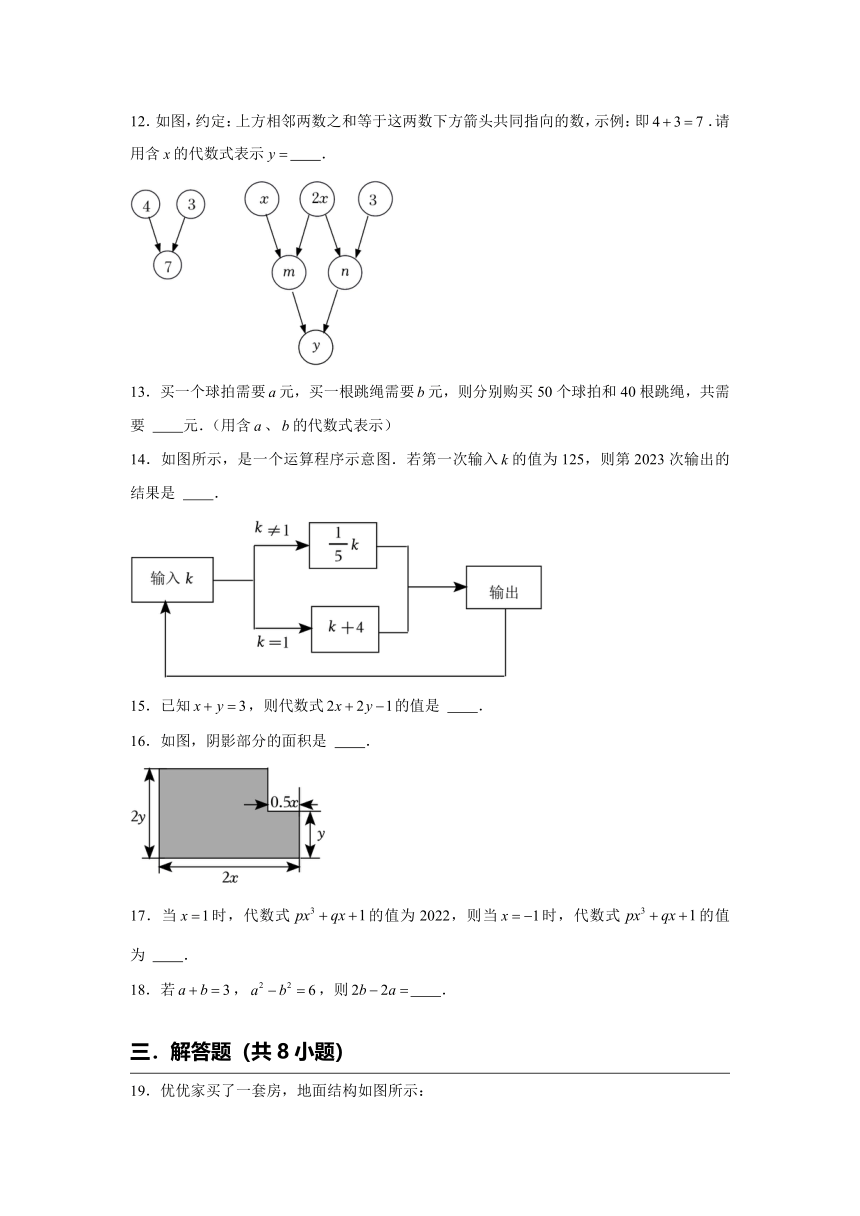
12.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数,示例:即.请用含的代数式表示 .
13.买一个球拍需要元,买一根跳绳需要元,则分别购买50个球拍和40根跳绳,共需要 元.(用含、的代数式表示)
14.如图所示,是一个运算程序示意图.若第一次输入的值为125,则第2023次输出的结果是 .
15.已知,则代数式的值是 .
16.如图,阴影部分的面积是 .
17.当时,代数式的值为2022,则当时,代数式的值为 .
18.若,,则 .
三.解答题(共8小题)
19.优优家买了一套房,地面结构如图所示:
根据图中的数据(单位:米)解答下列问题:
(1)用含、的式子表示地面的总面积;
(2)若,的倒数等于本身,若铺1平方米地砖的费用为80元,那么优优家铺地砖所用的总费用是多少元?
20.某游泳馆每年夏季推出两种游泳付费方式,方式一:不购买会员证,每次游泳付费9元;方式二:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元.设小明计划今年夏季游泳次数为为正整数).
(1)根据题意,将表格填写完整:
游泳次数 10 15
采用方式一付费(元 90 135
采用方式二付费(元 150
(2)通过计算说明,当和时,应选择哪种付费方式较合算?
(3)小明计划今年夏季游泳的费用为270元,问应选择哪种付费方式,使得游泳次数较多?
21.拖拉机油箱贮油60升,正常情况下,拖拉机工作1小时耗油5.5升,
(1)工作小时后油箱内还剩 升油;
(2)拖拉机工作多长时间后油箱内还剩38升油?(要求用方程解决问题)
22.爷爷与孙子下棋,爷爷赢1盘记1分,孙子赢1盘记3分,下了8盘,每盘都分出了胜负.
若爷爷赢了盘,请用含的代数式表示出孙子的得分数;
(2)若此时两人得分相同,请问爷爷赢了多少盘?
23.小王购买一套经济适用房,他准备在地面铺上地砖,地面结构如图所示.根据图中的数据(单位:,解答下列问题:
(1)用含、的代数式表示地面总面积;
(2)当,时,地面总面积为多少?若将地面全部铺上地砖,铺地砖的平均费用为80元,则铺地砖的总费用为多少元?
24.先阅读下面材料,再解决问题:在求多项式的值时,有时可以通过“降次”的方法,把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代入法”两种做法.例如:已知,求多项式的值.
方法一:,,原式.
方法二:,,原式.
(1)应用:已知,求多项式的值(只需用一种方法即可);
(2)拓展:已知,求多项式的值(只需用一种方法即可).
25.从一个边长为的正方形纸片(如图上剪去两个相同的小长方形,得到一个对数视力表中的“”的图案(如图,再将剪下的两个小长方形拼成一个新长方形(如图.
(1)用含有,的式子表示新长方形的长是 ,宽是 ;
(2)若空白缺口的宽度与相等,用含有的代数式表示黑色字母“”的周长.
(3)当时,求黑色字母“”的周长.
26.一天中午,小军到食堂排队买饭,看到、两个窗口排队的人数一样多(设为人,,就在窗口队伍后面,过了2分钟,他发现窗口每分钟有5人买好饭离开,窗口每分钟有8人买好饭离开,而且窗口队伍后面每分钟还增加4人.
(1)此时,若小军继续在窗口排队买饭,则他到达窗口所花的时间是多少?(用的代数式表示)
(2)此时,若小军迅速到窗口队伍后面重新排队,则他到达窗口所花的时间是多少?(用的代数式表示)
(3)此时,若他到达窗口所花的时间比继续留在窗口排队到达窗口多花的时间少,至少是多少?(不考虑其他因素)
3.2代数式【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
一、整式的相关概念
1.代数式:代数式是由运算符号(加、减、乘、除、乘方、开方、绝对值)把数或表示数的字母连接而成的式子
2.代数式书写规范:
①数和字母相乘,可省略乘号,并把数字写在字母的前面;
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示. 一般情况下,按26个字母的顺序从左到右来写;
③后面带单位的相加或相减的式子要用括号括起来;
④除法运算写成分数形式,即除号改为分数线;
⑤带分数与字母相乘时,带分数要写成假分数的形式;
⑥当“1”与任何字母相乘时,“1”省略不写;当“-1”乘以字母时,只要在那个字母前加上“-”号.
1.单项式:由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
(1)单项式的系数是指单项式中的数字因数.
(2)单项式的次数是指单项式中所有字母的指数和.
2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
(1)在多项式中,不含字母的项叫做常数项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
3. 多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
(1)利用加法交换律重新排列时,各项应连同它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
4.整式:单项式和多项式统称为整式.
素养基础达标
一.选择题(共10小题)
1.如图,在周长为60的长方形中放入六个相同的小长方形,若小长方形的面积为,长为,宽为,则
A.若,则 B.若,则
C.若,则 D.若,则
【答案】
【分析】由图可得,大长方形的长为,宽为,得大长方形的周长为,进而解决此题.
【解答】解:由图可得,大长方形的长为,宽为.
大长方形的周长为.
.
.当,则,此时,那么错误,故不符合题意.
.当,则,此时,那么错误,故不符合题意.
.当,则,,此时,那么正确,故符合题意.
.当,则,,此时,那么错误,故不符合题意.
故选:.
2.当时,代数式的值是9,则当时,这个代数式的值是
A.9 B.8 C. D.
【答案】
【分析】把代入代数式求出、的关系式,再把代入进行计算即可得解.
【解答】解:时,,
解得:,
当时,.
故选:.
3.如图,是一个运算程序的示意图,若开始输入的值为3125,则第2023次输出的结果为
A.1 B.5 C.25 D.625
【答案】
【分析】分别求出第一次输出的结果为625,第二次输出的结果为125,第三次输出的结果为25,第四次输出的结果为5,第五次输出的结果为1,第六次输出的结果为,由此得出规律,计算结果即可.
【解答】解:,
第一次输出的结果:,
第二次输出的结果:,
第三次输出的结果:,
第四次输出的结果:,
第五次输出的结果:,
第六次输出的结果:,
第七次输出的结果:,
第八次输出的结果:,
第九次输出的结果:,
由此得到规律,从第四次开始奇数次输出为1,偶数次输出为5,
第2023次输出结果为1.
故选:.
4.甲,乙两商场以相同的价格出售同样的商品,当购物金额超出一定数额后,各自推出不同的优惠方案,若在两个商场购买元的商品,在甲商场需付费元,在乙商场需付费元,下列关于两个商场优惠方案的说法正确的是
A.购买金额不超过100元时,两个商场都不优惠
B.购买金额超过50元时,两个商场都有优惠
C.购买金额超过100元时,甲商场按收费,乙商场按收费
D.购买金额超过100元时,超出100元的部分,甲商场按收费,乙商场按收费
【答案】
【分析】根据当时,在甲、乙两商场购物所付金额,可得出两商场给出的优惠方案,再对照四个选项,即可得出结论.
【解答】解:当时,在甲商场需付费元,
甲商场推出的优惠方案是:购买金额不超过100元时,不优惠,购买金额超过100元时,超出100元的部分按收费;
当时,在乙商场需付费元,
乙商场推出的优惠方案是:购买金额不超过50元时,不优惠,购买金额超过50元时,超出50元的部分按收费.
故选:.
5.如图,是一个运算程序的示意图,若开始输入的值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,第2019次输出的结果为
A.27 B.9 C.1 D.3
【答案】
【分析】根据如图的程序,分别求出前6次的输出结果各是多少,总结出规律,求出第2019次输出的结果为多少即可.
【解答】解:第1次输出的结果为27,
第2次输出的结果为9,
第3次输出的结果为:,
第4次输出的结果为:,
第5次输出的结果为:,
第6次输出的结果为:,
,
从第3次开始,输出的结果每2个数一个循环:3、1,
,
第2019次输出的结果为3.
故选:.
6.如图所示的运算程序中,甲输入的为,乙输入的为,丙输入的为.若,则输出结果相同的是
A.甲和乙 B.甲和丙 C.乙和丙 D.三人均不相同
【答案】
【分析】先判断,,,分别计算输出的结果得到答案.
【解答】解:
,,
甲输出的结果为:;
乙输出的结果为:;
丙输出的结果为:;
输出结果相同的是甲和丙,
故选:.
7.为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,其中甲种读本的价格为10元本,乙种读本的价格为8元本,若购买甲种读本本,则购买乙种读本的费用为
A.元 B.元 C.元 D.元
【答案】
【分析】直接利用乙的单价乙的本数乙的费用,进而得出答案.
【解答】解:设购买甲种读本本,则购买乙种读本的费用为:元.
故选:.
8.当时,代数式的值为4,则当时,代数式的值为
A.4 B. C.10 D.11
【答案】
【分析】将代入运算得到关于,的关系式的值,再将代入,整理后利用整体代入的方法解答即可.
【解答】解:当时,代数式的值为4,
,
.
当时,
代数式
.
故选:.
9.某电子产品进价为元,商店将价格提高作零售价销售,则该商品售价为
A.元 B.元 C.元 D.元
【答案】
【分析】此题的等量关系:进价提高率)售价列出代数式即可.
【解答】解:该商品售价为元.
故选:.
10.小丽跟几个同学去看电影,电影院准备了如下三种小食品餐供观众选择购买,若小丽和她的同学们一共买了10个汉堡,杯可乐,包薯片,则买餐的份数是
餐:一个汉堡 餐:一个汉堡一杯可乐 餐:一个汉堡一杯可乐一包薯片
A. B. C. D.
【答案】
【分析】根据点的饮料能确定在和餐中点了份汉堡,根据题意可得点餐的份数是.
【解答】解:杯可乐,
在和餐中点了份汉堡,
点餐的份数是.
故选:.
二.填空题(共8小题)
11.将方程变形为用含的式子表示,那么 .
【答案】.
【分析】把看作已知数求出即可.
【解答】解:,
,
,
.
故答案为:.
12.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数,示例:即.请用含的代数式表示 .
【答案】.
【分析】根据题意,可以用含的式子表示出即可.
【解答】解:由图可得,,
,
故答案为:.
13.买一个球拍需要元,买一根跳绳需要元,则分别购买50个球拍和40根跳绳,共需要 元.(用含、的代数式表示)
【答案】.
【分析】根据总钱数一个球拍的价格球拍的个数一根跳绳的价格跳绳的根数,即可列出共需的钱数.
【解答】解:分别购买50个球拍和40根跳绳,共需:(元,
故答案为:.
14.如图所示,是一个运算程序示意图.若第一次输入的值为125,则第2023次输出的结果是 1 .
【答案】1.
【分析】根据题中已知条件进行计算,找到输出数据的变化规律即可得到第2023次输出的结果了.
【解答】解:当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
由此可知,从第2次输出开始,输出结果是按“5、1”的顺序循环出现的,
,即输出的结果是1.
故答案为:1.
15.已知,则代数式的值是 5 .
【答案】5.
【分析】原式变形为,然后把整体代入计算即可.
【解答】解:,
当时,原式.
故答案为:5.
16.如图,阴影部分的面积是 .
【答案】.
【分析】根据图形可知,阴影部分的面积等于长为3,宽为的矩形的面积减去长为0.5,宽为的矩形的面积,然后列式计算即可.
【解答】解:由图可得,
阴影部分的面积是:,
故答案为:.
17.当时,代数式的值为2022,则当时,代数式的值为 .
【答案】.
【分析】当时,代数式的值为2022,可求出的值,从而可以解答.
【解答】解:当时,代数式的值为2022,
,
,
,
当时,
.
故答案为:.
18.若,,则 .
【答案】.
【分析】利用平方差公式变形等式,整体代入求出的值,再代入代数式求代数式的值.
【解答】解:,,
,即,
,
,
.
故答案为:.
三.解答题(共8小题)
19.优优家买了一套房,地面结构如图所示:
根据图中的数据(单位:米)解答下列问题:
(1)用含、的式子表示地面的总面积;
(2)若,的倒数等于本身,若铺1平方米地砖的费用为80元,那么优优家铺地砖所用的总费用是多少元?
【答案】(1)平方米;
(2)优优家铺地砖所用的总费用是3040元.
【分析】(1)先计算客厅的面积为平方米,卧室的面积为(平方米),厨房的面积为(平方米),卫生间的面积为平方米,把所有结果相加即可得出答案;
(2)由题意得,,把,代入(1)中的代数式,即可算出总面积,再用总面积乘以80即可得出答案.
【解答】解:(1)客厅的面积为平方米,
卧室的面积为(平方米),
厨房的面积为(平方米),
卫生间的面积为平方米,
地面的总面积是(平方米);
(2)由题意得:,,
(元.
优优家铺地砖所用的总费用是3040元.
20.某游泳馆每年夏季推出两种游泳付费方式,方式一:不购买会员证,每次游泳付费9元;方式二:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元.设小明计划今年夏季游泳次数为为正整数).
(1)根据题意,将表格填写完整:
游泳次数 10 15
采用方式一付费(元 90 135
采用方式二付费(元 150
(2)通过计算说明,当和时,应选择哪种付费方式较合算?
(3)小明计划今年夏季游泳的费用为270元,问应选择哪种付费方式,使得游泳次数较多?
【答案】(1),175,;
(2)当时,,故选择方式一更合算;
当时,,故选择方式二更合算;
(3)选择方式二他的游泳次数比较多.
【分析】(1)根据题意列式即可;
(2)把和分别代入即可得到结论;
(3)根据题意列方程即可得到结论.
【解答】解:(1)故答案为:,175,;
(2),
答:方式一比方式二的总费用多元;
当时,,故选择方式一更合算;
当时,,故选择方式二更合算;
(3)方式一:令,
解得:,
方式二:,
解得:,
,
选择方式二他的游泳次数比较多.
21.拖拉机油箱贮油60升,正常情况下,拖拉机工作1小时耗油5.5升,
(1)工作小时后油箱内还剩 升油;
(2)拖拉机工作多长时间后油箱内还剩38升油?(要求用方程解决问题)
【答案】(1);
(2)拖拉机工作4小时后油箱内还剩38升油.
【分析】(1)根据剩油量储油量工作小时的耗油量,列出算式即可;
(2)设工作时间为小时,根据还剩38升油列出方程求解即可.
【解答】解:(1)工作小时后油箱内还剩油升,
故答案为:;
(2)设工作时间为小时,根据题意得,
,
解得,
所以,拖拉机工作4小时后油箱内还剩38升油.
22.爷爷与孙子下棋,爷爷赢1盘记1分,孙子赢1盘记3分,下了8盘,每盘都分出了胜负.
若爷爷赢了盘,请用含的代数式表示出孙子的得分数;
(2)若此时两人得分相同,请问爷爷赢了多少盘?
【答案】(1);
(2)爷爷赢了6盘.
【分析】(1)由已知直接可得孙子的得分数为分;
(2)设爷爷赢了盘,根据两人得分相同列方程可解得答案.
【解答】解:(1)每盘都分出了胜负,爷爷赢了盘,
孙子赢了盘,
孙子赢1盘记,
孙子的得分数为分;
(2)设爷爷赢了盘,
根据题意得:
,
解得:,
答:爷爷赢了6盘.
23.小王购买一套经济适用房,他准备在地面铺上地砖,地面结构如图所示.根据图中的数据(单位:,解答下列问题:
(1)用含、的代数式表示地面总面积;
(2)当,时,地面总面积为多少?若将地面全部铺上地砖,铺地砖的平均费用为80元,则铺地砖的总费用为多少元?
【分析】(1)设客厅的宽是,卫生间的宽是,根据长方形的面积长宽,表示出总面积.
(2)根据第一问求得的代数式,将、的值代入即可求得总面积,从而可以求得总费用.
【解答】解:(1)设客厅的宽是,卫生间的宽是,
地面的总面积为:;
(2)当,时,地面的总面积为:,
铺地砖的平均费用为80元,
铺地砖的总费用为:(元.
24.先阅读下面材料,再解决问题:在求多项式的值时,有时可以通过“降次”的方法,把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代入法”两种做法.例如:已知,求多项式的值.
方法一:,,原式.
方法二:,,原式.
(1)应用:已知,求多项式的值(只需用一种方法即可);
(2)拓展:已知,求多项式的值(只需用一种方法即可).
【答案】(1),(2)5.
【分析】(1)用整体代入法进行计算;
(2)用逐步降次法进行计算.
【解答】解:(1),
,
原式
;
(2),
,
原式
.
25.从一个边长为的正方形纸片(如图上剪去两个相同的小长方形,得到一个对数视力表中的“”的图案(如图,再将剪下的两个小长方形拼成一个新长方形(如图.
(1)用含有,的式子表示新长方形的长是 ,宽是 ;
(2)若空白缺口的宽度与相等,用含有的代数式表示黑色字母“”的周长.
(3)当时,求黑色字母“”的周长.
【答案】(1),;(2);(3).
【分析】(1)利用图示数据解答即可;
(2)利用图示数据和周长的定义解答即可;
(3)将代入(2)中的代数式化简运算即可.
【解答】解:(1)新长方形的长是:,宽是:.
故答案为:,;
(2)空白缺口的宽度与相等,
.
.
黑色字母“”的周长为:
.
用含有的代数式表示黑色字母“”的周长为;
(3)当时,
黑色字母“”的周长为.
答:当时,黑色字母“”的周长为.
26.一天中午,小军到食堂排队买饭,看到、两个窗口排队的人数一样多(设为人,,就在窗口队伍后面,过了2分钟,他发现窗口每分钟有5人买好饭离开,窗口每分钟有8人买好饭离开,而且窗口队伍后面每分钟还增加4人.
(1)此时,若小军继续在窗口排队买饭,则他到达窗口所花的时间是多少?(用的代数式表示)
(2)此时,若小军迅速到窗口队伍后面重新排队,则他到达窗口所花的时间是多少?(用的代数式表示)
(3)此时,若他到达窗口所花的时间比继续留在窗口排队到达窗口多花的时间少,至少是多少?(不考虑其他因素)
【答案】(1);
(2);
(3)14.
【分析】(1)根据题意直接列式即可;
(2)根据题意直接列式即可;
(3)根据“到达窗口所花的时间比继续在窗口排队到达窗口所花的时间少”列不等式,求解即可.
【解答】解:(1)由题意得,他到达窗口所花的时间为:;
(2)由题意得,他到达窗口所花的时间为:;
(3)由题意得,,
解得,
为正整数,
至少是14.
2023-2024学年北师大版数学七年级上册
基础知识梳理
一、整式的相关概念
1.代数式:代数式是由运算符号(加、减、乘、除、乘方、开方、绝对值)把数或表示数的字母连接而成的式子
2.代数式书写规范:
①数和字母相乘,可省略乘号,并把数字写在字母的前面;
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示. 一般情况下,按26个字母的顺序从左到右来写;
③后面带单位的相加或相减的式子要用括号括起来;
④除法运算写成分数形式,即除号改为分数线;
⑤带分数与字母相乘时,带分数要写成假分数的形式;
⑥当“1”与任何字母相乘时,“1”省略不写;当“-1”乘以字母时,只要在那个字母前加上“-”号.
1.单项式:由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
(1)单项式的系数是指单项式中的数字因数.
(2)单项式的次数是指单项式中所有字母的指数和.
2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
(1)在多项式中,不含字母的项叫做常数项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
3. 多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
(1)利用加法交换律重新排列时,各项应连同它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
4.整式:单项式和多项式统称为整式.
素养基础达标
一.选择题(共10小题)
1.如图,在周长为60的长方形中放入六个相同的小长方形,若小长方形的面积为,长为,宽为,则
A.若,则 B.若,则
C.若,则 D.若,则
2.当时,代数式的值是9,则当时,这个代数式的值是
A.9 B.8 C. D.
3.如图,是一个运算程序的示意图,若开始输入的值为3125,则第2023次输出的结果为
A.1 B.5 C.25 D.625
4.甲,乙两商场以相同的价格出售同样的商品,当购物金额超出一定数额后,各自推出不同的优惠方案,若在两个商场购买元的商品,在甲商场需付费元,在乙商场需付费元,下列关于两个商场优惠方案的说法正确的是
A.购买金额不超过100元时,两个商场都不优惠
B.购买金额超过50元时,两个商场都有优惠
C.购买金额超过100元时,甲商场按收费,乙商场按收费
D.购买金额超过100元时,超出100元的部分,甲商场按收费,乙商场按收费
5.如图,是一个运算程序的示意图,若开始输入的值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,第2019次输出的结果为
A.27 B.9 C.1 D.3
6.如图所示的运算程序中,甲输入的为,乙输入的为,丙输入的为.若,则输出结果相同的是
A.甲和乙 B.甲和丙 C.乙和丙 D.三人均不相同
7.为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,其中甲种读本的价格为10元本,乙种读本的价格为8元本,若购买甲种读本本,则购买乙种读本的费用为
A.元 B.元 C.元 D.元
8.当时,代数式的值为4,则当时,代数式的值为
A.4 B. C.10 D.11
9.某电子产品进价为元,商店将价格提高作零售价销售,则该商品售价为
A.元 B.元 C.元 D.元
10.小丽跟几个同学去看电影,电影院准备了如下三种小食品餐供观众选择购买,若小丽和她的同学们一共买了10个汉堡,杯可乐,包薯片,则买餐的份数是
餐:一个汉堡 餐:一个汉堡一杯可乐 餐:一个汉堡一杯可乐一包薯片
A. B. C. D.
二.填空题(共8小题)
11.将方程变形为用含的式子表示,那么 .
12.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数,示例:即.请用含的代数式表示 .
13.买一个球拍需要元,买一根跳绳需要元,则分别购买50个球拍和40根跳绳,共需要 元.(用含、的代数式表示)
14.如图所示,是一个运算程序示意图.若第一次输入的值为125,则第2023次输出的结果是 .
15.已知,则代数式的值是 .
16.如图,阴影部分的面积是 .
17.当时,代数式的值为2022,则当时,代数式的值为 .
18.若,,则 .
三.解答题(共8小题)
19.优优家买了一套房,地面结构如图所示:
根据图中的数据(单位:米)解答下列问题:
(1)用含、的式子表示地面的总面积;
(2)若,的倒数等于本身,若铺1平方米地砖的费用为80元,那么优优家铺地砖所用的总费用是多少元?
20.某游泳馆每年夏季推出两种游泳付费方式,方式一:不购买会员证,每次游泳付费9元;方式二:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元.设小明计划今年夏季游泳次数为为正整数).
(1)根据题意,将表格填写完整:
游泳次数 10 15
采用方式一付费(元 90 135
采用方式二付费(元 150
(2)通过计算说明,当和时,应选择哪种付费方式较合算?
(3)小明计划今年夏季游泳的费用为270元,问应选择哪种付费方式,使得游泳次数较多?
21.拖拉机油箱贮油60升,正常情况下,拖拉机工作1小时耗油5.5升,
(1)工作小时后油箱内还剩 升油;
(2)拖拉机工作多长时间后油箱内还剩38升油?(要求用方程解决问题)
22.爷爷与孙子下棋,爷爷赢1盘记1分,孙子赢1盘记3分,下了8盘,每盘都分出了胜负.
若爷爷赢了盘,请用含的代数式表示出孙子的得分数;
(2)若此时两人得分相同,请问爷爷赢了多少盘?
23.小王购买一套经济适用房,他准备在地面铺上地砖,地面结构如图所示.根据图中的数据(单位:,解答下列问题:
(1)用含、的代数式表示地面总面积;
(2)当,时,地面总面积为多少?若将地面全部铺上地砖,铺地砖的平均费用为80元,则铺地砖的总费用为多少元?
24.先阅读下面材料,再解决问题:在求多项式的值时,有时可以通过“降次”的方法,把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代入法”两种做法.例如:已知,求多项式的值.
方法一:,,原式.
方法二:,,原式.
(1)应用:已知,求多项式的值(只需用一种方法即可);
(2)拓展:已知,求多项式的值(只需用一种方法即可).
25.从一个边长为的正方形纸片(如图上剪去两个相同的小长方形,得到一个对数视力表中的“”的图案(如图,再将剪下的两个小长方形拼成一个新长方形(如图.
(1)用含有,的式子表示新长方形的长是 ,宽是 ;
(2)若空白缺口的宽度与相等,用含有的代数式表示黑色字母“”的周长.
(3)当时,求黑色字母“”的周长.
26.一天中午,小军到食堂排队买饭,看到、两个窗口排队的人数一样多(设为人,,就在窗口队伍后面,过了2分钟,他发现窗口每分钟有5人买好饭离开,窗口每分钟有8人买好饭离开,而且窗口队伍后面每分钟还增加4人.
(1)此时,若小军继续在窗口排队买饭,则他到达窗口所花的时间是多少?(用的代数式表示)
(2)此时,若小军迅速到窗口队伍后面重新排队,则他到达窗口所花的时间是多少?(用的代数式表示)
(3)此时,若他到达窗口所花的时间比继续留在窗口排队到达窗口多花的时间少,至少是多少?(不考虑其他因素)
3.2代数式【素养基础达标】
2023-2024学年北师大版数学七年级上册
基础知识梳理
一、整式的相关概念
1.代数式:代数式是由运算符号(加、减、乘、除、乘方、开方、绝对值)把数或表示数的字母连接而成的式子
2.代数式书写规范:
①数和字母相乘,可省略乘号,并把数字写在字母的前面;
②字母和字母相乘,乘号可以省略不写或用“ · ” 表示. 一般情况下,按26个字母的顺序从左到右来写;
③后面带单位的相加或相减的式子要用括号括起来;
④除法运算写成分数形式,即除号改为分数线;
⑤带分数与字母相乘时,带分数要写成假分数的形式;
⑥当“1”与任何字母相乘时,“1”省略不写;当“-1”乘以字母时,只要在那个字母前加上“-”号.
1.单项式:由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.
(1)单项式的系数是指单项式中的数字因数.
(2)单项式的次数是指单项式中所有字母的指数和.
2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.
(1)在多项式中,不含字母的项叫做常数项.
(2)多项式中次数最高的项的次数,就是这个多项式的次数.
(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.
3. 多项式的降幂与升幂排列:
把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.
(1)利用加法交换律重新排列时,各项应连同它的符号一起移动位置;
(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.
4.整式:单项式和多项式统称为整式.
素养基础达标
一.选择题(共10小题)
1.如图,在周长为60的长方形中放入六个相同的小长方形,若小长方形的面积为,长为,宽为,则
A.若,则 B.若,则
C.若,则 D.若,则
【答案】
【分析】由图可得,大长方形的长为,宽为,得大长方形的周长为,进而解决此题.
【解答】解:由图可得,大长方形的长为,宽为.
大长方形的周长为.
.
.当,则,此时,那么错误,故不符合题意.
.当,则,此时,那么错误,故不符合题意.
.当,则,,此时,那么正确,故符合题意.
.当,则,,此时,那么错误,故不符合题意.
故选:.
2.当时,代数式的值是9,则当时,这个代数式的值是
A.9 B.8 C. D.
【答案】
【分析】把代入代数式求出、的关系式,再把代入进行计算即可得解.
【解答】解:时,,
解得:,
当时,.
故选:.
3.如图,是一个运算程序的示意图,若开始输入的值为3125,则第2023次输出的结果为
A.1 B.5 C.25 D.625
【答案】
【分析】分别求出第一次输出的结果为625,第二次输出的结果为125,第三次输出的结果为25,第四次输出的结果为5,第五次输出的结果为1,第六次输出的结果为,由此得出规律,计算结果即可.
【解答】解:,
第一次输出的结果:,
第二次输出的结果:,
第三次输出的结果:,
第四次输出的结果:,
第五次输出的结果:,
第六次输出的结果:,
第七次输出的结果:,
第八次输出的结果:,
第九次输出的结果:,
由此得到规律,从第四次开始奇数次输出为1,偶数次输出为5,
第2023次输出结果为1.
故选:.
4.甲,乙两商场以相同的价格出售同样的商品,当购物金额超出一定数额后,各自推出不同的优惠方案,若在两个商场购买元的商品,在甲商场需付费元,在乙商场需付费元,下列关于两个商场优惠方案的说法正确的是
A.购买金额不超过100元时,两个商场都不优惠
B.购买金额超过50元时,两个商场都有优惠
C.购买金额超过100元时,甲商场按收费,乙商场按收费
D.购买金额超过100元时,超出100元的部分,甲商场按收费,乙商场按收费
【答案】
【分析】根据当时,在甲、乙两商场购物所付金额,可得出两商场给出的优惠方案,再对照四个选项,即可得出结论.
【解答】解:当时,在甲商场需付费元,
甲商场推出的优惠方案是:购买金额不超过100元时,不优惠,购买金额超过100元时,超出100元的部分按收费;
当时,在乙商场需付费元,
乙商场推出的优惠方案是:购买金额不超过50元时,不优惠,购买金额超过50元时,超出50元的部分按收费.
故选:.
5.如图,是一个运算程序的示意图,若开始输入的值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,第2019次输出的结果为
A.27 B.9 C.1 D.3
【答案】
【分析】根据如图的程序,分别求出前6次的输出结果各是多少,总结出规律,求出第2019次输出的结果为多少即可.
【解答】解:第1次输出的结果为27,
第2次输出的结果为9,
第3次输出的结果为:,
第4次输出的结果为:,
第5次输出的结果为:,
第6次输出的结果为:,
,
从第3次开始,输出的结果每2个数一个循环:3、1,
,
第2019次输出的结果为3.
故选:.
6.如图所示的运算程序中,甲输入的为,乙输入的为,丙输入的为.若,则输出结果相同的是
A.甲和乙 B.甲和丙 C.乙和丙 D.三人均不相同
【答案】
【分析】先判断,,,分别计算输出的结果得到答案.
【解答】解:
,,
甲输出的结果为:;
乙输出的结果为:;
丙输出的结果为:;
输出结果相同的是甲和丙,
故选:.
7.为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,其中甲种读本的价格为10元本,乙种读本的价格为8元本,若购买甲种读本本,则购买乙种读本的费用为
A.元 B.元 C.元 D.元
【答案】
【分析】直接利用乙的单价乙的本数乙的费用,进而得出答案.
【解答】解:设购买甲种读本本,则购买乙种读本的费用为:元.
故选:.
8.当时,代数式的值为4,则当时,代数式的值为
A.4 B. C.10 D.11
【答案】
【分析】将代入运算得到关于,的关系式的值,再将代入,整理后利用整体代入的方法解答即可.
【解答】解:当时,代数式的值为4,
,
.
当时,
代数式
.
故选:.
9.某电子产品进价为元,商店将价格提高作零售价销售,则该商品售价为
A.元 B.元 C.元 D.元
【答案】
【分析】此题的等量关系:进价提高率)售价列出代数式即可.
【解答】解:该商品售价为元.
故选:.
10.小丽跟几个同学去看电影,电影院准备了如下三种小食品餐供观众选择购买,若小丽和她的同学们一共买了10个汉堡,杯可乐,包薯片,则买餐的份数是
餐:一个汉堡 餐:一个汉堡一杯可乐 餐:一个汉堡一杯可乐一包薯片
A. B. C. D.
【答案】
【分析】根据点的饮料能确定在和餐中点了份汉堡,根据题意可得点餐的份数是.
【解答】解:杯可乐,
在和餐中点了份汉堡,
点餐的份数是.
故选:.
二.填空题(共8小题)
11.将方程变形为用含的式子表示,那么 .
【答案】.
【分析】把看作已知数求出即可.
【解答】解:,
,
,
.
故答案为:.
12.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数,示例:即.请用含的代数式表示 .
【答案】.
【分析】根据题意,可以用含的式子表示出即可.
【解答】解:由图可得,,
,
故答案为:.
13.买一个球拍需要元,买一根跳绳需要元,则分别购买50个球拍和40根跳绳,共需要 元.(用含、的代数式表示)
【答案】.
【分析】根据总钱数一个球拍的价格球拍的个数一根跳绳的价格跳绳的根数,即可列出共需的钱数.
【解答】解:分别购买50个球拍和40根跳绳,共需:(元,
故答案为:.
14.如图所示,是一个运算程序示意图.若第一次输入的值为125,则第2023次输出的结果是 1 .
【答案】1.
【分析】根据题中已知条件进行计算,找到输出数据的变化规律即可得到第2023次输出的结果了.
【解答】解:当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
由此可知,从第2次输出开始,输出结果是按“5、1”的顺序循环出现的,
,即输出的结果是1.
故答案为:1.
15.已知,则代数式的值是 5 .
【答案】5.
【分析】原式变形为,然后把整体代入计算即可.
【解答】解:,
当时,原式.
故答案为:5.
16.如图,阴影部分的面积是 .
【答案】.
【分析】根据图形可知,阴影部分的面积等于长为3,宽为的矩形的面积减去长为0.5,宽为的矩形的面积,然后列式计算即可.
【解答】解:由图可得,
阴影部分的面积是:,
故答案为:.
17.当时,代数式的值为2022,则当时,代数式的值为 .
【答案】.
【分析】当时,代数式的值为2022,可求出的值,从而可以解答.
【解答】解:当时,代数式的值为2022,
,
,
,
当时,
.
故答案为:.
18.若,,则 .
【答案】.
【分析】利用平方差公式变形等式,整体代入求出的值,再代入代数式求代数式的值.
【解答】解:,,
,即,
,
,
.
故答案为:.
三.解答题(共8小题)
19.优优家买了一套房,地面结构如图所示:
根据图中的数据(单位:米)解答下列问题:
(1)用含、的式子表示地面的总面积;
(2)若,的倒数等于本身,若铺1平方米地砖的费用为80元,那么优优家铺地砖所用的总费用是多少元?
【答案】(1)平方米;
(2)优优家铺地砖所用的总费用是3040元.
【分析】(1)先计算客厅的面积为平方米,卧室的面积为(平方米),厨房的面积为(平方米),卫生间的面积为平方米,把所有结果相加即可得出答案;
(2)由题意得,,把,代入(1)中的代数式,即可算出总面积,再用总面积乘以80即可得出答案.
【解答】解:(1)客厅的面积为平方米,
卧室的面积为(平方米),
厨房的面积为(平方米),
卫生间的面积为平方米,
地面的总面积是(平方米);
(2)由题意得:,,
(元.
优优家铺地砖所用的总费用是3040元.
20.某游泳馆每年夏季推出两种游泳付费方式,方式一:不购买会员证,每次游泳付费9元;方式二:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元.设小明计划今年夏季游泳次数为为正整数).
(1)根据题意,将表格填写完整:
游泳次数 10 15
采用方式一付费(元 90 135
采用方式二付费(元 150
(2)通过计算说明,当和时,应选择哪种付费方式较合算?
(3)小明计划今年夏季游泳的费用为270元,问应选择哪种付费方式,使得游泳次数较多?
【答案】(1),175,;
(2)当时,,故选择方式一更合算;
当时,,故选择方式二更合算;
(3)选择方式二他的游泳次数比较多.
【分析】(1)根据题意列式即可;
(2)把和分别代入即可得到结论;
(3)根据题意列方程即可得到结论.
【解答】解:(1)故答案为:,175,;
(2),
答:方式一比方式二的总费用多元;
当时,,故选择方式一更合算;
当时,,故选择方式二更合算;
(3)方式一:令,
解得:,
方式二:,
解得:,
,
选择方式二他的游泳次数比较多.
21.拖拉机油箱贮油60升,正常情况下,拖拉机工作1小时耗油5.5升,
(1)工作小时后油箱内还剩 升油;
(2)拖拉机工作多长时间后油箱内还剩38升油?(要求用方程解决问题)
【答案】(1);
(2)拖拉机工作4小时后油箱内还剩38升油.
【分析】(1)根据剩油量储油量工作小时的耗油量,列出算式即可;
(2)设工作时间为小时,根据还剩38升油列出方程求解即可.
【解答】解:(1)工作小时后油箱内还剩油升,
故答案为:;
(2)设工作时间为小时,根据题意得,
,
解得,
所以,拖拉机工作4小时后油箱内还剩38升油.
22.爷爷与孙子下棋,爷爷赢1盘记1分,孙子赢1盘记3分,下了8盘,每盘都分出了胜负.
若爷爷赢了盘,请用含的代数式表示出孙子的得分数;
(2)若此时两人得分相同,请问爷爷赢了多少盘?
【答案】(1);
(2)爷爷赢了6盘.
【分析】(1)由已知直接可得孙子的得分数为分;
(2)设爷爷赢了盘,根据两人得分相同列方程可解得答案.
【解答】解:(1)每盘都分出了胜负,爷爷赢了盘,
孙子赢了盘,
孙子赢1盘记,
孙子的得分数为分;
(2)设爷爷赢了盘,
根据题意得:
,
解得:,
答:爷爷赢了6盘.
23.小王购买一套经济适用房,他准备在地面铺上地砖,地面结构如图所示.根据图中的数据(单位:,解答下列问题:
(1)用含、的代数式表示地面总面积;
(2)当,时,地面总面积为多少?若将地面全部铺上地砖,铺地砖的平均费用为80元,则铺地砖的总费用为多少元?
【分析】(1)设客厅的宽是,卫生间的宽是,根据长方形的面积长宽,表示出总面积.
(2)根据第一问求得的代数式,将、的值代入即可求得总面积,从而可以求得总费用.
【解答】解:(1)设客厅的宽是,卫生间的宽是,
地面的总面积为:;
(2)当,时,地面的总面积为:,
铺地砖的平均费用为80元,
铺地砖的总费用为:(元.
24.先阅读下面材料,再解决问题:在求多项式的值时,有时可以通过“降次”的方法,把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代入法”两种做法.例如:已知,求多项式的值.
方法一:,,原式.
方法二:,,原式.
(1)应用:已知,求多项式的值(只需用一种方法即可);
(2)拓展:已知,求多项式的值(只需用一种方法即可).
【答案】(1),(2)5.
【分析】(1)用整体代入法进行计算;
(2)用逐步降次法进行计算.
【解答】解:(1),
,
原式
;
(2),
,
原式
.
25.从一个边长为的正方形纸片(如图上剪去两个相同的小长方形,得到一个对数视力表中的“”的图案(如图,再将剪下的两个小长方形拼成一个新长方形(如图.
(1)用含有,的式子表示新长方形的长是 ,宽是 ;
(2)若空白缺口的宽度与相等,用含有的代数式表示黑色字母“”的周长.
(3)当时,求黑色字母“”的周长.
【答案】(1),;(2);(3).
【分析】(1)利用图示数据解答即可;
(2)利用图示数据和周长的定义解答即可;
(3)将代入(2)中的代数式化简运算即可.
【解答】解:(1)新长方形的长是:,宽是:.
故答案为:,;
(2)空白缺口的宽度与相等,
.
.
黑色字母“”的周长为:
.
用含有的代数式表示黑色字母“”的周长为;
(3)当时,
黑色字母“”的周长为.
答:当时,黑色字母“”的周长为.
26.一天中午,小军到食堂排队买饭,看到、两个窗口排队的人数一样多(设为人,,就在窗口队伍后面,过了2分钟,他发现窗口每分钟有5人买好饭离开,窗口每分钟有8人买好饭离开,而且窗口队伍后面每分钟还增加4人.
(1)此时,若小军继续在窗口排队买饭,则他到达窗口所花的时间是多少?(用的代数式表示)
(2)此时,若小军迅速到窗口队伍后面重新排队,则他到达窗口所花的时间是多少?(用的代数式表示)
(3)此时,若他到达窗口所花的时间比继续留在窗口排队到达窗口多花的时间少,至少是多少?(不考虑其他因素)
【答案】(1);
(2);
(3)14.
【分析】(1)根据题意直接列式即可;
(2)根据题意直接列式即可;
(3)根据“到达窗口所花的时间比继续在窗口排队到达窗口所花的时间少”列不等式,求解即可.
【解答】解:(1)由题意得,他到达窗口所花的时间为:;
(2)由题意得,他到达窗口所花的时间为:;
(3)由题意得,,
解得,
为正整数,
至少是14.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
