2023-2024学年人教版九年级数学上册21.3.2平均变化率问题与一元二次方程 课件(共12张PPT)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册21.3.2平均变化率问题与一元二次方程 课件(共12张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 985.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 11:01:17 | ||
图片预览





文档简介
(共12张PPT)
一元二次方程
解一元二次方程
一元二次方程
直接开平方法
配方法
实际问题与一元二次方程
公式法
因式分解法
一元二次方程的根与系数的关系
传播问题
几何图形
平均变化率
+
21.3 实际问题与一元二次方程
第2课时 平均变化率问题与一元二次方程
导入新课
思考 小明学习非常认真,学习成绩直线上升,第一次月考数学成绩是 75 分,第二次月考增长了 20%,第三次月考又增长了 20%,问他第三次数学成绩是多少?
如何解决这一问题呢?
第一次成绩
第二次成绩
第三次成绩
75分
增长20%
增长20%
75(1 + 20%)
75(1 + 20%)(1 + 20%)
90分
108分
合作探究
两年前生产 1 t 甲种药品的成本是 5000 元,生产 1 t 乙种药品的成本是 6000 元. 随着生产技术的进步,现在生产 1 t 甲种药品的成本是 3000 元,生产 1 t 乙种药品的成本是 3600 元. 哪种药品成本的年平均下降率较大?
问题 甲种、乙种药品年平均下降额分别是多少?
甲:(5000-3000)÷2=1000(元);
乙:(6000-3600)÷2=1200(元).
下降率 =
下降前的量 下降后的量
下降前的量
×100%
它们和下降率相同吗?
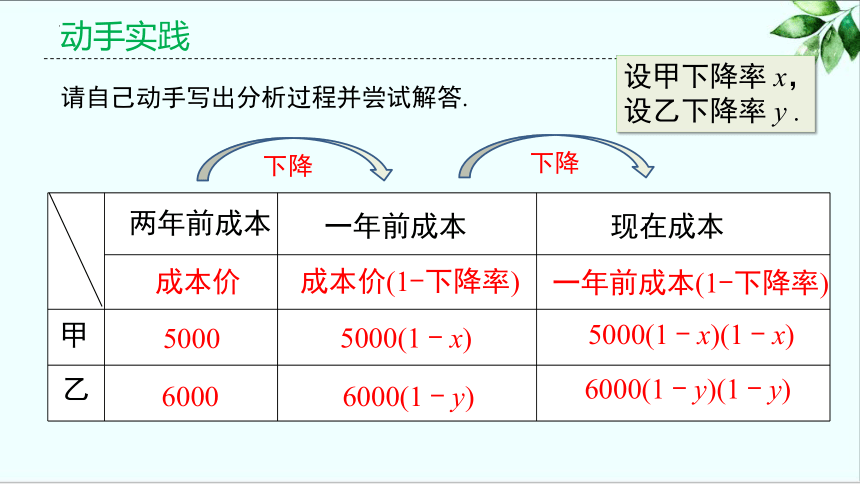
动手实践
请自己动手写出分析过程并尝试解答.
下降
下降
现在成本
一年前成本
两年前成本
成本价
成本价(1-下降率)
一年前成本(1-下降率)
甲
乙
5000
6000
设甲下降率 x,设乙下降率 y .
5000(1 - x)
6000(1 - y)
5000(1 - x)(1 - x)
6000(1 - y)(1 - y)
注意
一般下降率不可为负,且不大于 1.
解:设甲、乙种药品成本的年平均下降率为 x、y.
由题意得:
甲种药品:
5000(1 - x)2 = 3000
乙种药品:
6000(1 - y)2 = 3600
解方程,得
x1 ≈ 0.225,x2 ≈ 1.775(舍).
解方程,得
y1 ≈ 0.225, y2 ≈ 1.775(舍).
综上可知,甲、乙两种药品的下降率相同.
为什么呢?
经过计算,成本下降额较大的药品,它的成本下降率___________,应比较_________________.
不一定较大
降前及降后的价格
下降率是下降额与原成本的比值;
例题解析
某商店 4 月份的利润是 2500 元, 要使 6 月份的利润达到 3600 元,这两个月的平均增长率是多少?
四月份
五月份
六月份
2500
增长 x
增长 x
2500(1+ x)
2500(1+ x)(1+ x)
解:设平均增长率为 x.由题意得:
2500(1 + x)2 =3600
解得:x1= 0.2 ,x2= -2.2(不符合题意,舍).
答:平均每月增长率为 20%.
巩固练习
变式 1:某商店 4 月份的利润是 2500 元,要使第二季度的利润达到 9100 元,求这两个月的平均增长率是多少?
解:设平均增长率为 x.由题意得:
2500+2500(1+ x )2500(1 + x)2 =9100
解得:x1= 0.2 ,x2= -3.2(不符合题意,舍).
答:平均每月增长率为 20%.
即25 x2 +75 x +16=0
即(5 x -1)(5 x +16)=0
巩固练习
变式 2:某商店 4 月份的利润是 2500 元
“6 月的利润比 5 月的利润多 600 元”;求这两个月的平均增长率是多少?
解:设平均增长率为 x.由题意得:
2500(1+ x )+500 = 2500(1 + x)2
解得:x1= 0.2 ,x2= -1.2(不符合题意,舍).
答:平均每月增长率为 20%.
即25 x2 +25 x -6=0
即(5 x -1)(5 x +6)=0
巩固练习
变式 3:某商店 3 月份的利润是 2000 元,4 月份的利比 3 月份的利润增加 25%,要使 6 月份的利润达到 3600 元,求这 5、6 两个月的平 均增长率是多少?
四月份
五月份
六月份
2000(1+25%)
增长 x
增长 x
2000(1+25%)(1+ x)
2000(1+25%)(1+ x)(1+ x)
三月份
增长 25%
2000
解:设平均增长率为 x.由题意得:
即2500(1 + x)2 =3600
解得:x1= 0.2 ,x2= -2.2(不符合题意,舍).
答:平均每月增长率为 20%.
2000(1+25%)(1 + x)2 =3600
巩固练习
变式 4:某商店 6 月份的利润是 4 月份的利润的 1.44 倍,这 4、5 两个月的平均增长的百分率是多少
四月份
五月份
六月份
a
增长 x
增长 x
a(1+ x)
a(1+ x)(1+ x)
解:设平均增长率为 x.由题意得:
a(1 + x)2 =1.44a
解得:x1= 0.2 ,x2= -2.2(不符合题意,舍).
答:平均每月增长率为 20%.
总结
1.平均变化率:
平均增长(或降低)百分率为 x
增长(或降低) n 次前的量是 a
增长(或降低) n 次后的量是 b
2.年均增长率需要考虑实际情况取值.
一元二次方程
解一元二次方程
一元二次方程
直接开平方法
配方法
实际问题与一元二次方程
公式法
因式分解法
一元二次方程的根与系数的关系
传播问题
几何图形
平均变化率
+
21.3 实际问题与一元二次方程
第2课时 平均变化率问题与一元二次方程
导入新课
思考 小明学习非常认真,学习成绩直线上升,第一次月考数学成绩是 75 分,第二次月考增长了 20%,第三次月考又增长了 20%,问他第三次数学成绩是多少?
如何解决这一问题呢?
第一次成绩
第二次成绩
第三次成绩
75分
增长20%
增长20%
75(1 + 20%)
75(1 + 20%)(1 + 20%)
90分
108分
合作探究
两年前生产 1 t 甲种药品的成本是 5000 元,生产 1 t 乙种药品的成本是 6000 元. 随着生产技术的进步,现在生产 1 t 甲种药品的成本是 3000 元,生产 1 t 乙种药品的成本是 3600 元. 哪种药品成本的年平均下降率较大?
问题 甲种、乙种药品年平均下降额分别是多少?
甲:(5000-3000)÷2=1000(元);
乙:(6000-3600)÷2=1200(元).
下降率 =
下降前的量 下降后的量
下降前的量
×100%
它们和下降率相同吗?
动手实践
请自己动手写出分析过程并尝试解答.
下降
下降
现在成本
一年前成本
两年前成本
成本价
成本价(1-下降率)
一年前成本(1-下降率)
甲
乙
5000
6000
设甲下降率 x,设乙下降率 y .
5000(1 - x)
6000(1 - y)
5000(1 - x)(1 - x)
6000(1 - y)(1 - y)
注意
一般下降率不可为负,且不大于 1.
解:设甲、乙种药品成本的年平均下降率为 x、y.
由题意得:
甲种药品:
5000(1 - x)2 = 3000
乙种药品:
6000(1 - y)2 = 3600
解方程,得
x1 ≈ 0.225,x2 ≈ 1.775(舍).
解方程,得
y1 ≈ 0.225, y2 ≈ 1.775(舍).
综上可知,甲、乙两种药品的下降率相同.
为什么呢?
经过计算,成本下降额较大的药品,它的成本下降率___________,应比较_________________.
不一定较大
降前及降后的价格
下降率是下降额与原成本的比值;
例题解析
某商店 4 月份的利润是 2500 元, 要使 6 月份的利润达到 3600 元,这两个月的平均增长率是多少?
四月份
五月份
六月份
2500
增长 x
增长 x
2500(1+ x)
2500(1+ x)(1+ x)
解:设平均增长率为 x.由题意得:
2500(1 + x)2 =3600
解得:x1= 0.2 ,x2= -2.2(不符合题意,舍).
答:平均每月增长率为 20%.
巩固练习
变式 1:某商店 4 月份的利润是 2500 元,要使第二季度的利润达到 9100 元,求这两个月的平均增长率是多少?
解:设平均增长率为 x.由题意得:
2500+2500(1+ x )2500(1 + x)2 =9100
解得:x1= 0.2 ,x2= -3.2(不符合题意,舍).
答:平均每月增长率为 20%.
即25 x2 +75 x +16=0
即(5 x -1)(5 x +16)=0
巩固练习
变式 2:某商店 4 月份的利润是 2500 元
“6 月的利润比 5 月的利润多 600 元”;求这两个月的平均增长率是多少?
解:设平均增长率为 x.由题意得:
2500(1+ x )+500 = 2500(1 + x)2
解得:x1= 0.2 ,x2= -1.2(不符合题意,舍).
答:平均每月增长率为 20%.
即25 x2 +25 x -6=0
即(5 x -1)(5 x +6)=0
巩固练习
变式 3:某商店 3 月份的利润是 2000 元,4 月份的利比 3 月份的利润增加 25%,要使 6 月份的利润达到 3600 元,求这 5、6 两个月的平 均增长率是多少?
四月份
五月份
六月份
2000(1+25%)
增长 x
增长 x
2000(1+25%)(1+ x)
2000(1+25%)(1+ x)(1+ x)
三月份
增长 25%
2000
解:设平均增长率为 x.由题意得:
即2500(1 + x)2 =3600
解得:x1= 0.2 ,x2= -2.2(不符合题意,舍).
答:平均每月增长率为 20%.
2000(1+25%)(1 + x)2 =3600
巩固练习
变式 4:某商店 6 月份的利润是 4 月份的利润的 1.44 倍,这 4、5 两个月的平均增长的百分率是多少
四月份
五月份
六月份
a
增长 x
增长 x
a(1+ x)
a(1+ x)(1+ x)
解:设平均增长率为 x.由题意得:
a(1 + x)2 =1.44a
解得:x1= 0.2 ,x2= -2.2(不符合题意,舍).
答:平均每月增长率为 20%.
总结
1.平均变化率:
平均增长(或降低)百分率为 x
增长(或降低) n 次前的量是 a
增长(或降低) n 次后的量是 b
2.年均增长率需要考虑实际情况取值.
同课章节目录
