专题4 追及与相遇问题-2024年高考物理一轮复习专题讲义(教案)
文档属性
| 名称 | 专题4 追及与相遇问题-2024年高考物理一轮复习专题讲义(教案) |  | |
| 格式 | docx | ||
| 文件大小 | 468.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-23 08:23:33 | ||
图片预览




文档简介
追及与相遇问题
考点一 速度大追速度小
1.分析思路: 可概括为“一个临界条件”“两个等量关系”。
一个临界条件:速度大者追速度小者:二者速度相等是判断能否追上的临界条件,若此时追不上,二者距离最小。
两个等量关系: 时间等量关系和位移等量关系,通过画草图找出两物体的时间关系和位移关系是解题的突破口。
2.常见情况解析:
典型示例 图像 说明
匀减速追匀速 开始追时,两物体间距离为x0,之后两物体间的距离在减小,当两物体速度相等时,即t=t0时刻: ①若Δx=x0,则恰能追上,两物体只能相遇一次,这也是避免相撞的临界条件; ②若Δxx0,则相遇两次,设t1时刻Δx1=x0,两物体第一次相遇,则t2时刻两物体第二次相遇(t2-t0=t0-t1)
匀速追匀加速
匀减速追匀加速
题型一 匀减速追匀加速
在水平轨道上有两列火车A和B,相距x,A车在后面做初速度为v0、加速度大小为2a的匀减速直线运动,而B车同时做初速度为零、加速度大小为a的匀加速直线运动,两车运动方向相同。要使两车不相撞,求A车的初速度v0满足什么条件?
v0≤
两车不相撞的临界条件:A车追上B车时其速度与B车相等。设A、B两车从相距x到A车追上B车时,A车的位移为xA、末速度为vA、所用时间为t′,B车的位移为xB、末速度为vB,运动过程如图甲所示。现用三种方法解答如下:
法一 情境分析法
对A车有xA=v0t′+(-2a)×t′2,vA=v0+(-2a)×t′
对B车有xB=at′2,vB=at′
两车位移关系有x=xA-xB
追上时,两车不相撞的临界条件是vA=vB
联立以上各式解得v0=
故要使两车不相撞,A车的初速度v0应满足的条件是v0≤。
法二 函数判断法
利用判别式求解,由题意可知xA=x+xB,即v0t′+×(-2a)×t′2=x+at′2
整理得3at′2-2v0t′+2x=0
这是一个关于时间t′的一元二次方程,当根的判别式Δ=(-2v0)2-4·3a·2x=0时,两车刚好不相撞,
解得v0=,所以要使两车不相撞,A车的初速度v0应满足的条件是v0≤。
法三 图像分析法
利用v-t图像求解,作A、B两车的v -t图像,如图乙所示,设经过t′时间两车刚好不相撞,则对A车有vA=v′=v0-2at′
对B车有vB=v′=at′
以上两式联立解得t′=
经t′时间两车发生的位移之差为原来两车间距离x,它可用图中的阴影面积表示,由图像可知
x=v0·t′=v0·=,
解得v0=,
所以要使两车不相撞,A车的初速度v0应满足的条件是v0≤。
题型二 利用v-t图像分析追及相遇问题
(多选)甲、乙两车在平直公路上同向行驶,其v-t图像如图所示.已知两车在t=3 s时并排行驶,则( )
A.在t=1 s时,甲车在乙车后
B.在t=0时,甲车在乙车前方7.5 m处
C.两车另一次并排行驶的时刻是t=2 s
D.甲、乙车两次并排行驶的位置之间沿公路方向的距离为40 m
BD
t=3 s时,甲、乙两车并排行驶,此时v甲=30 m/s,v乙=25 m/s,由v-t图线与时间轴所围“面积”表示位移知,0~3 s内甲车位移x甲=×3×30 m=45 m,乙车位移x乙=×3×(10+25) m=52.5 m,故t=0时,甲、乙两车相距Δx1=x乙-x甲=7.5 m,即甲车在乙车前方7.5 m处,选项B正确;0~1 s内,x甲′=×1×10 m=5 m,x乙′=×1×(10+15) m=12.5 m,Δx2=x乙′-x甲′=7.5 m=Δx1,说明在t=1 s时甲、乙两车第一次并排行驶,选项A、C错误;甲、乙两车两次并排行驶的位置之间的距离为x=x甲-x甲′=45 m-5 m=40 m,选项D正确.
追及相遇问题常用以下三种方法:
(1)情境分析法
分析物体运动过程→画运动示意图→找位移关系→列位移方程
(2)图像分析法
①若为x-t图像,图像相交即代表两物体相遇。
②若为v-t图像,利用图像与坐标轴围成的面积进行分析。
③若为a-t图像,可转化为v-t图像进行分析。
(3) 函数判断法
根据位移关系,写出关于t的一元二次方程,其中根的判别式。
当时,方程有两个不相等的实数根,即相遇两次;
当时,方程有两个相等的实数根,即只有一个解,相遇一次;
当时,方程无实数根,即无解,不能相遇。
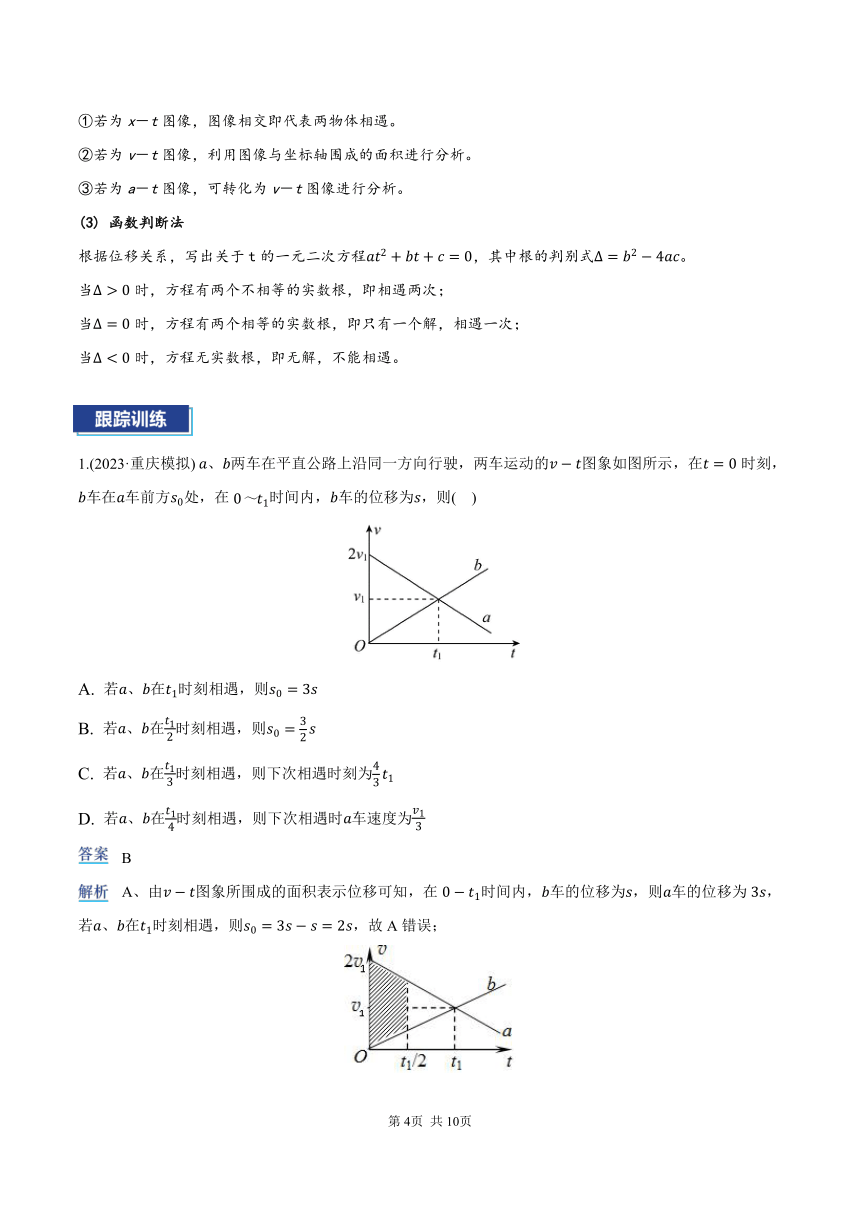
1.(2023·重庆模拟)、两车在平直公路上沿同一方向行驶,两车运动的图象如图所示,在时刻,车在车前方处,在时间内,车的位移为,则( )
A. 若、在时刻相遇,则
B. 若、在时刻相遇,则
C. 若、在时刻相遇,则下次相遇时刻为
D. 若、在时刻相遇,则下次相遇时车速度为
B
A、由图象所围成的面积表示位移可知,在时间内,车的位移为,则车的位移为,若、在时刻相遇,则,故A错误;
B、若、在时刻相遇,由图象可知,阴影部分对应的面积等于,即,而已知在时间内,车的位移为,则可得,故B正确。
C、若、在时刻相遇,根据对称性知,下次相遇时刻为,故C错误。
D、若、在时刻相遇,根据对称性知,下次相遇时刻为,根据几何关系知下次相遇时车速度为,故D错误。
故选:。
2.(2023·江西赣州市高三模拟)在赣州市南河大桥扩建工程中,双向桥梁已完成了某一通车方向的建设,为保持双向车辆正常通行,临时将其改成双向车道.如图所示,引桥与桥面对接处,有两车道合并一车道的对接口,A、B两车相距s0=4 m时,B车正以vB=4 m/s速度匀速行驶,A车正以vA=7 m/s的速度借道超越同向行驶的B车,此时A车司机发现前方距离车头s=16 m处的并道对接口,A、B两车长度均为L=4 m,且不考虑A车变道过程的影响.
(1)若A车司机放弃超车,且立即驶入与B车相同的行驶车道,A车至少以多大的加速度刹车匀减速,才能避免与B车相撞.
(2)若A车司机加速超车,A车的最大加速度为a=3 m/s2,请通过计算分析A车能否实现安全超车.
(1) m/s2 (2)见解析
(1)A车减速到与B车同速时,若恰未与B车相碰,则A车将不会与B车相碰,设经历的时间为t,则A车位移xA=t ①
B车位移xB=vBt ②
xA-xB=s0 ③
由①②③式联立解得t= s
则A车与B车不相碰,刹车时的最小加速度
amin== m/s2= m/s2.
(2)设A车加速t′时间后车尾到达B车车头,则s0+2L=vAt′+at′2-vBt′,解得t′=2 s
在此时间内,A车向前运动了xA1=vAt′+at′2
计算可得xA1=20 m>s=16 m,说明在离并道对接口16 m的距离上以3 m/s2的加速度加速不能实现安全超车.
考点二 速度小追速度大
速度小者追速度大者:二者速度相等是判断能否追上的临界条件,若此时追不上,二者距离最大。
常见情况解析:
典型示例 图像 说明
匀加速追匀速 ①0~t0时段,后面物体与前面物体间距离不断增大; ②t=t0时,两物体相距最远,为x0+Δx(x0为两物体初始距离); ③t>t0时,后面物体追及前面物体的过程中,两物体间距离不断减小; ④能追上且只能相遇一次
匀速追匀减速
匀加速追匀减速
题型一 匀加速追匀速
一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以a=3 m/s2的加速度开始加速行驶,恰在这时一辆自行车以6 m/s的速度匀速驶过,从后边超过汽车.则汽车从路口启动后,在追上自行车之前经过多长时间两车相距最远?此时两车的距离是多少?
2 s 6 m
法一 分析法:汽车与自行车的速度相等时相距最远,设此时经过的时间为t,两车间的距离为Δx,则有v=at
所以t==2 s,Δx=vt-at2=6 m.
法二 二次函数法:设汽车在追上自行车之前经过时间t两车相距最远,则Δx=vt-at2
代入已知数据得Δx=6t-t2
由二次函数求极值的条件知:t=2 s时,Δx有最大值为6 m
所以t=2 s时两车相距最远,为6 m.
法三 图像法:自行车和汽车的v-t图像如图所示,由图可以看出,在相遇前,t1时刻两车速度相等,两车相距最远,此时的距离为阴影三角形的面积,v1=6 m/s
所以有t1== s=2 s,
Δx== m=6 m.
题型二 匀速运动追赶匀减速运动
汽车A以vA=4 m/s的速度向右做匀速直线运动,发现前方相距x0=7 m处、以vB=10 m/s的速度同向运动的汽车B正开始匀减速刹车直到静止后保持不动,其刹车的加速度大小a=2 m/s2。从此刻开始计时。求:
(1)A追上B前,A、B间的最远距离是多少。
(2)经过多长时间A恰好追上B。
(1)16 m (2)8 s
(1)当A、B两汽车速度相等时,两车间的距离最远,即v=vB-at=vA,解得t=3 s
此时汽车A的位移xA=vAt=12 m
汽车B的位移xB=vBt-at2=21 m
故最远距离Δxmax=xB-xA+x0=16 m。
(2)汽车B从开始减速直到静止经历的时间t1= =5 s,
运动的位移xB′==25 m
汽车A在t1时间内运动的位移xA′=vAt1=20 m
此时相距Δx=xB′-xA′+x0=12 m
汽车A需再运动的时间t2==3 s
故A追上B所用时间t总=t1+t2=8 s。
求解追及、相遇问题时的2点技巧
“临界条件”分析:题目中的关键字眼,如“刚好”“恰好”“最多”“至少”等即为临界条件。
“实际情况”分析:(易错点)若被追赶的物体做匀减速运动,一定要注意被追上前该物体是否已经停止运动。
1.如图所示,在某次车模比赛中,可看成质点的甲、乙两汽车模型在同一直线上运动,相距s=8 m,车模甲以v甲=5 m/s的速度向右匀速运动,已关闭电源的车模乙此时的速度v乙=12 m/s,向右做匀减速运动,加速度a=-2 m/s2,那么车模甲追上车模乙所用的时间为( )
A.s B.8 s C.8.8 s D.s
C
车模乙速度减为0的时间t1==s=6 s,此时车模乙的位移x乙== m=36 m,车模甲的位移x甲=v甲t1=5×6 m=30 m,由于x甲2.(2021·甘肃兰州一中高三月考)A、B两车在同一直线上向右匀速运动,B车在A车前,A车的速度大小为v1=8 m/s,B车的速度大小为v2=20 m/s,如图所示。当A、B两车相距x0=28 m时,B车因前方突发情况紧急刹车(刹车过程可视为匀减速直线运动),加速度大小为a=2 m/s2,从此时开始计时,求:
(1)A车追上B车之前,两者相距的最大距离;
(2)A车追上B车所用的时间;
(3)从安全行驶的角度考虑,为避免两车相撞,题设条件下,在B车刹车的同时,A车刹车的最小加速度。
(1)64 m (2)16 s (3)0.25 m/s2
(1)当A、B两车速度相等时,相距最远,根据速度关系得v1=v2-at1
代入数据解得t1=6 s
此时,根据位移时间的关系得xA1=v1t1
xB1=v2t1-at
Δxm=xB1+x0-xA1
代入数据解得Δxm=64 m。
(2)B车刹车到停止运动所用时间
t0==10 s
发生的位移xB2==100 m
此时xA2=v1t0=80 m
则xA2<x0+xB2,
可见此时A车并未追上B车,而是在B车停止后才追上B车,停止后A车运动时间为
t2==6 s
故所用总时间为t=t0+t2=16 s。
(3)A车刹车减速至0时刚好追上B车,加速度最小
代入数据解得aA=0.25 m/s2。
第10页 共10页
考点一 速度大追速度小
1.分析思路: 可概括为“一个临界条件”“两个等量关系”。
一个临界条件:速度大者追速度小者:二者速度相等是判断能否追上的临界条件,若此时追不上,二者距离最小。
两个等量关系: 时间等量关系和位移等量关系,通过画草图找出两物体的时间关系和位移关系是解题的突破口。
2.常见情况解析:
典型示例 图像 说明
匀减速追匀速 开始追时,两物体间距离为x0,之后两物体间的距离在减小,当两物体速度相等时,即t=t0时刻: ①若Δx=x0,则恰能追上,两物体只能相遇一次,这也是避免相撞的临界条件; ②若Δx
匀速追匀加速
匀减速追匀加速
题型一 匀减速追匀加速
在水平轨道上有两列火车A和B,相距x,A车在后面做初速度为v0、加速度大小为2a的匀减速直线运动,而B车同时做初速度为零、加速度大小为a的匀加速直线运动,两车运动方向相同。要使两车不相撞,求A车的初速度v0满足什么条件?
v0≤
两车不相撞的临界条件:A车追上B车时其速度与B车相等。设A、B两车从相距x到A车追上B车时,A车的位移为xA、末速度为vA、所用时间为t′,B车的位移为xB、末速度为vB,运动过程如图甲所示。现用三种方法解答如下:
法一 情境分析法
对A车有xA=v0t′+(-2a)×t′2,vA=v0+(-2a)×t′
对B车有xB=at′2,vB=at′
两车位移关系有x=xA-xB
追上时,两车不相撞的临界条件是vA=vB
联立以上各式解得v0=
故要使两车不相撞,A车的初速度v0应满足的条件是v0≤。
法二 函数判断法
利用判别式求解,由题意可知xA=x+xB,即v0t′+×(-2a)×t′2=x+at′2
整理得3at′2-2v0t′+2x=0
这是一个关于时间t′的一元二次方程,当根的判别式Δ=(-2v0)2-4·3a·2x=0时,两车刚好不相撞,
解得v0=,所以要使两车不相撞,A车的初速度v0应满足的条件是v0≤。
法三 图像分析法
利用v-t图像求解,作A、B两车的v -t图像,如图乙所示,设经过t′时间两车刚好不相撞,则对A车有vA=v′=v0-2at′
对B车有vB=v′=at′
以上两式联立解得t′=
经t′时间两车发生的位移之差为原来两车间距离x,它可用图中的阴影面积表示,由图像可知
x=v0·t′=v0·=,
解得v0=,
所以要使两车不相撞,A车的初速度v0应满足的条件是v0≤。
题型二 利用v-t图像分析追及相遇问题
(多选)甲、乙两车在平直公路上同向行驶,其v-t图像如图所示.已知两车在t=3 s时并排行驶,则( )
A.在t=1 s时,甲车在乙车后
B.在t=0时,甲车在乙车前方7.5 m处
C.两车另一次并排行驶的时刻是t=2 s
D.甲、乙车两次并排行驶的位置之间沿公路方向的距离为40 m
BD
t=3 s时,甲、乙两车并排行驶,此时v甲=30 m/s,v乙=25 m/s,由v-t图线与时间轴所围“面积”表示位移知,0~3 s内甲车位移x甲=×3×30 m=45 m,乙车位移x乙=×3×(10+25) m=52.5 m,故t=0时,甲、乙两车相距Δx1=x乙-x甲=7.5 m,即甲车在乙车前方7.5 m处,选项B正确;0~1 s内,x甲′=×1×10 m=5 m,x乙′=×1×(10+15) m=12.5 m,Δx2=x乙′-x甲′=7.5 m=Δx1,说明在t=1 s时甲、乙两车第一次并排行驶,选项A、C错误;甲、乙两车两次并排行驶的位置之间的距离为x=x甲-x甲′=45 m-5 m=40 m,选项D正确.
追及相遇问题常用以下三种方法:
(1)情境分析法
分析物体运动过程→画运动示意图→找位移关系→列位移方程
(2)图像分析法
①若为x-t图像,图像相交即代表两物体相遇。
②若为v-t图像,利用图像与坐标轴围成的面积进行分析。
③若为a-t图像,可转化为v-t图像进行分析。
(3) 函数判断法
根据位移关系,写出关于t的一元二次方程,其中根的判别式。
当时,方程有两个不相等的实数根,即相遇两次;
当时,方程有两个相等的实数根,即只有一个解,相遇一次;
当时,方程无实数根,即无解,不能相遇。
1.(2023·重庆模拟)、两车在平直公路上沿同一方向行驶,两车运动的图象如图所示,在时刻,车在车前方处,在时间内,车的位移为,则( )
A. 若、在时刻相遇,则
B. 若、在时刻相遇,则
C. 若、在时刻相遇,则下次相遇时刻为
D. 若、在时刻相遇,则下次相遇时车速度为
B
A、由图象所围成的面积表示位移可知,在时间内,车的位移为,则车的位移为,若、在时刻相遇,则,故A错误;
B、若、在时刻相遇,由图象可知,阴影部分对应的面积等于,即,而已知在时间内,车的位移为,则可得,故B正确。
C、若、在时刻相遇,根据对称性知,下次相遇时刻为,故C错误。
D、若、在时刻相遇,根据对称性知,下次相遇时刻为,根据几何关系知下次相遇时车速度为,故D错误。
故选:。
2.(2023·江西赣州市高三模拟)在赣州市南河大桥扩建工程中,双向桥梁已完成了某一通车方向的建设,为保持双向车辆正常通行,临时将其改成双向车道.如图所示,引桥与桥面对接处,有两车道合并一车道的对接口,A、B两车相距s0=4 m时,B车正以vB=4 m/s速度匀速行驶,A车正以vA=7 m/s的速度借道超越同向行驶的B车,此时A车司机发现前方距离车头s=16 m处的并道对接口,A、B两车长度均为L=4 m,且不考虑A车变道过程的影响.
(1)若A车司机放弃超车,且立即驶入与B车相同的行驶车道,A车至少以多大的加速度刹车匀减速,才能避免与B车相撞.
(2)若A车司机加速超车,A车的最大加速度为a=3 m/s2,请通过计算分析A车能否实现安全超车.
(1) m/s2 (2)见解析
(1)A车减速到与B车同速时,若恰未与B车相碰,则A车将不会与B车相碰,设经历的时间为t,则A车位移xA=t ①
B车位移xB=vBt ②
xA-xB=s0 ③
由①②③式联立解得t= s
则A车与B车不相碰,刹车时的最小加速度
amin== m/s2= m/s2.
(2)设A车加速t′时间后车尾到达B车车头,则s0+2L=vAt′+at′2-vBt′,解得t′=2 s
在此时间内,A车向前运动了xA1=vAt′+at′2
计算可得xA1=20 m>s=16 m,说明在离并道对接口16 m的距离上以3 m/s2的加速度加速不能实现安全超车.
考点二 速度小追速度大
速度小者追速度大者:二者速度相等是判断能否追上的临界条件,若此时追不上,二者距离最大。
常见情况解析:
典型示例 图像 说明
匀加速追匀速 ①0~t0时段,后面物体与前面物体间距离不断增大; ②t=t0时,两物体相距最远,为x0+Δx(x0为两物体初始距离); ③t>t0时,后面物体追及前面物体的过程中,两物体间距离不断减小; ④能追上且只能相遇一次
匀速追匀减速
匀加速追匀减速
题型一 匀加速追匀速
一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以a=3 m/s2的加速度开始加速行驶,恰在这时一辆自行车以6 m/s的速度匀速驶过,从后边超过汽车.则汽车从路口启动后,在追上自行车之前经过多长时间两车相距最远?此时两车的距离是多少?
2 s 6 m
法一 分析法:汽车与自行车的速度相等时相距最远,设此时经过的时间为t,两车间的距离为Δx,则有v=at
所以t==2 s,Δx=vt-at2=6 m.
法二 二次函数法:设汽车在追上自行车之前经过时间t两车相距最远,则Δx=vt-at2
代入已知数据得Δx=6t-t2
由二次函数求极值的条件知:t=2 s时,Δx有最大值为6 m
所以t=2 s时两车相距最远,为6 m.
法三 图像法:自行车和汽车的v-t图像如图所示,由图可以看出,在相遇前,t1时刻两车速度相等,两车相距最远,此时的距离为阴影三角形的面积,v1=6 m/s
所以有t1== s=2 s,
Δx== m=6 m.
题型二 匀速运动追赶匀减速运动
汽车A以vA=4 m/s的速度向右做匀速直线运动,发现前方相距x0=7 m处、以vB=10 m/s的速度同向运动的汽车B正开始匀减速刹车直到静止后保持不动,其刹车的加速度大小a=2 m/s2。从此刻开始计时。求:
(1)A追上B前,A、B间的最远距离是多少。
(2)经过多长时间A恰好追上B。
(1)16 m (2)8 s
(1)当A、B两汽车速度相等时,两车间的距离最远,即v=vB-at=vA,解得t=3 s
此时汽车A的位移xA=vAt=12 m
汽车B的位移xB=vBt-at2=21 m
故最远距离Δxmax=xB-xA+x0=16 m。
(2)汽车B从开始减速直到静止经历的时间t1= =5 s,
运动的位移xB′==25 m
汽车A在t1时间内运动的位移xA′=vAt1=20 m
此时相距Δx=xB′-xA′+x0=12 m
汽车A需再运动的时间t2==3 s
故A追上B所用时间t总=t1+t2=8 s。
求解追及、相遇问题时的2点技巧
“临界条件”分析:题目中的关键字眼,如“刚好”“恰好”“最多”“至少”等即为临界条件。
“实际情况”分析:(易错点)若被追赶的物体做匀减速运动,一定要注意被追上前该物体是否已经停止运动。
1.如图所示,在某次车模比赛中,可看成质点的甲、乙两汽车模型在同一直线上运动,相距s=8 m,车模甲以v甲=5 m/s的速度向右匀速运动,已关闭电源的车模乙此时的速度v乙=12 m/s,向右做匀减速运动,加速度a=-2 m/s2,那么车模甲追上车模乙所用的时间为( )
A.s B.8 s C.8.8 s D.s
C
车模乙速度减为0的时间t1==s=6 s,此时车模乙的位移x乙== m=36 m,车模甲的位移x甲=v甲t1=5×6 m=30 m,由于x甲
(1)A车追上B车之前,两者相距的最大距离;
(2)A车追上B车所用的时间;
(3)从安全行驶的角度考虑,为避免两车相撞,题设条件下,在B车刹车的同时,A车刹车的最小加速度。
(1)64 m (2)16 s (3)0.25 m/s2
(1)当A、B两车速度相等时,相距最远,根据速度关系得v1=v2-at1
代入数据解得t1=6 s
此时,根据位移时间的关系得xA1=v1t1
xB1=v2t1-at
Δxm=xB1+x0-xA1
代入数据解得Δxm=64 m。
(2)B车刹车到停止运动所用时间
t0==10 s
发生的位移xB2==100 m
此时xA2=v1t0=80 m
则xA2<x0+xB2,
可见此时A车并未追上B车,而是在B车停止后才追上B车,停止后A车运动时间为
t2==6 s
故所用总时间为t=t0+t2=16 s。
(3)A车刹车减速至0时刚好追上B车,加速度最小
代入数据解得aA=0.25 m/s2。
第10页 共10页
同课章节目录
