专题一 匀变速直线运动的规律及应用-2024年高考物理一轮复习专题讲义(教案)
文档属性
| 名称 | 专题一 匀变速直线运动的规律及应用-2024年高考物理一轮复习专题讲义(教案) | 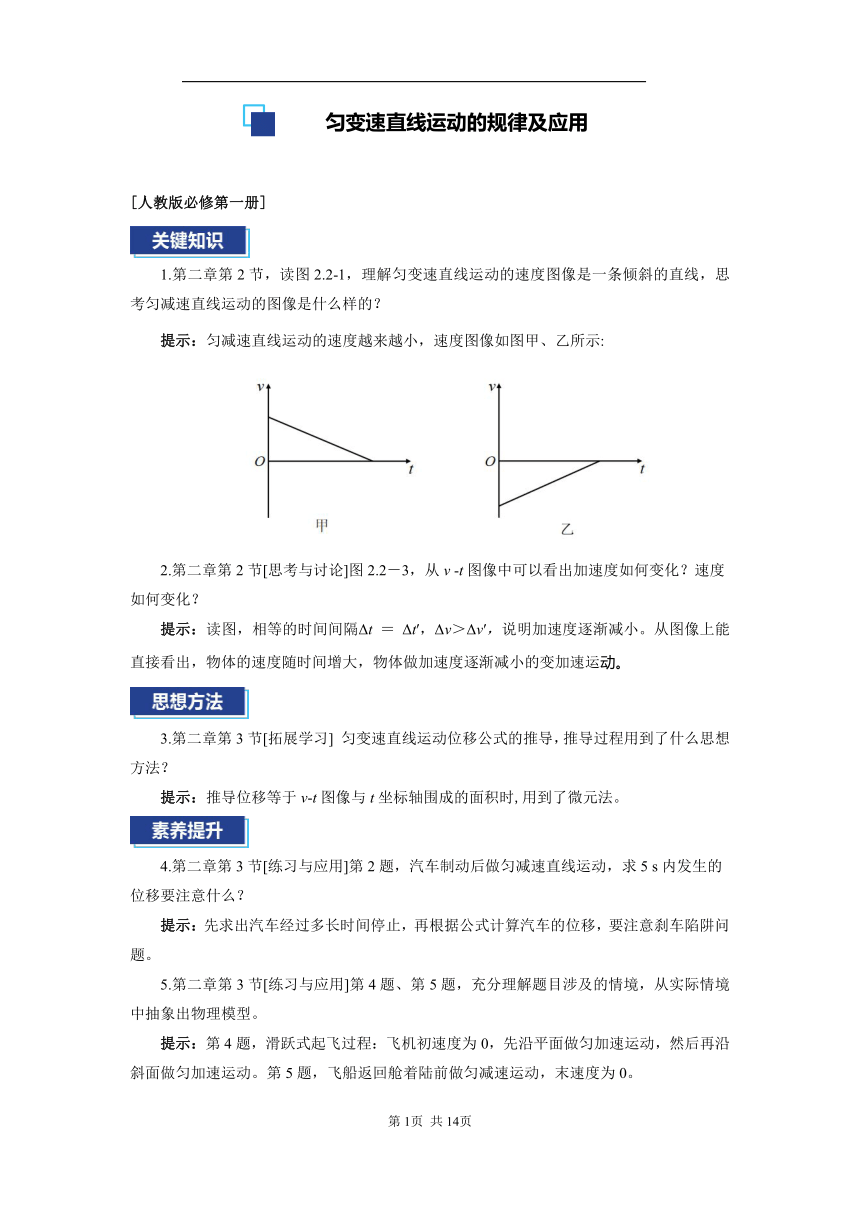 | |
| 格式 | docx | ||
| 文件大小 | 598.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-23 08:34:50 | ||
图片预览





文档简介
匀变速直线运动的规律及应用
[人教版必修第一册]
1.第二章第2节,读图2.2-1,理解匀变速直线运动的速度图像是一条倾斜的直线,思考匀减速直线运动的图像是什么样的?
提示:匀减速直线运动的速度越来越小,速度图像如图甲、乙所示:
2.第二章第2节[思考与讨论]图2.2-3,从v t图像中可以看出加速度如何变化?速度如何变化?
提示:读图,相等的时间间隔Δt = Δt′,Δv>Δv′,说明加速度逐渐减小。从图像上能直接看出,物体的速度随时间增大,物体做加速度逐渐减小的变加速运动。
3.第二章第3节[拓展学习] 匀变速直线运动位移公式的推导,推导过程用到了什么思想方法?
提示:推导位移等于v t图像与t坐标轴围成的面积时,用到了微元法。
4.第二章第3节[练习与应用]第2题,汽车制动后做匀减速直线运动,求5 s内发生的位移要注意什么?
提示:先求出汽车经过多长时间停止,再根据公式计算汽车的位移,要注意刹车陷阱问题。
5.第二章第3节[练习与应用]第4题、第5题,充分理解题目涉及的情境,从实际情境中抽象出物理模型。
提示:第4题,滑跃式起飞过程:飞机初速度为0,先沿平面做匀加速运动,然后再沿斜面做匀加速运动。第5题,飞船返回舱着陆前做匀减速运动,末速度为0。
考点一 匀变速直线运动的基本规律及应用
1.匀变速直线运动的定义和分类
(1)匀变速直线运动:沿着一条直线,且 加速度 不变的运动。
(2)当a与v0 同向 时,物体做匀加速直线运动;
当a与v0 反向 时,物体做匀减速直线运动;
匀变速运动的v-t图线是一条倾斜的直线,如图所示,图线①(斜向上)为匀加速直线运动;图线②(斜向下)为匀减速直线运动。
2.三个基本公式
(1)速度与时间的关系: ;
(2)位移与时间的关系: ;
(3)速度与位移的关系 : ;
应用三个基本公式解决问题时,分析题目条件中有哪些已知量,v 0、v、a、t、x知道任意3个,可选择合适的公式求出另外2个。
题型一 基本公式和速度位移关系式的应用
如图所示,甲从A地沿平直公路由静止匀加速跑向B地,当甲前进距离为s1时,乙从距A地s2处的C点由静止出发,加速度与甲相同,最后两人同时到达B地,则A、B两地距离为( )
A. B. C. D.
B
设甲前进距离为s1时,速度为v,甲、乙匀加速直线运动的加速度为a,乙出发到达B点的时间为t,则有:vt+at2 at2=s2 s1,根据速度位移公式得,解得;则AB的距离
故选B。
题型二 刹车问题
(2022·苏州市模拟)汽车以20 m/s 的速度在平直公路上行驶,遇到紧急情况急刹车时的加速度大小为5 m/s2,则自驾驶员急踩刹车开始,经过2s与5s汽车的位移之比为( )
A.5∶4 B.4∶5 C.3∶4 D.4∶3
C
汽车速度减为零的时间t0==s=4s,刹车2s内的位移x1=v0t+at2=20×2 m-×5×22 m=30 m,由于刹车时间为4s,刹车5s内的位移等于刹车4s内的位移x2==40 m,所以经过2s与5s汽车的位移之比为3∶4,故选项C正确。
题型三 先减速后反向加速
(多选)在足够长的光滑固定斜面上,有一物体以10 m/s的初速度沿斜面向上运动,物体的加速度大小始终为5 m/s2、方向沿斜面向下,当物体的位移大小为7.5 m时,下列说法正确的是( )
A.物体运动时间可能为1s B.物体运动时间可能为3s
C.物体运动时间可能为(2+) s D.物体此时的速度大小一定为5 m/s
ABC
以沿斜面向上为正方向,则a=-5 m/s2,当物体的位移为沿斜面向上7.5 m时,x=7.5m,由运动学公式x=v0t+at2,解得t1=3 s或t2=1 s,故A、B正确.当物体的位移为沿斜面向下7.5 m时,x=-7.5 m,由x=v0t+at2,解得t3=(2+) s或t4=(2-) s(舍去),故C正确.由速度时间公式v=v0+at,解得v1=-5 m/s、v2=5 m/s、v3=-5 m/s,故D错误.
1.v0、v、a、x均为矢量,正、负号表示矢量的方向。匀变速直线运动中,通常以初速度v0的方向为正方向;当v0=0时,一般以加速度a的方向为正方向。速度、加速度、位移的方向与正方向相同时取正,相反时取负。
2.充分理解刹车问题的实际情况:①驾驶员看到前方有情况到操作刹车的时间(反应时间)车做匀速运动。②当车速减小到0以后,车会停下来,需要根据刹车时间(从开始刹车到速度减小到0的时间),判断汽车实际行驶的距离。
3.对加速度不变、先减速后反向加速的问题,求解时可分过程列式,也可对全过程列式,但必须注意x、v、a等矢量的正负号及物理意义。
1.(2023·湖南长沙市第一中学月考)如图所示,一质点做匀加速直线运动先后经过A、B、C三点,已知从A到B和从B到C速度的增加量Δv均为6 m/s,AB间的距离x1=3 m,BC间的距离x2=13 m,则该质点的加速度为( )
A.3.6 m/s2 B.4 m/s2
C.4.2 m/s2 D.4.8 m/s2
A
因为从A到B和从B到C速度的增加量Δv均为6 m/s,可知从A到B的时间和从B到C的时间相等,有Δv=aT=6 m/s,Δx=x2-x1=aT2=10 m,联立可得T= s,a=3.6 m/s2,A正确.
2.一汽车刹车做匀减速直线运动,在第二秒内的位移为3 m,第三秒内的位移为0.125 m,则汽车的加速度大小为( )
A.3 m/s2 B.3.5 m/s2
C.4 m/s2 D.4.25 m/s2
C
假设汽车第3s内已停止运动,由匀变速直线运动的推论可知,1.5s时的速度为
则2s末的速度为
第3s内的位移可表示为
联立代入数据解得
,
则第2s内的位移为
即假设符合题意。
故选C。
3.如图所示,一个小球以初速度10 m/s从斜面底端O冲上一固定斜面,A、B、C依次是斜面上的三个点,AC间距为8 m,B为AC中点。经过2 s,小球第一次通过A点,又经4 s第二次通过C点,不计一切摩擦,则下列说法正确的是( )
A.质点的加速度大小为3 m/s2
B.OA间距为8 m
C.第一次通过B点的速度大小一定为2 m/s
D.第3 s末经过B点
C
根据匀变速直线运动规律,设OA间距为x,知通过OA所用时间t=2 s,有x=v0t-at2,质点又经4s第二次通过C点,有x+8=v0(t+4)-a(t+4)2,联立可得a=2 m/s2,x=16 m,故A、B错误;B点为AC的中间位置,OB间距为x1=x+4 m=20 m,由-=-2ax1得vB=2 m/s,故C正确;第3s末小球的位移为:大于OB间距20 m,所以第3 s末小球已经越过了B点,故D错误。
考点二 匀变速直线运动的重要推论及应用
1.两个重要推论
(1)物体在一段时间内的平均速度等于这段时间 中间时刻 的瞬时速度,还等于初、末时刻速度矢量和的 一半 ,即:。(补充:中间位移的瞬时速度公式:)
(2)任意两个连续相等的时间间隔T内的位移之差为一恒量,即:Δx=x2-x1=x3-x2=…=xn-xn-1= aT2。可以推广得到xm-xn=(m-n)aT2。
2.初速度为零的匀变速直线运动的五个推论
(1)1T末、2T末、3T末……nT末瞬时速度的比为v1∶v2∶v3∶…∶vn=1∶2∶3∶…∶n 。
(2)1T内、2T内、3T内……nT内位移的比为x1∶x2∶x3∶…∶xn= 12∶22∶32∶…∶n2 。
(3)第一个T内、第二个T内、第三个T内……第n个T内位移的比为x1′∶x2′∶x3′∶…∶xn′= 1∶3∶5∶…∶(2n-1) 。
(4)从静止开始运动位移x、2x、3x……nx所用时间的比为t1∶t2∶t3∶…∶tn= 。
(5)从静止开始通过连续相等的位移所用时间的比为t1′∶t2′∶t3′∶…∶tn′=。
题型一 平均速度公式
一物体做匀加速直线运动,通过一段位移Δx所用的时间为t1,紧接着通过下一段位移Δx所用时间为t2。则物体运动的加速度为( )
A. B. C. D.
A
物体做匀加速直线运动在前一段所用的时间为,平均速度为,即为时刻的瞬时速度;
物体在后一段所用的时间为,平均速度为 ,即为时刻的瞬时速度。
速度由变化到的时间为
所以加速度为
故选A。
题型二 位移差公式
(2023·重庆市实验外国语学校高三检测)物体从静止开始做匀加速直线运动,已知第4 s内与第2 s内的位移之差是8 m,则下列说法错误的是( )
A.物体运动的加速度为4 m/s2
B.第2 s内的位移为6 m
C.第2 s末的速度为2 m/s
D.物体在0~5 s内的平均速度为10 m/s
C
根据位移差公式得x4-x2=2aT2,可知a== m/s2=4 m/s2,故A正确,不符合题意;第2 s内的位移为x2-x1=at22-at12=×4×(22-12) m=6 m,故B正确,不符合题意;第2 s末的速度为v=at2=4×2 m/s=8 m/s,故C错误,符合题意;物体在0~5 s内的平均速度=== m/s=10 m/s,故D正确,不符合题意.
题型三 初速度为零的匀变速直线运动比例式
(多选)如图所示,一冰壶以速度v垂直进入三个完全相同的矩形区域做匀减速直线运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是( )
A.v1∶v2∶v3=3∶2∶1
B.v1∶v2∶v3=∶∶1
C.t1∶t2∶t3=1∶∶
D.t1∶t2∶t3=(-)∶(-1)∶1
BD
冰壶做匀减速直线运动且末速度为零,可以将它的运动看成反向的初速度为零的匀加速直线运动。初速度为零的匀加速直线运动中通过连续三段相等位移的时间之比为1∶(-1)∶(-),故t1∶t2∶t3=(-)∶(-1)∶1,选项C错误,D正确;由v2-v02=2ax可得,初速度为零的匀加速直线运动中通过连续相等位移的速度之比为1∶∶,故v1∶v2∶v3=∶∶1,选项A错误,B正确。
题型四 车辆进出站问题
ETC是电子不停车收费系统的简称,汽车分别通过ETC通道和人工收费通道的流程如图所示。假设汽车以v1=12 m/s的速度朝收费站沿直线行驶,如果过ETC通道,需要在距收费站中心线前d=10 m处正好匀减速至v2=4 m/s,匀速通过中心线后,再匀加速至v1正常行驶;如果过人工收费通道,需要恰好在中心线处匀减速至零,经过t0=20 s缴费成功后,再启动汽车匀加速至v1正常行驶,设汽车加速和减速过程中的加速度大小均为1 m/s2。
求:
(1)汽车过ETC通道时,从开始减速到恢复正常行驶过程中的位移大小;
(2)汽车过人工收费通道时,应在离收费站中心线多远处开始减速;
(3)汽车过ETC通道比过人工收费通道节约的时间。
(1)138 m (2)72 m (3)25 s
(1)过ETC通道时,减速的位移和加速的位移相等,则x1==64 m
故总的位移x总1=2x1+d=138 m。
(2)过人工收费通道时,开始减速时距离中心线为
x2==72 m。
(3)过ETC通道的时间
t1=×2+ =18.5 s
过人工收费通道的时间
t2=×2+t0=44 s
x总2=2x2=144 m
二者的位移差Δx=x总2-x总1=6 m
在这段位移内汽车以正常行驶速度做匀速直线运动,则Δt=t2-(t1+ )=25 s。
补充例题
如图所示,某个小物块以一定的初速度从斜面底端A点冲上固定的光滑斜面,斜面总长度为l,到达斜面最高点C时速度恰好为零,已知小物块运动到距斜面底端l处的B点时,所用时间为t,则小物块从B滑到C所用的时间为( )
A.0.5t B.t C.1.5t D.2t
B
法一:平均速度法
由题意知AC==,v02=2axAC,vB2=2axBC,xBC=。由以上各式可得vB=AC=,则vB正好等于AC段的平均速度,根据匀变速直线运动中中间时刻的瞬时速度等于这段位移的平均速度,可知B点是这段位移的中间时刻,因此有tBC=t,故选B。
法二:比例法
对于初速度为零的匀加速直线运动,在连续相等的时间里通过的位移之比为x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)。因为xCB∶xBA= ∶ =1∶3,而通过xBA的时间为t,所以通过xBC的时间tBC=t,故选B。
法三:逆向思维法
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面。设物体从B到C所用的时间为tBC。由运动学公式得xBC=,xAC=,又xBC=,由以上三式解得tBC=t,故选B。
法四:图像法
根据匀变速直线运动的规律,画出v-t图像,如图所示。利用相似三角形的规律,面积之比等于对应边的平方比,得=,且=,OD=t,OC=t+tBC。所以= ,解得tBC=t,故选B。
应用匀变速直线运动的推论解题的“五法”
1.一个做匀加速直线运动的物体,先后经过相距为x的A、B两点时的度分别为v和7v,从A到B的运动时间为t,则下列说法不正确的是( )
A.经过AB中点的速度为4v
B.经过AB中间时刻的速度为4v
C.通过前位移所需时间是通过后位移所需时间的2倍
D.前时间通过的位移比后时间通过的位移少1.5vt
A
物体经过AB中点的速度为,A错误;物体经过AB中间时刻的速度为,B正确;通过前位移所需时间,通过后位移所需时间,C正确;前时间通过的位移x1=·=vt,后时间通过的位移x2=·=vt,Δx=x2-x1=1.5vt,D正确。
2. (多选)物体以初速度v0做匀减速直线运动,第1 s内通过的位移为x1=3 m,第2 s内通过的位移为x2=2 m,又经过位移x3物体的速度减小为0,则下列说法中正确的是( )
A.加速度a的大小为1 m/s2
B.初速度v0的大小为2.5 m/s
C.位移x3的大小为m
D.位移x3内的平均速度大小为0.75 m/s
ACD
根据Δx=aT2,得m/s2=-1 m/s2,A正确;根据x1=v0t1+at12,得v0=3.5 m/s,B错误;第2 s末的速度v2=v0+at2=(3.5-1×2) m/s=1.5 m/s,则x3== m= m,位移x3内的平均速度大小==0.75 m/s,CD正确。
3.如图为港珠澳大桥上四段110 m的等跨钢箱连续梁桥,若汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,则( )
A.通过cd段的时间为t
B.通过ce段的时间为(2-)t
C.ae段的平均速度等于c点的瞬时速度
D.ac段的平均速度等于b点的瞬时速度
B
根据初速度为零的匀加速直线运动规律可知,汽车通过ab、bc、cd、de所用的时间之比为1∶(-1)∶(-)∶(2-),可得出通过cd段的时间为(-)t,选项A错误;通过cd段的时间为(-)t,通过de段的时间为(2-)t,则通过ce段的时间为(2-)t,选项B正确;通过ae段的时间为2t,通过b点的时刻为通过ae时间的中间时刻,故通过b点的瞬时速度等于ae段的平均速度,选项CD错误。
4. (2022·湖北高考) 我国高铁技术全球领先,乘高铁极大节省了出行时间。假设两火车站W和G间的铁路里程为1 080 km,W和G之间还均匀分布了4个车站。列车从W站始发,经停4站后到达终点站G。设普通列车的最高速度为108 km/h,高铁列车的最高速度为324 km/h。若普通列车和高铁列车在进站和出站过程中,加速度大小均为0.5 m/s2,其余行驶时间内保持各自的最高速度匀速运动,两种列车在每个车站停车时间相同,则从W到G乘高铁列车出行比乘普通列车节省的时间为( )
A.6小时25分钟 B.6小时30分钟
C.6小时35分钟 D.6小时40分钟
B
108 km/h=30 m/s,324 km/h=90 m/s,由于中间4个站均匀分布,因此节省的时间相当于在任意相邻两站间节省的时间的5倍,相邻两站间的距离x=m=2.16×105 m,普通列车加速时间t1==s=60 s,加速过程的位移x1=at12=×0.5×602 m=900 m,根据对称性可知加速与减速位移相等,可得匀速运动的时间t2==s=7 140 s,同理高铁列车加速时间t1′==s=180 s,加速过程的位移x1′=at1′2=×0.5×1802 m=8 100 m ,根据对称性可知加速与减速位移相等,可得匀速运动的时间t2′==s=2 220 s,相邻两站间节省的时间Δt=(t2+2t1)-(t2′+2t1′)=4 680 s,因此总的节省时Δt总=5Δt=4 680×5 s=23 400 s=6小时30分,故选B。
第13页 共13页
[人教版必修第一册]
1.第二章第2节,读图2.2-1,理解匀变速直线运动的速度图像是一条倾斜的直线,思考匀减速直线运动的图像是什么样的?
提示:匀减速直线运动的速度越来越小,速度图像如图甲、乙所示:
2.第二章第2节[思考与讨论]图2.2-3,从v t图像中可以看出加速度如何变化?速度如何变化?
提示:读图,相等的时间间隔Δt = Δt′,Δv>Δv′,说明加速度逐渐减小。从图像上能直接看出,物体的速度随时间增大,物体做加速度逐渐减小的变加速运动。
3.第二章第3节[拓展学习] 匀变速直线运动位移公式的推导,推导过程用到了什么思想方法?
提示:推导位移等于v t图像与t坐标轴围成的面积时,用到了微元法。
4.第二章第3节[练习与应用]第2题,汽车制动后做匀减速直线运动,求5 s内发生的位移要注意什么?
提示:先求出汽车经过多长时间停止,再根据公式计算汽车的位移,要注意刹车陷阱问题。
5.第二章第3节[练习与应用]第4题、第5题,充分理解题目涉及的情境,从实际情境中抽象出物理模型。
提示:第4题,滑跃式起飞过程:飞机初速度为0,先沿平面做匀加速运动,然后再沿斜面做匀加速运动。第5题,飞船返回舱着陆前做匀减速运动,末速度为0。
考点一 匀变速直线运动的基本规律及应用
1.匀变速直线运动的定义和分类
(1)匀变速直线运动:沿着一条直线,且 加速度 不变的运动。
(2)当a与v0 同向 时,物体做匀加速直线运动;
当a与v0 反向 时,物体做匀减速直线运动;
匀变速运动的v-t图线是一条倾斜的直线,如图所示,图线①(斜向上)为匀加速直线运动;图线②(斜向下)为匀减速直线运动。
2.三个基本公式
(1)速度与时间的关系: ;
(2)位移与时间的关系: ;
(3)速度与位移的关系 : ;
应用三个基本公式解决问题时,分析题目条件中有哪些已知量,v 0、v、a、t、x知道任意3个,可选择合适的公式求出另外2个。
题型一 基本公式和速度位移关系式的应用
如图所示,甲从A地沿平直公路由静止匀加速跑向B地,当甲前进距离为s1时,乙从距A地s2处的C点由静止出发,加速度与甲相同,最后两人同时到达B地,则A、B两地距离为( )
A. B. C. D.
B
设甲前进距离为s1时,速度为v,甲、乙匀加速直线运动的加速度为a,乙出发到达B点的时间为t,则有:vt+at2 at2=s2 s1,根据速度位移公式得,解得;则AB的距离
故选B。
题型二 刹车问题
(2022·苏州市模拟)汽车以20 m/s 的速度在平直公路上行驶,遇到紧急情况急刹车时的加速度大小为5 m/s2,则自驾驶员急踩刹车开始,经过2s与5s汽车的位移之比为( )
A.5∶4 B.4∶5 C.3∶4 D.4∶3
C
汽车速度减为零的时间t0==s=4s,刹车2s内的位移x1=v0t+at2=20×2 m-×5×22 m=30 m,由于刹车时间为4s,刹车5s内的位移等于刹车4s内的位移x2==40 m,所以经过2s与5s汽车的位移之比为3∶4,故选项C正确。
题型三 先减速后反向加速
(多选)在足够长的光滑固定斜面上,有一物体以10 m/s的初速度沿斜面向上运动,物体的加速度大小始终为5 m/s2、方向沿斜面向下,当物体的位移大小为7.5 m时,下列说法正确的是( )
A.物体运动时间可能为1s B.物体运动时间可能为3s
C.物体运动时间可能为(2+) s D.物体此时的速度大小一定为5 m/s
ABC
以沿斜面向上为正方向,则a=-5 m/s2,当物体的位移为沿斜面向上7.5 m时,x=7.5m,由运动学公式x=v0t+at2,解得t1=3 s或t2=1 s,故A、B正确.当物体的位移为沿斜面向下7.5 m时,x=-7.5 m,由x=v0t+at2,解得t3=(2+) s或t4=(2-) s(舍去),故C正确.由速度时间公式v=v0+at,解得v1=-5 m/s、v2=5 m/s、v3=-5 m/s,故D错误.
1.v0、v、a、x均为矢量,正、负号表示矢量的方向。匀变速直线运动中,通常以初速度v0的方向为正方向;当v0=0时,一般以加速度a的方向为正方向。速度、加速度、位移的方向与正方向相同时取正,相反时取负。
2.充分理解刹车问题的实际情况:①驾驶员看到前方有情况到操作刹车的时间(反应时间)车做匀速运动。②当车速减小到0以后,车会停下来,需要根据刹车时间(从开始刹车到速度减小到0的时间),判断汽车实际行驶的距离。
3.对加速度不变、先减速后反向加速的问题,求解时可分过程列式,也可对全过程列式,但必须注意x、v、a等矢量的正负号及物理意义。
1.(2023·湖南长沙市第一中学月考)如图所示,一质点做匀加速直线运动先后经过A、B、C三点,已知从A到B和从B到C速度的增加量Δv均为6 m/s,AB间的距离x1=3 m,BC间的距离x2=13 m,则该质点的加速度为( )
A.3.6 m/s2 B.4 m/s2
C.4.2 m/s2 D.4.8 m/s2
A
因为从A到B和从B到C速度的增加量Δv均为6 m/s,可知从A到B的时间和从B到C的时间相等,有Δv=aT=6 m/s,Δx=x2-x1=aT2=10 m,联立可得T= s,a=3.6 m/s2,A正确.
2.一汽车刹车做匀减速直线运动,在第二秒内的位移为3 m,第三秒内的位移为0.125 m,则汽车的加速度大小为( )
A.3 m/s2 B.3.5 m/s2
C.4 m/s2 D.4.25 m/s2
C
假设汽车第3s内已停止运动,由匀变速直线运动的推论可知,1.5s时的速度为
则2s末的速度为
第3s内的位移可表示为
联立代入数据解得
,
则第2s内的位移为
即假设符合题意。
故选C。
3.如图所示,一个小球以初速度10 m/s从斜面底端O冲上一固定斜面,A、B、C依次是斜面上的三个点,AC间距为8 m,B为AC中点。经过2 s,小球第一次通过A点,又经4 s第二次通过C点,不计一切摩擦,则下列说法正确的是( )
A.质点的加速度大小为3 m/s2
B.OA间距为8 m
C.第一次通过B点的速度大小一定为2 m/s
D.第3 s末经过B点
C
根据匀变速直线运动规律,设OA间距为x,知通过OA所用时间t=2 s,有x=v0t-at2,质点又经4s第二次通过C点,有x+8=v0(t+4)-a(t+4)2,联立可得a=2 m/s2,x=16 m,故A、B错误;B点为AC的中间位置,OB间距为x1=x+4 m=20 m,由-=-2ax1得vB=2 m/s,故C正确;第3s末小球的位移为:大于OB间距20 m,所以第3 s末小球已经越过了B点,故D错误。
考点二 匀变速直线运动的重要推论及应用
1.两个重要推论
(1)物体在一段时间内的平均速度等于这段时间 中间时刻 的瞬时速度,还等于初、末时刻速度矢量和的 一半 ,即:。(补充:中间位移的瞬时速度公式:)
(2)任意两个连续相等的时间间隔T内的位移之差为一恒量,即:Δx=x2-x1=x3-x2=…=xn-xn-1= aT2。可以推广得到xm-xn=(m-n)aT2。
2.初速度为零的匀变速直线运动的五个推论
(1)1T末、2T末、3T末……nT末瞬时速度的比为v1∶v2∶v3∶…∶vn=1∶2∶3∶…∶n 。
(2)1T内、2T内、3T内……nT内位移的比为x1∶x2∶x3∶…∶xn= 12∶22∶32∶…∶n2 。
(3)第一个T内、第二个T内、第三个T内……第n个T内位移的比为x1′∶x2′∶x3′∶…∶xn′= 1∶3∶5∶…∶(2n-1) 。
(4)从静止开始运动位移x、2x、3x……nx所用时间的比为t1∶t2∶t3∶…∶tn= 。
(5)从静止开始通过连续相等的位移所用时间的比为t1′∶t2′∶t3′∶…∶tn′=。
题型一 平均速度公式
一物体做匀加速直线运动,通过一段位移Δx所用的时间为t1,紧接着通过下一段位移Δx所用时间为t2。则物体运动的加速度为( )
A. B. C. D.
A
物体做匀加速直线运动在前一段所用的时间为,平均速度为,即为时刻的瞬时速度;
物体在后一段所用的时间为,平均速度为 ,即为时刻的瞬时速度。
速度由变化到的时间为
所以加速度为
故选A。
题型二 位移差公式
(2023·重庆市实验外国语学校高三检测)物体从静止开始做匀加速直线运动,已知第4 s内与第2 s内的位移之差是8 m,则下列说法错误的是( )
A.物体运动的加速度为4 m/s2
B.第2 s内的位移为6 m
C.第2 s末的速度为2 m/s
D.物体在0~5 s内的平均速度为10 m/s
C
根据位移差公式得x4-x2=2aT2,可知a== m/s2=4 m/s2,故A正确,不符合题意;第2 s内的位移为x2-x1=at22-at12=×4×(22-12) m=6 m,故B正确,不符合题意;第2 s末的速度为v=at2=4×2 m/s=8 m/s,故C错误,符合题意;物体在0~5 s内的平均速度=== m/s=10 m/s,故D正确,不符合题意.
题型三 初速度为零的匀变速直线运动比例式
(多选)如图所示,一冰壶以速度v垂直进入三个完全相同的矩形区域做匀减速直线运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是( )
A.v1∶v2∶v3=3∶2∶1
B.v1∶v2∶v3=∶∶1
C.t1∶t2∶t3=1∶∶
D.t1∶t2∶t3=(-)∶(-1)∶1
BD
冰壶做匀减速直线运动且末速度为零,可以将它的运动看成反向的初速度为零的匀加速直线运动。初速度为零的匀加速直线运动中通过连续三段相等位移的时间之比为1∶(-1)∶(-),故t1∶t2∶t3=(-)∶(-1)∶1,选项C错误,D正确;由v2-v02=2ax可得,初速度为零的匀加速直线运动中通过连续相等位移的速度之比为1∶∶,故v1∶v2∶v3=∶∶1,选项A错误,B正确。
题型四 车辆进出站问题
ETC是电子不停车收费系统的简称,汽车分别通过ETC通道和人工收费通道的流程如图所示。假设汽车以v1=12 m/s的速度朝收费站沿直线行驶,如果过ETC通道,需要在距收费站中心线前d=10 m处正好匀减速至v2=4 m/s,匀速通过中心线后,再匀加速至v1正常行驶;如果过人工收费通道,需要恰好在中心线处匀减速至零,经过t0=20 s缴费成功后,再启动汽车匀加速至v1正常行驶,设汽车加速和减速过程中的加速度大小均为1 m/s2。
求:
(1)汽车过ETC通道时,从开始减速到恢复正常行驶过程中的位移大小;
(2)汽车过人工收费通道时,应在离收费站中心线多远处开始减速;
(3)汽车过ETC通道比过人工收费通道节约的时间。
(1)138 m (2)72 m (3)25 s
(1)过ETC通道时,减速的位移和加速的位移相等,则x1==64 m
故总的位移x总1=2x1+d=138 m。
(2)过人工收费通道时,开始减速时距离中心线为
x2==72 m。
(3)过ETC通道的时间
t1=×2+ =18.5 s
过人工收费通道的时间
t2=×2+t0=44 s
x总2=2x2=144 m
二者的位移差Δx=x总2-x总1=6 m
在这段位移内汽车以正常行驶速度做匀速直线运动,则Δt=t2-(t1+ )=25 s。
补充例题
如图所示,某个小物块以一定的初速度从斜面底端A点冲上固定的光滑斜面,斜面总长度为l,到达斜面最高点C时速度恰好为零,已知小物块运动到距斜面底端l处的B点时,所用时间为t,则小物块从B滑到C所用的时间为( )
A.0.5t B.t C.1.5t D.2t
B
法一:平均速度法
由题意知AC==,v02=2axAC,vB2=2axBC,xBC=。由以上各式可得vB=AC=,则vB正好等于AC段的平均速度,根据匀变速直线运动中中间时刻的瞬时速度等于这段位移的平均速度,可知B点是这段位移的中间时刻,因此有tBC=t,故选B。
法二:比例法
对于初速度为零的匀加速直线运动,在连续相等的时间里通过的位移之比为x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)。因为xCB∶xBA= ∶ =1∶3,而通过xBA的时间为t,所以通过xBC的时间tBC=t,故选B。
法三:逆向思维法
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面。设物体从B到C所用的时间为tBC。由运动学公式得xBC=,xAC=,又xBC=,由以上三式解得tBC=t,故选B。
法四:图像法
根据匀变速直线运动的规律,画出v-t图像,如图所示。利用相似三角形的规律,面积之比等于对应边的平方比,得=,且=,OD=t,OC=t+tBC。所以= ,解得tBC=t,故选B。
应用匀变速直线运动的推论解题的“五法”
1.一个做匀加速直线运动的物体,先后经过相距为x的A、B两点时的度分别为v和7v,从A到B的运动时间为t,则下列说法不正确的是( )
A.经过AB中点的速度为4v
B.经过AB中间时刻的速度为4v
C.通过前位移所需时间是通过后位移所需时间的2倍
D.前时间通过的位移比后时间通过的位移少1.5vt
A
物体经过AB中点的速度为,A错误;物体经过AB中间时刻的速度为,B正确;通过前位移所需时间,通过后位移所需时间,C正确;前时间通过的位移x1=·=vt,后时间通过的位移x2=·=vt,Δx=x2-x1=1.5vt,D正确。
2. (多选)物体以初速度v0做匀减速直线运动,第1 s内通过的位移为x1=3 m,第2 s内通过的位移为x2=2 m,又经过位移x3物体的速度减小为0,则下列说法中正确的是( )
A.加速度a的大小为1 m/s2
B.初速度v0的大小为2.5 m/s
C.位移x3的大小为m
D.位移x3内的平均速度大小为0.75 m/s
ACD
根据Δx=aT2,得m/s2=-1 m/s2,A正确;根据x1=v0t1+at12,得v0=3.5 m/s,B错误;第2 s末的速度v2=v0+at2=(3.5-1×2) m/s=1.5 m/s,则x3== m= m,位移x3内的平均速度大小==0.75 m/s,CD正确。
3.如图为港珠澳大桥上四段110 m的等跨钢箱连续梁桥,若汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,则( )
A.通过cd段的时间为t
B.通过ce段的时间为(2-)t
C.ae段的平均速度等于c点的瞬时速度
D.ac段的平均速度等于b点的瞬时速度
B
根据初速度为零的匀加速直线运动规律可知,汽车通过ab、bc、cd、de所用的时间之比为1∶(-1)∶(-)∶(2-),可得出通过cd段的时间为(-)t,选项A错误;通过cd段的时间为(-)t,通过de段的时间为(2-)t,则通过ce段的时间为(2-)t,选项B正确;通过ae段的时间为2t,通过b点的时刻为通过ae时间的中间时刻,故通过b点的瞬时速度等于ae段的平均速度,选项CD错误。
4. (2022·湖北高考) 我国高铁技术全球领先,乘高铁极大节省了出行时间。假设两火车站W和G间的铁路里程为1 080 km,W和G之间还均匀分布了4个车站。列车从W站始发,经停4站后到达终点站G。设普通列车的最高速度为108 km/h,高铁列车的最高速度为324 km/h。若普通列车和高铁列车在进站和出站过程中,加速度大小均为0.5 m/s2,其余行驶时间内保持各自的最高速度匀速运动,两种列车在每个车站停车时间相同,则从W到G乘高铁列车出行比乘普通列车节省的时间为( )
A.6小时25分钟 B.6小时30分钟
C.6小时35分钟 D.6小时40分钟
B
108 km/h=30 m/s,324 km/h=90 m/s,由于中间4个站均匀分布,因此节省的时间相当于在任意相邻两站间节省的时间的5倍,相邻两站间的距离x=m=2.16×105 m,普通列车加速时间t1==s=60 s,加速过程的位移x1=at12=×0.5×602 m=900 m,根据对称性可知加速与减速位移相等,可得匀速运动的时间t2==s=7 140 s,同理高铁列车加速时间t1′==s=180 s,加速过程的位移x1′=at1′2=×0.5×1802 m=8 100 m ,根据对称性可知加速与减速位移相等,可得匀速运动的时间t2′==s=2 220 s,相邻两站间节省的时间Δt=(t2+2t1)-(t2′+2t1′)=4 680 s,因此总的节省时Δt总=5Δt=4 680×5 s=23 400 s=6小时30分,故选B。
第13页 共13页
同课章节目录
