2023-2024学年人教版数学八年级上册第十一章 三角形 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册第十一章 三角形 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 212.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 12:53:59 | ||
图片预览


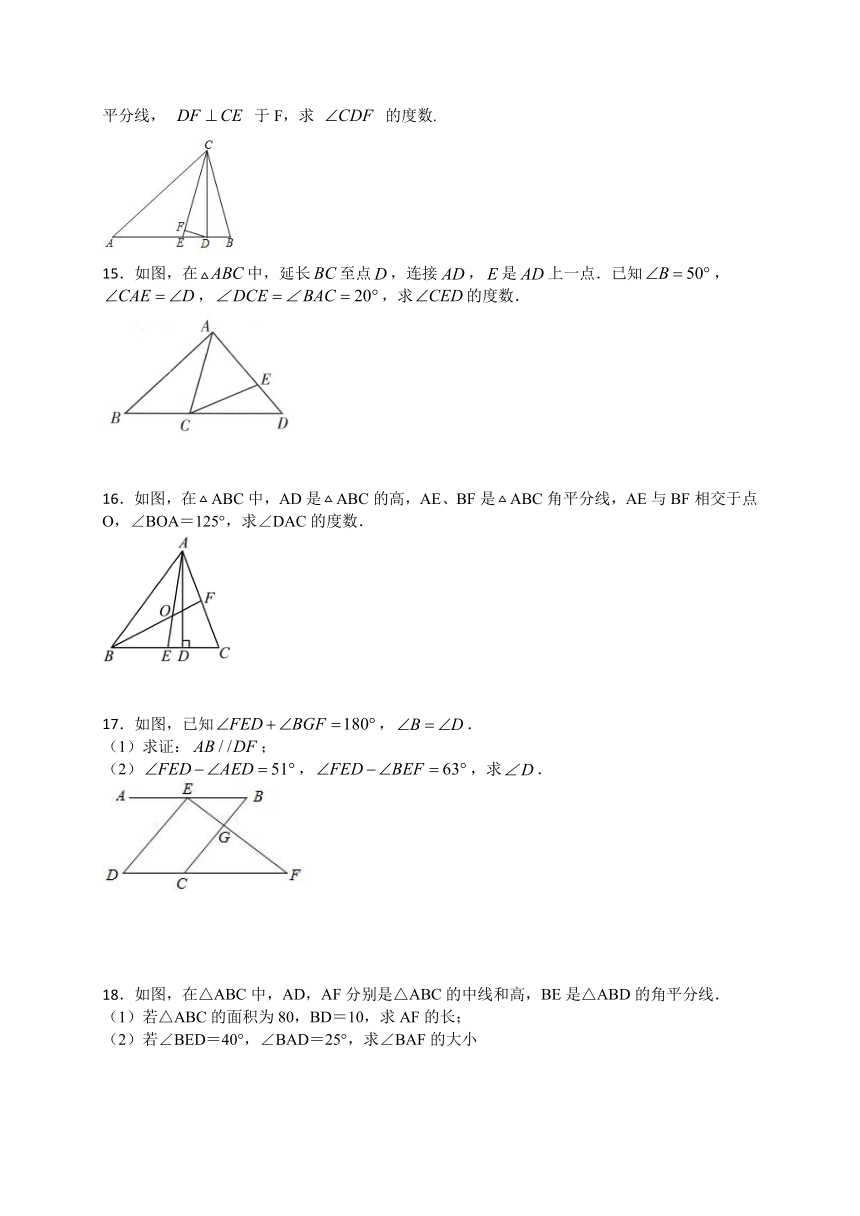
文档简介
第十一章 三角形 单元练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列每组数分别是小木棒的长度,用它们能摆成三角形的是( )
A.3、4、8 B.8、7、15 C.13、12、20 D.5、5、11
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
3.下列四个图形中,线段BD是△ABC的高的是( )
A. B. C. D.
4.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转,某一指令规定:机器人先向前行走2米,然后左转45°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了( )
A.14米 B.15米 C.16米 D.17米
5.如图,在中,,是的高线,是的角平分线,则的度数是( )
A. B. C. D.
6.如图,已知,是两条相交线段,连结,,分别作和的平分线相交于点,若,,则的度数为
A. B. C. D.
7.如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )
A.12 B.14 C.16 D.18
8.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知正多边形的一个外角等于60°,则这个正多边形的内角和的度数为 .
10.AE是△ABC的中线(E在BC所在直线上),且BE=4cm,那么BC= cm.
11.如图,直线AB CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是 cm.
12.如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD= .
13.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为 .
三、解答题:(本题共5题,共45分)
14.如图,在 中, , ,CD是AB边上的高,CE是 的平分线, 于F,求 的度数.
15.如图,在中,延长至点,连接,是上一点.已知,,,求的度数.
16.如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17.如图,已知,.
(1)求证:;
(2),,求.
18.如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若△ABC的面积为80,BD=10,求AF的长;
(2)若∠BED=40°,∠BAD=25°,求∠BAF的大小
参考答案:
1.C 2.C 3.C 4.C 5.A 6.B 7.D 8.C
9.720°
10.8
11.12
12.65°
13.2或4
14.解: , ,
,
平分 ,
,
,
, ,
,
.
15.解:,,
,
,
16.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
17.(1)证明:∵∠FED+∠BGF=180°,∠BGF=∠EGC,
∴∠FED+∠EGC=180°,
∴BC∥ED,
∴∠B+∠BED=180°,
∵∠B=∠D,
∴∠BED+∠D=180°,
∴AB∥DF;
(2)解:
设∠FED=x,
∵∠FED-∠AED=51°,∠FED-∠BEF=63°,
∴∠AED=x-51°,∠BEF=x-63°,
∵∠AED+∠FED+∠BEF=180°,
∴x-51°+x+x-63°=180°,
∴x=98°,
∴∠AED=98°-51°=47°,
∵AB∥DF,
∴∠D=∠AED=47°.
18.(1)解:∵AD是△ABC的中线,BD=10,
∴BC=2BD=1×10=20,
∵AF是△ABC的高,△ABC的面积为80,
∴BC AF=×20 AF=80,
∴AF=8;
(2)解:在△ABE中,∠BED为它的一个外角,且∠BED=40°,∠BAD=25°,
∴∠ABE=∠BED﹣∠BAD=40°﹣25°=15°,
∵BE是△ABD的角平分线,
∴∠ABC=2∠ABE=2×15°=30°,
∵AF是△ABC的高,
∴∠AFB=90°.
∴∠BAF=90°﹣∠ABC=90°﹣30°=60°
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列每组数分别是小木棒的长度,用它们能摆成三角形的是( )
A.3、4、8 B.8、7、15 C.13、12、20 D.5、5、11
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
3.下列四个图形中,线段BD是△ABC的高的是( )
A. B. C. D.
4.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转,某一指令规定:机器人先向前行走2米,然后左转45°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了( )
A.14米 B.15米 C.16米 D.17米
5.如图,在中,,是的高线,是的角平分线,则的度数是( )
A. B. C. D.
6.如图,已知,是两条相交线段,连结,,分别作和的平分线相交于点,若,,则的度数为
A. B. C. D.
7.如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )
A.12 B.14 C.16 D.18
8.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知正多边形的一个外角等于60°,则这个正多边形的内角和的度数为 .
10.AE是△ABC的中线(E在BC所在直线上),且BE=4cm,那么BC= cm.
11.如图,直线AB CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是 cm.
12.如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD= .
13.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为 .
三、解答题:(本题共5题,共45分)
14.如图,在 中, , ,CD是AB边上的高,CE是 的平分线, 于F,求 的度数.
15.如图,在中,延长至点,连接,是上一点.已知,,,求的度数.
16.如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17.如图,已知,.
(1)求证:;
(2),,求.
18.如图,在△ABC中,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若△ABC的面积为80,BD=10,求AF的长;
(2)若∠BED=40°,∠BAD=25°,求∠BAF的大小
参考答案:
1.C 2.C 3.C 4.C 5.A 6.B 7.D 8.C
9.720°
10.8
11.12
12.65°
13.2或4
14.解: , ,
,
平分 ,
,
,
, ,
,
.
15.解:,,
,
,
16.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
17.(1)证明:∵∠FED+∠BGF=180°,∠BGF=∠EGC,
∴∠FED+∠EGC=180°,
∴BC∥ED,
∴∠B+∠BED=180°,
∵∠B=∠D,
∴∠BED+∠D=180°,
∴AB∥DF;
(2)解:
设∠FED=x,
∵∠FED-∠AED=51°,∠FED-∠BEF=63°,
∴∠AED=x-51°,∠BEF=x-63°,
∵∠AED+∠FED+∠BEF=180°,
∴x-51°+x+x-63°=180°,
∴x=98°,
∴∠AED=98°-51°=47°,
∵AB∥DF,
∴∠D=∠AED=47°.
18.(1)解:∵AD是△ABC的中线,BD=10,
∴BC=2BD=1×10=20,
∵AF是△ABC的高,△ABC的面积为80,
∴BC AF=×20 AF=80,
∴AF=8;
(2)解:在△ABE中,∠BED为它的一个外角,且∠BED=40°,∠BAD=25°,
∴∠ABE=∠BED﹣∠BAD=40°﹣25°=15°,
∵BE是△ABD的角平分线,
∴∠ABC=2∠ABE=2×15°=30°,
∵AF是△ABC的高,
∴∠AFB=90°.
∴∠BAF=90°﹣∠ABC=90°﹣30°=60°
