2023-2024学年人教版数学九年级上册第二十二章二次函数 单元练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级上册第二十二章二次函数 单元练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 13:10:58 | ||
图片预览



文档简介
第二十二章二次函数 单元练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.若y=ax2﹣x+2是y关于x的二次函数,则a的取值范围是( )
A.a>0 B.a<0 C.a≠0 D.a≠2
2.将抛物线y=(x-6)2+5的图象向左平移1个单位,再向上平移2个单位得到抛物线的解析式是( )
A.y=(x-5)2+7 B.y=(x-5)2-3
C.y=(x-7)2+7 D.y=(x-7)2-3
3.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y= (x+3)2 B.y= (x+3)2
C.y= (x﹣3)2 D.y= (x﹣3)2
4.如图, 抛物线的对称轴是直线, 且经过点, 则 的值为( )
A.0 B.-1 C.1 D.2
5.若二次函数y=ax2+bx+c的图象与x轴交于A和B两点,顶点为C,且b2﹣4ac=4,则∠ACB的度数为( )
A.120° B.90° C.60° D.30°
6.若二次函数 的图象的顶点在第一象限,且经过点(0,1)和(-1,0),则 的值的变化范围是( )
A. B. C. D.
7.如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(3,0),对称轴为直线x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c>0;④当y>0时,﹣1<x<3;⑤b<c.其中正确的个数是( )
A.2 B.3 C.4 D.5
8.如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
二、填空题:(本题共5小题,每小题3分,共15分.)
9.抛物线上的点到x轴最短的距离是 .
10.已知二次函数 ,在-1≤x≤1的取值范围内,有最小值是 。
11.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 。
12.如图抛物线y=x2+2x﹣3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
13.如图,在平面直角坐标系中,点A、B的坐标分别为、,抛物线的顶点P在线段上,与x轴相交于C、D两点,设点C、D的横坐标分别为、,且.若的最小值是-2,则的最大值是 .
三、解答题:(本题共5题,共45分)
14.已知:抛物线y=5x2+(m﹣3)x与y=﹣2x﹣m交于点A(x1,y1)和点B(x2,y2),且有(x1﹣x2)2= ,求m的值.
15.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
16.一次足球训练中,小明从球门正前方8m的处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素)。
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方2.25m处
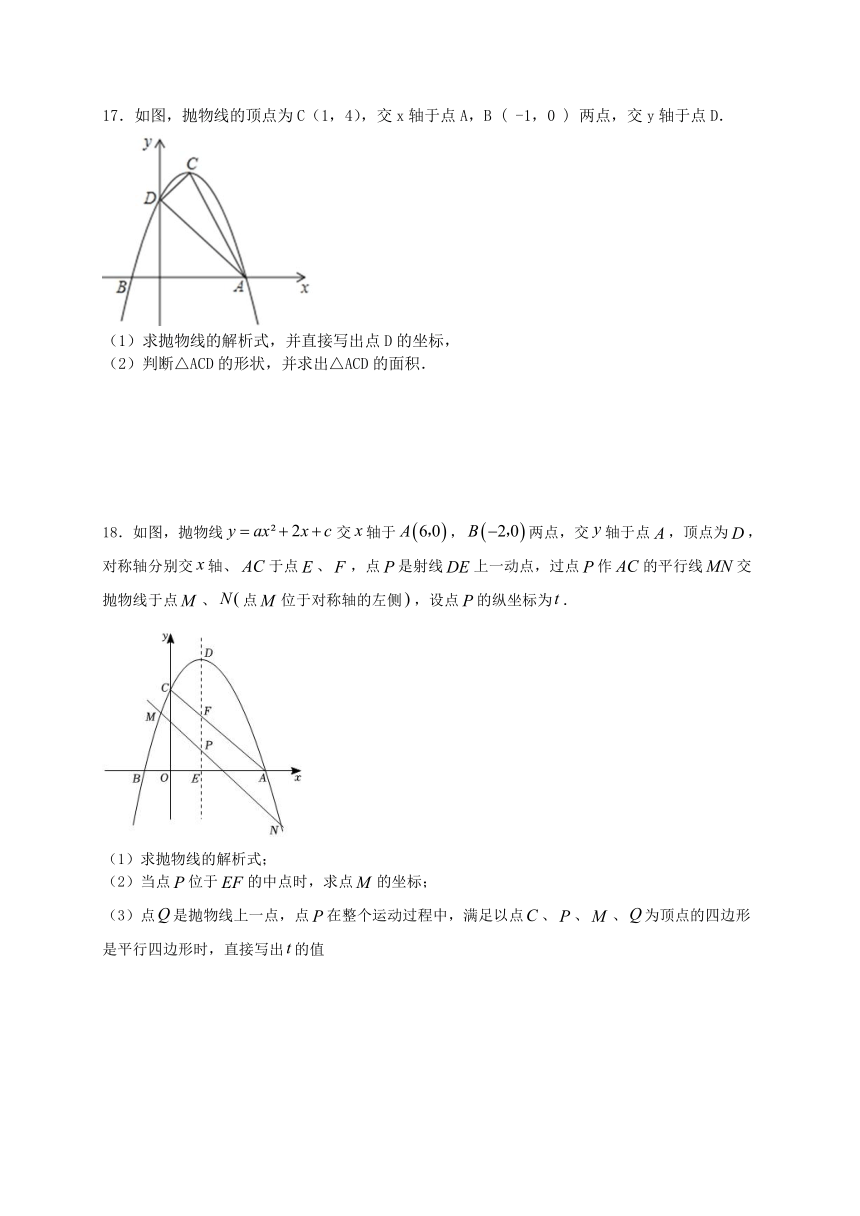
17.如图,抛物线的顶点为C(1,4),交x轴于点A,B ( -1,0 ) 两点,交y轴于点D.
(1)求抛物线的解析式,并直接写出点D的坐标,
(2)判断△ACD的形状,并求出△ACD的面积.
18.如图,抛物线交轴于,两点,交轴于点,顶点为,对称轴分别交轴、于点、,点是射线上一动点,过点作的平行线交抛物线于点、点位于对称轴的左侧,设点的纵坐标为.
(1)求抛物线的解析式;
(2)当点位于的中点时,求点的坐标;
(3)点是抛物线上一点,点在整个运动过程中,满足以点、、、为顶点的四边形是平行四边形时,直接写出的值
参考答案:
1.C 2.A 3.C 4.A 5.B 6.A 7.B 8.B
9.3
10.-1
11.012.
13.3
14.解:∵抛物线y=5x2+(m﹣3)x与y=﹣2x﹣m交于点A(x1,y1)和点B(x2,y2),
∴5x2+(m﹣3)x=﹣2x﹣m,
化简,得
5x2+(m﹣1)x+m=0,
∴x1+x2=﹣ = ,x1x2= ,
∵(x1﹣x2)2= ,(x1﹣x2)2=(x1+x2)2﹣4x1x2,
∴(x1+x2)2﹣4x1x2= ,
∴( )2﹣4× = ,
解得,m1=24,m2=﹣2,
即m的值是24或﹣2
15.解:(1)y=w(x﹣20)
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
则y=﹣2x2+120x﹣1600.
由题意,有,
解得20≤x≤40.
故y与x的函数关系式为:y=﹣2x2+120x﹣1600,自变量x的取值范围是20≤x≤40;
(2)∵y=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∴当x=30时,y有最大值200.
故当销售价定为30元/千克时,每天可获最大销售利润200元;
(3)当y=150时,可得方程﹣2x2+120x﹣1600=150,
整理,得x2﹣60x+875=0,
解得x1=25,x2=35.
∵物价部门规定这种产品的销售价不得高于28元/千克,∴x2=35不合题意,应舍去.
故当销售价定为25元/千克时,该农户每天可获得销售利润150元.
16.(1)解:由题意,得抛物线的顶点坐标为(2,3),
设抛物线为y=a(x-2)2+3,把点A(8,0)代入,
得36a+3=0,
解得,
抛物线的函数表达式为,
当x=0时,
∴球不能射进球门;
(2)解:如图,设小明带球向正后方移动m米,则移动后的抛物线为,
把点(0,2.25)代入得,
解得(舍去),,
当时他应该带球向正后方移动1米射门.
17.(1)解:∵抛物线的顶点坐标为(1,4),∴可设抛物线解析式为,∵与轴交于点B(-1,0), ∴,解得,∴抛物线解析式为,∵抛物线交y轴于点D,∴D点坐标为(0,3)
(2)解:由顶点C坐标(1,4)可知对称轴是直线x=1,点B(-1,0)和点A是对称点,∴点A(3,0),,∴△ACD是以AC为斜边的直角三角形.
18.(1)解:将点,代入抛物线解析式可得,,
解得,,
抛物线的解析式为:;
(2)解:点,点,
直线解析式为,
当时,,
点,
点位于的中点,
点,
设直线解析式为,
,
,
直线解析式为,
联立方程组可得:,
解得:或舍去,
点;
(3)解:若为边,
以点,,,为顶点的四边形是平行四边形,
,,
又,
点与点重合,
,,
,,
,
;
若为对角线,
四边形是平行四边形,
,,,
,,
设点,则点,
,
,
,
舍去,,
;
综上所述:或
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.若y=ax2﹣x+2是y关于x的二次函数,则a的取值范围是( )
A.a>0 B.a<0 C.a≠0 D.a≠2
2.将抛物线y=(x-6)2+5的图象向左平移1个单位,再向上平移2个单位得到抛物线的解析式是( )
A.y=(x-5)2+7 B.y=(x-5)2-3
C.y=(x-7)2+7 D.y=(x-7)2-3
3.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y= (x+3)2 B.y= (x+3)2
C.y= (x﹣3)2 D.y= (x﹣3)2
4.如图, 抛物线的对称轴是直线, 且经过点, 则 的值为( )
A.0 B.-1 C.1 D.2
5.若二次函数y=ax2+bx+c的图象与x轴交于A和B两点,顶点为C,且b2﹣4ac=4,则∠ACB的度数为( )
A.120° B.90° C.60° D.30°
6.若二次函数 的图象的顶点在第一象限,且经过点(0,1)和(-1,0),则 的值的变化范围是( )
A. B. C. D.
7.如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(3,0),对称轴为直线x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c>0;④当y>0时,﹣1<x<3;⑤b<c.其中正确的个数是( )
A.2 B.3 C.4 D.5
8.如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
二、填空题:(本题共5小题,每小题3分,共15分.)
9.抛物线上的点到x轴最短的距离是 .
10.已知二次函数 ,在-1≤x≤1的取值范围内,有最小值是 。
11.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 。
12.如图抛物线y=x2+2x﹣3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
13.如图,在平面直角坐标系中,点A、B的坐标分别为、,抛物线的顶点P在线段上,与x轴相交于C、D两点,设点C、D的横坐标分别为、,且.若的最小值是-2,则的最大值是 .
三、解答题:(本题共5题,共45分)
14.已知:抛物线y=5x2+(m﹣3)x与y=﹣2x﹣m交于点A(x1,y1)和点B(x2,y2),且有(x1﹣x2)2= ,求m的值.
15.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
16.一次足球训练中,小明从球门正前方8m的处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素)。
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方2.25m处
17.如图,抛物线的顶点为C(1,4),交x轴于点A,B ( -1,0 ) 两点,交y轴于点D.
(1)求抛物线的解析式,并直接写出点D的坐标,
(2)判断△ACD的形状,并求出△ACD的面积.
18.如图,抛物线交轴于,两点,交轴于点,顶点为,对称轴分别交轴、于点、,点是射线上一动点,过点作的平行线交抛物线于点、点位于对称轴的左侧,设点的纵坐标为.
(1)求抛物线的解析式;
(2)当点位于的中点时,求点的坐标;
(3)点是抛物线上一点,点在整个运动过程中,满足以点、、、为顶点的四边形是平行四边形时,直接写出的值
参考答案:
1.C 2.A 3.C 4.A 5.B 6.A 7.B 8.B
9.3
10.-1
11.0
13.3
14.解:∵抛物线y=5x2+(m﹣3)x与y=﹣2x﹣m交于点A(x1,y1)和点B(x2,y2),
∴5x2+(m﹣3)x=﹣2x﹣m,
化简,得
5x2+(m﹣1)x+m=0,
∴x1+x2=﹣ = ,x1x2= ,
∵(x1﹣x2)2= ,(x1﹣x2)2=(x1+x2)2﹣4x1x2,
∴(x1+x2)2﹣4x1x2= ,
∴( )2﹣4× = ,
解得,m1=24,m2=﹣2,
即m的值是24或﹣2
15.解:(1)y=w(x﹣20)
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
则y=﹣2x2+120x﹣1600.
由题意,有,
解得20≤x≤40.
故y与x的函数关系式为:y=﹣2x2+120x﹣1600,自变量x的取值范围是20≤x≤40;
(2)∵y=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∴当x=30时,y有最大值200.
故当销售价定为30元/千克时,每天可获最大销售利润200元;
(3)当y=150时,可得方程﹣2x2+120x﹣1600=150,
整理,得x2﹣60x+875=0,
解得x1=25,x2=35.
∵物价部门规定这种产品的销售价不得高于28元/千克,∴x2=35不合题意,应舍去.
故当销售价定为25元/千克时,该农户每天可获得销售利润150元.
16.(1)解:由题意,得抛物线的顶点坐标为(2,3),
设抛物线为y=a(x-2)2+3,把点A(8,0)代入,
得36a+3=0,
解得,
抛物线的函数表达式为,
当x=0时,
∴球不能射进球门;
(2)解:如图,设小明带球向正后方移动m米,则移动后的抛物线为,
把点(0,2.25)代入得,
解得(舍去),,
当时他应该带球向正后方移动1米射门.
17.(1)解:∵抛物线的顶点坐标为(1,4),∴可设抛物线解析式为,∵与轴交于点B(-1,0), ∴,解得,∴抛物线解析式为,∵抛物线交y轴于点D,∴D点坐标为(0,3)
(2)解:由顶点C坐标(1,4)可知对称轴是直线x=1,点B(-1,0)和点A是对称点,∴点A(3,0),,∴△ACD是以AC为斜边的直角三角形.
18.(1)解:将点,代入抛物线解析式可得,,
解得,,
抛物线的解析式为:;
(2)解:点,点,
直线解析式为,
当时,,
点,
点位于的中点,
点,
设直线解析式为,
,
,
直线解析式为,
联立方程组可得:,
解得:或舍去,
点;
(3)解:若为边,
以点,,,为顶点的四边形是平行四边形,
,,
又,
点与点重合,
,,
,,
,
;
若为对角线,
四边形是平行四边形,
,,,
,,
设点,则点,
,
,
,
舍去,,
;
综上所述:或
同课章节目录
