2023-2024学年人教版数学九年级上册第二十三章旋转 单元练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级上册第二十三章旋转 单元练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 289.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览


文档简介
第二十三章旋转 单元练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.如图所示的四个图案,能通过基本图形旋转得到的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A.2种 B.3种 C.4种 D.5种
3.如图,△ABC绕着点O逆时针旋转到△DEF的位置,则旋转中心及旋转角分别是( )
A.点B, ∠ABO B.点O, ∠AOB C.点B,∠BOE D.点O,∠AOD
4.二次函数y=-2x2+1的图象如图所示,将其绕坐标原点O旋转180°,则旋转后的抛物线的解析式为( )
A.y=-2x2-1 B.y=2x2+1 C.y=2x2 D.y=2x2-1
5.如图,将 绕点A逆时针旋转得到 ,延长 交 于点D,若 ,则 的度数是( )
A. B. C. D.
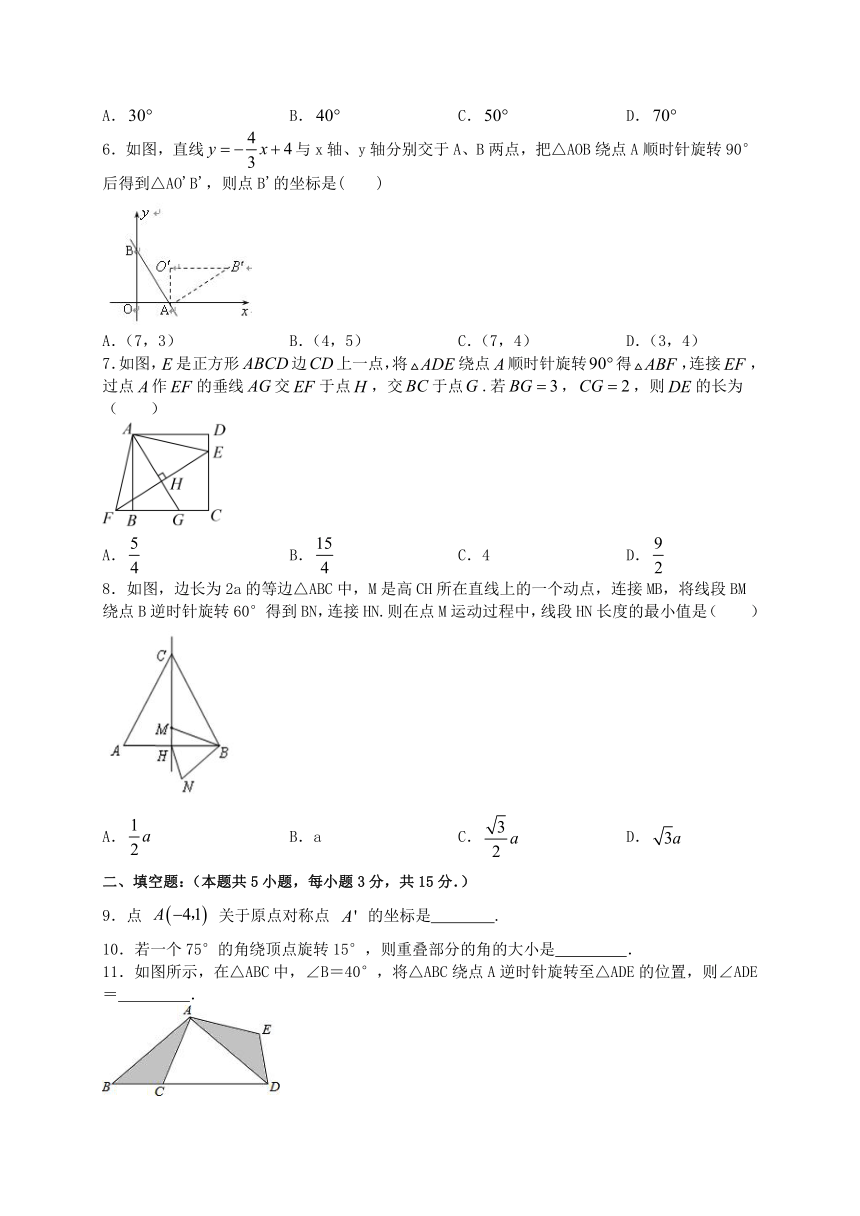
6.如图,直线与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO'B',则点B'的坐标是( )
A.(7,3) B.(4,5) C.(7,4) D.(3,4)
7.如图,是正方形边上一点,将绕点顺时针旋转得,连接,过点作的垂线交于点,交于点.若,,则的长为( )
A. B. C.4 D.
8.如图,边长为2a的等边△ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
A. B.a C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.点 关于原点对称点 的坐标是 .
10.若一个75°的角绕顶点旋转15°,则重叠部分的角的大小是 .
11.如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE的位置,则∠ADE= .
12.如图,已知在△ABC中,AB=AC=4,∠BAC=30°,将△ABC绕点A顺时针旋转,使点B落在点B1处,点C落在点C1处,且BB1⊥AC.联结B1C和C1C,那么△B1C1C的面积等于 .
13.如图,已知中,,,将绕A点逆时针旋转得到,以下结论:①,②,③,④,其中正确结论的序号是 .
三、解答题:(本题共5题,共45分)
14.在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);
(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
15.如图,△ABC中,∠BAC=120o,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60o后到△ECD的位置。若AB=6,AC=4,求∠BAD的度数和AD的长.
16.如图,四边形中,,是对角线,是等边三角形.线段绕点C顺时针旋转得到线段,连接.求证:.
17.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
18.△ABC和△ECD都是等边三角形
(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
参考答案:
1.D 2.C 3.D 4.D 5.B 6.A 7.A 8.A
9.(4,-1)
10.60°
11.40°
12.
13.①②④
14.(1)解:如图所示:
或
(2)解:如图所示:
15.解:由旋转可知:△ABD≌△ECD
∴AB=EC=6,∠BAD=∠E,AD=ED
∵∠ADE=60°
∴△ADE是等边三角形
∴AE=AD
∠E=∠DAE=60°
∴∠BAD=60°
∵∠BAC=120°
∴∠DAC=60°=∠DAE
∴C在AE上
∴AD=AC+CE=4+6=10
16.证明:由旋转可知,,
是等边三角形,
,,
即,
在和中,
,
,
.
17.(1)解:FG⊥ED.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,
∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,
∴∠GFE=∠A,
∵∠ABC=90°,
∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°,
∴∠FHE=90°,
∴FG⊥ED;
(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,
∴∠BCG=∠CBE=90°,
∴四边形BCGE是矩形,
∵CB=BE,
∴四边形CBEG是正方形
18.解:
(1)∵△ABC和△ECD都是等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°.
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE.
∴△ACD≌△BCE.
∴AD=BE.
(2)BC垂直平分DE,理由如下:
如图,
延长BC交DE于M,
∵∠ACB=60°,∠ACE=90°,
∴∠ECM=180°-∠ACB-∠ACE=30°.
∵∠DCM=∠ECD-∠ECM=30°,
∴∠ECM=∠DCM.
∵△ECD是等边三角形,
∴CM垂直平分DE,即BC垂直平分DE
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.如图所示的四个图案,能通过基本图形旋转得到的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A.2种 B.3种 C.4种 D.5种
3.如图,△ABC绕着点O逆时针旋转到△DEF的位置,则旋转中心及旋转角分别是( )
A.点B, ∠ABO B.点O, ∠AOB C.点B,∠BOE D.点O,∠AOD
4.二次函数y=-2x2+1的图象如图所示,将其绕坐标原点O旋转180°,则旋转后的抛物线的解析式为( )
A.y=-2x2-1 B.y=2x2+1 C.y=2x2 D.y=2x2-1
5.如图,将 绕点A逆时针旋转得到 ,延长 交 于点D,若 ,则 的度数是( )
A. B. C. D.
6.如图,直线与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO'B',则点B'的坐标是( )
A.(7,3) B.(4,5) C.(7,4) D.(3,4)
7.如图,是正方形边上一点,将绕点顺时针旋转得,连接,过点作的垂线交于点,交于点.若,,则的长为( )
A. B. C.4 D.
8.如图,边长为2a的等边△ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
A. B.a C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.点 关于原点对称点 的坐标是 .
10.若一个75°的角绕顶点旋转15°,则重叠部分的角的大小是 .
11.如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE的位置,则∠ADE= .
12.如图,已知在△ABC中,AB=AC=4,∠BAC=30°,将△ABC绕点A顺时针旋转,使点B落在点B1处,点C落在点C1处,且BB1⊥AC.联结B1C和C1C,那么△B1C1C的面积等于 .
13.如图,已知中,,,将绕A点逆时针旋转得到,以下结论:①,②,③,④,其中正确结论的序号是 .
三、解答题:(本题共5题,共45分)
14.在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);
(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
15.如图,△ABC中,∠BAC=120o,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60o后到△ECD的位置。若AB=6,AC=4,求∠BAD的度数和AD的长.
16.如图,四边形中,,是对角线,是等边三角形.线段绕点C顺时针旋转得到线段,连接.求证:.
17.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
18.△ABC和△ECD都是等边三角形
(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
参考答案:
1.D 2.C 3.D 4.D 5.B 6.A 7.A 8.A
9.(4,-1)
10.60°
11.40°
12.
13.①②④
14.(1)解:如图所示:
或
(2)解:如图所示:
15.解:由旋转可知:△ABD≌△ECD
∴AB=EC=6,∠BAD=∠E,AD=ED
∵∠ADE=60°
∴△ADE是等边三角形
∴AE=AD
∠E=∠DAE=60°
∴∠BAD=60°
∵∠BAC=120°
∴∠DAC=60°=∠DAE
∴C在AE上
∴AD=AC+CE=4+6=10
16.证明:由旋转可知,,
是等边三角形,
,,
即,
在和中,
,
,
.
17.(1)解:FG⊥ED.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,
∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,
∴∠GFE=∠A,
∵∠ABC=90°,
∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°,
∴∠FHE=90°,
∴FG⊥ED;
(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,
∴∠BCG=∠CBE=90°,
∴四边形BCGE是矩形,
∵CB=BE,
∴四边形CBEG是正方形
18.解:
(1)∵△ABC和△ECD都是等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°.
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE.
∴△ACD≌△BCE.
∴AD=BE.
(2)BC垂直平分DE,理由如下:
如图,
延长BC交DE于M,
∵∠ACB=60°,∠ACE=90°,
∴∠ECM=180°-∠ACB-∠ACE=30°.
∵∠DCM=∠ECD-∠ECM=30°,
∴∠ECM=∠DCM.
∵△ECD是等边三角形,
∴CM垂直平分DE,即BC垂直平分DE
同课章节目录
