苏科版八年级上册2.5等腰三角形的轴对称性(等腰三角形的分类讨论 )学案(无答案)
文档属性
| 名称 | 苏科版八年级上册2.5等腰三角形的轴对称性(等腰三角形的分类讨论 )学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 14:34:47 | ||
图片预览


文档简介
2.5等腰三角形的轴对称性(等腰三角形的分类讨论 )
【学习目标】
1.掌握等腰三角形分类讨论的方法;
2.举一反三,利用等腰三角形的性质,理解运用在动点问题中.
【要点梳理】
等腰三角形的分类讨论
遇角需讨论:顶角和底角;
遇边需讨论:底边和腰;
遇高需讨论:形内和形外.
【典型例题】
类型一、等腰三角形的分类讨论求角或边
1.等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的腰长为( )
A.3cm B.6cm C.3cm或6cm D.3cm或9cm
举一反三:
【变式1】已知△ABC是等腰三角形,若∠A=50°,则△ABC的顶角度数是( )
A.50° B.50°或80° C.80° D.50°或65°
【变式2】已知等腰三角形一腰的垂直平分线与另一腰所在的直线的夹角为40°,则此等腰三角形的顶角是( )
A.50° B.130° C.50°或 140° D.50°或 130°
【变式3】一个等腰三角形一个内角是另一个内角的2倍,则这个三角形底角为( )
A.72°或45° B.45°或36° C.36°或45° D.72°或90°
【变式4】在等腰中,,中线将这个三角形的周长分为和的两个部分,则这个等腰三角形的底边长为( )
A. B. C.或 D.或
【变式5】等腰三角形一腰上的高与另一腰的夹角为,则该等腰三角形顶角的度数为( )
B. C. D.或
类型二、 三角形内的等腰三角形分类讨论
2.Rt△ACB中,∠C=90°,∠A=30°,在直线BC或直线AC上找到一点P,使△PAB是等腰三角形,则满足条件的点P的个数是( )
4 B.6 C.7 D.8
举一反三:
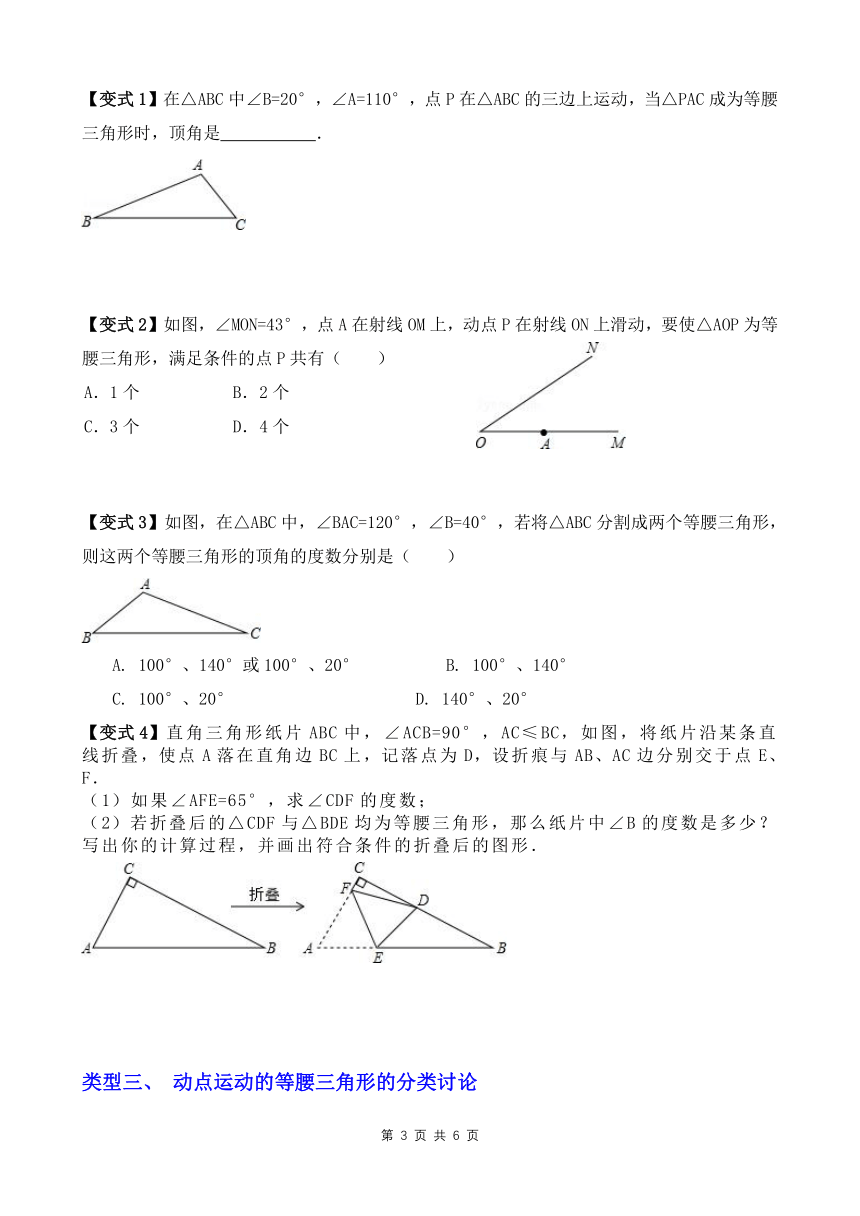
【变式1】在△ABC中∠B=20°,∠A=110°,点P在△ABC的三边上运动,当△PAC成为等腰三角形时,顶角是 .
【变式2】如图,∠MON=43°,点A在射线OM上,动点P在射线ON上滑动,要使△AOP为等腰三角形,满足条件的点P共有( )
A. 1个 B. 2个
C. 3个 D. 4个
【变式3】如图,在△ABC中,∠BAC=120°,∠B=40°,若将△ABC分割成两个等腰三角形,则这两个等腰三角形的顶角的度数分别是( )
100°、140°或100°、20° B. 100°、140°
C. 100°、20° D. 140°、20°
【变式4】直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、F.
(1)如果∠AFE=65°,求∠CDF的度数;
(2)若折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.
类型三、 动点运动的等腰三角形的分类讨论
3.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠CDE= °,∠AED= °,当点D从点B向点C运动时,∠CDE逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请求出此时∠BDA的度数;若不存在,请说明理由.
举一反三:
【变式1】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
【变式2】如图,在△ABC中,AB=AC=3,∠B=50°,点D在线段BC上运动(不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)当∠BDA=105°时,∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.
【变式3】如图所示,已知△ABC中,∠B=90°,AB=16cm,AC=20cm,P、Q是△ABC的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
根据以上信息,回答下面问题:
(1)求BC的长度;
(2)当t为何值时,点P在边AC的垂直平分线上?
(3)当点Q在边CA上运动时,是否存在t的值,使△BCQ为等腰三角形,若存在,请求出t的值;若不存在,请说明理由.
【变式4】如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,顶点C,D都在第一象限内,OA、OB的长分别为4和3.
(1)求点D的坐标;
(2)求直线BC的解析式;
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【学习目标】
1.掌握等腰三角形分类讨论的方法;
2.举一反三,利用等腰三角形的性质,理解运用在动点问题中.
【要点梳理】
等腰三角形的分类讨论
遇角需讨论:顶角和底角;
遇边需讨论:底边和腰;
遇高需讨论:形内和形外.
【典型例题】
类型一、等腰三角形的分类讨论求角或边
1.等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的腰长为( )
A.3cm B.6cm C.3cm或6cm D.3cm或9cm
举一反三:
【变式1】已知△ABC是等腰三角形,若∠A=50°,则△ABC的顶角度数是( )
A.50° B.50°或80° C.80° D.50°或65°
【变式2】已知等腰三角形一腰的垂直平分线与另一腰所在的直线的夹角为40°,则此等腰三角形的顶角是( )
A.50° B.130° C.50°或 140° D.50°或 130°
【变式3】一个等腰三角形一个内角是另一个内角的2倍,则这个三角形底角为( )
A.72°或45° B.45°或36° C.36°或45° D.72°或90°
【变式4】在等腰中,,中线将这个三角形的周长分为和的两个部分,则这个等腰三角形的底边长为( )
A. B. C.或 D.或
【变式5】等腰三角形一腰上的高与另一腰的夹角为,则该等腰三角形顶角的度数为( )
B. C. D.或
类型二、 三角形内的等腰三角形分类讨论
2.Rt△ACB中,∠C=90°,∠A=30°,在直线BC或直线AC上找到一点P,使△PAB是等腰三角形,则满足条件的点P的个数是( )
4 B.6 C.7 D.8
举一反三:
【变式1】在△ABC中∠B=20°,∠A=110°,点P在△ABC的三边上运动,当△PAC成为等腰三角形时,顶角是 .
【变式2】如图,∠MON=43°,点A在射线OM上,动点P在射线ON上滑动,要使△AOP为等腰三角形,满足条件的点P共有( )
A. 1个 B. 2个
C. 3个 D. 4个
【变式3】如图,在△ABC中,∠BAC=120°,∠B=40°,若将△ABC分割成两个等腰三角形,则这两个等腰三角形的顶角的度数分别是( )
100°、140°或100°、20° B. 100°、140°
C. 100°、20° D. 140°、20°
【变式4】直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、F.
(1)如果∠AFE=65°,求∠CDF的度数;
(2)若折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.
类型三、 动点运动的等腰三角形的分类讨论
3.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠CDE= °,∠AED= °,当点D从点B向点C运动时,∠CDE逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请求出此时∠BDA的度数;若不存在,请说明理由.
举一反三:
【变式1】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
【变式2】如图,在△ABC中,AB=AC=3,∠B=50°,点D在线段BC上运动(不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)当∠BDA=105°时,∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.
【变式3】如图所示,已知△ABC中,∠B=90°,AB=16cm,AC=20cm,P、Q是△ABC的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.
根据以上信息,回答下面问题:
(1)求BC的长度;
(2)当t为何值时,点P在边AC的垂直平分线上?
(3)当点Q在边CA上运动时,是否存在t的值,使△BCQ为等腰三角形,若存在,请求出t的值;若不存在,请说明理由.
【变式4】如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,顶点C,D都在第一象限内,OA、OB的长分别为4和3.
(1)求点D的坐标;
(2)求直线BC的解析式;
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
