数学人教A版(2019)必修第一册1.2集合间的基本关系(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册1.2集合间的基本关系(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 16:31:33 | ||
图片预览






文档简介
(共17张PPT)
1.2集合间的基本关系
第一章 集合与常用逻辑用语
1. 了解集合之间包含与相等的含义,能识别给定集合的子集;
2. 理解子集、真子集、空集的概念;
3. 能使用 Venn 图表达集合间的关系,体会数形结合的思想.
学习目标:
实数有大小关系
如:5<7,5>3
实数有相等关系 如:5=5
确定集合的研究问题:集合间的关系,集合的运算
问题 上一节我们学习了集合,对于这个新的研究对象,接下来该如何研究呢?比如要研究些什么?用什么方法研究?
集合与集合之间呢?
类比 “实数”
情景导入
回顾实数研究了哪些内容:实数间的关系、实数的运算等
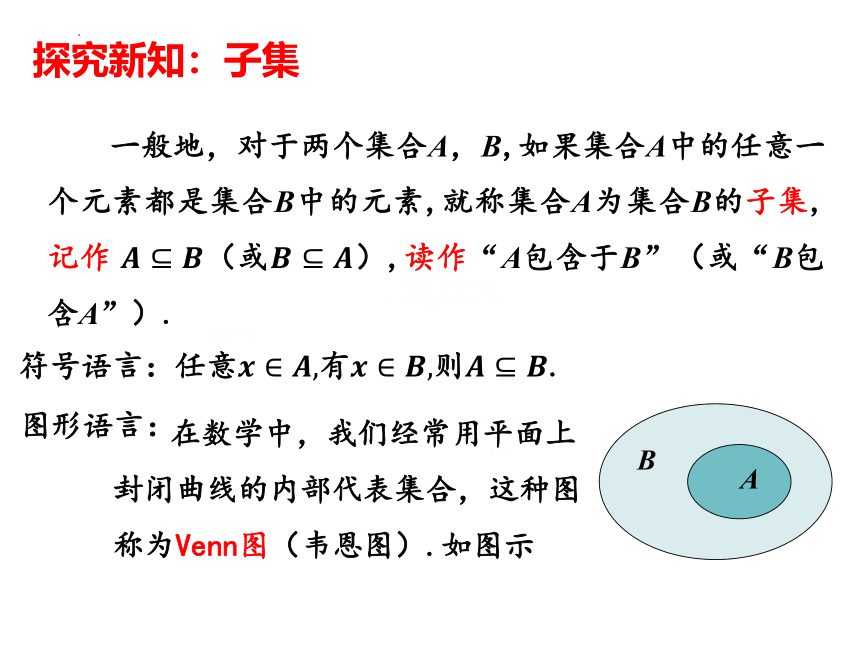
探究新知:子集
① A ={l,2,3},B ={1,2,3,4,5};
② A为滕州二中高一(2)班全体女生组成的集合, B为这个班全体学生组成的集合;
③ E={x | x是两边相等的三角形}, F={x| x是等腰三角形} .
问题:你从哪个角度来分析每组两个集合间的关系?
从元素与集合之间的关系.
思考: 观察下面的例子,类比实数间的大小或相等关系,你能发现下面两个集合之间的关系吗?
集合A小
集合B大
集合相等
Male air bring is Signs Creepiest god air fish land.
Male air bring is Signs Creepiest god.
STEP 3
STEP 2
一般地,对于两个集合A,B,如果集合A中的任意一个元素都是集合B中的元素,就称集合A为集合B的子集,记作 (或),读作“A包含于B”(或“B包含A”).
A
B
在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图称为Venn图(韦恩图).如图示
符号语言:任意有则.
探究新知:子集
图形语言:
探究新知:集合相等
③ E={x | x是两边相等的三角形}, F={x| x是等腰三角形} .
思考:集合E是集合F的子集吗?
思考:集合F是集合E的子集吗?
定义:如果集合 A 的任何一个元素都是集合 B 的元素,同时集合 B 的任何一个元素都是集合 A 的元素,那么集合 A 与集合 B 相等,记作A = B.
也就是说,若,且 ,则A = B.
A(B)
思考:你能举出几个具有包含关系、相等关系的集合吗?
思考:与实数中的结论“若a≥b,且b≥a,则a=b”相类比,你有什么体会?
典型例题
例1 判断下列各题中集合A是否为集合B的子集,并说明理由:
(1)A={1, 2, 3},B={x|x是8的约数};
(2)A={x|x是长方形},
B={x|x是两条对角线相等的平行四边形}.
解:(1) 因为3不是8的约数,所以集合A不是集合B 的子集.
(2) 因为若x是长方形,则x一定是两条对角线相等的平行四边形,所以集合A是集合B的子集.
如果集合A B,但存在元素x∈B,且x A,就称集合A是集合B的真子集,记作
A B(或B A)
读作:“A真包含于B”(或“B真包含A”)
探究新知:真子集
A
B
思考:子集和真子集的区别与联系是什么?
子集只要满足:集合A中任意一个元素都是集合B中的元素,真子集则要在子集的基础上,找到元素.
探究新知:空集
没有实数根,所以方程的实数根组成的集合中没有元素.
规定:空集是任何集合的子集
空集是任意非空集合的真子集
空集与集合{0}相等吗?二者之间是什么关系?
一般地,我们把不含任何元素的集合叫做空集,记为
思考 包含关系{a} A与属于关系a∈A有什么区别?
试结合实例作出解释?
包含关系是集合与集合之间的关系,用“ ”表示;
属于关系是元素与集合之间的关系,用“∈”表示.
二者切不可混淆,用符号之前要搞清楚是元素与集合还是集合与集合的关系.
P8练习2. 用适当的符号填空:
(1) a___{a,b,c};
(2) 0___{x|x2=0};
(3) ___{x∈R|x2+1=0};
(4) {0,1}___N;
(5) {0}___{x|x2=x};
(6) {2,1}___{x|x2-3x+2=0};
∈
∈
=
=
练习:判断下列命题的真假:
(1)任何一个集合都是它本身的子集,即A A;
(2)对于集合A, B, C,如果A B,且B C,那么A C;
C
B
A
例2 (1)分别写出下列集合的子集及其个数:
,{a},{a,b},{a,b,c}.
(2)由(1)你发现集合M中含有n个元素,则集合M有多少 个子集?
解:(1) 的子集有: ,即 有1个子集;
{a}的子集有: ,{a},即{a}有2个子集;
{a,b}的子集有: ,{a},{b},{a,b},即{a,b}有4个子集;
{a,b,c}的子集有: ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c},即{a,b,c}有8个子集.
典型例题
(2)由(1)可得:当n=0时,集合M有1=20个子集;
当n=1时,集合M有2=21个子集;
当n=2时,集合M有4=22个子集;
当n=3时,集合M有8=23个子集;
因此含有n个元素的集合M有2n个子集.
典型例题
例2 (1)分别写出下列集合的子集及其个数:
,{a},{a,b},{a,b,c}.
(2)由(1)你发现集合M中含有n个元素,则集合M有多少 个子集?
练习:课本第9页练习3
Male air bring is Signs Creepiest god air fish land.
Male air bring is Signs Creepiest god.
STEP 3
STEP 2
课堂小结
1.集合间的基本关系:子集、集合相等、真子集、空集
2.常用结论:
①空集是任何集合的子集
②任何一个集合是它本身的子集,即
③对于集合A, B, C,如果且B,那么
④对于集合A, B,如果 且则.
例1:已知集合A={-1,3,2m-1},集合B={3,m2} .
若B A,求实数m的值.
解:∵B A,
∴3∈A,m2∈A.
∴m2=-1(舍去)或m2=2m-1.
解得m=1.
∴m=1.
拓展例题
解:(1)当m+1>2m-1,即m<2时,B= ,满足B A.
当m+1≤2m-1,即m≥2时,要使B A成立,
需,可得2≤m≤3.综上所述,m≤3时有B A.
例2.集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
(1)若B A,求实数m的取值范围;
拓展例题
拓展例题
解:(2)当x∈Z时,A={-2,-1,0,1,2,3,4,5}.
∴A的非空真子集个数为:28-2=254.
例2.集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
(2)当x∈Z时,求A的非空真子集的个数;
1.2集合间的基本关系
第一章 集合与常用逻辑用语
1. 了解集合之间包含与相等的含义,能识别给定集合的子集;
2. 理解子集、真子集、空集的概念;
3. 能使用 Venn 图表达集合间的关系,体会数形结合的思想.
学习目标:
实数有大小关系
如:5<7,5>3
实数有相等关系 如:5=5
确定集合的研究问题:集合间的关系,集合的运算
问题 上一节我们学习了集合,对于这个新的研究对象,接下来该如何研究呢?比如要研究些什么?用什么方法研究?
集合与集合之间呢?
类比 “实数”
情景导入
回顾实数研究了哪些内容:实数间的关系、实数的运算等
探究新知:子集
① A ={l,2,3},B ={1,2,3,4,5};
② A为滕州二中高一(2)班全体女生组成的集合, B为这个班全体学生组成的集合;
③ E={x | x是两边相等的三角形}, F={x| x是等腰三角形} .
问题:你从哪个角度来分析每组两个集合间的关系?
从元素与集合之间的关系.
思考: 观察下面的例子,类比实数间的大小或相等关系,你能发现下面两个集合之间的关系吗?
集合A小
集合B大
集合相等
Male air bring is Signs Creepiest god air fish land.
Male air bring is Signs Creepiest god.
STEP 3
STEP 2
一般地,对于两个集合A,B,如果集合A中的任意一个元素都是集合B中的元素,就称集合A为集合B的子集,记作 (或),读作“A包含于B”(或“B包含A”).
A
B
在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图称为Venn图(韦恩图).如图示
符号语言:任意有则.
探究新知:子集
图形语言:
探究新知:集合相等
③ E={x | x是两边相等的三角形}, F={x| x是等腰三角形} .
思考:集合E是集合F的子集吗?
思考:集合F是集合E的子集吗?
定义:如果集合 A 的任何一个元素都是集合 B 的元素,同时集合 B 的任何一个元素都是集合 A 的元素,那么集合 A 与集合 B 相等,记作A = B.
也就是说,若,且 ,则A = B.
A(B)
思考:你能举出几个具有包含关系、相等关系的集合吗?
思考:与实数中的结论“若a≥b,且b≥a,则a=b”相类比,你有什么体会?
典型例题
例1 判断下列各题中集合A是否为集合B的子集,并说明理由:
(1)A={1, 2, 3},B={x|x是8的约数};
(2)A={x|x是长方形},
B={x|x是两条对角线相等的平行四边形}.
解:(1) 因为3不是8的约数,所以集合A不是集合B 的子集.
(2) 因为若x是长方形,则x一定是两条对角线相等的平行四边形,所以集合A是集合B的子集.
如果集合A B,但存在元素x∈B,且x A,就称集合A是集合B的真子集,记作
A B(或B A)
读作:“A真包含于B”(或“B真包含A”)
探究新知:真子集
A
B
思考:子集和真子集的区别与联系是什么?
子集只要满足:集合A中任意一个元素都是集合B中的元素,真子集则要在子集的基础上,找到元素.
探究新知:空集
没有实数根,所以方程的实数根组成的集合中没有元素.
规定:空集是任何集合的子集
空集是任意非空集合的真子集
空集与集合{0}相等吗?二者之间是什么关系?
一般地,我们把不含任何元素的集合叫做空集,记为
思考 包含关系{a} A与属于关系a∈A有什么区别?
试结合实例作出解释?
包含关系是集合与集合之间的关系,用“ ”表示;
属于关系是元素与集合之间的关系,用“∈”表示.
二者切不可混淆,用符号之前要搞清楚是元素与集合还是集合与集合的关系.
P8练习2. 用适当的符号填空:
(1) a___{a,b,c};
(2) 0___{x|x2=0};
(3) ___{x∈R|x2+1=0};
(4) {0,1}___N;
(5) {0}___{x|x2=x};
(6) {2,1}___{x|x2-3x+2=0};
∈
∈
=
=
练习:判断下列命题的真假:
(1)任何一个集合都是它本身的子集,即A A;
(2)对于集合A, B, C,如果A B,且B C,那么A C;
C
B
A
例2 (1)分别写出下列集合的子集及其个数:
,{a},{a,b},{a,b,c}.
(2)由(1)你发现集合M中含有n个元素,则集合M有多少 个子集?
解:(1) 的子集有: ,即 有1个子集;
{a}的子集有: ,{a},即{a}有2个子集;
{a,b}的子集有: ,{a},{b},{a,b},即{a,b}有4个子集;
{a,b,c}的子集有: ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c},即{a,b,c}有8个子集.
典型例题
(2)由(1)可得:当n=0时,集合M有1=20个子集;
当n=1时,集合M有2=21个子集;
当n=2时,集合M有4=22个子集;
当n=3时,集合M有8=23个子集;
因此含有n个元素的集合M有2n个子集.
典型例题
例2 (1)分别写出下列集合的子集及其个数:
,{a},{a,b},{a,b,c}.
(2)由(1)你发现集合M中含有n个元素,则集合M有多少 个子集?
练习:课本第9页练习3
Male air bring is Signs Creepiest god air fish land.
Male air bring is Signs Creepiest god.
STEP 3
STEP 2
课堂小结
1.集合间的基本关系:子集、集合相等、真子集、空集
2.常用结论:
①空集是任何集合的子集
②任何一个集合是它本身的子集,即
③对于集合A, B, C,如果且B,那么
④对于集合A, B,如果 且则.
例1:已知集合A={-1,3,2m-1},集合B={3,m2} .
若B A,求实数m的值.
解:∵B A,
∴3∈A,m2∈A.
∴m2=-1(舍去)或m2=2m-1.
解得m=1.
∴m=1.
拓展例题
解:(1)当m+1>2m-1,即m<2时,B= ,满足B A.
当m+1≤2m-1,即m≥2时,要使B A成立,
需,可得2≤m≤3.综上所述,m≤3时有B A.
例2.集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
(1)若B A,求实数m的取值范围;
拓展例题
拓展例题
解:(2)当x∈Z时,A={-2,-1,0,1,2,3,4,5}.
∴A的非空真子集个数为:28-2=254.
例2.集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
(2)当x∈Z时,求A的非空真子集的个数;
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
