人教版数学九年级下册28.1.2余弦和正切 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级下册28.1.2余弦和正切 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 18:19:12 | ||
图片预览



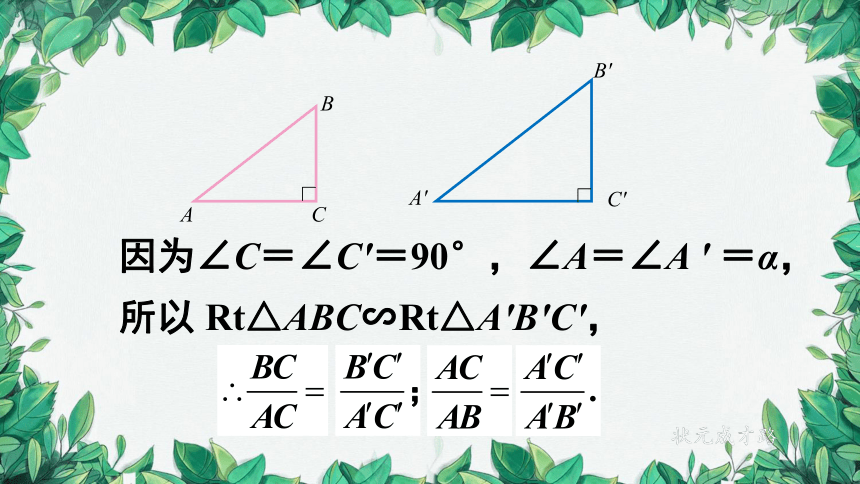


文档简介
(共23张PPT)
余弦和正切
我们是如何得到锐角正弦的概念的?
sin A= = .
∠A 的对边
斜边
温故知新
复习导入
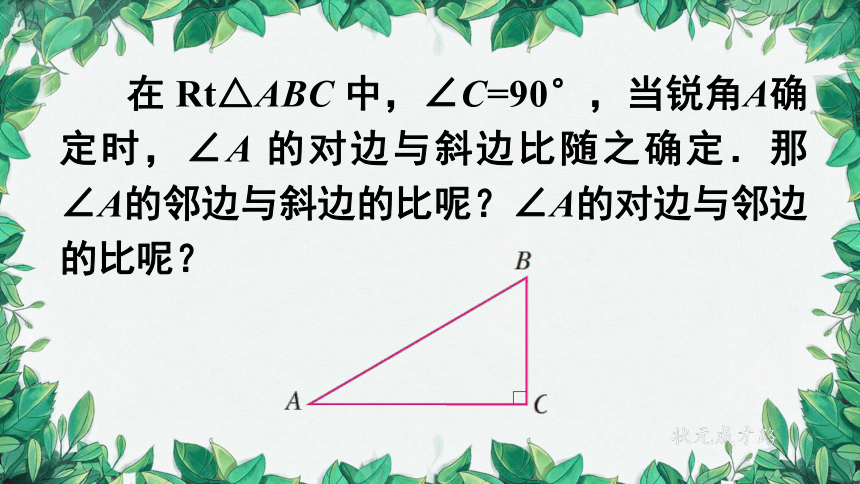
在 Rt△ABC 中,∠C=90°,当锐角A确定时,∠A 的对边与斜边比随之确定.那∠A的邻边与斜边的比呢?∠A的对边与邻边的比呢?
余弦、正切的定义
知识点1
探究 在Rt△ABC中,当锐角A确定时,∠A的对边与斜边的比随之确定.那∠A的邻边与斜边的比呢?∠A的对边与邻边的比呢?
猜想
∠A邻边与斜边的比、对边与邻边的比都是定值.
推进新课
探究
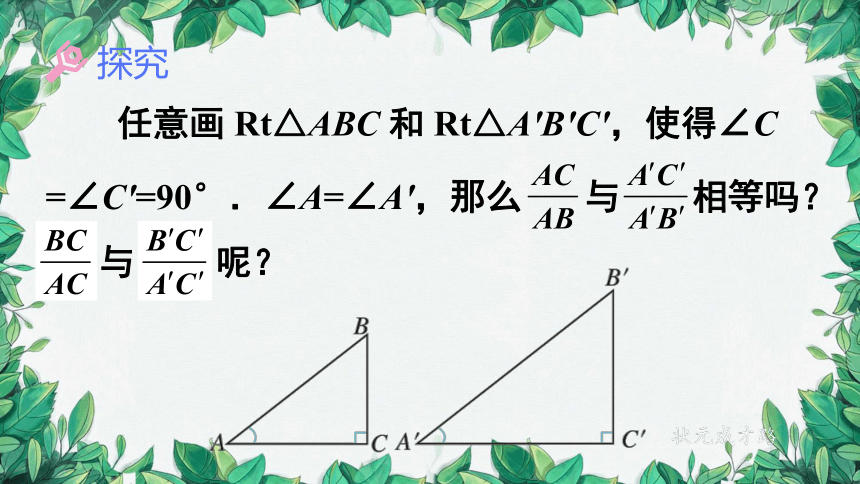
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C
=∠C'=90°.∠A=∠A',那么 与 相等吗?
与 呢?
A'
B'
C'
因为∠C=∠C′=90°,∠A=∠A ′ =α,
A
B
C
所以 Rt△ABC∽Rt△A'B'C',
在 Rt△ABC 中,当锐角 A 的度数一定时,∠A 的邻边与斜边的比、对边与邻边的比都是一个固定值.
∠A的对边与邻边的比,记作tanA.
∠A的邻边与斜边的比,记作cosA.
余弦
正切
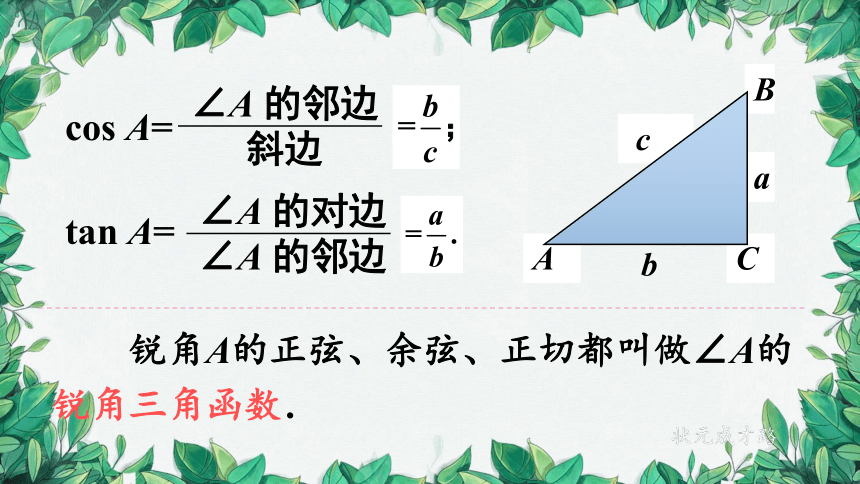
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
a
C
A
c
B
b
cos A=
∠A 的邻边
斜边
tan A=
∠A 的对边
∠A 的邻边
1.如图,在Rt△ABC中,∠C=90°,BC=6,
sinA= ,求cosA、tanB的值.
A
B
C
6
解:∵
∴
练 习
又
A
B
C
6
运用正弦、余弦定义求值
知识点2
tanA= = .
cosA= = ;
解:在 Rt△ABC 中,AC= =8.
sinA= = ;
6
C
A
10
B
例 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求 sinA,cosA,tanA 的值.
思考
若条件不变,你能求出sinB,cosB,tanB的值吗?
6
C
A
10
B
8
tanB= = .
cosB= = ;
sinB= = ;
观察前面的结果,你有什么发现?
小结
若∠A +∠ B = 90°,
则sinA = cosB,tanA·tanB=1.
sinA= = ;
cosB= = ;
tanA= = .
tanB= = .
练习
2.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:由勾股定理
A
B
C
13
12
(1)
A
B
C
3
2
(2)
A
B
C
3
2
(2)
解:由勾股定理
3.在Rt△ABC中,∠C=90°,如果各边长都扩大到原来的2倍,那么∠A的正弦值、余弦值和正切值有什么变化?
答:∠A的正弦、余弦和正切值没有变化.
理由:锐角三角函数值与三角形大小无关.
1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则下列等式中不正确的是( )
A.a=c×sinA B.b=a×tanB
C.b=c×sinB D.
D
基础巩固
随堂演练
2.如图,将∠AOB放置在5×5的正方形网格中,则cos∠AOB的值是( )
C
A. B.
C. D.
A
O
B
综合应用
3.如图,在等腰△ABC中,AB=AC=5,BC=6.求sinB,cosB,tanB的值.
解:作AD⊥BC于D.
∵AB=AC=5,∴BD=DC= BC=3.
∴在Rt△ABD中,AD=
∴sinB=
a
C
A
c
B
b
余弦
正切
cos A=
∠A 的邻边
斜边
tan A=
∠A 的对边
∠A 的邻边
课堂小结
拓展延伸
在Rt△ABC中,∠C=90°,请利用锐角三角函数的定义及勾股定理探索∠A的正弦、余弦之间的关系.
解:∠A的正弦、余弦值的平方和等于1.
理由如下:
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
余弦和正切
我们是如何得到锐角正弦的概念的?
sin A= = .
∠A 的对边
斜边
温故知新
复习导入
在 Rt△ABC 中,∠C=90°,当锐角A确定时,∠A 的对边与斜边比随之确定.那∠A的邻边与斜边的比呢?∠A的对边与邻边的比呢?
余弦、正切的定义
知识点1
探究 在Rt△ABC中,当锐角A确定时,∠A的对边与斜边的比随之确定.那∠A的邻边与斜边的比呢?∠A的对边与邻边的比呢?
猜想
∠A邻边与斜边的比、对边与邻边的比都是定值.
推进新课
探究
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C
=∠C'=90°.∠A=∠A',那么 与 相等吗?
与 呢?
A'
B'
C'
因为∠C=∠C′=90°,∠A=∠A ′ =α,
A
B
C
所以 Rt△ABC∽Rt△A'B'C',
在 Rt△ABC 中,当锐角 A 的度数一定时,∠A 的邻边与斜边的比、对边与邻边的比都是一个固定值.
∠A的对边与邻边的比,记作tanA.
∠A的邻边与斜边的比,记作cosA.
余弦
正切
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
a
C
A
c
B
b
cos A=
∠A 的邻边
斜边
tan A=
∠A 的对边
∠A 的邻边
1.如图,在Rt△ABC中,∠C=90°,BC=6,
sinA= ,求cosA、tanB的值.
A
B
C
6
解:∵
∴
练 习
又
A
B
C
6
运用正弦、余弦定义求值
知识点2
tanA= = .
cosA= = ;
解:在 Rt△ABC 中,AC= =8.
sinA= = ;
6
C
A
10
B
例 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求 sinA,cosA,tanA 的值.
思考
若条件不变,你能求出sinB,cosB,tanB的值吗?
6
C
A
10
B
8
tanB= = .
cosB= = ;
sinB= = ;
观察前面的结果,你有什么发现?
小结
若∠A +∠ B = 90°,
则sinA = cosB,tanA·tanB=1.
sinA= = ;
cosB= = ;
tanA= = .
tanB= = .
练习
2.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:由勾股定理
A
B
C
13
12
(1)
A
B
C
3
2
(2)
A
B
C
3
2
(2)
解:由勾股定理
3.在Rt△ABC中,∠C=90°,如果各边长都扩大到原来的2倍,那么∠A的正弦值、余弦值和正切值有什么变化?
答:∠A的正弦、余弦和正切值没有变化.
理由:锐角三角函数值与三角形大小无关.
1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则下列等式中不正确的是( )
A.a=c×sinA B.b=a×tanB
C.b=c×sinB D.
D
基础巩固
随堂演练
2.如图,将∠AOB放置在5×5的正方形网格中,则cos∠AOB的值是( )
C
A. B.
C. D.
A
O
B
综合应用
3.如图,在等腰△ABC中,AB=AC=5,BC=6.求sinB,cosB,tanB的值.
解:作AD⊥BC于D.
∵AB=AC=5,∴BD=DC= BC=3.
∴在Rt△ABD中,AD=
∴sinB=
a
C
A
c
B
b
余弦
正切
cos A=
∠A 的邻边
斜边
tan A=
∠A 的对边
∠A 的邻边
课堂小结
拓展延伸
在Rt△ABC中,∠C=90°,请利用锐角三角函数的定义及勾股定理探索∠A的正弦、余弦之间的关系.
解:∠A的正弦、余弦值的平方和等于1.
理由如下:
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
