1.2 怎样判定三角形相似(4) 课件(共14张PPT)
文档属性
| 名称 | 1.2 怎样判定三角形相似(4) 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 12:58:27 | ||
图片预览



文档简介
(共14张PPT)
1.2 怎样判定三角形相似(4)
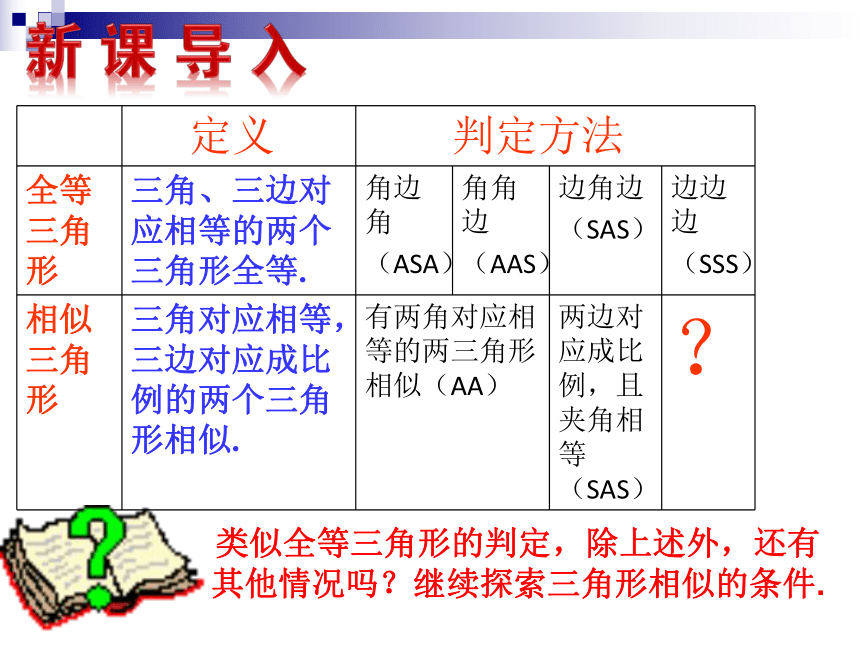
定义 判定方法 全等三角形 三角、三边对应相等的两个三角形全等. 角边角 (ASA) 角角边 (AAS) 边角边 (SAS) 边边边
(SSS)
相似三角形 三角对应相等,三边对应成比例的两个三角形相似. 有两角对应相等的两三角形相似(AA) 两边对应成比例,且夹角相等(SAS) ?
类似全等三角形的判定,除上述外,还有其他情况吗?继续探索三角形相似的条件.
1.了解三边成比例的两个三角形相似判定定理的证明过程.
2.能运用相似三角形的判定定理证明三角形相似.
3.经历类比、猜想、探究、归纳、应用等数学活动,提高学生分析问题、解决问题的能力.
4.通过应用相似三角形的判定方法和性质解决简单问题,培养学生的应用意识.
学习目标
重点:能运用三边成比例的两个三角形相似证明三角形相似.
难点:相似三角形判定定理的证明过程.
教学重难点
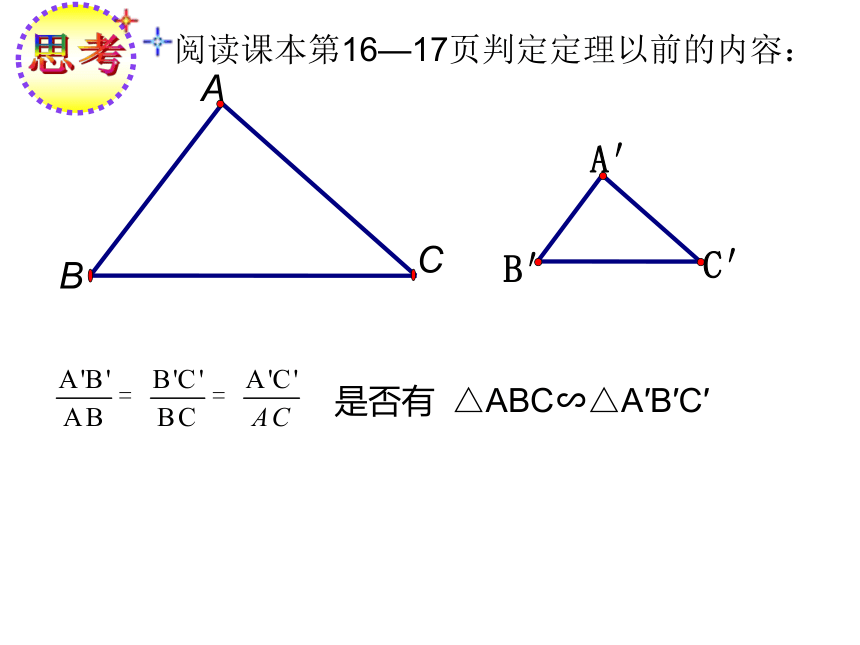
思考
是否有
A
B
C
阅读课本第16—17页判定定理以前的内容:
A′
B′
C′
△ABC∽△A′B′C′
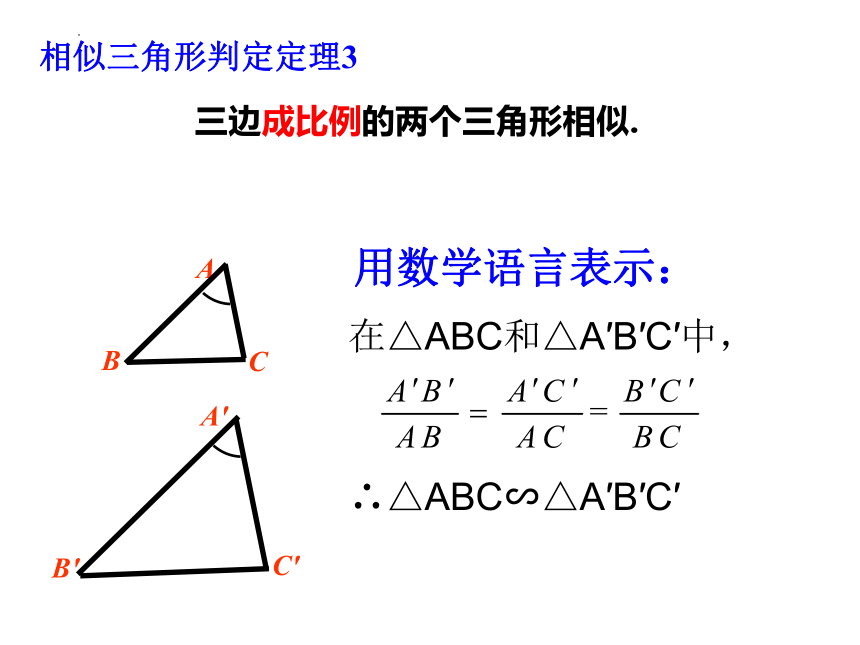
三边成比例的两个三角形相似.
A
B
C
A′
B′
C′
相似三角形判定定理3
在△ABC和△A′B′C′中,
∴△ABC∽△A′B′C′
用数学语言表示:
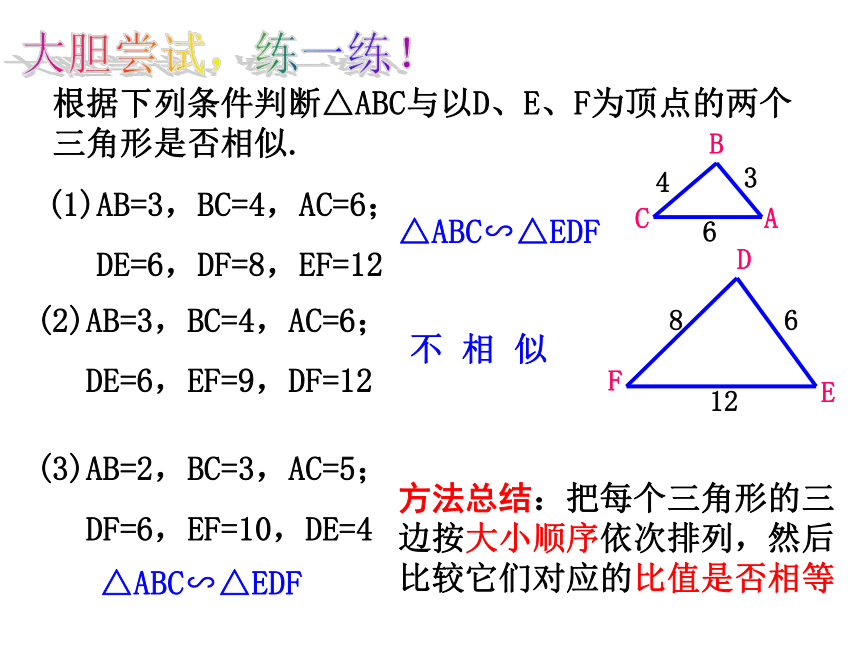
根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似.
(1)AB=3,BC=4,AC=6;
DE=6,DF=8,EF=12
(2)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12
△ABC∽△EDF
不 相 似
A
B
C
E
D
F
3
4
6
6
8
12
大胆尝试,练一练!
方法总结:把每个三角形的三边按大小顺序依次排列,然后比较它们对应的比值是否相等
(3)AB=2,BC=3,AC=5;
DF=6,EF=10,DE=4
△ABC∽△EDF
例1:如图,已知 .不另外添加字母,写出 图中相等的角,并说明理由.
解:在ΔABC 和ΔADE 中,
∴ ΔABC∽ΔADE .
∴∠BAC =∠DAE , ∠B =∠D , ∠C = ∠E .
A
C
B
D
E
由∠BAC =∠DAE还可以推出∠BAD =∠CAE.
变式训练:同步第10页5题(1)(2)
挑战自我
(1)如果两个三角形的三条边的比都是3:4:5,这两个三角形相似吗?
(2)在什么条件下两个等腰三角形相似?在什么条件下两个直角三角形相似?
判定三角形相似的方法
定义
判定定理1
判定定理2
判定定理3
小结
作业:
课本第21页
习题1.2第7题
1、根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由
AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=24cm.
解:∵
∴
达标检测:
(三边对应成比例,两三角形相似)
∽
∴
A
B
C
D
E
F
2.如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC∽△DEF.
5
12
8
10
16
24
A
B
C
变式训练: 如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC和△DEF相似.
5
12
8
D
E
F
D
F
E
10
10
D
E
F
10
1.2 怎样判定三角形相似(4)
定义 判定方法 全等三角形 三角、三边对应相等的两个三角形全等. 角边角 (ASA) 角角边 (AAS) 边角边 (SAS) 边边边
(SSS)
相似三角形 三角对应相等,三边对应成比例的两个三角形相似. 有两角对应相等的两三角形相似(AA) 两边对应成比例,且夹角相等(SAS) ?
类似全等三角形的判定,除上述外,还有其他情况吗?继续探索三角形相似的条件.
1.了解三边成比例的两个三角形相似判定定理的证明过程.
2.能运用相似三角形的判定定理证明三角形相似.
3.经历类比、猜想、探究、归纳、应用等数学活动,提高学生分析问题、解决问题的能力.
4.通过应用相似三角形的判定方法和性质解决简单问题,培养学生的应用意识.
学习目标
重点:能运用三边成比例的两个三角形相似证明三角形相似.
难点:相似三角形判定定理的证明过程.
教学重难点
思考
是否有
A
B
C
阅读课本第16—17页判定定理以前的内容:
A′
B′
C′
△ABC∽△A′B′C′
三边成比例的两个三角形相似.
A
B
C
A′
B′
C′
相似三角形判定定理3
在△ABC和△A′B′C′中,
∴△ABC∽△A′B′C′
用数学语言表示:
根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似.
(1)AB=3,BC=4,AC=6;
DE=6,DF=8,EF=12
(2)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12
△ABC∽△EDF
不 相 似
A
B
C
E
D
F
3
4
6
6
8
12
大胆尝试,练一练!
方法总结:把每个三角形的三边按大小顺序依次排列,然后比较它们对应的比值是否相等
(3)AB=2,BC=3,AC=5;
DF=6,EF=10,DE=4
△ABC∽△EDF
例1:如图,已知 .不另外添加字母,写出 图中相等的角,并说明理由.
解:在ΔABC 和ΔADE 中,
∴ ΔABC∽ΔADE .
∴∠BAC =∠DAE , ∠B =∠D , ∠C = ∠E .
A
C
B
D
E
由∠BAC =∠DAE还可以推出∠BAD =∠CAE.
变式训练:同步第10页5题(1)(2)
挑战自我
(1)如果两个三角形的三条边的比都是3:4:5,这两个三角形相似吗?
(2)在什么条件下两个等腰三角形相似?在什么条件下两个直角三角形相似?
判定三角形相似的方法
定义
判定定理1
判定定理2
判定定理3
小结
作业:
课本第21页
习题1.2第7题
1、根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由
AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=24cm.
解:∵
∴
达标检测:
(三边对应成比例,两三角形相似)
∽
∴
A
B
C
D
E
F
2.如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC∽△DEF.
5
12
8
10
16
24
A
B
C
变式训练: 如图,已知△ABC与△DEF中,AB=5,BC=12,AC=8, DE=10,则当DF=____,EF=____时,△ABC和△DEF相似.
5
12
8
D
E
F
D
F
E
10
10
D
E
F
10
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
