1.3 相似三角形的性质(1) 课件(共14张PPT)
文档属性
| 名称 | 1.3 相似三角形的性质(1) 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 339.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 13:01:58 | ||
图片预览






文档简介
(共14张PPT)
第1章 图形的相似
1.3 相似三角形的性质
新课导入
全等三角形的对应线段(对应边上的高、对应边上的中线、对应角的平分线)相等、面积相等.
那么,相似三角形的对应线段具有什么性质呢?相似三角形的面积具有什么性质呢?
你还记得全等三角形的对应线段、面积具有什么性质吗?
新课探究
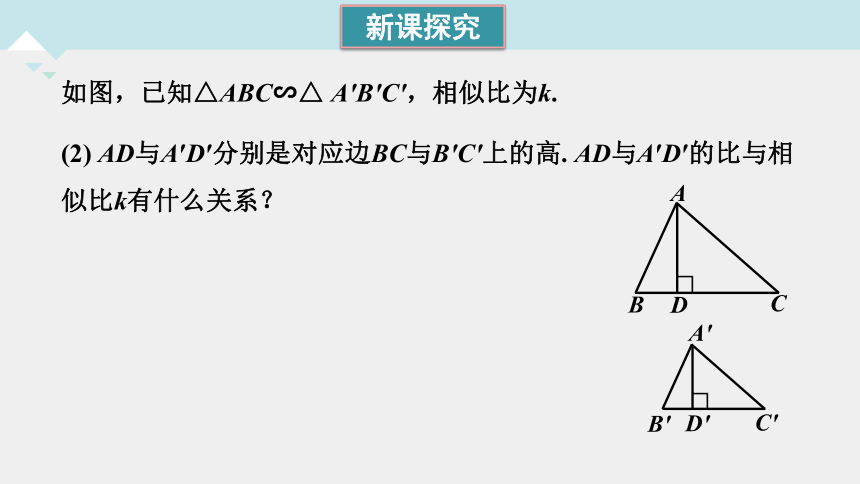
如图,已知△ABC∽△ A′B′C′,相似比为k.
A′
B′
C′
D′
A
B
C
D
(1) AD与A′D′分别是对应边BC与B′C′上的高.除△ABC∽△A′B′C′外,图中还有哪些相似三角形?为什么?
如图,已知△ABC∽△ A′B′C′,相似比为k.
(2) AD与A′D′分别是对应边BC与B′C′上的高. AD与A′D′的比与相似比k有什么关系?
新课探究
A′
B′
C′
D′
A
B
C
D
如图,已知△ABC∽△ A′B′C′,相似比为k.
(3) 若AE与A′E′分别是∠A与∠A′的平分线,则的值是多少?
新课探究
解:∵ △ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC =∠B′A′C′.
∵ AE, A′E′分别是∠BAC, ∠B′A′C′的平分线,
∴∠BAE=∠BAC =∠B′A′C′=∠B′A′E′.
∴△AEB∽△A′E′B′.
∴ =k.
A
B
C
A′
B′
C′
E′
E
如图,已知△ABC∽△ A′B′C′,相似比为k.
(4) 若AF与A′F′分别是BC与B′C′边的中线,则的值是多少?
新课探究
A
B
C
F
A′
B′
C′
F′
解:∵ △ABC∽△A′B′C′,
∴ ∠B=∠B′,==k.
又∵ ===k.
∴ △AFB∽△A′F′B′.
∴ =k.
新课探究
如图,已知△ABC∽△ A′B′C′,相似比为k.
(5)△ABC与△A′B′C′的面积之比与k有什么关系?
解:分别作△ABC与△A′B′C′的高AD,A′D′.
根据(2)的结论,知 =k.
A′
B′
C′
D′
A
B
C
D
∴= =·=k2.
∴△ABC与△A′B′C′的面积之比为k2.
新课探究
综合上面的探究结果,总结相似三角形的性质
定理 相似三角形对应线段的比都等于_________.面积的比等于_____________.
相似比
相似比的平方
注意:(1)性质定理中的对应线段是指对应边上的高、中线及对应角的平分线.
(2)相似比是有顺序的,不能颠倒两个相似三角形的顺序.
思考:两个相似四边形的面积比等于相似比的平方吗?
两个相似五边形呢?
两个相似n边形呢?
提示:多边形通过连接角的顶点分解为多个三角形,利用相似三角形的性质可得相似多边形的面积比等于相似比的平方.
新课探究
【例1】如图,在△ABC中,DE∥BC,AD∶DB=3∶1,△ABC的面积为48.求△ADE的面积.
例题讲解
A
B
C
D
E
【例2】如图,有一块锐角三角形余料ABC,它的边BC=12cm,高AD=8cm.现要用它裁出一个正方形工件,使正方形的一边在BC上,其余的两个顶点分别在AB,AC上,求裁出的正方形工件的边长.
例题讲解
A
B
C
D
P
Q
M
N
E
随堂练习
1.两个相似三角形对应角平分线的比是1∶4,它们对应高的比是______, 面积的比是_______ .
解析:小三角形与大三角形的相似比为:4∶12=1∶3,
则较小三角形的面积为:45×=5 (cm2).
1∶4
1∶16
2.两个相似三角形对应的中线长分别是4cm和12cm,若较大三角形的面积是45 cm2,则较小三角形的面积为_____ cm2.
5
随堂练习
3.两个相似三角形的一组对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短角平分线的长为x cm,则较长角平分线的长为(42-x)cm.
根据题意,得 = ,
经检验 x=18 是方程的解.
所以 42-x=42-18=24.
所以这两条角平分线的长分别为18 cm,24 cm.
解得 x=18.
课堂小结
相似三角形的性质定理
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于_________.
相似比
面积比等于______________.
相似比的平方
相似多边形的面积比等于______________.
相似比的平方
第1章 图形的相似
1.3 相似三角形的性质
新课导入
全等三角形的对应线段(对应边上的高、对应边上的中线、对应角的平分线)相等、面积相等.
那么,相似三角形的对应线段具有什么性质呢?相似三角形的面积具有什么性质呢?
你还记得全等三角形的对应线段、面积具有什么性质吗?
新课探究
如图,已知△ABC∽△ A′B′C′,相似比为k.
A′
B′
C′
D′
A
B
C
D
(1) AD与A′D′分别是对应边BC与B′C′上的高.除△ABC∽△A′B′C′外,图中还有哪些相似三角形?为什么?
如图,已知△ABC∽△ A′B′C′,相似比为k.
(2) AD与A′D′分别是对应边BC与B′C′上的高. AD与A′D′的比与相似比k有什么关系?
新课探究
A′
B′
C′
D′
A
B
C
D
如图,已知△ABC∽△ A′B′C′,相似比为k.
(3) 若AE与A′E′分别是∠A与∠A′的平分线,则的值是多少?
新课探究
解:∵ △ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC =∠B′A′C′.
∵ AE, A′E′分别是∠BAC, ∠B′A′C′的平分线,
∴∠BAE=∠BAC =∠B′A′C′=∠B′A′E′.
∴△AEB∽△A′E′B′.
∴ =k.
A
B
C
A′
B′
C′
E′
E
如图,已知△ABC∽△ A′B′C′,相似比为k.
(4) 若AF与A′F′分别是BC与B′C′边的中线,则的值是多少?
新课探究
A
B
C
F
A′
B′
C′
F′
解:∵ △ABC∽△A′B′C′,
∴ ∠B=∠B′,==k.
又∵ ===k.
∴ △AFB∽△A′F′B′.
∴ =k.
新课探究
如图,已知△ABC∽△ A′B′C′,相似比为k.
(5)△ABC与△A′B′C′的面积之比与k有什么关系?
解:分别作△ABC与△A′B′C′的高AD,A′D′.
根据(2)的结论,知 =k.
A′
B′
C′
D′
A
B
C
D
∴= =·=k2.
∴△ABC与△A′B′C′的面积之比为k2.
新课探究
综合上面的探究结果,总结相似三角形的性质
定理 相似三角形对应线段的比都等于_________.面积的比等于_____________.
相似比
相似比的平方
注意:(1)性质定理中的对应线段是指对应边上的高、中线及对应角的平分线.
(2)相似比是有顺序的,不能颠倒两个相似三角形的顺序.
思考:两个相似四边形的面积比等于相似比的平方吗?
两个相似五边形呢?
两个相似n边形呢?
提示:多边形通过连接角的顶点分解为多个三角形,利用相似三角形的性质可得相似多边形的面积比等于相似比的平方.
新课探究
【例1】如图,在△ABC中,DE∥BC,AD∶DB=3∶1,△ABC的面积为48.求△ADE的面积.
例题讲解
A
B
C
D
E
【例2】如图,有一块锐角三角形余料ABC,它的边BC=12cm,高AD=8cm.现要用它裁出一个正方形工件,使正方形的一边在BC上,其余的两个顶点分别在AB,AC上,求裁出的正方形工件的边长.
例题讲解
A
B
C
D
P
Q
M
N
E
随堂练习
1.两个相似三角形对应角平分线的比是1∶4,它们对应高的比是______, 面积的比是_______ .
解析:小三角形与大三角形的相似比为:4∶12=1∶3,
则较小三角形的面积为:45×=5 (cm2).
1∶4
1∶16
2.两个相似三角形对应的中线长分别是4cm和12cm,若较大三角形的面积是45 cm2,则较小三角形的面积为_____ cm2.
5
随堂练习
3.两个相似三角形的一组对应边的长分别是6cm和8cm,如果它们对应的两条角平分线的和为42cm,那么这两条角平分线的长分别是多少?
解:设较短角平分线的长为x cm,则较长角平分线的长为(42-x)cm.
根据题意,得 = ,
经检验 x=18 是方程的解.
所以 42-x=42-18=24.
所以这两条角平分线的长分别为18 cm,24 cm.
解得 x=18.
课堂小结
相似三角形的性质定理
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于_________.
相似比
面积比等于______________.
相似比的平方
相似多边形的面积比等于______________.
相似比的平方
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
