1.4.2 位似图形与坐标(1) 课件(共19张PPT)
文档属性
| 名称 | 1.4.2 位似图形与坐标(1) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 669.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-23 13:05:41 | ||
图片预览



文档简介
(共19张PPT)
第1章 图形的相似
1.4 图形的位似
第2课时 位似图形与坐标
学习目标
在直角坐标系中,探索并了解一个多边形的顶点坐标
(有一个顶点为原点,有一条边在横坐标轴上)分别
扩大或缩小相同倍数时,所对应的图形与原图形是
位似的.
复习导入
你还记得位似作图的一般步骤吗?
1.确定位似中心;
2.确定关键点(一般是多边形的顶点);
3.找出新图形的关键点;
4.顺次连接各点,得到所求作的图形.
利用直角坐标系可以作出符合要求的位似图形吗?
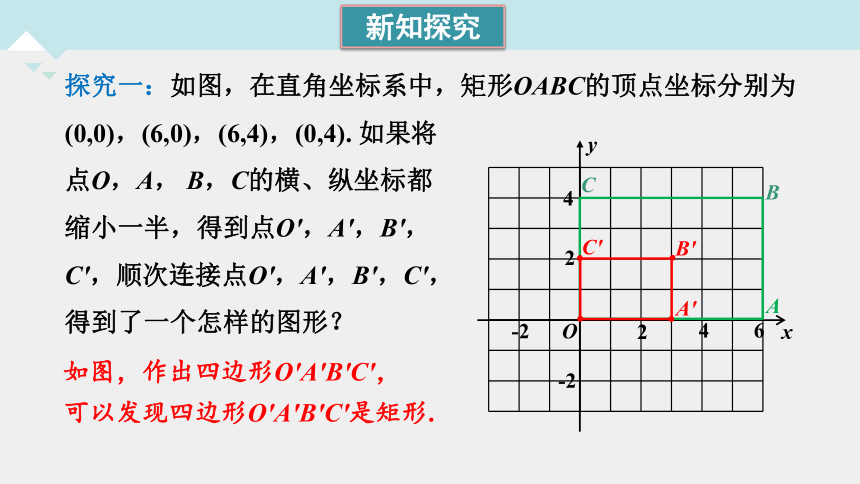
探究一:如图,在直角坐标系中,矩形OABC的顶点坐标分别为(0,0),(6,0),(6,4),(0,4). 如果将
点O,A, B,C的横、纵坐标都
缩小一半,得到点O′,A′,B′,
C′,顺次连接点O′,A′,B′,C′,
得到了一个怎样的图形?
新知探究
x
y
O
2
4
-2
2
4
-2
A
B
A'
B'
6
C
C'
如图,作出四边形O′A′B′C′,
可以发现四边形O′A′B′C′是矩形.
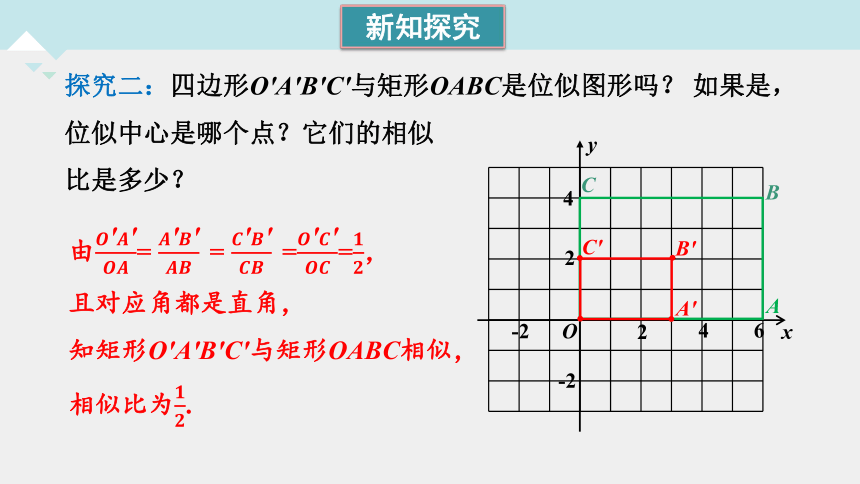
探究二:四边形O′A′B′C′与矩形OABC是位似图形吗? 如果是,位似中心是哪个点?它们的相似
比是多少?
新知探究
x
y
O
2
4
-2
2
4
-2
A
B
A'
B'
6
C
C'
由= = ==,
且对应角都是直角,
知矩形O′A′B′C′与矩形OABC相似,
相似比为.
x
y
O
2
4
-2
2
4
-2
A
B
A'
B'
6
C
C'
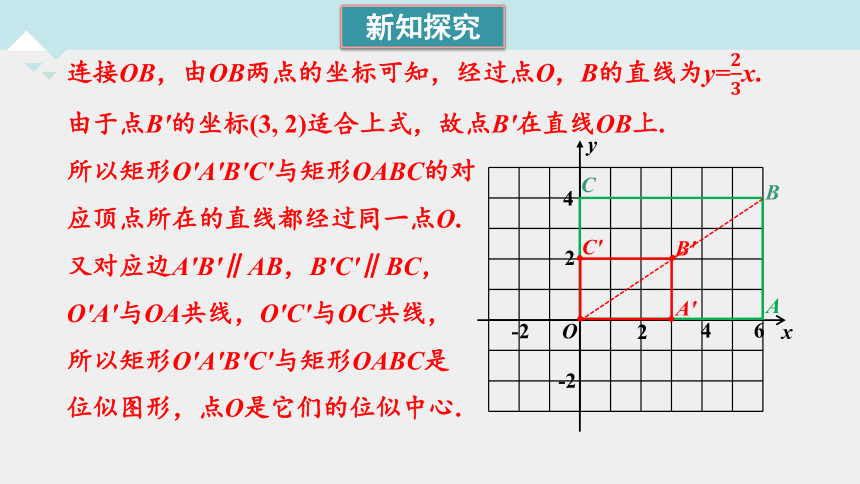
连接OB,由OB两点的坐标可知,经过点O,B的直线为y=x.
由于点B′的坐标(3, 2)适合上式,故点B′在直线OB上.
所以矩形O′A′B′C′与矩形OABC的对
应顶点所在的直线都经过同一点O.
又对应边A′B′∥AB,B′C′∥BC,
O′A′与OA共线,O′C′与OC共线,
所以矩形O′A′B′C′与矩形OABC是
位似图形,点O是它们的位似中心.
新知探究
新知探究
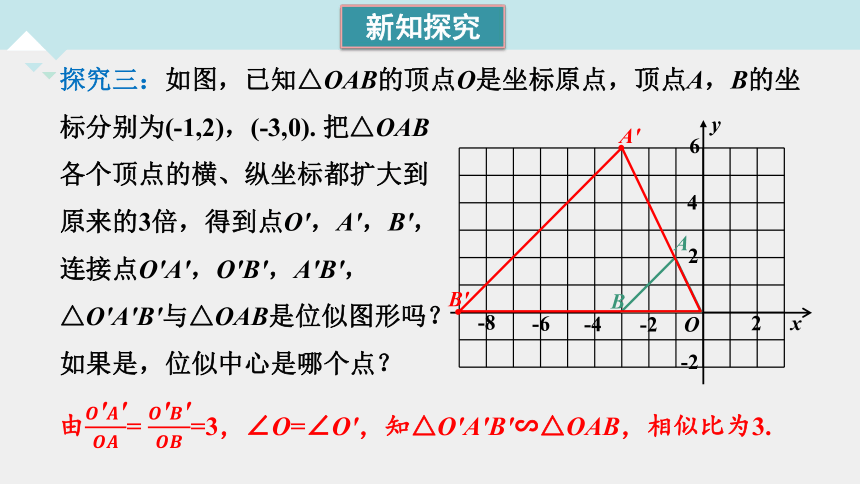
探究三:如图,已知△OAB的顶点O是坐标原点,顶点A,B的坐标分别为(-1,2),(-3,0). 把△OAB
各个顶点的横、纵坐标都扩大到
原来的3倍,得到点O′,A′,B′,
连接点O′A′,O′B′,A′B′,
△O′A′B′与△OAB是位似图形吗?
如果是,位似中心是哪个点?
x
y
O
2
-2
2
-2
A
B
6
-4
-6
A'
B'
4
-8
由= =3,∠O=∠O′,知△O′A′B′∽△OAB,相似比为3.
由OA两点的坐标可知,经过点O,A的直线为y=-2x.
由于点A′的坐标(-3, 6)适合上式,
故点A′在直线OA上.
所以△O′A′B′与△OAB的对应
顶点所在的直线都经过同一点O.
又对应边A′B′∥AB,O′A′与OA
共线,O′B′与OB共线,
所以△O′A′B′与△OAB是位似图形,点O是它们的位似中心.
x
y
O
2
-2
2
-2
A
B
6
-4
-6
A'
B'
4
-8
新知探究
新知探究
探究四:由探究一、二、三你能得出什么结论?
如果多边形有一个顶点在坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
上面得到的结论还能推广吗?如果能,说明你推广后的结论.
提示:要将上述结论推广,可适当降低命题的条件(如去掉“有一个顶点在坐标原点”的条件,再去掉“有一条边在x轴上”的条件).通过举例,画出图形,讨论上面的结论是否依然成立.
新知探究
x
y
O
2
4
-2
2
4
-2
-4
A
B
6
-6
6
如图, 在平面直角坐标系中, 四边形ABCD的顶点坐标分别为A(2,1), B(4,3), C(3,5), D(-1,3),将点A, B, C, D的横坐标、纵坐标都乘,分别得到A′ , B′ , C′ , D′ ,四边形A′B′C′D′与四边形ABCD位似吗?
如果位似,指出位似中心和相似比.
C
D
新知探究
x
y
O
2
4
-2
2
4
-2
-4
A
B
6
-6
6
C
D
坐标都乘后,得新四边形的四个顶点的坐标分别是___________________.
如图,四边形A′B′C′D′的边长为四边形ABCD的边长的___,对应点的连线都过点___.且对应边______.
(1,), (2,), (,), (-,)
O
A'
C'
B'
D'
所以四边形A′B′C′D′与四边形ABCD位似,位似中心为点O, 相似比为.
新知探究
平行
新知探究
所以,上面得到的结论还能推广,推广后的结论如下:
在平面直角坐标系中,将一个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
此结论可以称为位似图形与坐标的性质.
例题讲解
【例1】如图, 四边形OABC的顶点坐标分别为 (0,0),(2,0),(4,4),(-2,2).
(1)如果四边形O′A′B′C′与四边形OABC位似,位似中心是原点,其面积等于四边形OABC面积的倍,分别写出点A′,B′,C′的坐标.
x
y
O
2
4
-2
-4
2
4
-2
-4
A
C
B
-6
6
6
(2)画出四边形O′A′B′C′.
解:(1)由四边形O′A′B′C′与四边形OABC的面积比为,所以它们的相似比为.
将点A,B,C的坐标分别扩大到
原来的,得到A′(3,0),B′(6,6),
C′(-3,3).
(2)顺次连接O′,A′,B′,C′ ,
四边形O′A′B′C′就是要画的四边形.
例题讲解
x
y
O
2
4
-2
-4
2
4
-2
-4
A
C
B
-6
6
6
A'
C'
B'
随堂练习
1.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4) B.(-1,-2)
C. (-2,-4) D.(-2,-1)
C
随堂练习
2.如图,已知,.
(1)作出与关于轴对称的,
并写出的坐标.
(2)以原点为位似中心,在原点的另一
侧,画出,使与
位似,且.
-8 -6 -4 -2 2 4
2
-2
-4
解:
(1)
作出如图.
(2)
,
即,
画出如图.
同理,得,
-8 -6 -4 -2 2 4
2
-2
-4
-6
课堂小结
位似图形与坐标
性质
在坐标系中画位似图
在平面直角坐标系中,将一个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
首先把原图形的各点的横、纵坐标都乘相似比k或乘-k,然后描点连线即可.
第1章 图形的相似
1.4 图形的位似
第2课时 位似图形与坐标
学习目标
在直角坐标系中,探索并了解一个多边形的顶点坐标
(有一个顶点为原点,有一条边在横坐标轴上)分别
扩大或缩小相同倍数时,所对应的图形与原图形是
位似的.
复习导入
你还记得位似作图的一般步骤吗?
1.确定位似中心;
2.确定关键点(一般是多边形的顶点);
3.找出新图形的关键点;
4.顺次连接各点,得到所求作的图形.
利用直角坐标系可以作出符合要求的位似图形吗?
探究一:如图,在直角坐标系中,矩形OABC的顶点坐标分别为(0,0),(6,0),(6,4),(0,4). 如果将
点O,A, B,C的横、纵坐标都
缩小一半,得到点O′,A′,B′,
C′,顺次连接点O′,A′,B′,C′,
得到了一个怎样的图形?
新知探究
x
y
O
2
4
-2
2
4
-2
A
B
A'
B'
6
C
C'
如图,作出四边形O′A′B′C′,
可以发现四边形O′A′B′C′是矩形.
探究二:四边形O′A′B′C′与矩形OABC是位似图形吗? 如果是,位似中心是哪个点?它们的相似
比是多少?
新知探究
x
y
O
2
4
-2
2
4
-2
A
B
A'
B'
6
C
C'
由= = ==,
且对应角都是直角,
知矩形O′A′B′C′与矩形OABC相似,
相似比为.
x
y
O
2
4
-2
2
4
-2
A
B
A'
B'
6
C
C'
连接OB,由OB两点的坐标可知,经过点O,B的直线为y=x.
由于点B′的坐标(3, 2)适合上式,故点B′在直线OB上.
所以矩形O′A′B′C′与矩形OABC的对
应顶点所在的直线都经过同一点O.
又对应边A′B′∥AB,B′C′∥BC,
O′A′与OA共线,O′C′与OC共线,
所以矩形O′A′B′C′与矩形OABC是
位似图形,点O是它们的位似中心.
新知探究
新知探究
探究三:如图,已知△OAB的顶点O是坐标原点,顶点A,B的坐标分别为(-1,2),(-3,0). 把△OAB
各个顶点的横、纵坐标都扩大到
原来的3倍,得到点O′,A′,B′,
连接点O′A′,O′B′,A′B′,
△O′A′B′与△OAB是位似图形吗?
如果是,位似中心是哪个点?
x
y
O
2
-2
2
-2
A
B
6
-4
-6
A'
B'
4
-8
由= =3,∠O=∠O′,知△O′A′B′∽△OAB,相似比为3.
由OA两点的坐标可知,经过点O,A的直线为y=-2x.
由于点A′的坐标(-3, 6)适合上式,
故点A′在直线OA上.
所以△O′A′B′与△OAB的对应
顶点所在的直线都经过同一点O.
又对应边A′B′∥AB,O′A′与OA
共线,O′B′与OB共线,
所以△O′A′B′与△OAB是位似图形,点O是它们的位似中心.
x
y
O
2
-2
2
-2
A
B
6
-4
-6
A'
B'
4
-8
新知探究
新知探究
探究四:由探究一、二、三你能得出什么结论?
如果多边形有一个顶点在坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
上面得到的结论还能推广吗?如果能,说明你推广后的结论.
提示:要将上述结论推广,可适当降低命题的条件(如去掉“有一个顶点在坐标原点”的条件,再去掉“有一条边在x轴上”的条件).通过举例,画出图形,讨论上面的结论是否依然成立.
新知探究
x
y
O
2
4
-2
2
4
-2
-4
A
B
6
-6
6
如图, 在平面直角坐标系中, 四边形ABCD的顶点坐标分别为A(2,1), B(4,3), C(3,5), D(-1,3),将点A, B, C, D的横坐标、纵坐标都乘,分别得到A′ , B′ , C′ , D′ ,四边形A′B′C′D′与四边形ABCD位似吗?
如果位似,指出位似中心和相似比.
C
D
新知探究
x
y
O
2
4
-2
2
4
-2
-4
A
B
6
-6
6
C
D
坐标都乘后,得新四边形的四个顶点的坐标分别是___________________.
如图,四边形A′B′C′D′的边长为四边形ABCD的边长的___,对应点的连线都过点___.且对应边______.
(1,), (2,), (,), (-,)
O
A'
C'
B'
D'
所以四边形A′B′C′D′与四边形ABCD位似,位似中心为点O, 相似比为.
新知探究
平行
新知探究
所以,上面得到的结论还能推广,推广后的结论如下:
在平面直角坐标系中,将一个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
此结论可以称为位似图形与坐标的性质.
例题讲解
【例1】如图, 四边形OABC的顶点坐标分别为 (0,0),(2,0),(4,4),(-2,2).
(1)如果四边形O′A′B′C′与四边形OABC位似,位似中心是原点,其面积等于四边形OABC面积的倍,分别写出点A′,B′,C′的坐标.
x
y
O
2
4
-2
-4
2
4
-2
-4
A
C
B
-6
6
6
(2)画出四边形O′A′B′C′.
解:(1)由四边形O′A′B′C′与四边形OABC的面积比为,所以它们的相似比为.
将点A,B,C的坐标分别扩大到
原来的,得到A′(3,0),B′(6,6),
C′(-3,3).
(2)顺次连接O′,A′,B′,C′ ,
四边形O′A′B′C′就是要画的四边形.
例题讲解
x
y
O
2
4
-2
-4
2
4
-2
-4
A
C
B
-6
6
6
A'
C'
B'
随堂练习
1.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4) B.(-1,-2)
C. (-2,-4) D.(-2,-1)
C
随堂练习
2.如图,已知,.
(1)作出与关于轴对称的,
并写出的坐标.
(2)以原点为位似中心,在原点的另一
侧,画出,使与
位似,且.
-8 -6 -4 -2 2 4
2
-2
-4
解:
(1)
作出如图.
(2)
,
即,
画出如图.
同理,得,
-8 -6 -4 -2 2 4
2
-2
-4
-6
课堂小结
位似图形与坐标
性质
在坐标系中画位似图
在平面直角坐标系中,将一个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
首先把原图形的各点的横、纵坐标都乘相似比k或乘-k,然后描点连线即可.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
