青岛版数学九年级上册1.4.2图形的位似 教案(表格式)
文档属性
| 名称 | 青岛版数学九年级上册1.4.2图形的位似 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 313.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 18:50:49 | ||
图片预览

文档简介
2023—2024学年第 一 学期教案
课 题 第 一 单元第 四 课《 图形的位似 》 总(2)课时
主备人 使用人 授课 日期 年 月 日
背景 分析 基于学生已经学过相似、位似等有关知识,并能将某一简单图形按一定比例放大或缩小,本节课将多边形放到直角坐标系中,探讨通过直角坐标系,如何寻找它关于原点O的位似图形并确定相似比,如何将一个多边形放大或缩小.同时,也要探讨在直角坐标系中,给出相似比,如何确定一个已知多边形关于原点O的位似图形
学习 目标 1.理解位似图形的坐标变换规律. 2.能熟练在坐标系中根据坐标的变化规律作出位似图形.
学习 重点 理解位似图形的坐标变换规律.
教学 难点 能熟练在坐标系中根据坐标的变化规律作出位似图形
教学 准备 课件,尺子.
教学 评价 正文(宋体小四) 行距(16磅)
教与学活动过程 个性修改
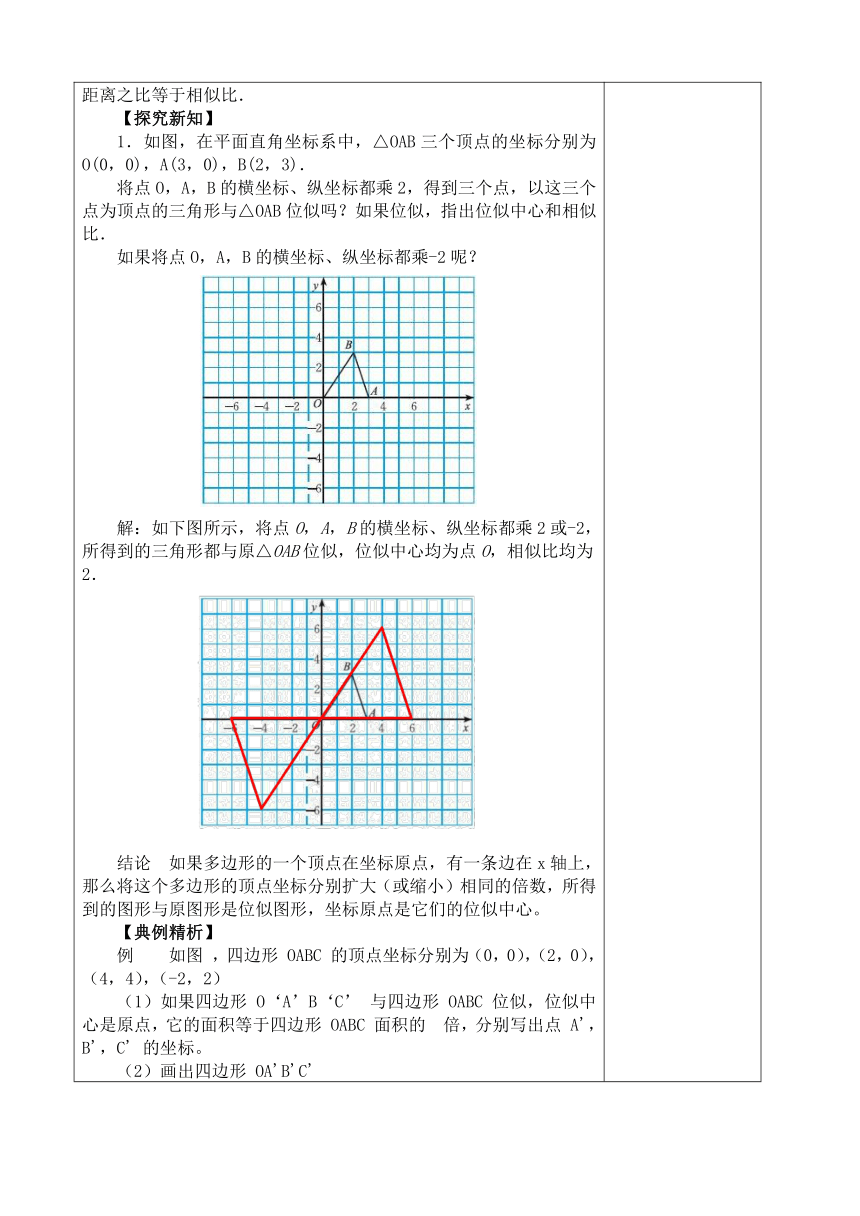
【复习引入】 1.位似图形的概念 如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似图形形.这个点叫做位似中心. 2.位似图形的性质 (1)位似图形的对应顶点的连线经过位似中心; (2)位似图形的对应边互相平行(或在同一条直线上); (3)位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于相似比. 【探究新知】 1.如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(3,0),B(2,3). 将点O,A,B的横坐标、纵坐标都乘2,得到三个点,以这三个点为顶点的三角形与△OAB位似吗?如果位似,指出位似中心和相似比. 如果将点O,A,B的横坐标、纵坐标都乘-2呢? 解:如下图所示,将点O,A,B的横坐标、纵坐标都乘2或-2,所得到的三角形都与原△OAB位似,位似中心均为点O,相似比均为2. 结论 如果多边形的一个顶点在坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心。 【典例精析】 例 如图 ,四边形 OABC 的顶点坐标分别为(0,0),(2,0),(4,4),(-2,2) (1)如果四边形 O‘A’B‘C’ 与四边形 OABC 位似,位似中心是原点,它的面积等于四边形 OABC 面积的 倍,分别写出点 A',B',C' 的坐标。 (2)画出四边形 OA'B'C' 【课堂练习】 1.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E'的坐标是( ). A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1) 2.如图,已知点E(-4,2),点F(-1,-1),以点O为位似中心,相似比为1︰2,把△EFO缩小,则点E的对应点的坐标是( ). A.(-2,1) B.(2,-1)或(-2,-1) C.(2,-1) D.(-2,1)或(2,-1) 3.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1︰.若点A的坐标为(0,1),则点E的坐标是________. 【课堂小结】 在平面直角坐标系中,如果一个多边形有一个顶点是坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大或缩小 相同的倍数,所得图形与原图形是位似图形。扩大或缩小的这个倍数就是位似图形与原图形的相似比。
课后 反思 正文(宋体小四) 行距(16磅)
课 题 第 一 单元第 四 课《 图形的位似 》 总(2)课时
主备人 使用人 授课 日期 年 月 日
背景 分析 基于学生已经学过相似、位似等有关知识,并能将某一简单图形按一定比例放大或缩小,本节课将多边形放到直角坐标系中,探讨通过直角坐标系,如何寻找它关于原点O的位似图形并确定相似比,如何将一个多边形放大或缩小.同时,也要探讨在直角坐标系中,给出相似比,如何确定一个已知多边形关于原点O的位似图形
学习 目标 1.理解位似图形的坐标变换规律. 2.能熟练在坐标系中根据坐标的变化规律作出位似图形.
学习 重点 理解位似图形的坐标变换规律.
教学 难点 能熟练在坐标系中根据坐标的变化规律作出位似图形
教学 准备 课件,尺子.
教学 评价 正文(宋体小四) 行距(16磅)
教与学活动过程 个性修改
【复习引入】 1.位似图形的概念 如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似图形形.这个点叫做位似中心. 2.位似图形的性质 (1)位似图形的对应顶点的连线经过位似中心; (2)位似图形的对应边互相平行(或在同一条直线上); (3)位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于相似比. 【探究新知】 1.如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(3,0),B(2,3). 将点O,A,B的横坐标、纵坐标都乘2,得到三个点,以这三个点为顶点的三角形与△OAB位似吗?如果位似,指出位似中心和相似比. 如果将点O,A,B的横坐标、纵坐标都乘-2呢? 解:如下图所示,将点O,A,B的横坐标、纵坐标都乘2或-2,所得到的三角形都与原△OAB位似,位似中心均为点O,相似比均为2. 结论 如果多边形的一个顶点在坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心。 【典例精析】 例 如图 ,四边形 OABC 的顶点坐标分别为(0,0),(2,0),(4,4),(-2,2) (1)如果四边形 O‘A’B‘C’ 与四边形 OABC 位似,位似中心是原点,它的面积等于四边形 OABC 面积的 倍,分别写出点 A',B',C' 的坐标。 (2)画出四边形 OA'B'C' 【课堂练习】 1.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E'的坐标是( ). A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1) 2.如图,已知点E(-4,2),点F(-1,-1),以点O为位似中心,相似比为1︰2,把△EFO缩小,则点E的对应点的坐标是( ). A.(-2,1) B.(2,-1)或(-2,-1) C.(2,-1) D.(-2,1)或(2,-1) 3.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1︰.若点A的坐标为(0,1),则点E的坐标是________. 【课堂小结】 在平面直角坐标系中,如果一个多边形有一个顶点是坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大或缩小 相同的倍数,所得图形与原图形是位似图形。扩大或缩小的这个倍数就是位似图形与原图形的相似比。
课后 反思 正文(宋体小四) 行距(16磅)
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
