2023年辽宁省阜新市数学中考真题(pdf、无答案)
文档属性
| 名称 | 2023年辽宁省阜新市数学中考真题(pdf、无答案) |

|
|
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-24 00:00:00 | ||
图片预览



文档简介
2023 年阜新市初中毕业生学业考试
数 学 试 卷
考试时间 120 分钟 试卷满分 120 分
各位同学请注意:务必将试题答案写在答题卡对应的位置上,否则不得分.千万记住哦!
一、选择题(本题共 10 个小题,每小题 3 分,共 30 分.在每一个小题给出的四个选项
中,只有一个是正确的)
1. 2的相反数是
1 1
A. 2 B. C. D.2
2 2
2.如图所示的几何体是由 5 个大小相同的立方块搭成的,它的左视图是
A B C D
(第 2 题)
3.在下列计算中,正确的是
. 1 3A 5 +( 6)= 1 B. = 2 C.3 ×( 2)= 6 D.sin 30° =
2 3
4.某中学甲、乙两支国旗护卫队的队员身高(单位:cm)数据如下:
甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,177,176,178,175,177,181,180,181.
若要判断哪支护卫队队员身高更为整齐,应该比较两组数据的
A.平均数 B.众数 C.中位数 D.方差
5.某中学举办“传承红色精神,讲好阜新故事”演讲比赛,共设置“海州矿精神”、“三沟
精神”、“治沙精神”三个主题,每位选手随机选取一个主题参赛.如果小明和小宇都参
加比赛,他们同时选中主题为“海州矿精神”的概率是
1 1 1 1
A. B. C. D.
2 3 6 9
数学试卷 第 1 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
6.不等式 x + 8 < 4x 1 的解集是
1
A.x < 3 B.x > 3 C.x < 3 D.x >
3
7.如图,A,B,C 是⊙O 上的三点,若∠AOC = 90°,∠ACB = 25°,则∠BOC 的度数是
A.20°
B.25°
C.40°
D.50° (第 7 题)
8.近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商
纷纷开展降价促销活动.某款燃油汽车今年 3 月份售价为 23 万元,5 月份售价为 16 万元.
设该款汽车这两月售价的月均下降率是 x,则所列方程正确的是
2 2
A.16 1 + x = 23 B.23 1 x = 16
. 2 C 23 23 1 x = 16 D.23 1 2x = 16
.如图,二次函数 2 9 y = ax + bx + c 的图象与 x 轴的一个交点为(3,0),对称轴是直线
x = 1,下列结论正确的是
A.abc < 0 B.2a + b = 0
2
C.4ac > b D.点( 2,0)在函数图象上
(第 9 题) (第 10 题)
10.如图,四边形 OABC1 是正方形,曲线 C1C2C3C4C5 叫做“正方形的渐开线”,其
中 , , , , 的圆心依次按 O,A,B,C1 循环.当 OA = 1 时,点
C2 023的坐标是
A.( 1, 2 022) B.( 2 023,1) C.( 1, 2 023) D.(2 022,0)
数学试卷 第 2 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
二、填空题(本题共 6 个小题,每小题 3 分,共 18 分)
0
11.计算: + 2 = ________.
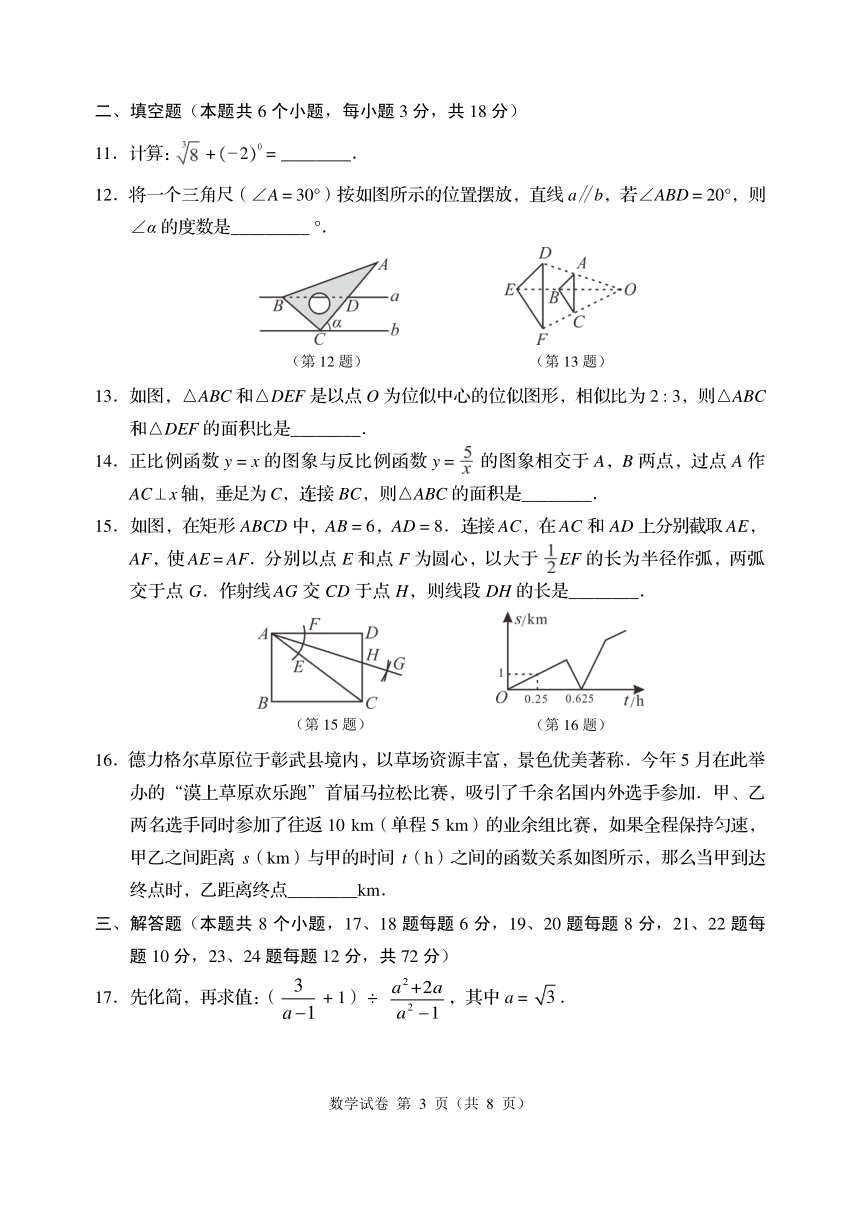
12.将一个三角尺(∠A = 30°)按如图所示的位置摆放,直线 a∥b,若∠ABD = 20°,则
∠α的度数是_________ °.
(第 12 题) (第 13 题)
13.如图,△ABC 和△DEF 是以点 O 为位似中心的位似图形,相似比为 2 : 3,则△ABC
和△DEF 的面积比是________.
14.正比例函数 y = x 的图象与反比例函数 y = 的图象相交于 A,B 两点,过点 A 作
AC⊥x 轴,垂足为C,连接 BC,则△ABC 的面积是________.
15.如图,在矩形 ABCD 中,AB = 6,AD = 8.连接 AC,在 AC 和 AD 上分别截取 AE,
AF,使 AE = AF.分别以点 E 和点 F 为圆心,以大于 EF 的长为半径作弧,两弧
交于点 G.作射线 AG 交 CD 于点 H,则线段 DH 的长是________.
(第 15 题) (第 16 题)
16.德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年 5 月在此举
办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加.甲、乙
两名选手同时参加了往返 10 km(单程 5 km)的业余组比赛,如果全程保持匀速,
甲乙之间距离 s(km)与甲的时间 t(h)之间的函数关系如图所示,那么当甲到达
终点时,乙距离终点________km.
三、解答题(本题共 8 个小题,17、18 题每题 6 分,19、20 题每题 8 分,21、22 题每
题 10 分,23、24 题每题 12 分,共 72 分)
3 a2先化简,再求值:( )÷ +2a17. + 1 ,其中 a = 3 .
a 1 a2 1
数学试卷 第 3 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
18.某中学数学兴趣小组的同学们,对函数 y = a | x b | + c(a,b,c 是常数,a ≠ 0)
的性质进行了初步探究,部分过程如下,请你将其补充完整.
(1)当 a = 1,b = c = 0 时,即 y = | x |.当 x ≥ 0 时,函数化简为 y = x;当 x < 0 时,
函数化简为 y = ________;
(2)当 a = 2,b = 1,c = 0 时,即 y = 2 | x 1 |.
①该函数自变量 x 和函数值 y 的若干组对应值如下表:
x … 2 1 0 1 2 3 4 …
y … 6 m 2 0 2 4 6 …
其中 m = ________;
②在图 1 的平面直角坐标系内画出函数 y = 2 | x 1 | 的图象;
图 1 图 2
(第 18 题)
(3)当 a = 2,b = 1,c = 2 时,即 y = 2 | x 1 | + 2.
①当 x ≥ 1 时,函数化简为 y = ________;
②在图 2 的平面直角坐标系内画出函数 y = 2 | x 1 | + 2 的图象;
(4)请写出函数 y = a | x b | + c(a,b,c 是常数,a ≠ 0)的一条性质:_______.
(若所列性质多于一条,则仅以第一条为准)
数学试卷 第 4 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
19.如图,AB 是⊙O 的直径,点 C,D 是⊙O 上 AB 异侧的两点,DE⊥CB,交 CB 的
延长线于点 E,且 BD 平分∠ABE.
(1)求证:DE 是⊙O 的切线;
(2)若∠ABC = 60°,AB = 4,求图中阴影部分的面积.
(第 19 题)
20.端午节是中华民族的传统节日,节日里吃粽子是传统习俗.为了了解附近居民对
A(肉粽子),B(蛋黄粽子),C(红枣粽子),D(葡萄干粽子)四种口味粽子的喜
爱情况,某商场随机抽取了某小区的部分居民进行问卷调查(每人只能选一种口味),
幵将调查结果绘制成如下两幅不完整的统计图.
(第 20 题)
请根据图中提供的信息,解答下列问题:
(1)参加此次问卷调查的居民共有________人;
(2)通过计算将条形统计图补充完整;
(3)若该小区共有 2 000 名居民,请估计喜爱 A(肉粽子)的居民约有多少人?
数学试卷 第 5 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
21.如图,小颖家所在居民楼高 AB 为 46 m,从楼顶 A 处测得另一座大厦顶部 C 的
仰角 α是 45°,而大厦底部 D 的俯角 β是 37°.
(1)求两楼之间的距离 BD;
(2)求大厦的高度 CD.
(结果精确到 0.1 m,参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
(第 21 题)
22.为了进一步丰富校园文体活动,某中学准备一次性购买若干个足球和排球,用 480 元
购买足球的数量和用 390 元购买排球的数量相同,已知足球的单价比排球的单价
多 15 元.
(1)求足球和排球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和排球共 100 个,但要求其总费用不超
过 7 550 元,那么学校最多可以购买多少个足球?
数学试卷 第 6 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
23.如图,在正方形 ABCD 中,线段 CD 绕点 C 逆时针旋转到 CE,旋转角为 α,点 F
在直线 DE 上,且 AD = AF,连接 BF.
(1)如图 1,当 0° < α < 90° 时,
①求∠BAF 的大小(用含 α的式子表示);
②求证:EF = 2 BF;
(2)如图 2,取线段 EF 的中点 G,连接 AG,已知 AB = 2,请直接写出在线段
CE 旋转过程中(0° < α < 360°)△ADG 面积的最大值.
图 1 图 2
(第 23 题)
数学试卷 第 7 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
24.如图,在平面直角坐标系中,二次函数 2 y = x + bx + c 的图象与 x 轴交于点
A( 3,0)和 B(1,0),与 y 轴交于点 C.
(1)求这个二次函数的表达式;
(2)如图 1,二次函数图象的对称轴与直线 AC:y = x + 3 交于点 D,若 M 是直线
AC 上方抛物线上的一个动点,求△MCD 面积的最大值;
(3)如图 2,P 是直线 AC 上的一个动点,过点 P 的直线 l 与 BC 平行,则在直线 l 上
是否存在点 Q,使点 B 与点 P 关于直线 CQ 对称?若存在,请直接写出点 Q 的
坐标;若不存在,请说明理由.
图 1 图 2
(第 24 题)
数学试卷 第 8 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
数 学 试 卷
考试时间 120 分钟 试卷满分 120 分
各位同学请注意:务必将试题答案写在答题卡对应的位置上,否则不得分.千万记住哦!
一、选择题(本题共 10 个小题,每小题 3 分,共 30 分.在每一个小题给出的四个选项
中,只有一个是正确的)
1. 2的相反数是
1 1
A. 2 B. C. D.2
2 2
2.如图所示的几何体是由 5 个大小相同的立方块搭成的,它的左视图是
A B C D
(第 2 题)
3.在下列计算中,正确的是
. 1 3A 5 +( 6)= 1 B. = 2 C.3 ×( 2)= 6 D.sin 30° =
2 3
4.某中学甲、乙两支国旗护卫队的队员身高(单位:cm)数据如下:
甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,177,176,178,175,177,181,180,181.
若要判断哪支护卫队队员身高更为整齐,应该比较两组数据的
A.平均数 B.众数 C.中位数 D.方差
5.某中学举办“传承红色精神,讲好阜新故事”演讲比赛,共设置“海州矿精神”、“三沟
精神”、“治沙精神”三个主题,每位选手随机选取一个主题参赛.如果小明和小宇都参
加比赛,他们同时选中主题为“海州矿精神”的概率是
1 1 1 1
A. B. C. D.
2 3 6 9
数学试卷 第 1 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
6.不等式 x + 8 < 4x 1 的解集是
1
A.x < 3 B.x > 3 C.x < 3 D.x >
3
7.如图,A,B,C 是⊙O 上的三点,若∠AOC = 90°,∠ACB = 25°,则∠BOC 的度数是
A.20°
B.25°
C.40°
D.50° (第 7 题)
8.近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商
纷纷开展降价促销活动.某款燃油汽车今年 3 月份售价为 23 万元,5 月份售价为 16 万元.
设该款汽车这两月售价的月均下降率是 x,则所列方程正确的是
2 2
A.16 1 + x = 23 B.23 1 x = 16
. 2 C 23 23 1 x = 16 D.23 1 2x = 16
.如图,二次函数 2 9 y = ax + bx + c 的图象与 x 轴的一个交点为(3,0),对称轴是直线
x = 1,下列结论正确的是
A.abc < 0 B.2a + b = 0
2
C.4ac > b D.点( 2,0)在函数图象上
(第 9 题) (第 10 题)
10.如图,四边形 OABC1 是正方形,曲线 C1C2C3C4C5 叫做“正方形的渐开线”,其
中 , , , , 的圆心依次按 O,A,B,C1 循环.当 OA = 1 时,点
C2 023的坐标是
A.( 1, 2 022) B.( 2 023,1) C.( 1, 2 023) D.(2 022,0)
数学试卷 第 2 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
二、填空题(本题共 6 个小题,每小题 3 分,共 18 分)
0
11.计算: + 2 = ________.
12.将一个三角尺(∠A = 30°)按如图所示的位置摆放,直线 a∥b,若∠ABD = 20°,则
∠α的度数是_________ °.
(第 12 题) (第 13 题)
13.如图,△ABC 和△DEF 是以点 O 为位似中心的位似图形,相似比为 2 : 3,则△ABC
和△DEF 的面积比是________.
14.正比例函数 y = x 的图象与反比例函数 y = 的图象相交于 A,B 两点,过点 A 作
AC⊥x 轴,垂足为C,连接 BC,则△ABC 的面积是________.
15.如图,在矩形 ABCD 中,AB = 6,AD = 8.连接 AC,在 AC 和 AD 上分别截取 AE,
AF,使 AE = AF.分别以点 E 和点 F 为圆心,以大于 EF 的长为半径作弧,两弧
交于点 G.作射线 AG 交 CD 于点 H,则线段 DH 的长是________.
(第 15 题) (第 16 题)
16.德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年 5 月在此举
办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加.甲、乙
两名选手同时参加了往返 10 km(单程 5 km)的业余组比赛,如果全程保持匀速,
甲乙之间距离 s(km)与甲的时间 t(h)之间的函数关系如图所示,那么当甲到达
终点时,乙距离终点________km.
三、解答题(本题共 8 个小题,17、18 题每题 6 分,19、20 题每题 8 分,21、22 题每
题 10 分,23、24 题每题 12 分,共 72 分)
3 a2先化简,再求值:( )÷ +2a17. + 1 ,其中 a = 3 .
a 1 a2 1
数学试卷 第 3 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
18.某中学数学兴趣小组的同学们,对函数 y = a | x b | + c(a,b,c 是常数,a ≠ 0)
的性质进行了初步探究,部分过程如下,请你将其补充完整.
(1)当 a = 1,b = c = 0 时,即 y = | x |.当 x ≥ 0 时,函数化简为 y = x;当 x < 0 时,
函数化简为 y = ________;
(2)当 a = 2,b = 1,c = 0 时,即 y = 2 | x 1 |.
①该函数自变量 x 和函数值 y 的若干组对应值如下表:
x … 2 1 0 1 2 3 4 …
y … 6 m 2 0 2 4 6 …
其中 m = ________;
②在图 1 的平面直角坐标系内画出函数 y = 2 | x 1 | 的图象;
图 1 图 2
(第 18 题)
(3)当 a = 2,b = 1,c = 2 时,即 y = 2 | x 1 | + 2.
①当 x ≥ 1 时,函数化简为 y = ________;
②在图 2 的平面直角坐标系内画出函数 y = 2 | x 1 | + 2 的图象;
(4)请写出函数 y = a | x b | + c(a,b,c 是常数,a ≠ 0)的一条性质:_______.
(若所列性质多于一条,则仅以第一条为准)
数学试卷 第 4 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
19.如图,AB 是⊙O 的直径,点 C,D 是⊙O 上 AB 异侧的两点,DE⊥CB,交 CB 的
延长线于点 E,且 BD 平分∠ABE.
(1)求证:DE 是⊙O 的切线;
(2)若∠ABC = 60°,AB = 4,求图中阴影部分的面积.
(第 19 题)
20.端午节是中华民族的传统节日,节日里吃粽子是传统习俗.为了了解附近居民对
A(肉粽子),B(蛋黄粽子),C(红枣粽子),D(葡萄干粽子)四种口味粽子的喜
爱情况,某商场随机抽取了某小区的部分居民进行问卷调查(每人只能选一种口味),
幵将调查结果绘制成如下两幅不完整的统计图.
(第 20 题)
请根据图中提供的信息,解答下列问题:
(1)参加此次问卷调查的居民共有________人;
(2)通过计算将条形统计图补充完整;
(3)若该小区共有 2 000 名居民,请估计喜爱 A(肉粽子)的居民约有多少人?
数学试卷 第 5 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
21.如图,小颖家所在居民楼高 AB 为 46 m,从楼顶 A 处测得另一座大厦顶部 C 的
仰角 α是 45°,而大厦底部 D 的俯角 β是 37°.
(1)求两楼之间的距离 BD;
(2)求大厦的高度 CD.
(结果精确到 0.1 m,参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
(第 21 题)
22.为了进一步丰富校园文体活动,某中学准备一次性购买若干个足球和排球,用 480 元
购买足球的数量和用 390 元购买排球的数量相同,已知足球的单价比排球的单价
多 15 元.
(1)求足球和排球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和排球共 100 个,但要求其总费用不超
过 7 550 元,那么学校最多可以购买多少个足球?
数学试卷 第 6 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
23.如图,在正方形 ABCD 中,线段 CD 绕点 C 逆时针旋转到 CE,旋转角为 α,点 F
在直线 DE 上,且 AD = AF,连接 BF.
(1)如图 1,当 0° < α < 90° 时,
①求∠BAF 的大小(用含 α的式子表示);
②求证:EF = 2 BF;
(2)如图 2,取线段 EF 的中点 G,连接 AG,已知 AB = 2,请直接写出在线段
CE 旋转过程中(0° < α < 360°)△ADG 面积的最大值.
图 1 图 2
(第 23 题)
数学试卷 第 7 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
24.如图,在平面直角坐标系中,二次函数 2 y = x + bx + c 的图象与 x 轴交于点
A( 3,0)和 B(1,0),与 y 轴交于点 C.
(1)求这个二次函数的表达式;
(2)如图 1,二次函数图象的对称轴与直线 AC:y = x + 3 交于点 D,若 M 是直线
AC 上方抛物线上的一个动点,求△MCD 面积的最大值;
(3)如图 2,P 是直线 AC 上的一个动点,过点 P 的直线 l 与 BC 平行,则在直线 l 上
是否存在点 Q,使点 B 与点 P 关于直线 CQ 对称?若存在,请直接写出点 Q 的
坐标;若不存在,请说明理由.
图 1 图 2
(第 24 题)
数学试卷 第 8 页(共 8 页)
{#{QQABCYSAggCoABIAARhCAQXQCkMQkBAACAgGABAEsAABSQNABAA=}#}
同课章节目录
